Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 28

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Рассуждая так же, выполни деление с остатком.
Ответ:17 : 4 17 не делится на 4 без остатка. Вспомним, какое самое большое число до 17 делится на 4 без остатка. Это число 16. Найдем частное: 16 : 4 = 4 Найдем остаток: 17 – 16 = 1 17 : 4 = 4 (ост. 1)

22 : 6 22 не делится на 6 без остатка. Вспомним, какое самое большое число до 22 делится на 6 без остатка. Это число 18. Найдем частное: 18 : 6 = 3 Найдем остаток: 22 – 18 = 4 22 : 6 = 3 (ост. 4)

27 : 5
27 не делится на 5 без остатка. Вспомним, какое самое большое число до 27 делится на 5 без остатка. Это число 25.
Найдем частное: 25 : 5 = 5
Найдем остаток: 27 – 25 = 2
27 : 5 = 5 (ост. 2)

59 : 9 59 не делится на 9 без остатка. Вспомним, какое самое большое число до 59 делится на 9 без остатка. Это число 54. Найдем частное: 54 : 9 = 6 Найдем остаток: 59 – 54 = 5 59 : 9 = 6 (ост. 5)

27 : 7 27 не делится на 7 без остатка. Вспомним, какое самое большое число до 27 делится на 7 без остатка. Это число 21. Найдем частное: 21 : 7 = 3 Найдем остаток: 27 – 21 = 6 27 : 7 = 3 (ост. 6)

1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Выполним вычисления.
Выполним деление в столбик.
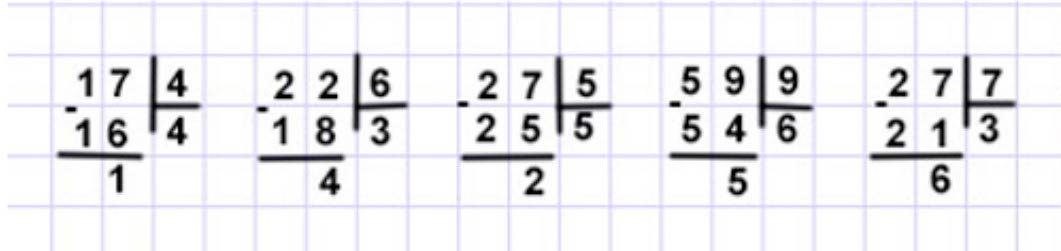
Рассуждаем.
17 : 4 = 4 (ост. 1)
17 не делится на 4 без остатка. Вспомним, какое самое большое число до 17 делится на 4 без остатка. Это 16.
Найдём частное: 16 : 4 = 4.
Найдём остаток: 17 - 16 = 1.
22 : 6 = 3 (ост. 4)
22 не делится на 6 без остатка. Вспомним, какое самое большое число до 22 делится на 6 без остатка. Это 18.
Найдем частное: 18 : 6 = 3.
Найдем остаток: 22 – 18 = 4.
27 : 5 = 5 (ост. 2)
27 не делится на 5 без остатка. Вспомним, какое самое большое число до 27 делится на 5 без остатка. Это 25.
Найдем частное: 25 : 5 = 5.
Найдем остаток: 27 – 25 = 2.
59 : 9 = 6 (ост. 5)
59 не делится на 9 без остатка. Вспомним, какое самое большое число до 59 делится на 9 без остатка. Это 54.
Найдем частное: 54 : 9 = 6.
Найдем остаток: 59 – 54 = 5.
27 : 7 = 3 (ост. 6)
27 не делится на 7 без остатка. Вспомним, какое самое большое число до 27 делится на 7 без остатка. Это 21.
Найдем частное: 21 : 7 = 3.
Найдем остаток: 27 – 21 = 6.
Делаем проверку.
17 : 4 = 4 (ост. 1)
Проверка:
1) 1 < 4 – остаток меньше делителя.
2) 4 ∙ 4 = 16 – неполное делимое.
3) 16 + 1 = 17 – делимое.
17 = 17 – деление выполнено верно.
22 : 6 = 3 (ост. 4)
Проверка:
1) 4 < 6 – остаток меньше делителя.
2) 6 ∙ 3 = 18 – неполное делимое.
3) 18 + 4 = 22 – делимое.
22 = 22 – деление выполнено верно.
27 : 5 = 5 (ост. 2)
Проверка:
1) 2 < 5 – остаток меньше делителя.
2) 5 ∙ 5 = 25 – неполное делимое.
3) 25 + 2 = 27 – делимое.
27 = 27 – деление выполнено верно.
59 : 9 = 6 (ост. 5)
Проверка:
1) 5 < 9 – остаток меньше делителя.
2) 9 ∙ 6 = 54 – неполное делимое.
3) 54 + 5 = 59 – делимое.
59 = 59 – деление выполнено верно.
27 : 7 = 3 (ост. 6)
Проверка:
1) 6 < 7 – остаток меньше делителя.
2) 7 ∙ 3 = 21 – неполное делимое.
3) 21 + 6 = 27 – делимое.
27 = 27 – деление выполнено верно.
Номер 2.
Брат собрал 18 стаканов клюквы, а сестра – 6. Чтобы сварить варенье из этой клюквы, мама брала на каждый стакан ягод 2 стакана сахара. Сколько стаканов сахара ей потребовалось?
Ответ:Брат –18 ст.
Сестра – 6 ст.
На 1 ст. кл. – 2 ст. сах.
1-й способ решения:
1) 18 + 6 = 24 (ст.) – клюквы было всего.
2) 2 · 24 = 48 (ст.) – сахара понадобилось.
Ответ: 48 стаканов сахара понадобилось, чтобы сварить варенье из клюквы.
2-й способ решения:
1) 18 · 2 = 36 (ст.) – сахара на 18 стаканов клюквы
2) 6 · 2 = 12 (ст.) – сахара на 6 стаканов клюквы
3) 36 + 12 = 48 (ст.) – нужно сахара
Ответ: 48 стаканов сахара.
3-й способ решения:
(18 + 6) · 2 = 24 · 2 = 48 (ст.) – нужно сахара
или
18 · 2 + 6 · 2 = 36 + 12 = 48 (ст.) – нужно сахара
Ответ: 48 стаканов сахара.
1) Помни, чтобы умножить сумму на число, можно вычислить сумму и умножить её на число.
2) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
Оформляем условие в виде таблицы.

Рассуждаем.
Узнаем, сколько всего собрали стаканов клюквы.
Общее количество клюквы состоит из количества, который собрал брат и собрала сестра.
18 + 6 = 24 (ст.) – клюквы собрали вместе.
Продолжаем рассуждение.
Мы узнали, что всего собрали 24 стакана клюквы. И также знаем, что на каждый стакан ягод мама брала 2 стакана сахара. Все стаканы одинаковы.
Значит, чтобы узнать, сколько потребовалось сахара, нужно общее количество клюквы умножить на количество сахара на 1 стакан.
24 ∙ 2 = 48 (ст.) – нужно сахара.
Записываем ответ.
Ответ: 48 стаканов сахара.
Решение выражением:
(18 + 6) ∙ 2 = 24 ∙ 2 = 48 (ст.) – нужно сахара, где 18 + 6 – общее количество сахара.
Рассуждаем.
Узнаем, сколько стаканов сахара потребуется для клюквы, которую собрал брат и которую собрала сестра отдельно.
Для каждого стакана клюквы нужно 2 стакана сахара. Значит, нужно количество собранной клюквы умножить на количество сахара на 1 стакан.
18 ∙ 2 = 36 (ст.) – сахара на 18 стаканов клюквы.
6 ∙ 2 = 12 (ст.) – сахара на 6 стаканов клюквы.
Продолжаем рассуждение.
Общее количество сахара складывается из количества сахара, который добавили в клюкву брата и клюкву сестры.
36 + 12 = 48 (ст.) – нужно сахара.
Записываем ответ.
Ответ: 48 стаканов сахара.
Решение выражением:
18 ∙ 2 + 6 ∙ 2 = 36 + 12 = 48 (ст.) – нужно сахара, где 18 ∙ 2 – добавили сахара на 18 стаканов;
6 ∙ 2 – добавили сахара на 6 стаканов.
Номер 3.
Какое самое большое число до 23 делится без остатка на 3? на 4? на 6? на 8? на 9?
Ответ:21 : 3 = 7 20 : 4 = 5 18 : 6 = 3 16 : 8 = 2 18 : 9 = 2
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Выпишем все числа до 23.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23.
Рассуждаем.
1)
Вспомним, какое самое большое число до 23 делится на 3 без остатка. Это 21.
21 : 3 = 7
2)
Вспомним, какое самое большое число до 23 делится на 4 без остатка. Это 20.
20 : 4 = 5
3)
Вспомним, какое самое большое число до 23 делится на 6 без остатка. Это 18.
18 : 6 = 3
4)
Вспомним, какое самое большое число до 23 делится на 8 без остатка. Это 16.
16 : 8 = 2
5)
Вспомним, какое самое большое число до 23 делится на 9 без остатка. Это 18.
18 : 9 = 2
Оформляем задание в тетрадь.
Самое большое число до 23 делится без остатка.
на 3 – это число 21;
на 4 – это число 20;
на 6 – это число 18;
на 8 – это число 16;
на 9 – это число 18.
Номер 4.
1) Длина одной шестой части отрезка АВ равна 15 мм. Начерти этот отрезок. 2) Длина отрезка CD 28 мм. Сколько миллиметров в одной седьмой части этого отрезка?
Ответ:

Ответ: длина отрезка составляет 90 мм.

Ответ: одна седьмая часть отрезка составляет 4 мм.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического рисунка.
.jpg)
Рассуждаем.
Общая длина АВ неизвестна, но отрезок разделили на 6 частей, и одна такая часть равна 15 мм.
Общая длина всей полоски складывается из длины каждой части. Значит, чтобы узнать, чему равна длина АВ, нужно сложить длину каждой из частей.
Но длина одной части одинаковая, поэтому сложение одинаковых слагаемых можно заменить умножением. И длину одной части нужно умножить на количество этих частей.
15 мм ∙ 6 = 90 мм = 9 см – длина отрезка АВ
Записываем ответ.
Ответ: 9 см.
Оформляем условие в виде схематического рисунка.
.jpg)
Рассуждаем.
Длина отрезка равна 28 мм. Нужно найти седьмую часть отрезка.
Седьмая часть – это одна седьмая, значит целый отрезок разделили на 7 равных частей и взяли только одну часть.
Значит, чтобы узнать, сколько составляет 1 часть, нужно общую длину отрезка разделить на количество частей.
28 мм : 7 = 4 мм – одна седьмая часть отрезка CD
Записываем ответ.
Ответ: 4 мм.
Номер 5.
С двух ульев за год получили 78 кг мёда. С одного из них получили 43 кг. На сколько килограммов мёда получили больше с одного улья, чем с другого?
Ответ:
1) 78 – 43 = 35 (кг) – мёда получили со второго улья. 2) 43 – 35 = 8 (кг) – на столько больше мёда собрали с первого улья, чем со второго. Ответ: с первого улья собрали на 8 кг больше мёда, чем со второго.
«На сколько больше», – вычисляется вычитанием.
Оформляем условие в виде краткой записи.
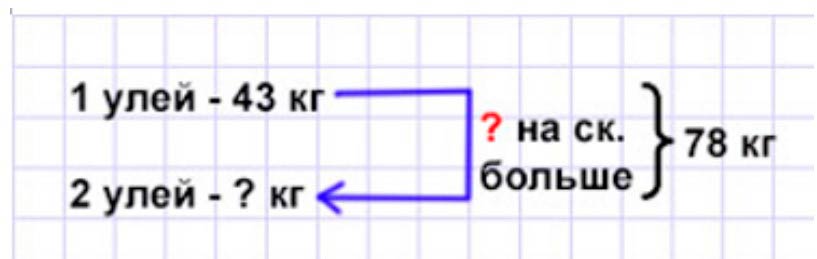
Рассуждаем.
Общее количество мёда складывается из мёда, которое собрали с первого и второго улья.
Значит, чтобы узнать, сколько мёда собрали со второго улья, нужно из общего количества мёда вычесть количество мёда, которое собрали с первого улья.
78 – 43 = 35 (кг) – со 2 улья.
Продолжаем рассуждение.
Чтобы узнать, на сколько больше мёда получили, с одного улья, чем с другого нужно из большего количества вычесть меньшее, то есть из количества мёда, которое собрали с 1 улья, вычесть, сколько собрали со 2 улья.
43 – 35 = 8 (кг) – на столько больше меда собрали с первого улья, чем со второго.
Записываем ответ.
Ответ: на 8 кг больше.
Решение выражением:
43 – (78 – 43) = 43 – 35 = 8 (кг) – на сколько больше собрали, где 78 – 43 – собрали со второго улья.
Номер 6.
Ответ:90 − (15 + 9) : 8 = 90 - 24 : 8 = 90 - 3 = 87
18 + 9 ∙ (13 − 7) = 18 + 9 ∙ 6 = 18 + 54 = 72
64 − (28 + 4) : 4 = 64 - 32 : 4 = 64 - 8 = 56
72 : 9 + 2 ∙ 7 = 8 + 14 = 22
9 ∙ 6 – 30 : 3 = 54 - 10 = 44
28 : 7 + 5 ∙ 6 = 4 + 30 = 34
7 ∙ 8 = 56
6 ∙ 9 = 54
7 ∙ 9 = 63
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним вычисления по действиям.
3 1 2
90 − (15 + 9) : 8 = 87
1) 15 + 9 = 24
2) 24 : 8 = 3
3) 90 − 3 = 87
3 2 1
18 + 9 · (13 − 7) = 72
1) 13 – 7 = 6
2) 9 ∙ 6 = 54
3) 18 + 54 = 72
3 1 2
64 – (28 + 4) : 4 = 56
1) 28 + 4 = 32
2) 32 : 4 = 8
3) 64 – 8 = 56
1 3 2
72 : 9 + 2 ∙ 7 = 22
1) 72 : 9 = 8
2) 2 ∙ 7 = 14
3) 8 + 14 = 22
1 3 2
9 ∙ 6 – 30 : 3 = 44
1) 9 ∙ 6 = 54
2) 30 : 3 = 3 дес. : 3 = 1 дес. = 10
3) 54 – 10 = 44
1 3 2
28 : 7 + 5 ∙ 6 = 34
1) 28 : 7 = 4
2) 5 ∙ 6 = 30
3) 4 + 30 = 34
Представим выражения в виде уравнения.
Чтобы найти один из множителей нужно произведение разделить на другой множитель.
х ∙ 8 = 56
х = 56 : 8
х = 7
Ответ: 7.
6 ∙ х = 54
х = 54 : 6
х = 9
Ответе: 9.
х ∙ 9 = 63
х = 63 : 9
х = 7
Ответ: 7.
Оформляем задание в тетрадь.
3 1 2
90 − (15 + 9) : 8 = 90 − 24 : 8 = 90 − 3 = 87
3 2 1
18 + 9 · (13 − 7) = 18 + 9 · 6 = 18 + 54 = 72
3 1 2
64 – (28 + 4) : 4 = 64 – 32 : 4 = 64 – 8 = 56
1 3 2
72 : 9 + 2 ∙ 7 = 8 + 14 = 22
1 3 2
9 ∙ 6 – 30 : 3 = 54 – 10 = 44
1 3 2
28 : 7 + 5 ∙ 6 = 4 + 30 = 34
7 ∙ 8 = 56
6 ∙ 9 = 54
7 ∙ 9 = 63
Номер 7.
Как из каждого числа первой строки получено записанное под ним число во второй строке?
Продолжи второй ряд чисел.
1) 2, 3, 4, 5, 6, 7, 8, 9, 10. 2) 7, 10, 13, 16, 19, 22, ..., ..., ... .
Ответ:Из каждого числа первой строки получено записанное под ним число во второй строке, путем прибавления к числам первого ряда нечетных чисел.
2 + 5 = 7
3 + 7 = 10
4 + 9 = 13
Значит, числа второго ряда будут получены так:
8 + 17 = 25
9 + 19 = 28
10 + 21 = 31
Чтобы продолжить ряд чисел, проанализируй первый и второй ряды: какие они, какие изменения происходят с числами.
Рассуждаем.
Способ 1.
Чтобы получить число из второй строки нужно к каждому числу первой строки прибавить нечетное число по возрастанию начиная с 5. То есть к первому числу прибавили 5, ко второму прибавили 7, к третьему – 9 и так далее.
Способ 2.
Или чтобы получить число из второй строки нужно число из первой строки умножить на 3 и прибавить к полученному произведению 1.
Продолжим ряд.
Способ 1.
2 + 5 = 7
3 + 7 = 10
4 + 9 = 13
5 + 11 = 16
6 + 13 = 19
7 + 15 = 22
8 + 17 = 25
9 + 19 = 28
10 + 21 = 31
Способ 2.
2 ∙ 3 + 1 = 7
3 ∙ 3 + 1 = 10
4 ∙ 3 + 1 = 13
5 ∙ 3 + 1 = 16
6 ∙ 3 + 1 = 19
7 ∙ 3 + 1 = 22
8 ∙ 3 + 1 = 25
9 ∙ 3 + 1 = 28
10 ∙ 3 + 1 = 31
Оформляем задание в тетрадь.
1) 2, 3, 4, 5, 6, 7, 8, 9, 10.
2) 7, 10, 13, 16, 19, 22, 25, 28, 31.
Задание внизу страницы
Какое самое большое число до 47 делится без остатка на 5? на 6? на 8? на 9?
Ответ:1) 45 : 5 = 9 2) 42 : 6 = 7 3) 40 : 8 = 5 4) 45 : 9 = 5
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Рассуждаем.
1)
Вспомним, какое самое большое число до 47 делится на 5 без остатка.
Это 45.
45 : 5 = 9
2)
Вспомним, какое самое большое число до 47 делится на 6 без остатка.
Это 42.
42 : 6 = 7
3)
Вспомним, какое самое большое число до 47 делится на 8 без остатка.
Это 40.
40 : 8 = 5
4)
Вспомним, какое самое большое число до 47 делится на 9 без остатка.
Это 45.
45 : 9 = 5
Оформляем задание в тетрадь.
Самое большое число до 47 делится без остатка.
на 5 – это число 45;
на 6 – это число 42;
на 8 – это число 40;
на 9 – это число 45.
Задание на полях страницы
Ребусы:


1) Вспомни как выполняется деление с остатком;
2) Вспомни названия компонентов действия сложения и деления, а также – зависимость между компонентами и результатами действий сложения и вычитания, умножения и деления.
Рассуждаем.
Вспомним, какое самое большое число более 50 но менее 60 делится на 6 без остатка. Это 56.
Найдем частное: 54 : 6 = 9
Остаток равен 2, найдем делимое: 54 + 2 = 56.
Первое число равно 6.
Второе число и третье число равно 5 и 4.
Четвертое число равно 9.
Записываем ответ.
Получим равенство:
56 : 6 = 9 (ост. 2)
.jpg)
Рассуждаем.
Найдём неполное делимое.
9 ∙ 9 = 81
Первое и второе число равно 8 и 1.
Найдем остаток: 89 – 81 = 8.
Третье число 8.
Записываем ответ.
Получим равенство:
89 : 9 = 9 (ост. 8)
.jpg)
Рассуждаем.
Так как если к числу 8 прибавить другое число получится 6 не может, поэтому 1 пойдет к десяткам.
х + 8 = 16
х = 16 – 8
х = 8
Первое число 8.
Продолжаем рассуждение.
Так как 1 пошла к десяткам, то
7 + 1 + х = 9
8 + х = 9
х = 9 – 8
х = 1
Второе число – 1.
Записываем ответ.
Получим равенство: 78 + 18 = 96
.jpg)
Рассуждаем.
Чтобы найти неизвестное слагаеоме, нужно из суммы вычесть второе слагаемое.
24 + х = 70
х = 70 – 24
х = 46
Первое число 6.
Второе число 4.
Записываем ответ.
24 + 46 = 70
.jpg)
Номер 1.
Сколько порций по 3 блина выйдет, если всего испекли 18 блинов? 19 блинов? 25 блинов?
Ответ:
1) 18 : 3 = 6 (п.) – по 3 блина. 2) 19 : 3 = 6 (ост. 1) – 6 порций и 1 блин останется. 3) 25 : 3 = 8 (ост. 1) – 8 порций и 1 блин останется.
Данная задача: вида «кол-во порций, блинов в 1 порции, всего блинов» характеризуется зависимостями между компонентами:
Кол-во порций · блинов в 1 порции = всего блинов.
Всего блинов : кол-во порций = блинов в 1 порции.
Всего блинов : блинов в 1 порции = кол-во порций.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Количество блинов в каждой порции одинаковое, значит, чтобы узнать, сколько получится порций, нужно общее количество блинов разделить на количество блинов в 1 порции.
1) 18 : 3 = 6 (п.) – из 18 блинов получится 6 полных порций.
2) 19 : 3 = 6 (ост. 1) – из 19 блинов получится 6 полных порций и 1 блин останется.
3) 25 : 3 = 8 (ост. 1) – из 20 блинов получится 18 полных порций и 1 блин останется
Записываем ответ.
Ответ: 6 порций; 6 порций и 1 блин останется; 8 порций и 1 блин останется.
Номер 2.
Какое самое большое число до 53 делится без остатка на 9? на 8? на 7?
Ответ:45 : 9 = 5 48 : 8 = 6 49 : 7 = 7
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Рассуждаем.
53 не делится на 9 без остатка. Вспомним, какое самое большое число до 53 делится на 9 без остатка. Это 45.
45 : 9 = 5
Проверяем:
53 – 45 = 8, 8 < 9, значит, всё верно.
53 не делится на 8 без остатка. Вспомним, какое самое большое число до 53 делится на 8 без остатка. Это 48.
48 : 8 = 6
Проверяем:
53 – 48 = 5, 5 < 9, значит, всё верно.
53 не делится на 7 без остатка. Вспомним, какое самое большое число до 53 делится на 7 без остатка. Это 49.
49 : 7 = 7
Проверяем:
53 – 49 = 4, 4 < 9, значит, всё верно.
Оформляем задание в тетрадь.
45 : 9 = 5
48 : 8 = 6
49 : 7 = 7
Номер 3.
Вычисли и проверь деление умножением.
Ответ:99 : 33 = 3 84 : 7 = 12
3 ∙ 33 = 99 12 ∙ 7 = 84
99 = 99 84 = 84
56 : 2 = 28 72 : 3 = 24
28 ∙ 2 = 56 24 ∙ 3 = 72
56 = 56 72 = 72
Вспомни зависимость между элементами и результатом действия умножения и деления.
Делимое : делитель = частное.
Делимое : частное = делитель.
Частное · делитель = делимое.
1 множитель · 2 множитель = произведение.
Произведение : 1 множитель = 2 множитель.
Произведение : 2 множитель = 1 множитель.
Вычисляем.
99 : 33 =
Пробуем в частном 2 и проверяем:
33 ∙ 2 = (30 + 3) ∙ 2 = 60 + 6 = 66,
66 < 99, число 2 не подходит.
Пробуем в частном 3 и проверяем:
33 ∙ 3 = (30 + 3) ∙ 3 = 90 + 9 = 99,
99 = 99, значит,
99 : 33 = 3.
Выполним деление с помощью правила деления суммы на число:
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
Представим число 84 в виде суммы 70 и 14, каждое слагаемое разделим на 7 и полученные результаты сложим.
56 : 2 = (40 + 16) : 2 = 20 + 8 = 28
Представим число 56 в виде суммы 40 и 16, каждое слагаемое разделим на 2 и полученные результаты сложим.
72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
Представим число 72 в виде суммы 60 и 12, каждое слагаемое разделим на 3 и полученные результаты сложим.
Выполняем проверку.
99 : 33 = 3
Проверка:
33 ∙ 3 = (30 + 3) ∙ 3 = 90 + 9 = 99
99 = 99
Решение выполнено верно.
84 : 7 = 12
Проверка:
12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84
84 = 84
Решение выполнено верно.
56 : 2 = 28
Проверка:
28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56
56 = 56
Решение выполнено верно.
72 : 3 = 24
Проверка:
24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72
72 = 72
Решение выполнено верно.
Оформляем задание в тетрадь
99 : 33 = 3
Проверка:
33 ∙ 3 = 99
99 = 99
84 : 7 = 12
Проверка:
12 ∙ 7 = 84
84 = 84
56 : 2 = 28
Проверка:
28 ∙ 2 = 56
56 = 56
72 : 3 = 26
Проверка:
26 ∙ 3 = 72
72 = 72
Номер 4.
В среду в библиотеке побывало 34 человека, в четверг – на 25 человек меньше, а в пятницу – в 3 раза больше, чем в четверг. Объясни, что означают выражения, и вычисли их значения:

1) «на 25 меньше», значит, из числа нужно вычесть 25.
2) «в 3 раза больше», значит, 3 раза по столько, т.е. умножить на 3.
Оформляем краткую запись.
Среда – 34 человека.
Четверг – ? человек, на 25 человек меньше, чем в среду.
Пятница – ? человек, в 3 раза больше, чем в четверг.
34 – 25 – ?
(34 – 25) ∙ 3 – ?
Рассуждаем.
Рассмотрим первое выражение.
Количество человек, которое было в среду, уменьшили на 25. Также по условию, мы знаем, что в четверг было на 25 человек меньше, чем в среду. Значит, данным выражением мы найдём, сколько человек было в библиотеке в четверг.
34 – 25 = 9 (ч.) – было в четверг.
Продолжаем рассуждение.
Рассмотрим второе выражение.
Количество человек, которое было в четверг умножили на 3, то есть увеличили в 3 раза. Также по условию, мы знаем, что в пятницу пришло в 3 раза больше человек, чем в четверг. Значит, данным выражением мы найдём, сколько человек было в библиотеке в пятницу.
(34 − 25) ∙ 3 = 9 ∙ 3 = 27 (ч.) – было в пятницу.
Оформляем задание в тетрадь.
34 – 25 = 9 (чел.) – было в четверг.
(34 − 25) ∙ 3 = 9 ∙ 3 = 27 (чел.) – было в пятницу.
Номер 5.
Сначала выпиши парами выражения с равными значениями. Найди способ себя проверь.
Ответ:4 ∙ 7 = 7 ∙ 4
4 ∙ 7 = 28
7 ∙ 4 = 28
8 ∙ 5 = 5 ∙ 8
8 ∙ 5 = 40
5 ∙ 8 = 40
3 ∙ 9 = 9 ∙ 3
3 ∙ 9 = 27
9 ∙ 3 = 27
9 ∙ 8 = 8 ∙ 9
9 ∙ 8 = 72
8 ∙ 9 = 72
5 ∙ 7 + 5 = 5 ∙ 9 – 5
5 ∙ 7 + 5 = 35 + 5 = 40
5 ∙ 9 – 5 = 45 – 5 = 40
8 ∙ 9 – 8 = 8 ∙ 7 + 8
8 ∙ 9 – 8 = 72 – 8 = 64
8 ∙ 7 + 8 = 56 + 8 = 64
3 ∙ 10 – 3 = 3 ∙ 8 + 3
3 ∙ 10 – 3 = 30 – 3 = 27
3 ∙ 8 + 3 = 24 + 3 = 27
7 ∙ 5 – 7 = 7 ∙ 3 + 7
7 ∙ 5 – 7 = 35 – 7 = 28
7 ∙ 3 + 7 = 21 + 7 = 28
Вспомни о свойствах умножения:
а · b = b · a - переместительное свойство умножения – от перестановки мест слагаемых, произведение не изменяется.
Рассуждаем.
Выпишем парами выражения с одинаковыми значениями.
4 ∙ 7 = 7 ∙ 4 – применили переместительное свойство умножения.
8 ∙ 5 = 5 ∙ 8 – применили переместительное свойство умножения.
3 ∙ 9 = 9 ∙ 3 – применили переместительное свойство умножения.
9 ∙ 8 = 8 ∙ 9 – применили переместительное свойство умножения.
5 ∙ 7 + 5 = 5 ∙ 9 – 5, так как:
5 ∙ 7 + 5 = 5 ∙ 8
5 ∙ 9 – 5 = 5 ∙ 8
8 ∙ 9 – 8 = 8 ∙ 7 + 8, так как:
8 ∙ 9 – 8 = 8 ∙ 8
8 ∙ 7 + 8 = 8 ∙ 8
3 ∙ 10 – 3 = 3 ∙ 8 + 3, так как:
3 ∙ 10 – 3 = 3 ∙ 9
3 ∙ 8 + 3 = 3 ∙ 9
7 ∙ 5 – 7 = 7 ∙ 3 + 7, так как:
7 ∙ 5 – 7 = 7 ∙ 4
7 ∙ 3 + 7 = 7 ∙ 4
Делаем проверку.
4 ∙ 7 = 7 ∙ 4
Проверка:
4 ∙ 7 = 28
7 ∙ 4 = 28
28 = 28
8 ∙ 5 = 5 ∙ 8
Проверка:
8 ∙ 5 = 40
5 ∙ 8 = 40
40 = 40
3 ∙ 9 = 9 ∙ 3
Проверка:
3 ∙ 9 = 27
9 ∙ 3 = 27
27 = 27
9 ∙ 8 = 8 ∙ 9
Проверка:
9 ∙ 8 = 72
8 ∙ 9 = 72
72 = 72
5 ∙ 7 + 5 = 5 ∙ 9 – 5
Проверка:
5 ∙ 7 + 5 = 35 + 5 = 40
5 ∙ 9 – 5 = 45 – 5 = 40
40 = 40
8 ∙ 9 – 8 = 8 ∙ 7 + 8
Проверка:
8 ∙ 9 – 8 = 72 – 8 = 64
8 ∙ 7 + 8 = 56 + 8 = 64
64 = 64
3 ∙ 10 – 3 = 3 ∙ 8 + 3
Проверка:
3 ∙ 10 – 3 = 30 – 3 = 27
3 ∙ 8 + 3 = 24 + 3 = 27
27 = 27
7 ∙ 5 – 7 = 7 ∙ 3 + 7
Проверка:
7 ∙ 5 – 7 = 35 – 7 = 28
7 ∙ 3 + 7 = 21 + 7 = 28
28 = 28
Номер 6.
Альбом для рисования и карандаш стоят 15 р. На все свои деньги Оля может купить 1 альбом или 4 карандаша. Сколько денег у Оли? Сделай вывод из условия, которое выделено, и закончи решение.
Ответ:Альбом и карандаш – 15 рублей ? – 1 альбом ИЛИ 4 карандаша Предположим, что альбом стоит 10, а карандаш 5. Тогда если Оля купит 1 альбом, то заплатит 10 рублей, а если 4 карандаша, то 20 рублей. Значит, пробуем другие цены. Допустим, что альбом стоил 11 рублей. Тогда карандаш стоит 4 рубля. На свои деньги Оля купит 1 альбом, который будет стоить 11 рублей, а если купить 4 карандаша, то потратит 16 рублей. Пробуем другие цены. Если альбом стоит 12 рублей, то карандаш – 3 рубля. Если Оля купит 1 альбом, то заплатит 12 рублей, а если 4 карандаша, то 12 рублей. Значит, у Оли было 12 рублей. Ответ: 12 рублей было у Оли всего.
Внимательно читай условия задачи, перебирай возможные варианты её решения.
Оформляем краткую запись.
Альбом + карандаш – 15 р.
1 альбом = 4 карандаша.
Сколько денег у Оли?
Рассуждаем.
Предположим, что альбом стоит 10 рублей, а карандаш – 5 рублей, тогда 5 ∙ 4 = 20 (р.) – стоимость четырёх карандашей.
10 < 20
А по условию задачи стоимость 1 альбома и 4 карандашей равны.
Значит, данный вариант не подходит.
Продолжаем рассуждение.
Предположим, что альбом стоит 11 рублей, тогда карандаш – 4 рубля, значит, 4 ∙ 4 = 16 (р.) – стоимость четырёх карандашей.
11 < 16
А по условию задачи стоимость 1 альбома и 4 карандашей равны.
Значит, данный вариант не подходит.
Продолжаем рассуждение.
Допустим, что альбом стоит 12 рублей, то карандаш – 3 рубля, значит, 3 ∙ 4 = 12 (р.) – стоимость четырёх карандашей.
12 = 12
Следовательно, данное предположение верно.
Таким образом, мы узнали, что карандаш стоит 3 рубля, а альбом 12 рублей.
У Оли 12 рублей.
Записываем ответ.
Ответ: у Оли 12 рублей.
Задание внизу страницы
На одно окно требуется 3 одинаковых стекла. Сколько окон можно застеклить, если есть 10 таких стекол? 20 стекол?
Ответ:1) 10 : 3 = 3 (ок.) и (ост. 1ст.) 2) 20 : 3 = 6 (ок.) и (ост. 2ст.) Ответ: 3 окна можно застеклить из 10 таких стёкол, 6 окон можно застеклить из 20 стёкол.
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Оформляем краткую запись.
3 стекла – 1 окно.
10 стекол – ? окон.
20 стекол – ? окон.
Рассуждаем.
На одно окно требуется 3 стекла. Чтобы узнать, сколько окон можно застеклить с помощью 10 стёкол и 20 стёкол, нужно общее количество стёкол разделить на количество стёкол, которое потребуется на одно окно.
1) 10 : 3 = 3 (ост. 1)
Если разделить 10 стёкол на группы по 3 стекла, то получим 3 такие группы и ещё останется 1 стекло.
Значит, можно застеклить 3 окна и ещё 1 стекло останется.
2) 20 : 3 = 6 (ост. 2)
Если разделить 20 стёкол на группы по 3 стекла, то получим 6 таких групп и ещё останется 2 стекла.
Значит, можно застеклить 6 окон и ещё 2 стекла останется.
Записываем ответ.
Ответ: 3 окна, 6 окон.
Задание на полях страницы
Найди лишнее выражение:
27 + 30 20 + 37 50 + 7 34 + 23 45 + 12 40 + 16
Ответ:27 + 30 = 57 20 + 37 = 57 50 + 7 = 57 34 + 23 = 57 45 + 12 = 57 40 + 16 = 56 (Лишнее выражение)
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим выражения.
27 + 30 = 57
20 + 37 = 57
50 + 7 = 57
34 + 23 = 57
45 + 12 = 57
40 + 16 = 56
Делаем вывод.
40 + 16 = 56 – лишнее, так как в остальных примерах сумма равна 57.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.