Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 20

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Объясни решение уравнений и проверку.
Ответ:
х – неизвестный делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестное делимое. Чтобы найти неизвестное делимое, нужно делитель умножить на частное. Чтобы это проверить, подставляем вместо х полученное значение.
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим первое уравнение:
76 : х = 38
х – неизвестный делитель.
Чтобы найти делитель нужно делимое разделить на частное.
Чтобы найти х нужно 76 разделить на 38, получим
х = 76 : 38
Пробуем в частном 2 и проверяем: 38 ∙ 2 = 76, 76 = 76, значит 76 : 36 = 2.
х = 2
Ответ: 2.
Рассмотрим второе уравнение:
х ∙ 7 = 84
х – неизвестный множитель.
Чтобы найти один из множителей нужно произведение разделить на другой множитель.
Чтобы найти х нужно 84 разделить на 7, получим
х = 84 : 7
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
Число 84 представим в виде суммы 70 и 14, и каждое слагаемое разделим на 7, а полученные числа сложим.
х = 12
Ответ: 12.
Рассмотрим третье уравнение:
х : 3 = 24
х – неизвестное делимое
Чтобы найти делимое нужно частное умножить на делимое.
Чтобы найти х нужно 24 умножить на 3, получим
х = 24 ∙ 3
24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72
Число 24 представим в виде суммы 20 и 4, и каждое слагаемое умножим на 3, а полученные числа сложим.
х = 72
Ответ: 72.
Делаем проверку.
Чтобы произвести проверку нужно вместо х подставить найденный множитель. Должно получиться верное равенство. Если этого не произойдёт, значит, в вычислениях допущена ошибка.
Уравнение 1: 76 : х = 38.
Проверка: вместо неизвестного х нужно подставить число 2.
76 : 2 = (60 + 16) : 2 = 30 + 8 = 38
38 = 38
Уравнение решено верно.
Уравнение 2: х ∙ 7 = 84.
Проверка: вместо неизвестного х нужно подставить число 12.
12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84
84 = 84
Уравнение решено верно.
Уравнение 3: х : 3 = 24.
Проверка: вместо неизвестного х нужно подставить число 72.
72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
24 = 24
Уравнение решено верно.
Оформляем задание в тетрадь.
76 : х = 38
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 76 : 38
х = 2
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
76 : 2 = 38
38 = 38
х ∙ 7 = 84
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 84: 7
х = 12
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
12 ∙ 7 = 84
84 = 84
х : 3 = 24
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
х = 24 ∙ 3
х = 72
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
72 : 3 = 24
24 = 24
Номер 1.
Реши уравнения с объяснением.
Ответ:
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим первое уравнение.
18 ∙ х = 54
18 – первый множитель
х – второй множитель
54 – произведение
Чтобы найти неизвестный множитель нужно произведение разделить на другой множитель.
Чтобы найти х нужно 54 разделить на 18.
х = 54 : 18
х = 3
Ответ: 3.
Рассмотрим второе уравнение.
х : 16 = 3
х –делимое
16 – делитель
3 – частное
Чтобы найти делимое нужно делитель умножить на частное.
Чтобы найти х нужно 16 умножить на 3.
х = 16 ∙ 3
х = 48
Ответ: 48.
Рассмотрим третье уравнение.
57 : х = 3
57 – делимое
х – делитель
3 – частное
Чтобы найти делитель нужно делимое разделить на частное.
Чтобы найти х нужно 57 разделить на 3.
х = 57 : 3
х = 19
Ответ: 48.
Делаем проверку.
Чтобы произвести проверку нужно вместо х подставить найденный множитель. Должно получиться верное равенство. Если этого не произойдёт, значит, в вычислениях допущена ошибка.
Уравнение 1: 18 ∙ х = 54
Проверка: вместо неизвестного х подставим число 3.
18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54
54 = 54
Уравнение решено верно.
Уравнение 2: х : 16 = 3
Проверка: вместо неизвестного х подставим число 48.
48 : 16 = 3
3 = 3
Уравнение решено верно.
Уравнение 3: 57 : х = 3
Проверка: вместо неизвестного х подставим число 19.
57 : 19 = 3
3 = 3
Уравнение решено верно.
Оформляем задание в тетрадь.
18 ∙ х = 54
Чтобы найти неизвестный множитель нужно произведение разделить на другой множитель.
х = 54 : 18
х = 3
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
18 ∙ 3 = 54
54 = 54
х : 16 = 3
Чтобы найти делимое нужно делитель умножить на частное.
х = 16 ∙ 3
х = 48
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
48 : 16 = 3
3 = 3
57 : х = 3
Чтобы найти делитель нужно делимое разделить на частное.
х = 57 : 3
х = 19
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
57 : 19 = 3
3 = 3
Номер 2.
Закончи выводы:
1) Чтобы найти неизвестный множитель, надо ... . 2) Чтобы найти неизвестное делимое, надо ... . 3) Чтобы найти неизвестный делитель, надо ... .
Ответ:1) ... произведение поделить на известный множитель. 2) ... частное умножить на делитель. 3) ... делимое поделить на частное.
Помни о зависимости между элементами и результатом действия умножения и деления.
Рассуждаем.
Вспомним зависимость между умножением и делением:
1 множитель · 2 множитель = произведение
Произведение : 1 множитель = 2 множитель
Произведение : 2 множитель = 1 множитель
Делимое : делитель = частное
Делимое : частное = делитель
Частное · делитель = делимое
Оформляем задание в тетрадь.
Закончим выводы.
1) Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
2) Чтобы найти неизвестное делимое, надо делитель умножить на частное.
3) Чтобы найди неизвестный делитель, надо делимое разделить на частное.
Номер 3.
Ответ:

1) a · b, значит, значение a нужно умножить на b.
2) c : k, значит, значение c нужно разделить на k.
Рассуждаем.
Представим данные выражения в виде уравнений.
17 ∙ х = 51
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 51 : 17
х = 3
х ∙ 4 = 68
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 68 : 4
х = 17
16 ∙ х = 96
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 96 : 16
х = 6
64 : х = 4
Чтобы найди неизвестный делитель, надо делимое разделить на частное.
х = 64 : 4
х = 16
х : 6 = 13
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
х = 13 ∙ 6
х = 78
80 : х = 5
Чтобы найди неизвестный делитель, надо делимое разделить на частное.
х = 80 : 5
х = 16
Оформляем задание в тетрадь.
Подставим полученные значения в таблицу.
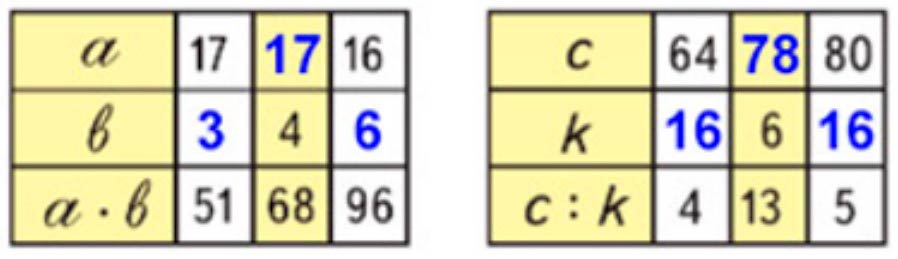
Номер 4.
В туристский поход пошли 19 человек. На каждого взяли по 2 банки мясных консервов и по 3 банки овощных. Сколько всего банок с консервами взяли?
Ответ:
Можно оформить с помощью таблицы:

1-й способ решения:
1) 2 + 3 = 5 (б.) – консервов взяли.
2) 5 · 19 = 95 (б.)
Ответ: 95 банок взяли всего.
2-й способ решения:
1) 2 · 19 = 38 (б.) – мясных консервов взяли.
2) 3 · 19 = 57 (б.) – овощных консервов взяли.
3) 38 + 57 = 95 (б.)
Ответ: 95 банок взяли всего.
3-й способ решения:
19 · (2 + 3) = 19 · 5 = 95 (б.) – всего
или
19 · 2 + 19 · 3 = 38 + 57 = 95 (б.) – всего
Ответ: 95 банок.
Данная задача: вида «на 1 человека, кол-во человек, всего банок» характеризуется зависимостями между компонентами:
На 1 человека ∙ кол-во человек = всего банок.
Всего банок : на 1 человека = кол-во человек.
Всего банок : кол-во человек = на 1 человека.
Оформляем условие в виде таблицы.

Рассуждаем.
Узнаем сколько всего банок взяли на одного человека. Общее количество банок складывается из количества мясных и овощных банок. Значит, чтобы узнать, сколько всего взяли банок на одного человека, нужно сложить количество данных банок.
2 + 3 = 5 (б.) – на 1 человека
Продолжаем рассуждение.
Мы знаем количество банок на одного человека и количество человек. Также на каждого человека количество банок одинаково. Чтобы узнать сколько всего взяли банок нужно количество человек умножить на количество банок на одного человека.
19 ∙ 5 = (10 + 9) ∙ 5 = 10 ∙ 5 + 9 ∙ 5 = 50 + 45 = 95 (б.) – всего взяли.
Записываем ответ.
Ответ: 95 банок.
Решение выражением:
(2 + 3) ∙ 19 = 95 (б.), где 2 + 3 – количество банок на одного человека.
Рассуждаем.
Для каждого человека взяли одинаковое количество мясных банок. Чтобы узнать сколько всего взяли мясных банок нужно количество банок умножить общее число человек.
19 ∙ 2 = 38 (б.) – мясные консервы.
Продолжаем рассуждение.
Для каждого человека взяли одинаковое количество овощных банок. Чтобы узнать сколько всего взяли овощных банок нужно количество банок умножить общее число человек.
19 ∙ 3 = 57 (б.) – овощные консервы.
Продолжаем рассуждение.
Общее количество банок складывается из мясных и овощных. Значит, чтобы узнать, сколько всего взяли банок, нужно сложить количества банок каждой группы.
38 + 57 = 95 (б.) – всего взяли.
Записываем ответ.
Ответ: 95 банок.
Решение выражением:
19 ∙ 2 + 19 ∙ 3 = 95 (б.), где 19 ∙ 2 – мясных банок; 19 ∙ 3 – овощных банок.
Номер 5.
Составь задачу по выражению (18 + 42) : 6.
Ответ:В ящики, каждый из которых вмещает по 6 кг разложили 18 кг мандарин и 42 кг апельсин. Сколько всего ящиков потребовалось?

1-й способ решения:
(18 + 42) : 6 = 10 (ящ.)
Ответ: 10 ящиков потребовалось всего.
2-й способ решения:
1) 18 : 6 = 3 (кор.) – для кексов
2) 42 : 6 = 7 (кор.) – для зефир
3) 3 + 7 = 10 (кор.) – всего коробок
или
18 : 6 + 42 : 6 = 3 + 7 = 10 (кор.) – всего коробок
Ответ: 10 коробок.
1) Чтобы разделить сумму на число можно вычислить сумму и разделить её на число;
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Составим задачу.
Задача: Для 6 подарков привезли 18 шоколадок и 42 конфеты. Сколько сладостей было в каждом подарке, если все коробки одинаковы?
Оформляем условие в виде таблицы.
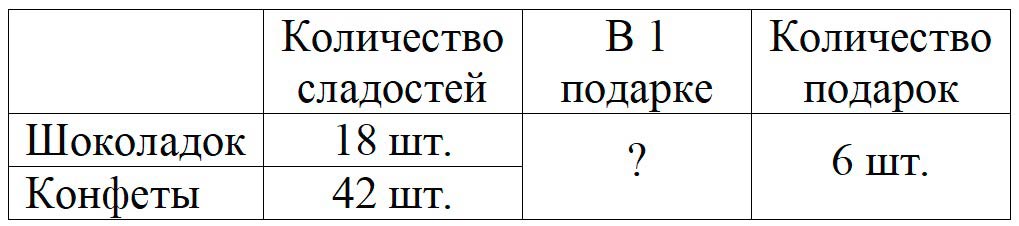
Рассуждаем.
Общее число сладостей складывается из количества шоколадок и конфет. Чтобы узнать, сколько всего сладостей привезли нужно сложить количество шоколадок и конфет.
18 + 42 = 60 (шт.) – всего сладостей.
Продолжаем рассуждение.
В каждом подарке одинаковое количество сладостей. Чтобы узнать сколько сладостей в каждом подарке нужно общее количество сладостей разделить на количество подарков.
60 : 6 = 10 (сладостей) – в каждом подарке.
Записываем ответ.
Ответ: 10 сладостей.
Решение выражением:
(18 + 42) : 6 = 60 : 6 = 10 (сл.) – в каждом подарке, где 18 + 42 – всего сладостей.
Номер 6.
(Устно.) Назови числа от 7 до 70, которые делятся на 7 без остатка.
Ответ:7, 14, 21, 28, 35, 42, 49, 56, 63, 70.
Для выполнения задания обращайся к таблице умножения и деления на 7.
Рассуждаем.
Делятся на 7, значит, являются результатом таблицы умножения и деления 7.
7 ∙ 1 = 7
7 ∙ 2 = 14
7 ∙ 3 = 21
7 ∙ 4 = 28
7 ∙ 5 = 35
7 ∙ 6 = 42
7 ∙ 7 = 49
7 ∙ 8 = 56
7 ∙ 9 = 63
7 ∙ 10 = 70
Записываем ответ.
Записываем числа от 7 до 70, которые делятся на 7.
7, 14, 21, 28, 35, 42, 49, 56, 63, 70.
Номер 7.
Ответ:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним вычисления по действиям.
1 2
28 · 3 − 57 = 27
1) 28 ∙ 3 = (20 + 8) ∙ 3 = 60 + 24 = 84
2) 84 − 57 = 27
2 1
34 + 13 · 5 = 99
1) 13 ∙ 5 = (10 + 3) ∙ 5 = 50 + 15 = 65
2) 34 + 65 = 99
2 1 3
98 – 23 ∙ 4 + 24 = 30
1) 23 ∙ 4 = (20 + 3) ∙ 4 = 80 + 12 = 92
2) 98 – 92 = 6
3) 6 + 24 = 30
1 3 2
28 ∙ 2 – 13 ∙ 4 = 4
1) 28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56
2) 13 ∙ 4 = 52
3) 56 – 52 = 4
Применим правило деления числа на сумму.
(49 + 28) : 7 = 49 : 7 + 28 : 7 = 7 + 4 = 11
Каждое слагаемое разделим на 7 и полученные результаты сложим.
(64 + 24) : 4 = 88 : 4 = 22
1) 64 + 24 = 88
2) 88 : 4 = 22
Сложим слагаемые и полученную сумму разделим на 4.
Оформляем задание в тетрадь.
1 2
28 · 3 − 57 = 84 − 57 = 27
2 1
34 + 13 · 5 = 15 + 65 = 99
2 1 3
98 – 23 ∙ 4 + 24 = 98 – 92 + 24 = 6 + 24 = 30
1 3 2
28 ∙ 2 – 13 ∙ 4 = 56 – 52 = 4
(49 + 28) : 7 = 49 : 7 + 28 : 7 = 7 + 4 = 11
(64 + 24) : 4 = 88 : 4 = 22
Номер 8.
Узнай площадь каждого квадрата и закрашенной его части.

Площадь квадратов 2 ∙ 2 = 4 см2.
Первый квадрат разбит на 4 равные части, значит, площадь одной – 1 см2.
Второй квадрат разбит на 4 равные части, значит, площадь закрашенной – 3 см2.
Третий квадрат разбит на 4 равные части, значит, площадь закрашенной – 2 см2.
1) Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Рассмотрим квадраты.
Все три квадрата равны.
Сторона каждого квадрата – 4 клетки = 2 см
2 см ∙ 2 см = 4 см2 – площадь каждого квадрата.
Продолжаем рассуждение.
Узнаем какая часть квадрата закрашена.
Квадрат 1. Фигура разделена на 4 равные части и закрашена одна из этих частей, значит закрашена одна четвертая часть.
Квадрат 2. Фигура разделена на 4 равные части и закрашено 3 из этих частей, значит закрашено три четвёртые части.
Квадрат 3. Фигура разделена на 4 равные части и закрашено 2 из этих частей, значит закрашено две четвёртые части.
Продолжаем рассуждение.
Узнаем площадь закрашенной части.
Первый квадрат. Чтобы найти площадь закрашенной части нужно площадь квадрата разделить на 4 одинаковые части и взять одну такую часть:
4 см2 : 4 = 1 см2 – площадь голубой части.
Второй квадрат. Чтобы найти площадь закрашенной части нужно площадь квадрата разделить на 4 одинаковые части и взять три такие части:
4 см2 : 4 ∙ 3 = 1 см2 ∙ 3 = 3 см2 – площадь розовой части.
Третий квадрат. Чтобы найти площадь закрашенной части нужно площадь квадрата разделить на 4 одинаковые части и взять две такие части:
4 см2 : 4 ∙ 2 = 1 см2 ∙ 2 = 2 см2 – площадь желтой части.
Оформляем задание в тетрадь.
2 см ∙ 2 см = 4 см2 – площадь каждого квадрата.
4 см2 : 4 = 1 см2 – площадь голубой части.
4 см2 : 4 ∙ 3 = 3 см2 – площадь розовой части.
4 см2 : 4 ∙ 2 = 2 см2 – площадь желтой части.
Задание внизу страницы
Вычисли.
Ответ:19 ∙ 4 − 38 = (10 + 9) · 4 - 38 = (40 + 36) − 38 = 76 − 38 = 38 43 − 27 + 32 : 4 = 43 − 27 + 8 = 16 + 8 = 24 (36 + 24) : 15 = 60 : 15 = 4 (подбором)
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
19 ∙ х = 38
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
32 : х = 2
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решаем уравнение.
19 ∙ х = 38
х = 38 : 19
х = 2
Ответ: 2.
32 : х = 2
х = 32 : 2
х = 16
Ответ: 16.
Делаем проверку.
19 ∙ х = 38
Проверка: вместо х подставим число 2.
1) 19 ∙ 2 = (10 + 9) ∙ 2 = 20 + 18 = 38
2) 38 = 38
Уравнение решено верно.
32 : х = 2
Проверка: вместо х подставим число 16.
1) 32 : 16 = 2
2) 2 = 2
Уравнение решено верно.
Объясни решение уравнений и проверку.
Ответ:
х – неизвестный делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестное делимое. Чтобы найти неизвестное делимое, нужно делитель умножить на частное. Чтобы это проверить, подставляем вместо х полученное значение.
Номер 1.
Реши уравнения с объяснением.
Ответ:
Номер 2.
Закончи выводы:
1) Чтобы найти неизвестный множитель, надо ... . 2) Чтобы найти неизвестное делимое, надо ... . 3) Чтобы найти неизвестный делитель, надо ... .
Ответ:1) ... произведение поделить на известный множитель. 2) ... частное умножить на делитель. 3) ... делимое поделить на частное.
Номер 3.
Ответ:

Номер 4.
В туристский поход пошли 19 человек. На каждого взяли по 2 банки мясных консервов и по 3 банки овощных. Сколько всего банок с консервами взяли?
Ответ:
Можно оформить с помощью таблицы:

1-й способ решения:
1) 2 + 3 = 5 (б.) – консервов взяли.
2) 5 ∙ 19 = 95 (б.)
Ответ: 95 банок взяли всего.
2-й способ решения:
1) 2 ∙ 19 = 38 (б.) – мясных консервов взяли.
2) 3 ∙ 19 = 57 (б.) – овощных консервов взяли.
3) 38 + 57 = 95 (б.)
Ответ: 95 банок взяли всего.
Номер 5.
Составь задачу по выражению (18 + 42) : 6.
Ответ:В ящики, каждый из которых вмещает по 6 кг разложили 18 кг мандарин и 42 кг апельсин. Сколько всего ящиков потребовалось?

(18 + 42) : 6 = 10 (ящ.)
Ответ: 10 ящиков потребовалось всего.
Номер 6.
(Устно.) Назови числа от 7 до 70, которые делятся на 7 без остатка.
Ответ:7, 14, 21, 28, 35, 42, 49, 56, 63, 70.
Номер 7.
Ответ:

Номер 8.
Узнай площадь каждого квадрата и закрашенной его части.

Площадь квадратов 2 ∙ 2 = 4 см2.
Первый квадрат разбит на 4 равные части, значит, площадь одной – 1 см2.
Второй квадрат разбит на 4 равные части, значит, площадь закрашенной – 3 см2.
Третий квадрат разбит на 4 равные части, значит, площадь закрашенной – 2 см2.
Задание внизу страницы
Реши уравнения.
19 · х = 38 32 : х = 2
Ответ:19 · х = 38
х = 38 : 19
х = 2
Проверка:
19 · 2 = 38
38 = 38
Ответ: х = 2
32 : х = 2
х = 32 : 2
х = 16
Проверка:
32 : 16 = 2
2=2
Ответ: х = 16
Номер 1.
Из данных уравнений выпиши и реши те, которые решаются делением.
Ответ:
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
х : 18 = 5
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Решается умножением.
х ∙ 11 = 55
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
96 : х = 16
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
52 : х = 13
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
х : 15 = 6
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Решается умножением.
15 ∙ х = 75
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
Решаем уравнение.
Решим уравнения, которые решаются делением.
х ∙ 11 = 55
х = 55 : 11
х = 5
96 : х = 16
х = 96 : 16
х = 6
52 : х = 13
х = 52 : 13
х = 4
15 ∙ х = 75
х = 75 : 15
х = 5
Делаем проверку.
х ∙ 11 = 55
Проверка: вместо х подставим число 5.
1) 11 ∙ 5 = (10 + 1) ∙ 5 = 50 + 5 = 55
2) 55 = 55
96 : х = 16
Проверка: вместо х подставим число 6.
1) 96 : 6 = (60 + 36) : 6 = 10 + 6 = 16
2) 16 = 16
52 : х = 13
Проверка: вместо х подставим число 4.
1) 52 : 4 = (40 + 12) : 4 = 10 = 3 = 13
2) 13 = 13
15 ∙ х = 75
Проверка: вместо х подставим число 5.
1) 15 ∙ 5 = (10 + 5) ∙ 5 = 50 + 25 = 75
2) 75 = 75
Оформляем задание в тетрадь.
х ∙ 11 = 55
х = 55 : 11
х = 5
5 ∙ 11 = 55
55 = 55
Ответ: х = 5.
96 : х = 16
х = 96 : 16
х = 6
96 : 6 = 16
16 = 16
Ответ: х = 6.
52 : х = 13
х = 52 : 13
х = 4
52 : 4 = 13
13 = 13
Ответ: х = 4.
15 ∙ х = 75
х = 75 : 15
х = 5
15 ∙ 5 = 75
75 = 75
Ответ: х = 5.
Номер 2.
Увеличь в 8 раз числа: 12, 9, 8, 11. Увеличь на 8 числа: 26, 37, 49, 58.
Ответ:12 ∙ 8 = 96
9 ∙ 8 = 72
8 ∙ 8 = 64
11 ∙ 8 = 88
26 + 8 = 34
37 + 8 = 45
49 + 8 = 57
58 + 8 = 66
1) Увеличь в 8 раз, значит, умножить на 8.
2) Увеличь на 8, значит, прибавить 8 единиц.
Увеличим числа в 8 раз.
12 ∙ 8 = (10 + 2) ∙ 8 = 10 ∙ 8 + 2 ∙ 8 = 80 + 16 = 96
9 ∙ 8 = 72
8 ∙ 8 = 64
11 ∙ 8 = (10 + 1) ∙ 8 = 10 ∙ 8 + 1 ∙ 8 = 80 + 8 = 88
Увеличим числа на 8.
26 + 8 = 20 + 6 + 8 = 20 + 14 = 34
37 + 8 = 30 + 7 + 8 = 30 + 15 = 45
49 + 8 = 40 + 9 + 8 = 40 + 17 = 57
58 + 8 = 50 + 8 + 8 = 50 + 16 = 66
Оформляем задание в тетрадь.
12 ∙ 8 = 96
9 ∙ 8 = 72
8 ∙ 8 = 64
11 ∙ 8 = 88
26 + 8 = 34
37 + 8 = 45
49 + 8 = 57
58 + 8 = 66
Номер 3.
Ответ:66 : 33 = 2 64 : 16 = 4 77 : 7 = 11
55 : 11 = 5 75 : 25 = 3 34 : 2 = 17
51 : 3 = 17 6 ∙ 12 = 72
84 : 7 = 12 98 : 2 = 49
1) Вспомни способ деления методом подбора.
2) Чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Вычислим деление методом подбора.
66 : 33 = ?
Пробуем в частном 2 и проверяем:
33 ∙ 2 = 66,
66 = 66, значит,
66 : 33 = 2.
55 : 11 = ?
Пробуем в частном 4 и проверяем:
11 ∙ 4 = 44,
44 < 55, число 4 не подходит.
Пробуем в частном 5 и проверяем:
11 ∙ 5 = 55,
55 = 55, значит,
55 : 11 = 5.
64 : 16 = ?
Пробуем в частном 3 и проверяем:
16 ∙ 3 = 48,
48 < 64, число 3 не подходит.
Пробуем в частном 4 и проверяем:
16 ∙ 4 = 64,
64 = 64, значит,
64 : 16 = 4.
75 : 25 = ?
Пробуем в частном 2 и проверяем:
25 ∙ 2 = 50,
50 < 75, число 2 не подходит.
Пробуем в частном 3 и проверяем:
25 ∙ 3 = 75,
75 = 75, значит,
75 : 25 = 3.
Применим метод деления числа на сумму.
77 : 7 = (70 + 7) : 7 = 70 : 7 + 7 : 7 = 10 + 1 = 11
Представим число 70 в виде суммы чисел 70 и 7, каждое слагаемое разделим на 7 и полученные результаты сложим.
34 : 2 = (20 + 14) : 2 = 20 : 2 + 14 : 2 = 10 + 7 = 17
Представим число 34 в виде суммы чисел 20 и 14, каждое слагаемое разделим на 2 и полученные результаты сложим.
51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
Представим число 51 в виде суммы чисел 30 и 21, каждое слагаемое разделим на 3 и полученные результаты сложим.
84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12
Представим число 84 в виде суммы чисел 70 и 14, каждое слагаемое разделим на 7 и полученные результаты сложим.
6 ∙ 12 = 6 ∙ (10 + 2) = 6 ∙ 10 + 6 ∙ 2 = 60 + 12 = 72
Представим число 12 в виде суммы чисел 10 и 2, каждое слагаемое умножим на 6 и полученные результаты сложим.
98 : 2 = (80 + 18) : 2 = 80 : 2 + 18 : 2 = 40 + 9 = 49
Представим число 98 в виде суммы чисел 80 и 18, каждое слагаемое разделим на 2 и полученные результаты сложим.
Оформляем задание в тетрадь.
66 : 33 = 2
55 : 11 = 5
64 : 16 = 4
75 : 25 = 3
77 : 7 = (70 + 7) : 7 = 10 + 1 = 11
34 : 2 = (20 + 14) : 2 =10 + 7 = 17
51 : 3 = (30 + 21) : 3 = 10 + 7 = 17
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
6 ∙ 12 = 6 ∙ (10 + 2) = 60 + 12 = 72
98 : 2 = (80 + 18) : 2 = 40 + 9 = 49
Номер 4.
Выполни действия и сделай проверку.
Ответ:27 ∙ 3 = 81 99 : 11 = 9
Проверка: Проверка
81 : 3 = 27 9 ∙ 11 = 99
27 = 27 99 = 99
4 ∙ 18 = 72 91 : 7 = 13
Проверка: Проверка:
72 : 18 = 4 13 ∙ 7 = 91
4 = 4 91 = 91
1) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81
Представим число 27 в виде суммы чисел 20 и 7, каждое слагаемое умножим на 3 и полученные результаты сложим.
99 : 11 = ?
Пробуем в частном 8 и проверяем:
11 ∙ 8 = 88,
88 < 99, число 8 не подходит.
Пробуем в частном 9 и проверяем:
11 ∙ 9 = 99,
99 = 99, значит,
99 : 11 = 9.
4 ∙ 18 = 4 ∙ (10 + 8) = 4 ∙ 10 + 4 ∙ 8 = 40 + 32 = 72
Представим число 18 в виде суммы чисел 10 и 8, каждое слагаемое умножим на 4 и полученные результаты сложим.
91 : 7 = (70 + 21) : 7 = 70 : 7 + 21 : 7 = 10 + 3 = 13
Представим число 91 в виде суммы чисел 70 и 21, каждое слагаемое разделим на 7 и полученные результаты сложим.
Делаем проверку.
27 ∙ 3 = 81
Проверка:
81 : 3 = (60 + 21) : 3 = 60 : 3 + 21 : 3 = 20 + 7 = 27
27 = 27
Решение выполнено верно.
99 : 11 = 9
Проверка:
11 ∙ 9 = (10 + 1) ∙ 9 = 10 ∙ 9 + 1 ∙ 9 = 90 + 9 = 99
99 = 99
Решение выполнено верно.
4 ∙ 18 = 72
Проверка:
72 : 4 = (40 + 32) : 4 = 40 : 4 + 32 : 4 = 10 + 8 = 18
18 = 18
Решение выполнено верно.
91 : 7 = 13
Проверка:
13 ∙ 7 = (10 + 3) ∙ 7 = 10 ∙ 7 + 3 ∙ 7 = 70 + 21 = 91
91 = 91
Решение выполнено верно.
Оформляем задание в тетрадь.
27 ∙ 3 = 81
Проверка:
81 : 3 = 27
27 = 27
99 : 11 = 9
Проверка:
11 ∙ 9 = 99
99 = 99
4 ∙ 18 = 72
Проверка:
72 : 4 = 18
18 = 18
91 : 7 = 13
Проверка:
13 ∙ 7 = 91
91 = 91
Номер 5.
Ответ:90 : 5 > 90 : 10, потому что при одинаковых делимых частное будет больше, когда делитель меньше.
35 ∙ 1 = 35 ∙ 0 + 35
48 : 4 < 52 : 4, потому что при одинаковых делителях частное будет больше, когда делимое больше.
35 + 1 > (35 + 0) ∙ 1
Можно такое оформление выбрать:

1) Равенство – это запись, в которой есть знак равно.
2) Неравенство – это запись, в которой есть знак больше или меньше.
Рассуждаем.
90 : 5 > 90 : 10
Так как при одинаковых делимых частное будет больше, когда делитель меньше.
48 : 4 < 52 : 4
Так как при одинаковых делителях частное будет больше, когда делимое больше.
35 ∙ 1 = 35 ∙ 0 + 35
35 = 35
Если число умножить на 1, то число не изменится.
Если число умножить на 0, то произведение равно 0.
35 + 1 > (35 + 0) ∙ 1
Если к числу прибавить 1, то число увеличится на 1.
Если к числу прибавить 0, то число не изменится.
Если число умножить на 1, то получится тоже число.
Выполним проверку.
90 : 5 > 90 : 10
90 : 5 = 18
90 : 10 = 9
18 > 9
48 : 4 < 52 : 4
48 : 4 = 12
52 : 4 = 13
12 < 13
35 ∙ 1 = 35 ∙ 0 + 35
35 ∙ 1 = 35
35 ∙ 0 + 35 = 0 ∙ 35 = 35
35 = 35
35 + 1 > (35 + 0) ∙ 1
35 + 1 = 36
(35 + 0) ∙ 1 = 35
36 > 35
Оформляем задание в тетрадь.
90 : 5 > 90 : 10
48 : 4 < 52 : 4
35 ∙ 1 = 35 ∙ 0 + 35
35 + 1 > (35 + 0) ∙ 1
Номер 6.
На полную зарядку первых дронов уходило 36 мин, а после доработки системы зарядки – 12 мин. Во сколько раз ускорилась зарядка дронов? На сколько минут ускорилась зарядка дронов?

1) 36 : 12 = 3 (р.) – во сколько раз ускорилась зарядка; 2) 36 – 12 = 24 (мин) – на сколько ускорилась зарядка. Ответ: в 3 раза ускорилась зарядка; на 24 минуты ускорилась зарядка дронов.
1) Если уменьшилась во сколько – то раз, значит, нужно большее разделить на меньшее.
2) Если уменьшилась на сколько – то, значит, нужно из большего вычесть меньшее.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Известно, что на полную зарядку дронов уходило 36 мин, а после доработки системы – 12 мин. Нам нужно узнать, во сколько раз ускорилась зарядка. Ускорилась, значит, продолжительность стала меньше. Чтобы узнать, во сколько раз меньше времени стало уходить на зарядку, нужно время «до» разделить на время «после».
36 : 12 = 3 (раза) – во столько раз ускорилась зарядка.
Продолжаем рассуждения.
Теперь нам нужно узнать, на сколько минут ускорилась зарядка. Для этого нужно из времени «до» вычесть время «после».
36 – 12 = 24 (мин) – на столько ускорилась зарядка.
Записываем ответ.
Ответ: в 3 раза ускорилась зарядка, на 24 минуты ускорилась зарядка.
Номер 7.
Какое самое большое число до 26 делится без остатка на 3? на 4? на 5? на 6? на 9? на 10?
Ответ:24 : 3 = 8 24 : 4 = 6 25 : 5 = 5 24 : 6 = 4 18 : 9 = 2 20 : 10 = 2
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Выпишем все числа до 26.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26.
Вспомним таблицу умножения на 3, на 4, на 5, на 6, на 9, на 10.
Выпишем нужные числа и проверим.
Самое большое число до 26, которое делится без остатка на 3 – это число 24
24 : 3 = 8,
так как следующее число, которое делится на 3 – это 27.
Самое большое число до 26, которое делится без остатка на 4 – это число 24
24 : 4 = 6,
так как следующее число, которое делится на 4 – это 28.
Самое большое число до 26, которое делится без остатка на 5 – это число 25
25 : 5 = 5,
так как следующее число, которое делится на 5 – это 30.
Самое большое число до 26, которое делится без остатка на 6 – это число 24
24 : 6 = 4,
так как следующее число, которое делится на 6 – это 30.
Самое большое число до 26, которое делится без остатка на 9 – это число 18
18 : 9 = 2,
так как следующее число, которое делится на 9 – это 27.
Самое большое число до 26, которое делится без остатка на 10 – это число 20
20 : 10 = 2,
так как следующее число, которое делится на 10 – это 30.
Оформляем задание в тетрадь.
24 : 3 = 8
24 : 4 = 6
25 : 5 = 5
24 : 6 = 4
18 : 9 = 2
20 : 10 = 2
Номер 8.
Ответ:45 : 15 = 3 99 : 33 = 3 80 : 16 = 5

При необходимости 2 и 3 столбики можно расписать подробнее:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Вычисляем методом подбора.
45 : 15 = ?
Пробуем в частном 2 и проверяем:
15 ∙ 2 = 30,
30 < 45, число 3 не подходит.
Пробуем в частном 3 и проверяем:
15 ∙ 3 = (10 + 5) ∙ 3 = 30 + 15 = 45,
45 = 45, значит,
45 : 15 = 3.
99 : 33 = ?
Пробуем в частном 2 и проверяем:
33 ∙ 2 = 66,
66 < 99, число 2 не подходит.
Пробуем в частном 3 и проверяем:
33 ∙ 3 = (30 + 3) ∙ 3 = 90 + 9 = 99,
99 = 99, значит,
99 : 33 = 3.
80 : 16 = ?
Пробуем в частном 4 и проверяем:
16 ∙ 4 = 54,
54 < 80, число 4 не подходит.
Пробуем в частном 5 и проверяем:
16 ∙ 5 = (10 + 6) ∙ 5 = 50 + 30 = 80,
80 = 80, значит,
80 : 16 = 5.
Вычисляем по действиям.
78 : 6 ∙ 3 = 39
1) 78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
2) 13 ∙ 3 = (10 + 3) ∙ 3 = 30 + 9 = 39
51 : 3 ∙ 4 = 68
1) 51 : 3 = (30 + 21) : 3 = 10 + 7 = 17
2) 17 ∙ 4 = (10 + 7) ∙ 4 = 40 + 28 = 68
84 : 4 ∙ 3 = 63
1) 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21
2) 21 ∙ 3 = (20 + 1) ∙ 3 = 60 + 3 = 63
100 – 4 ∙ 18 = 28
1) 4 ∙ 18 = 4 ∙ (10 + 8) = 40 + 32 = 72
2) 100 – 72 = 28
100 – 6 ∙ 13 = 22
1) 6 ∙ 13 = 6 ∙ (10 + 3) = 60 + 18 = 78
2) 100 – 78 = 22
100 – 4 ∙ 25 = 0
1) 4 ∙ 25 = 4 ∙ (20 + 5) = 80 + 20 = 100
2) 100 – 100 = 0
(34 + 36) : 10 = 7
1) 34 + 36 = 70
2) 70 : 10 = 7 дес. : 1 дес. = 7 : 1 = 7
(75 – 33) : 3 = 14
1) 75 – 33 = 42
2) 42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
(82 – 16) : 33 = 2
1) 82 – 16 = 66
2) 66 : 33 = 2
Оформляем задание в тетрадь.
45 : 15 = 3
99 : 33 = 3
80 : 16 = 5
78 : 6 ∙ 3 = 13 ∙ 3 = 39
51 : 3 ∙ 4 = 17 ∙ 4 = 68
84 : 4 ∙ 3 = 21 ∙ 3 = 63
100 – 4 ∙ 18 = 100 – 72 = 28
100 – 6 ∙ 13 = 100 – 78 = 22
100 – 4 ∙ 25 = 100 – 100 = 0
(34 + 36) : 10 = 70 : 10 = 7
(75 – 33) : 3 = 42 : 3 = 14
(82 – 16) : 33 = 66 : 33 = 2
Номер 9.
От Москвы до Ставрополя поезд идет 28 ч, а самолёт тратит в 14 раз меньше времени, чем поезд. Сколько часов экономит самолёт для пассажира?
Ответ:
1) 28 : 14 = 2 (ч) – летит самолёт. 2) 28 – 2 = 26 (ч) Ответ: 26 часов экономит самолёт для пассажиров.
«В 14 раз меньше» – решается делением.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Самолет тратит времени в 14 раз меньше, чем поезд. Значит, чтобы найти сколько времени потратит самолет от Москвы до Ставрополя, нужно время пути поезда уменьшить в 14 раз, то есть разделить на 14.
28 : 14 = 2 (ч.) – летит самолет.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Значит, чтобы узнать, сколько часов экономит самолет, нужно из времени, которое идёт поезд, вычесть время, которое летит самолет.
28 – 2 = 26 (ч.) – столько экономит самолет для пассажира.
Записываем ответ.
Ответ: 26 часов экономит самолет для пассажира.
Решение выражением: 28 – 28 : 14 = 26 (ч), где 28 : 14 – время самолета в пути.
Номер 10.
Определи, не вычисляя, меньшую из данных сумм. Проверь вычислением.
1) 27 + 48 + 16 + 9 2) 47 + 25 + 8 + 13 3) 18 + 10 + 50 + 28
Ответ:47 + 25 + 8 + 13 – наименьшая сумма.
1) 27 + 48 + 16 + 9 = 75 + 25 = 100
2) 47 + 25 + 8 + 13 = (47 + 13) + 25 + 8 = 60 + 25 + 8 = 85 + 8 = 93
3) 18 + 10 + 50 + 28 = (10 + 50) + (18 + 28) = 60 + 46 = 106
Внимательно рассмотри выражения и сравни каждое слагаемое.
Рассуждаем.
В примере, в котором наименьшие слагаемые, то и будет наименьшим.
Сравним каждое слагаемое из 2 примера с другими слагаемыми из 1 и 3 примера.
1) 27 + 48 + 16 + 9
2) 47 + 25 + 8 + 13
3) 18 + 10 + 50 + 28
48 > 47, 47 < 50
1) 27 + 48 + 16 + 9
2) 47 + 25 + 8 + 13
3) 18 + 10 + 50 + 28
27 > 25, 25 < 28
1) 27 + 48 + 16 + 9
2) 47 + 25 + 8 + 13
3) 18 + 10 + 50 + 28
9 > 8, 8 < 10
1) 27 + 48 + 16 + 9
2) 47 + 25 + 8 + 13
3) 18 + 10 + 50 + 28
16 > 13, 13 < 18
Делаем вывод.
47 + 25 + 8 + 13 – наименьшая сумма.
Проверяем вычислением.
1) 27 + 48 + 16 + 9 = 75 + 25 = 100
2) 47 + 25 + 8 + 13 = 72 + 21 = 93
3) 18 + 10 + 50 + 28 = 28 + 78 = 106
Задание на полях страницы
Начерти и продолжи:


1) Диаметр – отрезок, который проходит через центр и соединяет две любые точки на окружности.
2) Используй специальные приборы: циркуль и линейку.
Рассуждаем.
Рассмотрим рисунок.
Радиус каждой окружности равен 15 мм = 1 см 5 мм. Каждая следующая окружность начинается с центра предыдущей окружности.
Начертим.
.jpg)
Задание внизу страницы
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.