Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 110

Учебник 2 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 2.
Год: 2021-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличается задание? Переключите год учебника.

2021 2024

Ответ к учебнику по математике 3 класс 2 часть Моро, Бантова, Бельтюкова страница 110

Проверим себя и оценим свои достижения

Тексты для итоговой контрольной работы

Задания базового уровня

Номер 1.

Восстанови пропущенные числа. 786, 787, 788, ..., ..., ..., 792.

Ответ:

789, 790, 791

Подсказка:

Прежде, чем дополнить ряд чисел, необходимо выявить закономерность, т.е. правило, как он составлен.

Шаг 1.
Рассуждаем и выполняем вычисления.

Если рассмотреть ряд чисел, то видно, что каждое следующее число на 1 единицу больше предыдущего числа.

Найдём эти числа:
786 + 1 = 787
787 + 1 = 788
788 + 1 = 789
789 + 1 = 790
790 + 1 = 791
791 + 1 = 792

Шаг 2.
Оформляем задание в тетрадь.

786, 787, 788, 789, 790, 791, 792.

Номер 2.

Ответ:

460 + 320 = (400 + 300) + (60 + 20) = 780 780 − 650 = (700 - 600) + (80 - 50) = 100 + 30 = 130
84 : 7 = 12 3 ∙ 19 = 57
100 − 56 : (38 − 30) = 100 - 56 : 8 = 100 - 7 = 93 96 − 48 : 8 ∙ 6 = 96 - 6 * 6 = 96 - 36 = 60

Подсказка:

1) Вспомни алгоритм вычисления по разрядам.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

Шаг 1.
Рассуждаем и вычисляем.

Выполним сложение и вычитание по разрядам.

460 + 320 = (400 + 300) + (60 + 20) = 700 + 80 = 780

Сотни складываем с сотнями, десятки с десятками и единицы с единицами.

780 − 650 = (700 – 600) + (80 + 50) = 100 + 30 = 130

Из сотен вычитаем сотни, из десяток десятки и из единиц единицы.

Выполним деление и умножение с помощью правила деления и умножения суммы на число.

84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12

Представим число 84 в виде суммы чисел 70 и 14. Каждое слагаемое разделим на 7 и полученные результаты сложим.

3 ∙ 19 = 3 ∙ (10 + 9) = 3 ∙ 10 + 3 ∙ 9 = 30 + 27 = 57

Представим число 19 виде суммы чисел 10 и 9. Каждое слагаемое умножим на 3 и полученные результаты сложим.

Выполним вычисления по действиям.

100 − 56 : (38 − 30) = 93
Первым действием выполним в скобках – вычитание, потом – деление и последним действие вне скобок – вычитание. 1) 38 – 30 = 8
2) 56 : 8 = 7
3) 100 – 7 = 93

96 − 48 : 8 ∙ 6 = 60
Первым действием выполним деление, потом – умножение и последним – вычитание.
1) 48 : 8 = 6
2) 6 ∙ 6 = 36
3) 96 – 36 = 60

Шаг 2.
Оформляем задание в тетрадь.

460 + 320 = 780
780 − 650 = 130

84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
3 ∙ 19 = 3 ∙ (10 + 9) = 30 + 27 = 57

100 − 56 : (38 − 30) = 100 – 56 : 8 = 100 – 7 = 93

96 − 48 : 8 ∙ 6 = 96 – 6 ∙ 6 = 96 – 36 = 60

Номер 3.

Вычисли и проверь.

Ответ:

Подсказка:

Вспомни алгоритм сложения и вычитания в столбик.

Шаг 1.
Выполним вычисления с пояснениями.

Выполним сложение.

Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц: 5 + 5 = 10
10 ед. – это 1 дес. и 0 ед.
Пишем 0 ед. в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки: 9 + 4 + 1 = 14
14 дес. – это 1 сот. и 4 дес.
Пишем 4 дес. в ответе под десятками, а 1 сот. пойдет в разряд сотен.
Складываем сотни: 4 + 2 + 1 = 7.
7 пишем в ответе в разряде сотен.
Ответ: 740.

Выполним вычитание.

Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц: 9 – 6 = 3
Пишем 3 в ответе в разряде единиц.
Вычитаем десятки: Из 5 дес. нельзя отнять 7 дес., поэтому занимаем 1 единицу у сотен.
1 сот. и 5 дес. – это 15 дес.
15 – 7 = 8
8 пишем в ответе под десятками.
Вычитаем сотни: Было 6 сот., но 1 сот. взяли при вычитании десяток, поэтому осталось 5 сот.
5 – 3 = 2
2 пишем в ответ в разделе сотни.
Ответ: 283.

Шаг 2.
Сделаем проверку.

495 + 245 = 740
Проверка: чтобы выполнить проверку нужно из суммы вычесть один из множителей.

Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 0 отнять 5 нельзя, поэтому занимает 1 единицу у десяток
1 дес. и 0 ед. – это 10 ед.
10 – 5 = 5.
Пишем 5 в ответ в разряде единиц.
Вычитаем десятки: было 4 дес. заняли 1 дес. и осталось 3 дес.
Из 3 дес. нельзя отнять 4 дес., поэтому занимаем 1 единицу у сотен.
1 сот. и 3 дес. – это 13 дес.
13 – 4 = 9
9 пишем в ответе под десятками.
Вычитаем сотни: Было 7 сот., но 1 сот. взяли при вычитании десяток, поэтому осталось 6 сот.
6 – 2 = 4
4 пишем в ответ в разделе сотни.
Ответ: 495.

659 – 376 = 283
Проверка: чтобы выполнить проверку нужно к разности прибавить вычитаемое.

Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц: 3 + 6 = 9
Пишем 9 в ответе в разряде единиц.
Складываем десятки: 8 + 7 = 15
15 дес. – это 1 сот. и 5 дес.
Пишем 5 дес. в ответе под десятками, а 1 сот. пойдет в разряд сотен.
Складываем сотни: 2 + 3 + 1 = 6.
6 пишем в ответе в разряде сотен.
Ответ: 659.

Шаг 3.
Оформим задание в тетрадь.

Номер 4.

В 8 одинаковых бочонках 72 кг меда. Сколько меда в 10 таких бочонках?

Ответ:

1) 72 : 8 = 9 (кг) – в 1 бочонке. 2) 9 ∙ 10 = 90 (кг) Ответ: 90 кг мёда всего в 10 бочонках.

Подсказка:

Данная задача вида: «Масса 1 бочонка, количество бочонков, общая масса» характеризуется зависимостями между элементами:
Масса 1 бочонка · количество бочонков = общая масса.
Общая масса : масса 1 бочонка = количество бочонков.
Общая масса : количество бочонков = масса 1 бочонка.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Масса каждого бочонка одинакова.
Чтобы узнать массу одного бочонка нужно общую массу разделить на количество бочонков.

72 : 8 = 9 (кг) – масса 1 бочонка.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать массу 10 таких же бочонков нужно массу 1 бочонка умножить на количество бочонков, то есть на 10.

9 ∙ 10 = 90 (кг) – масса 10 бочонков.

Шаг 4.
Записываем ответ.

Ответ: 90 кг.

Решение выражением:
72 : 8 ∙ 10 = 90 (кг) – масса 10 бочонков,
где 72 : 8 – масса 1 бочонка.

Номер 5.

Папе 30 лет, а сыну 6 лет. Во сколько раз папа старше сына?

Ответ:

30 : 6 = 5 (р.) Ответ: в 5 раз папа старше сына.

Подсказка:

«Во сколько раз больше» – вычисляется делением.

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
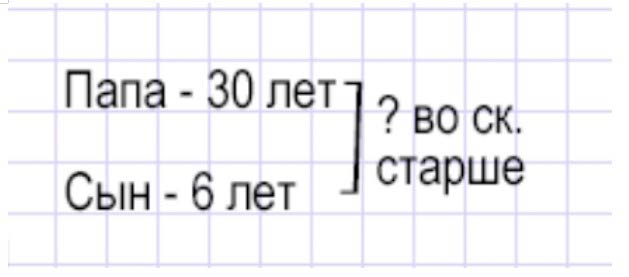
Рассуждаем.

Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.

30 : 6 = 5 (раз) – во сколько раз папа старше сына.

Шаг 3.
Записываем ответ.

Ответ: в 5 раз.

Номер 6.

Найди периметр прямоугольника со сторонами 7 см и 3 см.

Ответ:

(7 + 3) ∙ 2 = 20 (см) Ответ: периметр прямоугольника – 20 см.

Подсказка:

Периметр – это сумма длин всех сторон.

Шаг 1.
Рассуждаем.

У прямоугольника стороны попарно равны, то есть противоположные стороны равны.
Периметр прямоугольника можно вычислить по формуле – сумма длины и ширины умножить на 2.

Шаг 2.
Вычисляем.

(7 + 3) ∙ 2 = 10 ∙ 2 = 20 (см) – периметр прямоугольника.

Шаг 3.
Записываем ответ.

Ответ: 20 см.

Номер 7.

Найди площадь квадрата со стороной 5 дм.

Ответ:

5 ∙ 5 = 25 (дм²) Ответ: площадь квадрата – 25 дм²

Подсказка:

1) Площадь – часть плоскости, которую занимает фигура.

2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Шаг 1.
Вычисляем.

Чтобы вычислить площадь квадрата нужно длину умножить на ширину, но у квадрата все стороны равны, значит нужно сторону квадрата умножить два раза.

5 дм ∙ 5 дм = 25 дм² – площадь квадрата.

Шаг 2.
Записываем ответ.

Ответ: 25 дм².

Математика 2 часть. 3 класс - Учебник. Моро. Страница 110. Год 2024

Задания повышенного уровня

Номер 1.

Определи, по какому правилу составлен числовой ряд, и восстанови пропущенные числа. 638, 648, 658, ..., ..., ..., 698

Ответ:

668, 678, 688

Подсказка:

Прежде, чем дополнить ряд чисел, необходимо выявить закономерность, т.е. правило, как он составлен.

Шаг 1.
Рассуждаем и выполняем вычисления.

Если посмотреть на ряд чисел, то видно, что каждое последующее число на 10 больше предыдущего.

Найдём числа:
638 + 10 = 648
648 + 10 = 658
658 + 10 = 668
668 + 10 = 678
678 + 10 = 688
688 + 10 = 698

Шаг 2.
Оформляем задание в тетрадь.

638, 648, 658, 668, 678, 688, 698.

Номер 2.

2) Поставь скобки так, чтобы стало верным равенство 300 − 4 ∙ 90 − 40 = 100.

Ответ:

1) 430 + 70 = 570 − 70 96 : 16 = 6 240 + 130 = 390 − 20 5 ∙ 15 = 75
2) 300 − 4 ∙ (90 − 40) = 100

Подсказка:

1) Вспомни, как найти неизвестное слагаемое, уменьшаемое, делитель и множитель.

2) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.

Задание 1.

Шаг 1.
Рассуждаем и выполняем вычисления.

Рассмотрим 1 выражение.
430 + = 570 – 70
Упростим выражение вычислив значение в правой части.
570 – 70 = 500
Получим новое выражение:
430 + = 500
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
500 – 430 = 70
Получится равенство: 430 + 70 = 570 – 70

Рассмотрим 2 выражение.
240 + 130 = – 20
Упростим выражение вычислив значение в левой части.
240 + 130 = 370
Получим новое выражение:
370 = – 20
Чтобы найти уменьшаемое, нужно у разности прибавить вычитаемое.
370 + 20 = 390
Получится равенство: 240 + 130 = 390 – 20

Рассмотрим 3 выражение.
96 : = 6
Чтобы найти делитель, нужно делимое разделить на частное.
96 : 6 = (60 + 36) : 6 = 10 + 6 = 16
Получится равенство: 96 : 16 = 6

Рассмотрим 4 выражение.
∙ 15 = 75
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
75 : 15 = 5
Получится равенство: 5 ∙ 15 = 75

Задание 2.

Шаг 2.
Расставим скобки.

300 − 4 ∙ (90 − 40) = 100
Первым действием выполним вычитание в скобках, потом – умножение и потом – вычитание без скобок.

1) 90 – 40 = 50
2) 4 ∙ 50 = 4 ∙ 5 дес. = 20 дес. = 200
3) 300 – 200 = 100

Шаг 3.
Оформляем задание в тетрадь.

1)
430 +     = 570 – 70
430 +     = 500
500 – 430 = 70

240 + 130 =     – 20
370 =     – 20
370 + 20 = 390

96 :     = 6
96 : 6 = (60 + 36) : 6 = 10 + 6 = 16

    ∙ 15 = 75
75 : 15 = 5

2)
300 − 4 ∙ (90 − 40) = 300 – 4 ∙ 50 = 300 – 200 = 100

Номер 3.

Ответ:

Подсказка:

Вспомни алгоритм сложение и вычитание в столбик.

Рассмотрим первый ребус.

Шаг 1.
Рассуждаем и выполняем вычисления.

Рассмотрим разряд единиц.
Неизвестно количество единиц в сумме.
Чтобы найти это число, нужно сложить количество единиц первого и второго слагаемого.
8 + 5 = 13 – это 1 дес. и 3 ед.
Значит, в сумме 3 единицы, а 1 дес. запоминаем и прибавим при сложении десятков.

Шаг 2.
Продолжаем рассуждение.

Рассмотрим разряд десятков.
Неизвестно количество десятков второго слагаемого.
Чтобы найти десятки второго слагаемого, нужно из количества десятков суммы вычесть количество десятков первого слагаемого.
9 дес. – 7 дес. = 2 дес.
Вспомним, что 1 ед. десятков ушла в единицы при сложении единиц, поэтому 2 дес – 1 дес. = 1 дес.
Значит, во втором слагаемом 1 десяток.

Шаг 3.
Продолжаем рассуждение.

Рассмотрим разряд сотен.
Неизвестно количество сотен первого слагаемого.
Чтобы найти сотни первого слагаемого, нужно из количества сотен суммы вычесть количество сотен второго слагаемого.
6 сот. – 4 сот. = 2 сот.
Значит, в первом слагаемом 2 сотни.

Получим:

Рассмотрим второй ребус.

Шаг 4.
Рассуждаем и выполняем вычисления.

Рассмотрим разряд единиц.
Неизвестно количество единиц в уменьшаемом.
Чтобы найти это число, нужно сложить количество единиц вычитаемого и разности.
8 + 8 = 16 – это 1 дес. и 6 ед.
Значит, в уменьшаемом 6 единиц, а 1 дес. занимали у десятков.

Шаг 5.
Продолжаем рассуждение.

Рассмотрим разряд десятков.
Неизвестно количество десятков в вычитаемом.
Чтобы найти десятки вычитаемого, нужно из количества десятков уменьшаемого вычесть количество десятков разности.
4 – 2 – 1 (занимали) = 1
Значит, в вычитаемом 1 десяток.

Шаг 6.
Продолжаем рассуждение.

Рассмотрим разряд сотен.
Неизвестно количество сотен в разности.
Чтобы найти сотни в разности, нужно из количества сотен уменьшаемого вычесть количество сотен вычитаемого.
5 – 1 = 4
Значит, в разности 4 сотни.

Получим:

Шаг 7.
Оформляем задание в тетрадь.

Номер 4.

За 5 одинаковых по цене открыток заплатили 70 р. Сколько таких открыток можно купить на 98 р.?

Ответ:

1) 70 : 5 = 14 (р.) – за 1 открытку. 2) 98 : 14 = 7 (откр.) Ответ: 7 открыток можно купить на 98 рублей.

Подсказка:

Данная задача вида: «Количество открыток, цена 1 открытки, общая стоимость» характеризуется зависимостями между элементами:
Цена 1 открытки · количество открыток = общая стоимость.
Общая стоимость : цена 1 открытки = количество открыток.
Общая стоимость : количество открыток = масса 1 открытки.

Шаг 1.
Оформляем краткую запись.

5 открыток – 70 рублей
? открыток – 98 рублей

Шаг 2.
Рассуждаем.

Цена каждой открытки одинакова. Чтобы узнать цену одной открытки, нужно общую стоимость разделить на количество открыток.

70 : 5 = (50 + 20) : 5 = 10 + 4 = 14 (р.) – стоимость 1 открытки.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько можно купить открыток на 98 рублей, нужно общую стоимость разделить на стоимость одной открытки.

98 : 14 = 7 (отк.) – можно купить на 98 рублей.

Шаг 4.
Записываем ответ.

Ответ: 7 открыток можно купить на 98 рублей.

Номер 5.

В двух одинаковых по массе корзинах 28 кг яблок, а в одном пакете – 2 кг. Во сколько раз корзина с яблоками тяжелее, чем пакет с яблоками?

Ответ:

1) 28 : 2 = 14 (кг) – в 1 корзине. 2) 14 : 2 = 7 (р.) Ответ: корзина с яблоками в 7 раз тяжелее, чем пакет с яблоками.

Подсказка:

«Во сколько раз» – вычисляется делением.

Шаг 1.
Оформляем краткую запись.

2 корзины – 28 кг яблок
1 пакет – 2 кг яблок
Во сколько раз корзина с яблоками тяжелее, чем пакет с яблоками?

Шаг 2.
Рассуждаем.

В каждой корзине одинаковое количество яблок.
Значит, чтобы узнать, сколько яблок в каждой корзине, нужно общую массу яблок разделить на количество корзин.

28 : 2 = 14 (кг) – в одной корзине.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.

14 : 2 = 7 (раз) – во столько раз тяжелее.

Шаг 4.
Записываем ответ.

Ответ: в 7 раз корзина с яблоками тяжелее, чем пакет с яблоками.

Номер 6.

Периметр прямоугольника равен 18 см, а длина одной его стороны равна 4 см. Найди длину другой стороны этого прямоугольника.

Ответ:

Р = 18 см
а = 4 см
b = ? см
Р = (а + b) * 2, значит, b = P : 2 - а
18 : 2 − 4 = 5 (см)
Ответ: длина другой стороны равна 5 см.

Подсказка:

Периметр – это сумма длин всех сторон.

Шаг 1.
Рассуждаем.

У прямоугольника противоположные стороны равны.
Мы знаем, что периметр прямоугольника можно вычислить – сумму длины и ширины умножив на 2.
Значит, если периметр прямоугольника разделить на 2, то узнаем сумму длины и ширины или полупериметр прямоугольника.

18 : 2 = 9 (см) — сумма длины и ширины прямоугольника.

Шаг 2.
Продолжаем рассуждение.

Чтобы вычислить сторону прямоугольника, нужно из суммы сторон вычесть известную сторону.

9 – 4 = 5 (см) – длина второй стороны.

Шаг 3.
Записываем ответ.

Ответ: длина другой стороны равна 5 см.

Номер 7.

Площадь квадрата 36 дм². Найди длину его стороны и вырази ее в сантиметрах.

Ответ:

Площадь квадрата = a ∙ a 36 = 6 ∙ 6 Длина стороны квадрата – 6 дм = 60 см. Ответ: Ответ: длина стороны квадрата 60 см.

Подсказка:

1) Площадь – часть плоскости, которую занимает фигура.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
3) Помни, что 1 дм = 10 см.

Шаг 1.
Рассуждаем.

Чтобы вычислить площадь квадрата, нужно длину умножить на ширину, но у квадрата все стороны равны, значит нужно сторону квадрата умножить два раза. По условию задачи площадь квадрата равна 36 дм².
Поберём такое число, которое при умножении само на себя равно 36.
Это число 6, так как 6 ∙ 6 = 36.
Значит, сторона квадрата равна 6 дм.

Шаг 2.
Продолжаем рассуждение.

Переведем сторону квадрата в сантиметры.

6 дм = 6 ∙ 10 см = 60 см – длина квадрата.

Шаг 3.
Записываем ответ.

Ответ: длина стороны квадрата равна 60 см.

Конец страницы