Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 65

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 65

Номер 1.

Ответ:

64 : 8 = 8 7 ∙ 7 = 49 72 : 9 = 8 8 ∙ 8 = 64 81 : 9 = 9 9 ∙ 9 = 81 56 : 8 = 7 6 ∙ 6 = 36

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 65, номер 1

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо. 40 Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.

Шаг 1.
Выполним деление.

64 : 8 = 8, так как 8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

72 : 9 = 8, так как 9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

81 : 9 = 9, так как 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

56 : 8 = 7, так как 8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

Шаг 2.
Выполним умножение.

7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

Шаг 3.
Выполним вычисления по действиям.

1 2
(36 – 28) · 5 = 40

В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом вне скобок – умножение.

1) 36 – 28 = 36 – (26 + 2) = (36 – 26) – 2 = 10 – 2 = 8

Представим число 28 в виде суммы чисел 26 и 2. Вначале из числа 36 вычтем число 26, а потом вычтем число 2.

2) 8 ∙ 5 = 40

2 1
4 ∙ (23 – 16) = 28

1) 23 – 16 = 23 – (13 + 3) = (23 – 13) – 3 = 10 – 3 = 7

Представим число 16 в виде суммы чисел 13 и 3. Вначале из числа 23 вычтем число 13, а потом вычтем число 3.

2) 4 ∙ 7 = 28

1 2
(32 – 27) ∙ 6 = 30

1) 32 – 27 = 32 – (22 + 5) = (32 – 22) – 5 = 10 – 5 = 5

Представим число 27 в виде суммы чисел 22 и 5. Вначале из числа 32 вычтем число 22, а потом вычтем число 5.

2) 5 ∙ 6 = 30

2 1
5 ∙ (64 – 60) = 20

1) 64 – 60 = (60 – 60) + (4 – 0) = 4

Из десяток вычитаем десятки, а из единиц вычитаем единицы.

2) 5 ∙ 4 = 20

2 1
36 + 24 : 6 = 40

В данном выражении присутствуют действия сложение и деление. Вначале выполним деление, а потом выполним сложение.

1) 24 : 6 = 4, так как 6 · 4 = 24

2) 36 + 4 = 30 + (6 + 4) = 30 + 10 = 40

К десяткам прибавляем десятки, а к единицам прибавляем единицы.

1 2
45 : 5 · 9 = 81

В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1) 45 : 5 = 9, так как 5 · 9 = 45

2) 9 ∙ 9 = 81

2 1
18 + 54 : 9 = 24

1) 54 : 9 = 6, так как 6 · 9 = 54

) 18 + 6 = 18 + (2 + 4) = (18 + 2) + 4 = 20 + 4 = 24

Представим число 6 в виде суммы чисел 2 и 4. Вначале к числу 18 прибавим число 2, а потом прибавим число 4.

1 2
34 : 4 · 8 = 64

1) 32 : 4 = 8, так как 4 · 8 = 32

2) 8 ∙ 8 = 64

Шаг 4.
Оформляем задание в тетрадь.

64 : 8 = 8
72 : 9 = 8
81 : 9 = 9
56 : 8 = 7

7 ∙ 7 = 49
8 ∙ 8 = 64
9 ∙ 9 = 81
6 ∙ 6 = 36

(36 – 28) · 5 = 8 · 5 = 40
4 · (23 – 16) = 4 · 7 = 28
(32 – 27) · 6 = 5 · 6 = 30
5 · (64 – 60) = 5 · 4 = 20

36 + (24 : 6) = 36 + 4 = 40
45 : 5 · 9 = 5 · 9 = 45
18 + 54 : 9 = 18 + 6 = 24
32 : 4 · 8 = 8 · 8 = 64

Номер 2.

Девочка принесла для кроликов 27 морковок, а мальчик – 18 морковок. Все морковки они разложили кроликам в клетки, по 9 морковок в каждую. Объясни, что означают выражения:

27 : 9 18 : 9 27 + 18 (27 + 18) : 9

Ответ:

27 : 9 – в такое количество клеток разложила девочка морковь. 18 : 9 – в такое количество клеток разложил мальчика морковь. 27 + 18 – всего морковок было у детей. (27 + 18) : 9 – во сколько клеток была разложена морковь.

Подсказка:

Данная задача: вида «кол-во морковок в клетке, кол-во клеток, общее кол-во морковок» характеризуется зависимостями между компонентами:

Кол-во морковок в 1 клетке · кол-во клеток = общее кол-во морковок.
Общее кол-во морковок : кол-во клеток = кол-во морковок в 1 клетке.
Общее кол-во морковок : кол-во морковок в 1 клетке : кол-во клеток.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Девочка принесла 27 морковок, а мальчик – 18. Их они раскладывали в ящики по 9 морковок в каждый. Мы знаем, сколько морковок всего было у каждого, знаем, сколько морковок было в каждом ящике, но нам неизвестно, сколько ящиков было.
Чтобы это узнать, нужно общее количество морковок у каждого разделить на количество моркови в каждой клетке.

27 : 9 = 3 (кл.) – в такое количество клеток разложила девочка морковь.

18 : 9 = 2 (кл.) – в такое количество клеток разложил мальчика морковь.

Шаг 3.
Продолжаем рассуждение.

Общее количество морковок детей складывается из количества морковок девочек и мальчиков. Значит, чтобы узнать, сколько морковок было всего, нужно сложить количество морковок мальчиков и девочек.

27 + 18 = 45 (шт.) – количества моркови у детей.

Шаг 4.
Продолжаем рассуждение.

Мы узнали, что у детей всего было 45 морковок. Они разложили их по 9 морковок в клетку. Значит, нам известно общее количество морковок, количество морковок в клетке, но неизвестно количество клеток. При этом, количество моркови в клетках одинаковое.
Поэтому, чтобы узнать, сколько клеток было, нужно общее количество моркови разделить на количество морковок в 1 клетке.

(27 + 18) : 9 = 45 : 9 = 5 (кл.) – во сколько клеток была разложена морковь.

Шаг 5.
Оформляем задание в тетрадь.

27 : 9 = 3 (шт.) – Выражение для вычисления количества клеток с морковками девочки.

18 : 9 = 2 (шт.) – Выражение для вычисления количества клеток с морковками мальчиков.

27 + 18 = 45 (шт.) – Выражение для вычисления общее количество морковок.

(27 + 18) : 9 = 5 (шт.) – Выражение для вычисления количества клеток.

Номер 3.

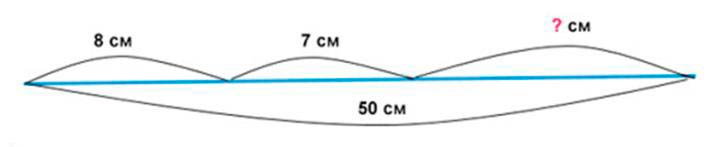
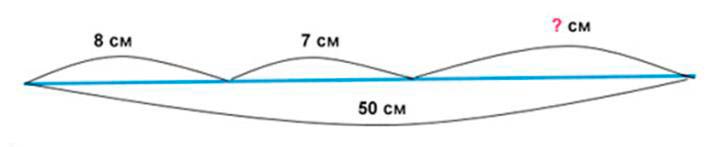
Длина провода 50 м. Сначала от него отрезали 8 м, потом 7 м. Сколько метров провода осталось?
Реши задачу разными способами.

Ответ:

Было – 50 м Отрезали сначала – 8 м Отрезали потом – 7 м Осталось – ? м
1-й способ решения: 1) 50 − 8 = 42 (м) – осталось, когда отрезали первый раз. 2) 42 − 7 = 35 (м) – осталось провода. Ответ: 35 метров провода осталось всего .
2-й способ решения: 1) 8 + 7 = 15 (м) – всего отрезали. 2) 50 − 15 = 35 (м) – провода осталось. Ответ: 35 метров провода осталось всего.

Подсказка:

Решение задачи сводится к выражению, основанном на правиле вычитания суммы из числа: а – (в + с) = (а – в) – с.

Способ решения 1.

Шаг 1.
Оформляем условие в виде рисунка или краткой записи.

Было – 50 м
Отрезали сначала – 8 м
Отрезали потом – 7 м
Осталось – ? м

Шаг 2.
Рассуждаем.

Сначала от провода отрезали 8 метров, а потом еще 7 метров. Общее количество отрезанного провода складывается из длины первого куска и второго куска. Значит, чтобы узнать, сколько метров провода отрезали всего, нужно сложить длины проводов.

8 + 7 = 15 (м) – всего отрезали.

Шаг 3.
Продолжаем рассуждение.

Общая длина провода складывается из длины отрезанной части и оставшейся. Значит, чтобы узнать, сколько метров провода осталось, нужно из общей длины провода вычесть длину отрезанной.

50 − 15 = 35 (м) – провода осталось.

Шаг 4.
Записываем ответ.

Ответ: 35 м провода осталось.

Решение выражением:
50 – (8 + 7) = 35 (м), где 8 + 7 – длина отрезанных частей, основанном на правиле вычитания суммы из числа.

Способ решения 2.

Шаг 1.
Оформляем условие в виде рисунка или краткой записи.

Было – 50 м
Отрезали сначала – 8 м
Отрезали потом – 7 м
Осталось – ? м

Шаг 2.
Рассуждаем.

Изначально было 50 м ткани. Сначала от провода отрезали 8 м. Сколько осталось провода после первого отреза можно узнать, если из общей длины провода вычесть длину, которые отрезали сначала.

50 – 8 = 42 (м) – осталось, когда отрезали первый раз.

Шаг 3.
Продолжаем рассуждение.

Теперь длина провода складывается из длины, которую нужно отрезать во второй раз и оставшейся части. Значит, чтобы узнать, сколько метров провода осталось, нужно из оставшейся длины провода вычесть длину, которую отрезали во второй раз.

42 − 7 = 35 (м) – осталось провода.

Шаг 4.
Записываем ответ.

Ответ: 35 м провода осталось.

Номер 4.

Ответ:

3 м 9 дм = 39 дм 56 см = 5 дм 6 см 4 см 8 мм = 48 мм 25 мм = 2 см 5 мм

Подсказка:

Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм

Шаг 1.
Рассмотрим выражения.

3 м 9 дм = 30 дм + 9 дм = 39 дм,
так как 1 м = 10 дм

4 см 8 мм = 40 мм + 8 мм = 48 мм,
так как 1 см = 10 мм

56 см = 50 см + 6 см = 5 дм 6 см,
так как 10 см = 1 дм

25 мм = 20 мм + 5 мм = 2 см 5 мм,
так как 1 см = 10 мм

Шаг 2.
Оформляем задание в тетрадь.

3 м 9 дм = 39 дм
4 см 8 мм = 48 мм
56 см = 5 дм 6 см
25 мм = 2 см 5 мм

Номер 5.

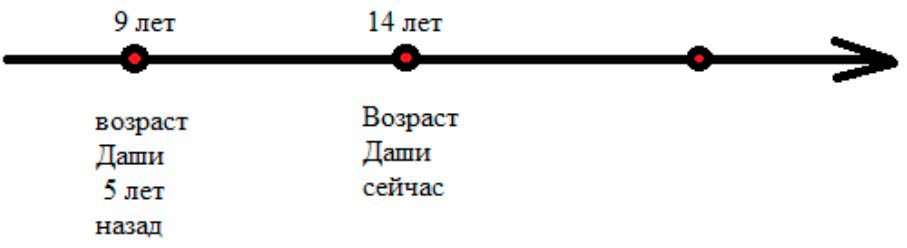
Даше 14 лет, а Оле 8 лет. Сколько лет было Оле, когда Даше было 9 лет?

Ответ:

Даша - 14 лет Оля - 8 лет Даша - 9 лет Оля - ? лет

1-й способ решения: 1) 14 − 8 = 6 (л.) – на столько Даша старше Оли. 2) 9 − 6 = 3 (г.) – было Оле. Ответ: 3 года было Оле, когда Даше было 9 лет.

2-й способ решения: 1) 14 – 9 = 5 (л) – сколько лет назад Даше было 9 лет. 2) 8 – 5 = 3 (г) – было Оле 9 лет назад или, когда Даше было 9 лет. Ответ: 3 года.

Подсказка:

Попытайся расположить возрасты девочек на прямой, отметив конкретный возраст точками.

Шаг 1.
Оформляем условие в виде рисунка.

Шаг 2.
Рассуждаем.

Сейчас Даше 14 лет. Нужно узнать, сколько лет назад Даше было 9 лет. Для этого, из возраста, который у неё сейчас, нужно вычесть возраст, который был.

14 лет – 9 лет = 5 лет.
Значит, 5 лет назад Даше было 9 лет.

Шаг 3.
Продолжаем рассуждение.

Если Даше 5 лет назад было 9 лет, то чтобы узнать, сколько лет было Оле, когда Дашей было 9, нужно из возраста Оли вычесть 5 лет.

8 лет – 5 лет = 3 года.
Значит, когда Даше было 9 лет, Оле было 3 года.

Шаг 4.
Записываем ответ.

Ответ: Оле было 3 года.

Номер 6.

Найди площадь и периметр квадрата, если длина его стороны 7 см; если длина его стороны 4 см; если длина его стороны 9 см.

Ответ:

Площади квадратов: 1) 7 ∙ 7 = 49 см² 2) 4 ∙ 4 = 16 см² 3) 9 ∙ 9 = 81 см²
Периметры квадратов: 1) 7 ∙ 4 = 28 см 2) 4 ∙ 4 = 16 см 3) 9 ∙ 4 = 36 см
Площадь прямоугольника равна произведению его длины и ширины. Периметр многоугольника – это сумма длин всех его сторон.

Подсказка:

1) Площадь фигуры измеряется в квадратных сантиметрах (см²).

2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Рассмотрим квадрат со стороной 7 см.

Шаг 1.
Рассуждаем.

Способ 1: сложить все стороны.
7 + 7 + 7 + 7 = 28 (см)

Споосб 2: так как все стороны у квадрата равны, то чтобы найти периметр квадрата можно строну квадрата умножить на 4.

7 · 4 = 28 (см)

Шаг 2.
Продолжаем рассуждение.

У квадрата длина и ширина равны. Значит для того чтобы вычислить площадь квадрата нужно сторону квадрата умножить два раза.

7 · 7 = 49 (см²) – площадь прямоугольника.

Шаг 3.
Записываем ответ.

Ответ: 49 см² площадь, 28 см – периметр.

Рассмотрим квадрат со стороной 4 см.

Шаг 1.
Рассуждаем.

Способ 1: сложить все стороны.
4 + 4 + 4 + 4 = 16 (см)

Споосб 2: так как все стороны у квадрата равны, то чтобы найти периметр квадрата можно строну квадрата умножить на 4.

4 · 4 = 16 (см)

Шаг 2.
Продолжаем рассуждение.

У квадрата длина и ширина равны. Значит для того чтобы вычислить площадь квадрата нужно сторону квадрата умножить два раза.

4 · 4 = 16 (см²) – площадь прямоугольника.

Шаг 3.
Записываем ответ.

Ответ: 16 см² площадь, 16 см – периметр.

Рассмотрим квадрат со стороной 9 см.

Шаг 1.
Рассуждаем.

Способ 1: сложить все стороны.
9 + 9 + 9 + 9 = 36 (см)

Споосб 2: так как все стороны у квадрата равны, то чтобы найти периметр квадрата можно строну квадрата умножить на 4.

9 · 4 = 36 (см)

Шаг 2.
Продолжаем рассуждение.

У квадрата длина и ширина равны. Значит для того чтобы вычислить площадь квадрата нужно сторону квадрата умножить два раза.

9 · 9 = 81 (см²) – площадь прямоугольника.

Шаг 3.
Записываем ответ.

Ответ: 81 см² площадь, 36 см - периметр.

Шаг 4.
Оформляем задание в тетрадь.

7 + 7 + 7 + 7 = 7 ∙ 4 = 28 (см) − периметр квадрата со стороной 7 см.

7 ∙ 7 = 49 (см²) − площадь квадрата со стороной 7 см.

4 + 4 + 4 + 4 = 4 ∙ 4 = 16 (см) − периметр квадрата со стороной 4 см.

4 ∙ 4 = 16 (см²) − площадь квадрата со стороной 4 см.

9 + 9 + 9 + 9 = 9 ∙ 4 = 36 (см) − периметр квадрата со стороной 9 см.

9 ∙ 9 = 81 (см²) − площадь квадрата со стороной 9 см.

Задание внизу страницы

Ответ:

Подсказка:

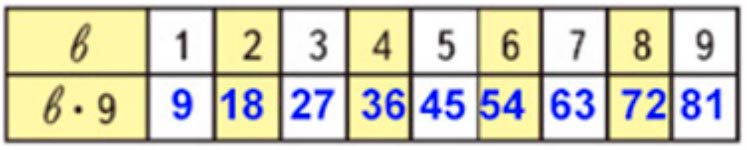
b · 9, значит, умножить на 9, т.е. увеличить число в 9 раз.

Шаг 1.
Промежуточные вычисления.

b · 9, если:

b = 1, то 1 · 9 = 9,
где 1 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 2, то 2 · 9 = 18,
где 2 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 3, то 3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 4, то 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 5, то 5 · 9 = 45,
где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 6, то 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 7, то 7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 8, то 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

b = 9, то 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

Шаг 2.
Заполним таблицу.

Задание на полях страницы

Вычисли. Найди лишнее выражение:

Ответ:

40 : 5 = 8 64 : 8 = 8 32 : 4 = 8 72 : 9 = 8 80 : 10 = 8 56 : 7 = 8 48 : 6 = 8 24 : 4 = 6 – лишнее выражение. Ответ: лишнее выражение 24 : 4, потому что значение выражения 6, а остальных - 8.

Подсказка:

Чтобы понять, какое выражение лишнее, нужно рассмотреть все: из каких компонентов состоит, на каких арифметических действиях основано, каково их значение

Шаг 1.
Вычислим значения выражений и сравним их.

40 : 5 = 8, так как 5 · 8 = 40,
где 5 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

64 : 8 = 8, так как 8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

32 : 4 = 8, так как 4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

24 : 4 = 6, так как 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

72 : 9 = 8, так как 9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

80 : 10 = 8, так как 8 · 10 = 80,
где 8 – одинаковое слагаемое, а 10 – количество одинаковых слагаемых.

56 : 7 = 8, так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

48 : 6 = 8, так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

Шаг 2.
Делаем вывод.

Вывод: лишнее выражение – 24 : 4 = 6, потому что значение этого равенства отличается от значений других выражений, в остальных примерах частное равно 8.

Шаг 3.
Записываем ответ.

Ответ: выражение 24 : 4 = 6 – лишнее.

математика 3 класс Моро 1 часть страница 65. Год 2023

Учимся решать задачи и выполнять вычисления.

Номер 1.

За три дня рабочие отремонтировали 24 троллейбуса: в первый день 8 троллейбусов, во второй 10. Сколько троллейбусов они отремонтировали в третий день? Рассмотри схематический чертёж и реши задачу.

Ответ:

24 – (8 + 10) = 6 (т.)
Проверка: 8 + 10 + 6 = 24 (т.) Ответ: в третий день отремонтировали 6 троллейбусов.

Подсказка:

Решение задачи сводится к выражению, основанном на правиле вычитания суммы из числа: а – (в + с) = (а – в) – с.

Шаг 1.
Оформляем условие в виде схематического чертежа.

Шаг 2.
Рассуждаем.

Общее количество отремонтированных за два дня троллейбусов складывается из количества отремонтированных троллейбусов за первый и второй день. Поэтому, чтобы узнать, сколько троллейбусов отремонтировали за 2 дня, нужно сложить количество отремонтированного транспорта в каждый из дней.

8 + 10 = 18 (тр.) – отремонтировали за два дня.

Шаг 3.
Продолжаем рассуждение.

Общее количество отремонтированного транспорта складывается из транспорта, отремонтированного за два дня и третий. Соответственно, чтобы узнать, сколько машин отремонтировали за третий день, нужно из общего количества троллейбусов вычесть те, что были отремонтированы за два первых дня.

24 – 18 = 6 (тр.) – отремонтировали в 3 день.

Шаг 4.
Записываем ответ.

Ответ: в третий день отремонтировали 6 троллейбусов.

Шаг 5.
Сделаем проверку.

Чтобы сделать проверку нужно узнать общее количество отремонтированных автобусов за 3 дня.

8 + 10 + 6 = 24 (тр.) – всего отремонтировали.

24 = 24 – задача решена верно.

Номер 2.

Выполни задания по таблице на обороте обложки учебника.

Найди произведение: 4 · 7; 7 · 9; 8 · 6; 2 · 9.
Проверь, что 6 · 7 = 7 · 6; 8 · 9 = 9 · 8.
Найди частное: 28 : 7; 24 : 6; 63 : 7; 45 : 9.
Назови числа от 7 до 63, которые делятся на 7.
Назови числа от 9 до 81, которые делятся на 9.
Объясни, как получены из чисел первой строки числа восьмой строки; девятой строки.

Ответ:

1) 4 ∙ 7 = 28 7 ∙ 9 = 63 8 ∙ 6 = 48 2 ∙ 9 = 18
2) 6 ∙ 7 = 7 ∙ 6 8 ∙ 9 = 9 ∙ 8 42 = 42 72 = 72
3) 28 : 7 = 4 24 : 6 = 4 63 : 7 = 9 45 : 9 = 5
4) 7, 14, 21, 28, 35, 42, 56, 63
5) 9, 18, 27, 36, 45, 54, 63, 72, 81
6) В 8 строке все числа первой строки умножали на 8. В 9 строке все числа первой строки умножили на 9.

Подсказка:

Для выполнения задания обращайся к таблице умножения и деления чисел от 1 до 9.

Шаг 1.
Найдём произведение.

Произведение, значит, нужно найти числа, стоящие на пересечении 4 и 7, 7 и 9, 8 и 6, 2 и 9.

4 · 7 = 28, где 4 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

8 · 6 = 48, где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

2 · 9 = 18, где 2 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

Шаг 2.
Проверим равенства.

Помни о существующем переместительном свойстве умножения.

Сравним выражения 6 · 7 и 7 · 6.

6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

7 · 6 = 42, где 7 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

42 = 42, значит, 6 · 7 = 7 · 6
По переместительному свойству умножения.

8 · 9 и 9 · 8
8 · 9 = 72, это по 8 – 9 раз, где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 8 = 72, это по 9 – 8 раз, где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
72 = 72, значит, 8 · 9 = 9 · 8

Шаг 3.
Найдём частное.

Частное – это результат деления.

28 : 7 = 4, так как 7 · 4 = 28,
где 7 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

24 : 6 = 4, так как 6 · 4= 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

63 : 7 = 9, так как 7 · 9 = 63,
где7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

45 : 9 = 5, так как 9 · 5 = 45,
где 9 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

Шаг 4.
Рассуждаем.

Делятся на 7, значит, являются результатом таблицы умножения и деления 7.

Значит, выписываю числа: 7, 14, 21, 28, 35, 42, 49, 56, 63.

Шаг 5.
Продолжаем рассуждение.

Делятся на 9, значит, являются результатом таблицы умножения и деления 9.

Значит, выписываю числа: 9, 18, 27, 36, 45, 54, 63, 72, 81.

Шаг 6.
Продолжаем рассуждение.

Помни, что таблицы на обороте – таблицы умножения.
Значит, числа восьмой и девятой строки получены умножением на какое – либо число.

Числа восьмой строки – таблица умножения 8. Получены умножением чисел первого ряда на 8.

Числа девятой строки – таблица умножения 9.
Получены умножения чисел первого ряда на 9.

Шаг 7.
Оформляем задание в тетрадь.

1)
4 ∙ 7 = 28
7 ∙ 9 = 63
8 ∙ 6 = 48
2 ∙ 9 = 18

2)
6 ∙ 7 = 7 ∙ 6
6 ∙ 7 = 42
7 ∙ 6 = 42 8 ∙ 9 = 9 ∙ 8
8 ∙ 9 = 72
9 ∙ 8 = 72

3)
28 : 7 = 4
24 : 6 = 4
63 : 7 = 9
45 : 9 = 5

4) 7, 14, 21, 28, 35, 42, 56, 63
5) 9, 18, 27, 36, 45, 54, 63, 72, 81
6) В 8 строке все числа первой строки умножали на 8.
В 9 строке все числа первой строки умножили на 9.

Номер 3.

82 – 36 : 4 40 – 15 : 5 + 10 7 · (12 – 4) 52 + 27 : 3 40 – 15 : (5 + 10) 8 · (25 – 20) 94 + 24 : 4 (40 – 15) : 5 + 10 18 : (11 – 9)

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 65. Номер 3

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.

4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.

Шаг 1.
Расставляем порядок действий.

2 1
82 − 36 : 4 = 73
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом вычитание.

2 1
52 + 27 : 3 = 61
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.

2 1
94 + 24 : 4 = 100
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.

2 1 3
40 − 15 : 5 + 10 = 47
В данном выражении присутствуют действия сложение, вычитание и деление. Вначале выполним действие деление. потом вычитание и третим действием – сложение.

3 2 1
40 − 15 : (5 + 10) = 39
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и третьим действием – вычитание.

1 2 3
(40 − 15) : 5 + 10 = 15
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и третьим действием – сложение.

2 1
7 · (12 − 4) = 56
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом вычитание.

2 1
8 · (25 − 20) = 40
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом вычитание.

2 1
18 : (11 − 9) = 9
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом вычитание.

Шаг 2.
Выполняем вычисления по действиям.

2 1
82 − 36 : 4 = 73
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом вычитание.
1) 36 : 4 = 9
2) 82 − 9 = 73

2 1
52 + 27 : 3 = 61
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.
1) 27 : 3 = 9
2) 52 + 9 = 61

2 1
94 + 24 : 4 = 100
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.
1) 24 : 4 = 6
2) 94 + 6 = 100

2 1
7 · (12 − 4) = 56
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом вычитание.
1) 12 – 4 = 8
2) 7 ∙ 8 = 56

2 1
8 · (25 − 20) = 40
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом вычитание.
1) 25 – 20 = 5
2) 8 ∙ 5 = 40

2 1
18 : (11 − 9) = 9
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом вычитание.
1) 11 – 9 = 2
2) 18 : 2 = 9

Шаг 3.
Оформляем задание в тетрадь.

82 – 36 : 4 = 82 – 9 = 73
52 + 27 : 3 = 52 + 9 = 61
94 + 24 : 4 = 94 + 6 = 100

40 – 15 : 5 + 10 = 40 – 3 + 10 = 37 + 10 = 47

40 – 15 : (5 + 10) = 40 – 15 : 15 = 40 – 1 = 39

(40 − 15) : 5 + 10 = 25 : 5 + 10 = 5 + 10 = 15

7 · (12 – 4) = 7 · 8 = 56
8 · (25 – 20) = 8 · 5 = 40
18 : (11 – 9) = 18 : 2 = 9

Задание в низу страницы.

Ребята сделали 10 красных фонариков и 6 жёлтых. Они собрали гирлянды, по 8 фонариков в каждой. Сколько получилось гирлянд?

Ответ:

(10 + 6) : 8 = 2 (г.) Ответ: получилось 2 гирлянды.

Подсказка:

Данная задача: вида «кол-во в 1 гирлянде, количество гирлянд, общее количество фонариков» характеризуется зависимостями между компонентами:

Кол-во фонариков в 1 гирлянде · кол-во гирлянд = общее кол-во фонариков.
Общее кол-во фонариков : кол-во гирлянд = кол-во фонариков в 1 гирлянде.
Общее кол-во фонариков : кол-во фонариков в 1 гирлянде = кол-во гирлянд.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Общее количество подвешенного на гирлянде складывается из количества красных фонариков и желтых. Значит, чтобы узнать, сколько всего фонариков было в гирлянде, нужно сложить количество красных и желтых фонариков.

10 + 6 = 16 (шт.) – всего фонариков.

Шаг 3.
Продолжаем рассуждение.

Мы узнали, что всего было 16 фонариков. Их развесили на гирлянды, по 8 штук на каждую. Нам неизвестно, сколько гирлянд получилось. Из таблицы видно, что чтобы узнать, сколько гирлянд получилось, нужно общее количество фонариков разделить на количество фонариков на 1 гирлянде.

16 : 8 = 2 (шт.) - получилось гирлянд.

Шаг 4.
Записываем ответ.

Ответ: получилось 2 гирлянды.

Решение выражением:
(10 + 6) : 8 = 2 (гир.), где 10 + 6 – количество сделанных детьми фонариков.

Задание на полях страницы.

Ответ:

Пояснение:
Первая занимательная рамка:
26 + 34 + 40 = 60 + 40 = 100
40 + 6 + 54 = 40 + 60 = 100
26 + 54 + 20 = 80 + 20 = 100

Вторая занимательная рамка:
40 + 25 + 15 = 40 + 40 = 80
15 + 35 + 30 = 50 + 30 = 80
40 + 10 + 30 = 40 + 40 = 80