Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 47

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Сравни задачи, сравни их решения.
1) В мастерской изготовили 40 больших столов, а маленьких в 8 раз меньше, чем больших. Сколько всего столов изготовили?
2) В мастерской изготовили 40 больших столов, а маленьких на 8 меньше, чем больших. Сколько всего столов изготовили?
Задача 1:

1) 40 : 8 = 5 (ст.) – маленьких изготовили.
2) 40 + 5 = 45 (ст.)
Ответ: 45 столов изготовили всего.
Задача 2:

1) 40 − 8 = 32 (ст.) – маленьких изготовили.
2) 40 + 32 = 72 (ст.)
Ответ: 72 стола изготовили всего.
Задачи похожи сюжетом и тем, что нужно найти, сколько всего столов. Отличаются задачи тем, что в первой при сравнении количества больших и маленьких столов говорится «в 8 раз меньше», а во второй – «на 8 столов меньше». Поэтому и первое действие отличается.
1) «в 8 раз меньше», значит, вычисляется делением.
2) «на 8 меньше», значит, вычисляется вычитанием.
Оформляем условие в виде краткой записи.
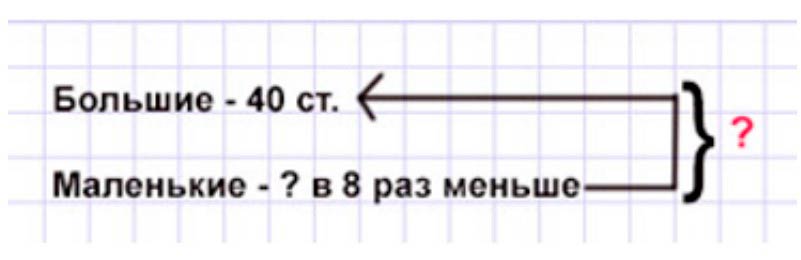
Рассуждаем.
В мастерской изготовили 40 больших столов, а маленьких – в 8 раз меньше. Соответственно, чтобы узнать, сколько маленьких столов изготовили, нужно количество больших столов разделить на 8.
40 : 8 = 5 (ст.) – изготовили маленьких.
Продолжаем рассуждение.
Общее количество столов сена складывается из количества больших и маленьких столов. Значит, чтобы узнать, сколько столов всего, нужно сложить количество больших и маленьких столов.
40 + 5 = 45 (ст.) – всего изготовили.
Запишем ответ.
Ответ: 45 столов.
Решение выражением:
40 + 40 : 8 = 45 (ст.).
Оформляем условие в виде краткой записи.
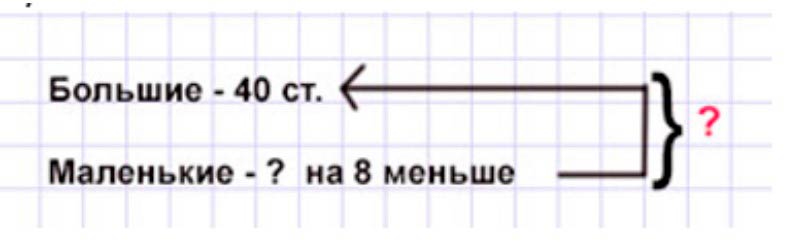
Рассуждаем.
В мастерской изготовили 40 больших столов, а маленьких – на 8 меньше. На 8 меньше, значит, столько же, сколько больших столов, но без 8 столов. Поэтому, чтобы узнать, сколько маленьких столов израсходовали, нужно из количества больших столов вычесть 8 столов.
40 – 8 = 32 (ст.) – изготовили маленьких.
Продолжаем рассуждение.
Общее количество столов сена складывается из количества больших и маленьких столов. Значит, чтобы узнать, сколько столов всего, нужно сложить количество больших и маленьких столов.
40 + 32 = 72 (ст.) – всего изготовили.
Запишем ответ.
Ответ: 72 стола.
Решение выражением:
40 + (40 - 32) = 72 (ст.).
Сравниваем задачи.
Задачи похожи сюжетом и тем, что нужно найти.
Задачи отличаются действием. В первой задаче сказано «во сколько раз меньше» — решается действием деление, а во второй сказано «на сколько меньше» — это решается вычитание.
Номер 2.
Составь задачи по выражениям.
1) 8 + 8 ∙ 2 2) 8 + (8 + 2)
Ответ:Задача 1: В ателье сшили 8 платьев, а блузок сшили в 2 раза больше. Сколько сшили всего платьев и блузок?

Ответ: 24 платья и блузки было сшито всего.
Задача 2: В ателье сшили 8 платьев, а блузок на 2 больше, чем платьев. Сколько сшили платьев и блузок всего?

Ответ: 18 штук блузок и платьев сшили всего.
1) «в 2 раза больше», значит, вычисляется умножением.
2) «на 2 больше», значит, вычисляется сложением.
Составим задачу.
В ателье сшили 8 платьев, а блузок сшили в 2 раза больше. Сколько сшили всего платьев и блузок?
Оформляем условие в виде краткой записи.
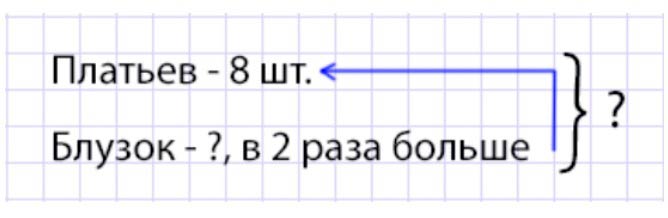
Рассуждаем.
В ателье сшили 8 платьев, а блузок – в 2 раза больше. Значит, что блузок сшили два раза по количеству платьев. Поэтому, чтобы узнать, сколько блузок сшили, нужно количество платьев умножить на 2.
8 · 2 = 16 (шт.) – сшили блузок.
Продолжаем рассуждение.
Общее количество сшитых вещей складывается из количества платьев и блузок. Поэтому, чтобы узнать сколько одежды сшили, нужно сложить количество платьев и блузок.
8 + 16 = 24 (шт.) – сшили платьев и блузок вместе.
Запишем ответ.
Ответ: 24 платьев и блузок.
Решение выражением:
8 + 8 · 2 = 24 шт.
Составим задачу.
В ателье сшили 8 платьев, а блузок на 2 больше, чем платьев. Сколько сшили платьев и блузок всего?
Оформляем условие в виде краткой записи.
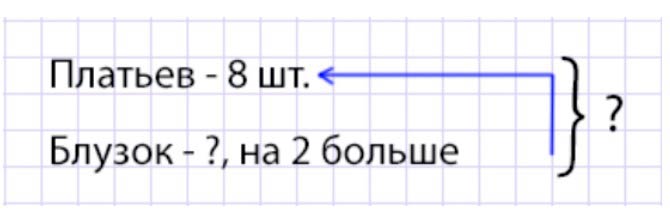
Рассуждаем.
В ателье сшили 8 платьев, а блузок – на 2 больше. Соответственно, что блузок сшили столько, сколько платьев и еще 2 платья. Поэтому, чтобы узнать, сколько блузок сшили, нужно к количеству платьев прибавить 2 платья.
8 + 2 = 10 (шт.) – сшили блузок.
Продолжаем рассуждение.
Общее количество сшитых вещей складывается из количества платьев и блузок. Поэтому, чтобы узнать сколько одежды сшили, нужно сложить количество платьев и блузок.
8 + 10 = 18 (шт.) - сшили платьев и блузок вместе.
Запишем ответ.
Ответ: 18 платьев и блузок.
Решение выражением:
8 + (8 + 2) = 18шт.
Номер 3.
Масса кабачка 2 кг, а масса тыквы в 6 раз больше. Чему равна масса кабачка и тыквы вместе?
Ответ:

1-й способ решения:
1) 2 ∙ 6 = 12 (кг) – масса тыквы.
2) 2 + 12 = 14 (кг)
Ответ: 14 кг масса тыквы и кабачка.
2-й способ решения: 2 + 2 ∙ 6 = 2 + 12 = 14 (кг) – масса тыквы и кабачка. Ответ: 14 кг.
1) «в 6 раз больше», значит, вычисляется умножением. 2) «всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.
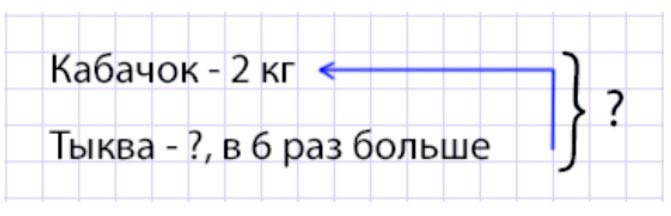
Рассуждаем.
Масса кабачка – 2 кг, а тыквы – в 6 раз больше. В 6 раз больше, значит, по 2 – 6 раз. Чтобы узнать, какова масса тыквы, нужно массу кабачка умножить на 6.
2 · 6 = 12 (кг) – масса тыквы.
Продолжаем рассуждение.
Общая масса овощей складывается из массы кабачка и тыквы. Значит, чтобы узнать массу овощей, нужно сложить массу кабачка и тыквы.
2 + 12 = 14 (кг) – масса кабачка и тыквы.
Запишем ответ.
Ответ: 14 кг.
Решение выражением:
2 + 2 · 6 = 14 (кг)
Номер 4.
Ответ:6 ∙ 9 = 54 36 : 6 = 6

27 : 9 = 3 24 : 4 = 6
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6.
Рассуждаем и выполняем вычисления.
6 · 9 = 54
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 6 = 6
так как 6 · 6 = 36
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
1 2
(50 – 38) : 4 = 3
1) 50 – 38 = (40 + 10) – (30 + 8) = (40 – 30) + (10 – 8) = 10 + 2 = 12
2) 12 : 4 = 3
так как 3 · 4 = 12
В выражении присутствуют действия вычитание и сложение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом вне скобок – деление.
27 : 9 = 3
так как 3 · 9 = 27
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
24 : 4 = 6
так как 4 · 6 = 24
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
6 ∙ 9 = 54
36 : 6 = 6
(50 − 38) : 4 = 12 : 3 = 3
27 : 9 = 3
24 : 4 = 6
Номер 5.
Ответ:
1) с : 6, значит, уменьшить число С в 6 раз, т.е разделить.
2) Для выполнения задания обращайся к таблице умножения и деления с числом 6.
Промежуточные вычисления.
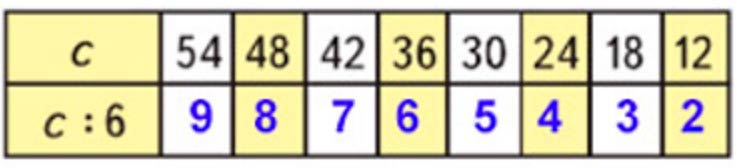
54 : 6 = 9
так как 6 · 9 = 54
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
48 : 6 = 8
так как 6 · 8 = 48
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
42 : 6 = 7
так как 6 · 7 = 42
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
36 : 6 = 6
так как 6 · 6 = 36
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
30 : 6 = 5
так как 6 · 5 = 30
где 6 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
24 : 6 = 4
так как 6 · 4 = 24
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
18 : 6 = 3
так как 6 · 3 = 18
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
12 : 6 = 2
так как 6 · 2 = 12
где 6 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
Заполним таблицу.
Номер 6.
Реши уравнения. Сделай проверку.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения.
Рассмотрим уравнения.
23 + х = 31
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
k – 17 = 33
k – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
45 – а = 9
а – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
Решим уравнение.
23 + x = 31
x = 31 − 23
x = 8
k − 17 = 33
k = 33 + 17
k = 50
45 − a = 9
a = 45 − 9
a = 36
Выполняем проверку.
23 + x = 31
Проверка: в уравнение вместо неизвестного х подставим число 8.
23 + 8 = 23 + (7 + 1) = (23 + 7) + 1 = 30 + 1 = 31
31 = 31 – верно.
k − 17 = 33
Проверка: в уравнение вместо неизвестного k подставим число 50.
50 − 17 = (40 + 10) – (10 + 7) = (40 – 10) + (10 – 7) = 30 + 3 = 33
33 = 33 - верно.
45 − a = 9
Проверка: В уравнение вместо неизвестного a подставим число 36.
45 − 36 = 45 + (35 + 1) = (45 – 35) – 1 = 10 – 1 = 9
9 = 9 – верно.
Оформляем задание в тетрадь.
23 + x = 31
x = 31 − 23
x = 8
Проверка:
23 + 8 = 31
31 = 31
k − 17 = 33
k = 33 + 17
k = 50
Проверка:
50 − 17 = 33
33 = 33
45 − a = 9
a = 45 − 9
a = 36
Проверка:
45 − 36 = 9
9 = 9
Номер 7.
Подсчитай разными способами, на сколько одинаковых квадратов (клеток) разбита каждая фигура. В какой из них поместилось больше квадратов?

1-й способ решения:
1) 3 ∙ 3 + 2 ∙ 6 = 21 (кл.) – в красной ф.
2) 2 ∙ 7 + 1 ∙ 5 = 19 (кл.) – в голубой ф.
2-й способ решения:
1) 2 ∙ 9 + 3 = 21 (кл.) – в красной ф.
2) 3 ∙ 5 + 4 = 19 (кл.) – в голубой ф.
Ответ: больше квадратов (клеток) поместилось в красной фигуре.
Помни о том, что умножение – замена одинаковых слагаемых произведением,
где а · 3,
а – первый множитель,
3 – количество множителей.
Первый способ.
Посчитаем количество квадратов:
Розовая фигура – 21 квадрат.
Голубая фигура – 19 квадратов.
Второй способ.
Посчитаем по линиям:
Розовая фигура: две линии по 9 квадратов и одна линия в 3 квадрата.
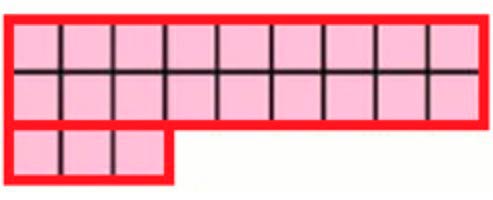
9 + 9 + 3 = 18 + 3 = 21 (кв.).
Также одинаковые слагаемые можем заменить умножением:
9 ∙ 2 + 3 = 18 + 3 = 21 (кв.) – в розовой фигуре.
Синяя фигура: одна линия в 5 квадратов и две линии по 7 квадратов.
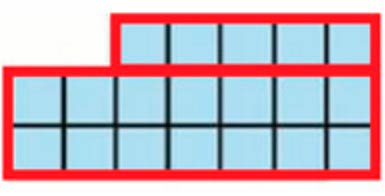
5 + 7 + 7 = 12 + 7 = 19 (кв.).
Также одинаковые слагаемые можем заменить умножением:
5 + 2 ∙ 7 = 5 + 14 = 19 (кв.) – в синей фигуре.
Третий способ.
Разобьем фигуры на несколько фигур, умножим число рядов на число столбцов в каждой из них и сложим результаты:
Розовая фигура состоит из трёх строк по 3 квадрата и двух строк по 6 квадратов.
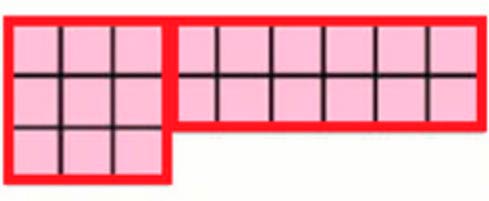
3 + 3 + 3 + 6 + 6 = 9 + 12 = 21 (кв.).
Также одинаковые слагаемые можем заменить умножением:
3 ∙ 3 + 2 ∙ 6 = 9 + 12 = 21 (кв.) – в розовой фигуре.
Голубая фигура состоит из двух строк по 2 квадрата и трёх строк по 5 квадратов.

2 + 2 + 5 + 5 + 5 = 4 + 15 = 19 (кв.).
Также одинаковые слагаемые можем заменить умножением:
2 ∙ 2 + 3 ∙ 5 = 4 + 15 = 19 (кв.) – в голубой фигуре.
Сравним фигуры.
В розовой фигуре – 21 квадрат. В синей голубой фигуре – 19 квадратов.
21 > 19, значит в розовой фигуре больше квадратов, чем в голубой фигуре.
Ответ: в розовой фигуре больше.
Номер 8.
В большой клетке попугаев в 2 раза больше, чем в маленькой, а в маленькой на 5 попугаев меньше, чем в большой. Сколько попугаев в большой клетке?
Ответ:

5 ∙ 2 = 10 (п.)
Ответ: 10 попугаев в большой клетке.
1) «в 2 раза больше», значит, вычисляется умножением.
2) «на 5 попугаев меньше», значит, вычисляется вычитанием.
Оформляем условие в виде схемы.
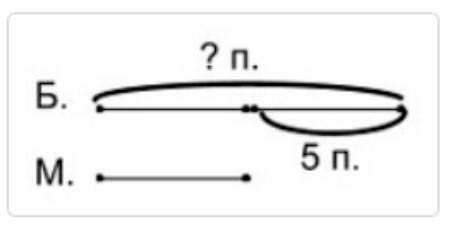
Рассуждаем.
В большой клетке попугаев в 2 раза больше, чем в маленькой.
В маленькой клетке на 5 попугаев меньше, чем в большой. Значит, что в большой клетке на 5 попугаев больше.
Соответственно, 5 попугаев – это и есть половина количества попугаев большой клетки.
5 · 2 = 10 (п.) – в большой клетке.
Сделаем проверку.
Проверяем: 10 попугаев в большой клетке в 2 раза больше, чем 5 попугаев в маленькой клетке, потому что 10 : 5 = 2.
И 10 попугаев в большой клетке на 5 попугаев больше, чем в маленькой, т.к. 10 – 5 = 5 попугаев.
Задача решена, верно.
Записываем ответ.
Ответ: 10 попугаев в большой клетке и 5 попугаев в маленькой клетке.
Задание внизу страницы
Ответ:7 ∙ 6 = 42 48 : 6 = 8

15 : 5 = 3 18 : 6 = 3
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3, 4, 5, 6.
Расставляем порядок действий и выполняем вычисления.
7 · 6 = 6 · 7 = 42
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
48 : 6 = 8
так как 6 · 8 = 48
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2 1
16 : (80 − 76) = 4
1) 80 – 76 = 4
2) 16 : 4 = 4
В данном выражении присутствуют действия вычитание и деление, а также скобки. Поэтому вначале выполняем действие в скобках – вычитание, потом вне скобок – деление.
15 : 5 = 3
так как 3 · 5 = 15
где 3 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
18 : 6 = 3
так как 6 · 3 = 18
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
7 ∙ 6 = 42
48 : 6 = 8
16 : (80 − 76) = 16 : 4 = 4
15 : 5 = 3
18 : 6 = 3
Задание на полях страницы
Цепочка:

Ответ:
16 : 4 = 4 4 ∙ 9 = 36 36 : 6 = 6 6 ∙ 5 = 30
1) Выполни действия по порядку.
2) Первая лиловая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
16 : 4 = 4
так как 4 · 4 = 16
где 4 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
4 · 9 = 36
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 6 = 6
так как 6 · 6 = 36
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 5 = 30
где 6 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
16 : 4 = 4
4 ∙ 9 = 36
36 : 6 = 6
6 ∙ 5 = 30
16 : 4 = 4 → 4 · 9 = 36 → 36 : 6 = 6 → 6 · 5 = 30
Номер 8.
Составь равенства, используя выражения.
3 · 4 4 · 6 2 · 6 3 · 2 3 · 8 24 : 4
Ответ:
1) Прежде, чем составить равенства, вычисли значения всех выражений.
2) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6.
Вычисляем значения выражений.
3 · 4 = 12,
где 3 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
4 · 6= 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
2 · 6 = 12,
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
3 · 2 = 6,
где 3 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
24 : 4 = 6,
так как 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Составляем равенства и делаем проверку.
В равенствах правая и левая часть должны быть равны.
3 ∙ 4 = 2 ∙ 6
Проверка:
3 ∙ 4 = 12
2 ∙ 6 = 12
12 = 12
4 ∙ 6 = 3 ∙ 8
Проверка:
4 ∙ 6 = 24
3 ∙ 8 = 24
24 = 24
3 ∙ 2 = 24 : 4
Проверка:
3 ∙ 2 = 6
24 : 4 = 6
6 = 6
Оформляем задание в тетрадь.
12 12
3 · 4 = 2 · 6
24 24
4 · 6 = 3 · 8
6 6
3 · 2 = 24 : 4
Номер 9.
3 · 8 + 3 ◯ 3 · 9
1 см 8 мм ◯ 87 мм
4 · 9 - 9 ◯ 4 · 8
4 дм 5 см ◯ 54 см
3 ∙ 8 + 3 = 3 ∙ 9
27 = 27
7 см 8 мм < 87 мм
78 мм < 87 мм
4 ∙ 9 - 9 < 4 ∙ 8
27 < 32
4 дм 5 см < 54 см
45 см < 54 см
1) Прежде, чем сравнить выражения, вычисли их значения в левой и правой части.
2) Помни о том, что сравнивать численных значения длины можно только, если они выражены в одних единицах измерения.
Рассмотрим выражения и выполним вычисления с пояснениями.
Сравним 3 · 8 + 3 и 3 · 9
Вычислим левую часть 3 · 8 + 3 – это восемь раз по 3 и еще 3, значит, это девять раз по 3. Получается, 3 · 9 = 27, где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Вычислим правую часть 3 · 9 = 27, это девять раз по 3, где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Сравним 27 = 27
Значит, 3 · 8 + 3 = 3 · 9
Ставим знак равно.
Сравним 4 · 9 – 9 и 4 · 8
Вычислим левую часть 4 · 9 – 9 – это четыре раза по 9, но без одного 9, значит, это восемь раз по 4. Получается, 4 · 8 = 32, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Вычислим правую часть 4 · 8 = 32, это по 4 – 8 раз, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Сравним 32 = 32
Значит, 4 · 9 – 4 = 4 · 8
Ставим знак равно.
Сравним 7 см 8 мм и 87 мм
Вычислим левую часть 7 см 8 мм – это 70 мм и еще 8 мм – это 78 мм
Сравним 78 мм < 87 мм
Значит, 7 см 8 мм < 87 мм
Ставим знак меньше.
Сравним 4 дм 5 см и 54 см
Вычислим левую часть 4 дм 5 см – это 40 см да еще 5 см – это 45 см
Сравним 45 см < 54 см
Значит, 4 дм 5 см < 54 см
Ставим знак меньше.
Оформим задание в тетрадь.
3 ∙ 8 + 3 = 3 ∙ 9,
так как 27 = 27
4 ∙ 9 ‒ 9 < 4 ∙ 8,
так как 27 < 32
7 см 8 мм < 87 мм,
так как 78 мм < 87 мм
4 дм 5 см < 54 см,
так как 45 см < 54 см
Номер 10.
7 + 21 : (15 - 8) 60 - (24 + 3) : 3
50 - 24 : (11 - 5) 90 - (28 + 4) : 4
30 + 9 · (14 - 7) 70 - (56 - 7) : 7
10 · 2 : 5
30 : 10 · 7
40 : 10 : 4

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6, 7.
Рассмотрим выражения.
7 + 21 : (15 – 8)
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – сложение.
50 – 24 : (11 – 5)
В выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – вычитание.
30 + 9 · (14 – 7)
В выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, потом умножение и последним действием – сложение.
60 – (24 + 3) : 3
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
90 – (28 + 4) : 4
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
70 – (56 – 7) : 7
В выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – вычитание.
10 · 2 : 5
В выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку справа налево.
30 : 10 · 7
В выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку справа налево.
40 : 10 : 4
В выражении присутствуют действия деления, поэтому выполняем действия по порядку справа налево.
Расставим порядок действий и выполним вычисления.
3 2 1
7 + 21 : (15 − 8) = 10
1) 15 – 8 = 7
2) 21 : 7 = 3
3) 7 + 3 = 10
3 2 1
50 − 24 : (11 − 5) = 46
1) 11 – 5 = 6
2) 24 : 6 = 4
3) 50 − 4 = 46
3 2 1
30 + 9 · (14 − 7) = 93
1) 14 – 7 = 7
2) 9 ∙ 7 = 63
3) 30 + 63 = 93
3 1 2
60 – (24 + 3) : 3 = 51
1) 24 + 3 = 27
2) 27 : 3 = 9
3) 60 − 9 = 51
3 1 2
90 − (28 + 4) : 4 = 82
1) 28 + 4 = 32
2) 32 : 4 = 8
3) 90 − 8 = 82
3 1 2
70 − (56 − 7) : 7 = 63
1) 56 – 7 = 49
2) 49 : 7 = 7
3) 70 − 7 = 63
1 2
10 ∙ 2 : 5 = 4
1) 10 ∙ 2 = 20
2) 20 : 5 = 4
1 2
30 : 10 ∙ 7 = 21
1) 30 : 10 = 3
2) 3 ∙ 7 = 21
1 2
40 : 10 : 4 = 1
1) 40 : 10 = 4
2) 4 : 4 = 1
Оформим задание в тетрадь.
7 + 21 : (15 − 8) = 7 + 21 : 7 = 7 + 3 = 10
50 − 24 : (11 − 5) = 50 – 24 : 6 = 50 – 4 = 46
30 + 9 ∙ (14 − 7) = 30 + 9 · 7 = 30 + 63 = 93
60 − (24 + 3) : 3 = 60 – 27 : 3 = 60 – 9 = 51
90 − (28 + 4) : 4 = 90 – 32 : 4 = 90 – 8 = 82
70 − (56 − 7) : 7 = 70 – 49 : 7 = 70 – 7 = 63
10 ∙ 2 : 5 = 20 : 5 =
30 : 10 ∙ 7 = 3 · 7 = 21
40 : 10 : 4 = 4 : 4 = 1
Номер 11.
Реши уравнения.
х : 5 = 10 28 - х = 28 х - 15 = 0
х : 7 = 6 72 - х = 7 х - 48 = 7
х : 5 = 10
х = 10 ∙ 5
х = 50
50 : 5 = 10
10 = 10
Ответ: х = 50
28 - х = 28
х = 28 - 28
х = 0
28 - 0 = 28
28 = 28
Ответ: х = 0
х - 15 = 0
х = 0 + 15
х = 15
15 - 15 = 0
0 = 0
Ответ: х = 15
х : 7 = 6
х = 6 ∙ 7
х = 42
42 : 7 = 6
6 = 6
Ответ: х = 42
72 - х = 7
х = 72 - 7
х = 65
72 - 65 = 7
7 = 7
Ответ: х = 65
х - 48 = 7
х = 7 + 48
х = 55
55 - 48 = 7
7 = 7
Ответ: х = 55
1) Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия деления и вычитания.
Рассмотрим уравнения.
х : 5 = 10,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
х : 7 = 6,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
28 – х = 28,
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
72 – х = 7,
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
х – 15 = 0,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х – 48 = 7,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
Решим уравнения.
x : 5 = 10
x = 10 ∙ 5
x = 50
x : 7 = 6
x = 6 ∙ 7
x = 42
28 − x = 28
x = 28 − 28
x = 0
72 − x = 7
x = 72 − 7
x = 65
x − 15 = 0
x = 0 + 15
x = 15
x − 48 = 7
x = 7 + 48
x = 55
Сделаем проверку.
x : 5 = 10
Проверка: вместо неизвестного подставим число 50.
50 : 5 = 10, так как 5 · 10 = 50
10 = 10 – верно.
x : 7 = 6
Проверка: вместо неизвестного подставим число 42.
42 : 7 = 6, так как 6 · 7 = 42
6 = 6 – верно.
28 − x = 28
Проверка: вместо неизвестного подставим число 0.
28 – 0 = 28
Если из числа выесть нуль, то число не изменится.
28 = 28 – верно.
72 − x = 7
Проверка: вместо неизвестного подставим число 65.
72 – 65 = 72 – (62 + 3) = (72 – 62) – 3 = 10 – 3 = 7
7 = 7 – верно.
x − 15 = 0
Проверка: вместо неизвестного подставим число 15.
15 – 15 = 0
Из числа вычесть само число, то получиться нуль.
x − 48 = 7
Проверка: вместо неизвестного подставим число 55.
55 – 48 = 55 – (45 + 3) = (55 – 45) – 3 = 10 – 3 = 7
7 = 7 – верно.
Номер 12.
(Устно.) В куске 20 м ткани. на каждый костюм расходуют по 3 м такой ткани. Можно ли из этого куска сшить 6 костюмов? 7 костюмов?
Ответ:1) 3 ∙ 6 = 18 (м) – ткани на 6 костюмов.
2) 3 ∙ 7 = 21 (м) – ткани на 7 костюмов.
Ответ: можно сшить 6 костюмов, а 7 костюмов нет.
Данная задача: вида «расход на 1 костюм, количество костюм, общий расход» характеризуется зависимостями между компонентами:
Расход 1 костюма · количество костюмов = общий расход.
Общий расход : количество костюмов = расход на 1 костюм.
Общий расход : расход на 1 костюм = количество костюмов.
Оформляем условие в виде таблицы.
Общий расход ткани – 20 метров, а расход на 1 костюм – 3 м. Необходимо сшить 6 костюмов. Проверяю, хватит ли ткани на пошив 6 костюмов. Заполним таблицу данными.
-(2023).jpg)
Рассуждаем.
Количество костюмов – 6, а расход на 1 костюм – 3 метра. Чтобы узнать, сколько ткани израсходую на пошив 6 костюмов, нужно сложить количество ткани на каждый костюм.
Но расход ткани на каждый костюм одинаковый, значит, что сложением одинаковых слагаемых можно заменить умножением.
3 · 6 = 18 (м.) - ткани на 6 костюмов.
Продолжаем рассуждение.
Сравниваем количество ткани в куске и расход на 6 костюмов:
18 м < 20 м
Значит, количества ткани в куске хватит на пошив 6 костюмов.
Записываем ответ.
Ответ: ткани хватит на пошив 6 костюмов.
Оформляем условие в виде таблицы.
Общий расход ткани – 20 метров, а расход на 1 костюм – 3 м. Необходимо сшить 7 костюмов. Проверяю, хватит ли ткани на пошив 7 костюмов. Заполним таблицу данными.
-(2023).jpg)
Рассуждаем.
Количество костюмов – 7, а расход на 1 костюм – 3 метра. Чтобы узнать, сколько ткани израсходую на пошив 7 костюмов, нужно сложить количество ткани на каждый костюм.
Но расход ткани на каждый костюм одинаковый, значит, что сложением одинаковых слагаемых можно заменить умножением.
3 · 7 = 21 (м.) - ткани на 7 костюмов.
Продолжаем рассуждение.
Сравниваем количество ткани в куске и расход на 6 костюмов:
21 м > 20 м
Значит, количества ткани в куске не хватит на пошив 7 костюмов.
Записываем ответ.
Ответ: ткани не хватит на пошив 7 костюмов.
Оформляем условие в виде таблицы.
-(2023).jpg)
Запишем решение.
1) 3 ∙ 6 = 18 (м) − ткани на 6 костюмов.
18 < 20
20 м ткани хватит для пошива 6 костюмов.
2) 3 ∙ 7 = 21 (м) − ткани на 7 костюмов.
21 > 20
20 м ткани не хватит для пошива 7 костюмов, не хватает 1 метра ткани.
Записываем ответ.
Ответ: на 6 костюмов ткани хватит, а на 7 костюмов не хватит.
Номер 13.
Масса ящика с яблоками и трёх одинаковых ящиков с виноградом равна 45 кг. Чему равна масса ящика с виноградом, если масса ящика с яблоками равна 15 кг?
Ответ:Всего – 45 кг
Яблоки – 15 кг
Виноград – 3 ящ. по ? кг
1) 45 - 15 = 30 (кг) – ящики с виноградом.
2) 30 : 3 = 10 (кг)
Ответ: 10 кг масса ящика винограда.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в виде краткой записи или таблицы.
Краткая запись:
-(2023).jpg)
Таблица:
-(2023).jpg)
Рассуждаем.
Общая масса ящика с яблоками и трех ящиков с виноградов равна 45 кг. Она складывается из массы ящиков с яблоками и ящиков с виноградом. Соответственно, чтобы узнать, какова масса трех ящиков с виноградом, нужно из общей массы ящиков вычесть массу ящика с яблоками.
45 − 15 = 30 (кг) – масса 3 ящика с виноградом.
Продолжаем рассуждение.
Получается, 3 ящика весят 30 кг. Причем ящики одинаковые. А общая масса трех ящиков складывается из массы каждого из них. Получается, чтобы узнать, сколько весит один ящик, нужно общую массу ящиков разделить на количество ящиков.
30 : 3 = 10 (кг) – масса 1 ящик винограда.
Записываем ответ.
Ответ: масса одного ящика с виноградом 10 кг.
Решение выражением:
(45 – 15) : 3 = 10 (кг)
Номер 14.
Купили 36 цветных карандашей. Из них 12 карандей были в большой коробке, а остальные − в маленьких коробках, по 6 штук в каждой. Сколько было маленьких коробок с карандашами?
Ответ:Всего – 36 шт.
Большая – 12 шт.
Маленькая – ? к. по 6 шт.
1) 36 − 12 = 24 (шт.) – в маленьких коробках.
2) 24 : 6 = 4 (к.)
Ответ: в 4 маленьких коробках.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в виде краткой записи или таблицы.
Краткая запись:
-(2023).jpg)
Таблица:
-(2023).jpg)
Рассуждаем.
Общее количество карандашей складывается из количества карандашей большой и маленькой коробки. Значит, чтобы узнать, сколько карандашей было в маленьких коробках, нужно из общего количества карандашей вычесть количество карандашей большой коробки.
36 − 12 = 24 (кар.) – в маленьких коробках.
Продолжаем рассуждение.
Маленьких карандашей было 24. Их разложили по 6 штук в коробки. Неизвестно количество коробок. Общее количество карандашей складывается из количества карандашей всех маленьких коробок. Значит, чтобы узнать, сколько было коробок, нужно общее количество карандашей разделить на количество карандашей одной коробки.
24 : 6 = 4 (кор.) - было маленькими.
Записываем ответ.
Ответ: 4 маленьких коробки.
Решение выражением:
(36 – 12) : 6 = 4 (кор.)
Номер 15.
Найди периметр квадрата, длина стороны которого 6 см.
Ответ:а = 6 см
Р = ? см
Р = 6 ∙ 4 = 24 см
Ответ: периметр квадрата 24 см.
Периметр – это сумма длин всех сторон.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
-(2023).jpg)
Квадрат – замкнутая ломаная. Длина ломаной равна сумме длин всех отрезков-звеньев, значит, длина квадрата – сумма длин всех его сторон.
Получается, чтобы узнать, каков периметр квадрата, нужно сложить длины всех его сторон.
Но у квадрата все стороны равны. Значит, сложение одинаковых слагаемых можно заменить умножением. поэтому, чтобы вычислить периметр квадрата, нужно длину стороны квадрата умножить на их количество.
Вычисляем периметр.
6 + 6 + 6 + 6 = 6 · 4 = 24 (см) – периметр квадрата
Записываем ответ.
Ответ: периметр квадрата 24 см.
Номер 16.
В цирке выступали обезьянки на двух- и трёхколёсных велосипедах. Сколько было двух- и трёхколёсных велосипедов, если всего было 8 велосипедов и 21 колесо?
Ответ:1) 8 ∙ 2 = 16 (колёс) − если все велосипеды двухколесные.
2) 21 - 16 = 5 (колёс) − лишние, значит они от трехколесных велосипедов.
3) 8 - 5 = 3 (велосипеда) − двухколесные.
Ответ: 3 двухколёсных и 5 трёхколёсных велосипеда.
Чтобы решить задачу, нужно подобрать такую комбинацию велосипедов, чтобы количество велосипедов могло соответствовать количеству колёс.
Рассуждаем.
Предположим, что двухколесных – 1 велосипед, тогда трехколесных – 7 велосипедов.
Проверим:
1) 2 · 1 = 2 (к.) – у одного двухколёсного велосипеда.
2) 3 · 7 = 21 (к.) – у семи трёхколёсных велосипедов.
3) 2 + 21 = 23 (к.) – всего.
23 > 21 – не подходит.
Продолжаем рассуждение.
Предположим, что двухколесных – 2 велосипеда, тогда трехколесных – 6 велосипедов.
Проверим:
1) 2 · 2 = 4 (к.) – у двух двухколёсных велосипедов.
2) 3 · 6 = 18 (к.) – у шести трёхколёсных велосипедов.
3) 4 + 18 = 22 (к.) - всего.
22 > 21 – не подходит.
Продолжаем рассуждение.
Предположим, что двухколесных – 3 велосипеда, тогда трехколесных – 5 велосипедов.
Проверим:
1) 2 · 3 = 6 (к.) – у трёх двухколёсных велосипедов.
2) 3 · 5 = 15 (к.) – у пяти трёхколёсных велосипедов.
3) 6 + 15 = 21 (к.) – всего.
21 = 21 – подходит.
Записываем ответ.
Ответ: 5 – велосипедов трехколесные и 3 – велосипедов двухколесные.
Рассуждаем.
Представим, что все велосипеды двухколёсные. Всего велосипедов 8. Поэтому, чтобы узнать сколько всего колёс нужно количество велосипедов умножить на количество колёс.
8 ∙ 2 = 16 (колес) – у 8 велосипедов, если бы они были все двухколесными.
Продолжаем рассуждение.
Мы знаем, что всего 21 колесо у двухколёсных и трёхколёсных велосипедов. Узнаем сколько колёс останется, если все бы велосипеды были двухколёсными.
21 − 16 = 5 (колес) − осталось неиспользованными.
Значит эти колёса относятся к трехколесным велосипедам.
В итоге трехколесных велосипедов − 5.
Продолжаем рассуждение.
Общее велосипедов складывается из количества двухколесных велосипедов и трехколесных велосипедов. Соответственно, чтобы узнать, сколько всего двухколесных велосипедов, нужно из общего количества велосипедов вычесть количество трехколесных велосипедов.
8 − 5 = 3 (велосипеда) − двухколесных.
Проверяем решение.
5 трехколесных велосипедов и 3 двухколесных.
3 · 5 = 15 (колёс) – у трёхколёсных велосипедов.
2 · 3 = 6 (колёс) – у двух колёсных велосипедов.
15 + 6 = 21 (колесо) – всего.
21 = 21 – верно.
Записываем ответ.
Ответ: 5 – велосипедов трехколесные и 3 – велосипедов двухколесные.
Задание на полях страницы.
Какая фигура лишняя?

1) Лишняя фигура третья сверху – треугольник, так как остальные фигуры состоят из круга и квадрата.
2)Лишняя фигура вторая сверху – круг, потому что внутри других фигур находятся круги, а в этой – квадрат.
1) Чтобы понять, какая фигура лишняя, рассмотри все.
2) Сравним их, из каких элементов они состоят.
Рассмотрим фигуры.
-(2023).jpg)
Сделаем вывод.
Лишними могут быть две фигуры:
1) Лишняя фигура 2, так как так как у неё внутренняя фигура не круг, как в остальных, а квадрат.
-(2023).jpg)
2) Лишняя фигура 3, так как это единственная фигура в которой есть треугольник.
-(2023).jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.