Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 37

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 37

Номер 1.

1) У Васи 2 машинки, а у Коли в 3 раза больше, чем у Васи. Сколько машинок у Коли?
2) У Вити 2 машинки, а у Миши на 3 машинки больше, чем у Вити. Сколько машинок у Миши?
Сравни задачи, а затем реши их.

Ответ:

Задачи отличаются тем, что в первой нужно выполнить действие умножение, потому что сказано «в 3 раза больше», а во второй – сложение, потому что сказано «на 3 больше».
Задача 1: 2 ∙ 3 = 6 (м.) – у Коли. Ответ: 6 машинок было у Коли.
Задача 2: 2 + 3 = 5 (м.) – у Миши. Ответ: 5 машинок у Миши всего.

Подсказка:

1) Задача 1:
«в 3 раза больше», значит, 3 раза по столько, т.е. умножить на 3.

2) Задача 2:
«на 3 больше», значит, вычисляется сложением, т.е прибавить 3.

Задача 1.

Шаг 1.
Рассуждаем.

У Васи было 2 машинки, а у Коли – в 3 раза больше, чем у Васи. В 3 раза больше, значит, 3 раза по столько машинок, сколько их у Коли.

2 · 3 = 6 (м.) – у Коли.

Шаг 2.
Записываем ответ.

Ответ: 6 машинок.

Задача 2.

Шаг 1.
Рассуждаем.

У Вити 2 машинки, а у Миши – на 3 машинки больше, чем у Вити. На 3 машинки больше, значит, что их столько же, сколько у Вити и еще 3 машинки.

2 + 3 = 5 (м.) – у Миши.

Шаг 2.
Записываем ответ.

Ответ: 5 машинок.

Сравним задачи:

В первой задаче одно число в несколько раз больше другого, поэтому она решается с помощью умножения. В 3 раза больше – это знак умножение.

А во второй задаче одно число больше другого на некоторое число и решается сложением. На 3 больше – это знак сложение.

Номер 2.

Ответ:

5 + 3 < 5 ∙ 3 7 + 7 < 7 ∙ 3
6 ∙ 4 = 4 ∙ 6 8 ∙ 2 < 8 ∙ 3
2 + 2 = 2 ∙ 2 9 + 9 = 9 ∙ 2

Подсказка:

1) Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.

2) Сравни записанное в левой и правой частях, чтобы понять, какой знак поставить.

Шаг 1.
Рассмотрим выражения.

Сравним 5 + 3 и 5 · 3.
Вычислим значение левой части: 5 + 3 = 8.
Вычислим значение правой части: 5 · 3 = 5 + 5 + 5 = 15.
Сравним значения: 8 < 15.
Значит, 5 + 3 < 5 · 3.
Ставим знак меньше.

Сравним 7 + 7 и 7 · 3.
Вычислим значение левой части 7 + 7 = 7 · 2 = 14.
Вычислим значение правой части: 7 · 3 = 21.
Сравним значения: 7 > 3.
Значит, 7 + 7 < 7 · 3.
Ставим знак меньше.

Сравним 6 · 4 и 4 · 6.
6 · 4 – это по 6 – 4 раза,
4 · 6 – это по 4 – 6 раз.
Множители поменяли свои места, но вот значение произведения не изменилось, ведь 6 · 4 = 24 и 4 · 6 = 24.
Значит, 6 · 4 = 4 · 6 – переместительный закон умножения.
Ставим знак равно.

Сравним 8 · 2 и 8 · 3.
Вычислим левую часть 8 · 2 = 8 + 8 = 16.
Вычислим правую часть 8 · 3 = 8 + 8 + 8 = 24.
Сравним значения: 2 < 3.
Значит, 8 · 2 > 8 · 3.
Ставим знак больше.

Сравним 2 + 2 и 2 · 2.
Вычислим левую часть 2 + 2 = 2 · 2 = 4.
Вычислим правую часть 2 · 2 = 2 + 2 = 4.
Соответственно, сложение одинаковых слагаемых можно заменить умножением.
Поэтому 2 + 2 = 2 · 2.
Ставим знак равно.

Сравним 9 + 9 и 9 · 2.
Вычислим левую часть 9 + 9 = 9 · 2 = 18.
Вычислим правую часть 9 · 2 = 9 + 9 = 18.
Соответственно, сложение одинаковых слагаемых можно заменить умножением.
Поэтому 9 + 9 = 9 · 2.
Ставим знак равно.

Шаг 2.
Оформляем задание в тетрадь.

5 + 3 < 5 ∙ 3, так как 8 < 15
7 + 7 < 7 ∙ 3, так как 14 < 21

6 ∙ 4 = 4 ∙ 6
Применили переместительное свойство умножения.

8 ∙ 2 < 8 ∙ 3, так как 16 < 24

2 + 2 = 2 ∙ 2, так как 4 = 4
Применили замену одинаковых слагаемых умножением.

9 + 9 = 9 ∙ 2, так как 18 = 18
Применили замену одинаковых слагаемых умножением.

Номер 3.

Запиши числа от 4 до 30, которые делятся без остатка на 3; на 4.

Ответ:

4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,26, 27, 28, 29, 30.
Делятся без остатка на 3: 6, 9, 12, 15, 18, 21, 24, 27, 30 Делятся без остатка на 4:4, 8, 12, 16, 20, 24, 28

Подсказка:

1) Числа, которые без остатка делятся на 3 – это числа, которые образуются в таблице умножения;

2) Числа, которые без остатка делятся на 4 – это числа, которые образуются в таблице умножения 4.

Шаг 1.
Выпишем все числа от 4 до 30.

4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,26, 27, 28, 29, 30.

Шаг 2.
Выпишем числа, которые делятся на 3 без остатка.

Вспомним таблицу умножения на 3.

3 · 1 = 3
3 · 2 = 6
3 · 3 = 9
3 · 4 = 12
3 · 5 = 15
3 · 6 = 18
3 · 7 = 21
3 · 8 = 24
3 · 9 = 27
3 · 10 = 30

Число, которое делится на 3 – это каждое третье число.

Числа, делящиеся на 3 без остатка:
6, 9, 12, 15, 18, 21, 24, 27, 30.

Шаг 3.
Выпишем числа, которые делятся на 4 без остатка.

Вспомним таблиц умножения на 4.

4 · 1 = 4
4 · 2 = 8
4 · 3 = 12
4 · 4 = 16
4 · 5 = 20
4 · 6 = 24
4 · 7 = 28
4 · 8 = 32
4 · 9 = 36
4 · 10 = 40

Число, которое делится на 4 – это каждое четвертое число.
Числа, делящиеся на 4 без остатка:
4, 8, 12, 16, 20, 24, 28.

Номер 4.

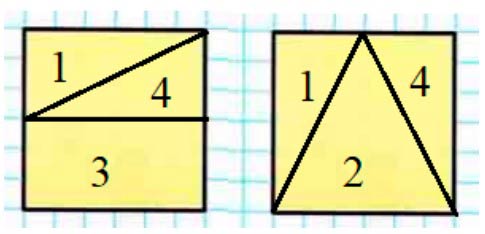
Из каких трех фигур можно составить квадрат? Запиши их номера. У какой из этих фигур есть ось симметрии?

Ответ:

1, 2, 4 или 1, 3, 4. Ось симметрии есть у 2 и 3 фигур.

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 37 номер 4

Подсказка:

1) Квадрат – геометрическая фигура, четырехугольник, у которого все стороны равны.

2) Помни, что фигуры называют по количеству углов.

3) Ось симметрии – линия, которая разбивает фигуру на две равные, при наложении совпадающие.

Шаг 1.
Рассмотрим данные фигуры.

1 – треугольник – три угла.
2 – треугольник – 3 угла.
3 – прямоугольник – 3 угла.
4 – треугольник – 3 угла.

Шаг 2.
Составим из данных фигур квадрат.

Из данных фигур квадрат можно составить двумя способами:
Квадрат 1 – из фигур 1, 3, 4.
Квадрат 2 – из фигур 1, 2, 4.

Шаг 1.
Узнаем у каких фигур есть ось симметрии.

Чтобы узнать есть ли ось симметрии у фигуры, нужно мысленно согнуть фигуру и, если две части совпадут, значит у фигуры есть ось симметрии по сомкнутой линии.

Фигура 1 – треугольник. Все стороны у данного треугольника разные, поэтому оси симметрии у него нет.

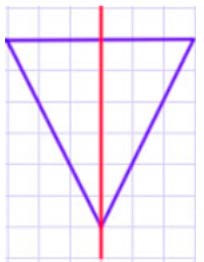
Фигура 2 – треугольник, у которого две боковые стороны равны. У него одна ось симметрии.

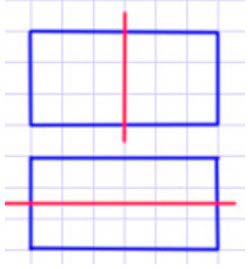
Фигура 3 – прямоугольник. У прямоугольника противоположные стороны равны. У него две оси симметрии – горизонтальная и вертикальная.

Фигура 4 – треугольник. Все стороны у данного треугольника разные, поэтому оси симметрии у него нет.

Значит, ось симметрии есть у фигуры 2 и фигуры 3.

Номер 5.

Ответ:

4 ∙ 8 = 32 24 : 3 = 8 9 ∙ 3 = 27 28 : 7 = 4 6 ∙ 4 = 24 32 : 4 = 8

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 37 номер 5

Подсказка:

1) Помни, что умножение – это замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.

2) Основывайся на переместительном свойство умножения: а · b = b · а.

Шаг 1.
Рассуждаем.

4 · 8 = 32
Вспомни таблиц умножения на 4.

9 · 3 = 3 · 9 = 27
Применим переместительное свойство умножения и таблиц умножения на 3.

6 · 4 = 4 · 6 = 24
Применим переместительное свойство умножения и таблиц умножения на 4.

24 : 3 = 8
Вспомним таблицу умножения на 3. Какое число при умножении на 3 даёт результат 24? Это число 8, так как 3 · 8 = 24.

28 : 7 = 4
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 28? Это число 7, так как 4 · 7 = 28.

32 : 4 = 8
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 32? Это число 8, так как 4 · 8 = 32.

28 – 8 + 37 = (28 – 8) + 37 = 20 + 37 = 57

В данном выражении присутствуют действия сложение и вычитание – они равносильны, поэтому выполняем действия по порядку слева наперво.

45 – 40 + 59 = 5 + 59 = (4 + 1) + 59 = 4 + (59 + 1) = 4 + 60 = 64

В данном выражении присутствуют действия сложение и вычитание – они равносильны, поэтому выполняем действия по порядку слева наперво.

32 – 32 + 18 = (32 – 32) + 18 = 0 + 8 = 8

В данном выражении присутствуют действия сложение и вычитание – они равносильны, поэтому выполняем действия по порядку слева наперво.

44 + 2 ∙ 7 = 44 + 14 = (40 + 10) + (4 + 4) = 58

В данном выражении присутствуют действия сложение и умножение, поэтому первым действием выполняем умножение, а потом сложение.

80 − 8 ∙ 2 = 80 – 16 = (60 + 20) – 16 = 60 + (20 – 16) = 60 + 4 = 64

В данном выражении присутствуют действия вычитание и умножение, поэтому первым действием выполняем умножение, а потом вычитание.

48 − 27 : 3 = 48 – 9 = 48 – (8 + 1) = (48 – 8) – 1 = 40 – 1 = 39

В данном выражении присутствуют действия вычитание и деление, поэтому первым действием выполняем деление, а потом умножение.

Шаг 2.
Оформляем задание в тетрадь.

4 ∙ 8 = 32
9 ∙ 3 = 3 · 9 = 27
6 ∙ 4 = 4 · 6 = 24

24 : 3 = 8
28 : 7 = 4
32 : 4 = 8

1 2
28 − 8 + 37 = 57
1) 28 – 8 = 20
2) 20 + 37 = 57

1 2
45 – 40 + 59 = 64
1) 45 – 40 = 5
2) 5 + 59 = 64

1 2
32 – 32 + 18 = 18
1) 32 – 32 = 0
2) 0 + 18 = 18

2 1
44 + 2 ∙ 7 = 58
1) 2 ∙ 7 = 14
2) 44 + 14 = 58

2 1
80 – 8 ∙ 2 = 64
1) 8 ∙ 2 = 16
2) 80 − 16 = 64

2 1
48 − 27 : 3 = 39
1) 27 : 3 = 9
2) 48 − 9 = 39

Задание внизу страницы

На выставке было 6 рисунков учеников из 4А класса, а рисунков учеников из 4Б в 2 раза больше. Сколько было на выставке рисунков учеников из 4Б класса?

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 37. Задание внизу страницы
6 ∙ 2 = 12 (р.) Ответ: 12 рисунков учеников из 4 Б класса.

Подсказка:

«В 2 раза больше», значит, дважды по столько, т.е вычисляется умножением.

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
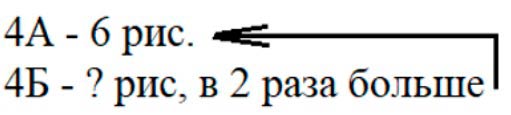
Рассуждаем.

На выставке было 6 рисунков от учеников 4 А, а рисунков учеников из 4 Б – в 2 раза больше. В 2 раза больше, значит, что их столько же, сколько от 4 А, но два раза по столько. Вычисляем умножением.

6 · 2 = 6 + 6 = 12 (рис.) – у 4 Б класса.

Применяем правило замену умножения сложением одинаковых слагаемых.

Шаг 3.
Записываем ответ.

Ответ: 12 рисунков.

Будем учиться читать и строить линейные диаграммы.

На диаграмме (рис. 1) показано, сколько времени каждая из четырёх одноклассниц затрачивает на дорогу от дома до школы.
Сравни диаграммы на рис. 1 и рис. 2. назови их сходство и различие.

На рис. 2 представлена линейная диаграмма. На ней значения величин изображены линиями (отрезками).

Ответ:

Сходство:
Обозначения диаграммы, масштаб
Различие: на рис.1 столбцы, на рис. 2 линии

Подсказка:

Линейная диаграмма отличается от столбчатой только тем, что вместо столбиков чертят отрезки. Чем длиннее отрезок, тем величина больше.

Шаг 1.
Рассмотрим данные диаграммы.

Шаг 2.
Найдем сходства и различия между ними.

Сходство: Обозначения диаграммы, масштаб.

Различие: на рисунке 1 столбцы, на рисунке 2 линии. Соответственно, первая диаграмма – столбчатая, а вторая – линейная.

Номер 1.

Начерти в тетради такую таблицу и перенеси в неё информацию, данную на линейной диаграмме.