Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 26
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Изображение математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 26")
Номер 1.
Рассмотри выражения, установи порядок выполнения действий и выполни вычисления.
Ответ:1)
2)
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитание. Слева направо.
Рассуждаем.
1) 30 + 15 – 6
В данном примере присутствуют только действия сложение и вычитание – они равноправны. Поэтому действия выполняются по порядку слева направо.
60 – 7 + 18
В данном примере присутствуют только действия сложение и вычитание – они равноправны. Поэтому действия выполняются по порядку слева направо.
18 : 3 + 4 · 3
В данном примере присутствуют действия умножение, деление и сложение. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом сложение.
2 · 8 + 21 : 7
В данном примере присутствуют действия умножение, деление и сложение. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом сложение.
12 + 6 : 2 – 7 · 2
В данном примере присутствуют действия умножение, деление, сложение и вычитание. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом сложение и вычитание слева направо.
В данном примере присутствуют действия умножение, деление, сложение и вычитание. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом сложение и вычитание слева направо.
2) 70 : (3 + 7) + 24
В данном примере присутствуют действия сложение и деление, а также скобки. Поэтому вначале выполним действие в скобках – сложение, потом деление и последним действием – сложение.
60 : 6 · 3 – 18
В данном примере присутствуют действия вычитание, умножение и деление. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом действие вычитание.
100 – (24 – 18) · 3
В данном примере присутствуют действия вычитание и умножение, а также скобки. Поэтому вначале выполним действие в скобках – вычитание, потом умножение и последним действием – вычитание.
100 – (72 – 67) · 2
В данном примере присутствуют действия вычитание и умножение, а также скобки. Поэтому вначале выполним действие в скобках – вычитание, потом умножение и последним действием – вычитание.
Расставим действия.
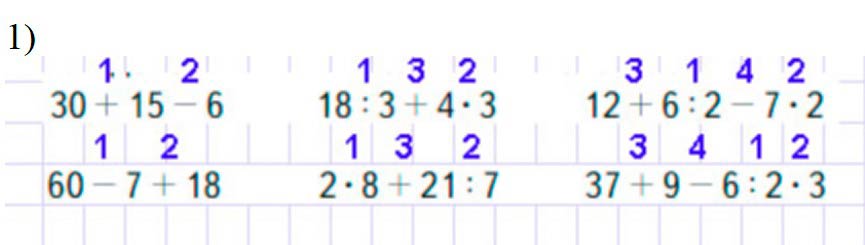
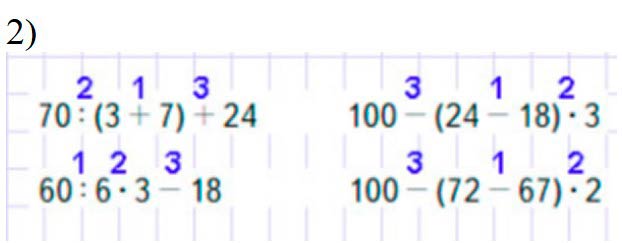
Вычислим по действиям.
1)
30 + 15 – 6 = 39
1) 30 + 15 = 45
2) 45 – 6 = 39
60 – 7 + 18 = 71
1) 60 – 7 = 53
2) 53 + 18 = 71
18 : 3 + 4 ∙ 3 = 18
1) 18 : 3 = 6
2) 4 ∙ 3 = 12
3) 6 + 12 = 18
2 ∙ 8 + 21 : 7 = 19
1) 2 ∙ 8 = 16
2) 21 : 7 = 3
3) 16 + 3 = 19
12 + 6 : 2 – 7 ∙ 2 = 1
1) 6 : 2 = 3
2) 7 ∙ 2 = 14
3) 12 + 3 = 15
4) 15 – 14 = 1
37 + 9 – 6 : 2 ∙ 3 = 37
1) 6 : 2 = 3
2) 3 ∙ 3 = 9
3) 37 + 9 = 46
4) 46 – 9 = 37
2)
70 : (3 + 7) + 24 = 31
1) 3 + 7 = 10
2) 70 : 10 = 7
3) 7 + 24 = 31
60 : 6 ∙ 3 – 18 = 12
1) 60 : 3 = 10
2) 10 ∙ 3 = 30
3) 30 – 18 = 12
100 – (24 – 18) ∙ 3 = 82
1) 24 – 18 = 6
2) 6 ∙ 3 = 18
3) 100 – 18 = 82
100 – (72 – 67) ∙ 2 = 90
1) 72 – 67 = 5
2) 5 ∙ 2 = 10
3) 100 – 10 = 90
Номер 2.
Ответ:
1) Помни, что умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
2) Помни о зависимости между элементами и результатом действия умножения:
1 множитель · 2 множитель = произведение.
Произведение : 1 множитель = 2 множитель.
Произведение : 2 множитель = 1 множитель.
Вычисляем.
8 · 3 = 8 + 8 + 8 = 24
То есть три раза сложили число 8.
21 : 7 = 3
Потому что 7 · 3 = 21
8 : 4 = 2
Потому что 2 · 4 = 8
15 : 5 = 3
Потому что 5 · 3 = 15
6 · 3 = 6 + 6 + 6 = 18
То есть три раза сложили число 6.
18 : 2 = 9
Потому что 9 · 2 = 18
Заполним таблицу.
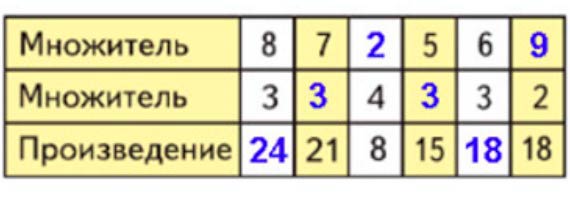
Номер 3.
Упаковщица уложила в коробку 2 ряда желтых кубиков, по 8 кубиков в ряду, и 16 красных кубиков. Сколько всего кубиков было в коробке?
Ответ:
Жёлтые – 2 р. по 8 к.
Красные – 16 к.
Всего – ? к.
1-й способ решения:
1) 2 ∙ 8 = 16 (к.) – желтых.
2) 16 + 16 = 32 (к.)
Ответ: 32 кубика всего в коробке.
2-й способ решения: 2 ∙ 8 + 16 = 16 +16 = 32 (к.) - всего Ответ: 32 кубика.
Помни, что умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие.
Краткая запись:
Жёлтые – 2 ряда по 8 куб.
Красные – 16 к.
Всего – ? к.
Рисунок:
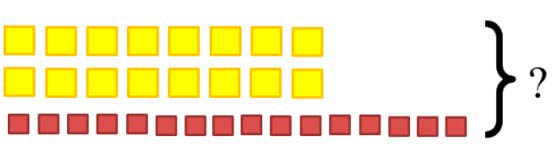
Рассуждаем.
Упаковщица уложила в коробку 2 ряда желтых кубиков – по 8 кубиков в ряду. Значит, общее количество желтых кубиков складывается из количества кубиков первого и второго ряда. Но количество кубиков рядах одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением.
8 · 2 = 16 (куб.)
Продолжаем рассуждения.
Чтобы узнать, сколько кубиков было в коробке всего, нужно сложить количество кубиков красного и желтого цвета.
6 + 16 = 32 (куб.)
Записываем ответ.
Ответ: 32 кубика.
Решение с помощью выражения:
8 · 2 + 16
Номер 4.
В трех одинаковых рядах 24 стула. Сколько стульев в каждом ряду? Сколько стульев в двух таких рядах?
Ответ:3 р. – 24 ст. 1 р. – ? ст. 2 р. – ? ст. 1) 24 : 3 = 8 (ст.) – в одном ряду. 2) 8 + 8 = 16 (ст.) – в двух рядах. Ответ: в одном ряду 8 стульев; в двух рядах 16 стульев.
Данная задача: вида «количество стульев в ряду, количество рядов, общее количество стульев» характеризуется зависимостями между элементами:
Кол-во стульев в 1 ряду · кол-во рядов = общее кол-во.
Общее кол-во : кол-во стульев в 1 ряду = кол-во рядок.
Общее кол-во : кол-во рядок = кол-во стульев в 1 ряду.
Оформляем условие в виде таблицы.
Рассуждаем.
Чтобы узнать, сколько стульев было в 1 ряду, нужно общее количество стульев разделить на количество рядов.
24 : 3 = 8 (ст.) – в одном ряду
Записываем ответ.
Ответ: 8 стульев.
Оформляем условие в виде таблицы.
Теперь мы знаем, что в одном ряду 8 стульев.
Рассуждаем.
Чтобы узнать, сколько стульев в двух рядах, нужно количество стульев сложить. Но ряды одинаковые, значит количество стульев в них равное. Поэтому сложение одинаковых слагаемых можно заменить умножением.
8 · 2 = 16 (ст.) – в двух рядах
Записываем ответ.
Ответ: 16 стульев.
Номер 5.
Высота березы 15 м, а рябины 3 м. На сколько метров береза выше рябины?
Ответ:
15 − 3 = 12 (м)
Ответ: береза выше рябины на 12 м.
Помни, что сравнивать можно только числовые значения длины, выраженные в одних единицах измерения:
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм
1 м = 100 см
Оформляем условие в виде краткой записи или чертежа.
Краткая запись:
Чертёж:
Рассуждаем.
Высота березы – 15 метров, а рябины – 3 метра. Чтобы узнать, на сколько метров высота одного дерева выше другого, нужно из высоты большего дерева вычесть высоту меньшего.
Значит, из высоты березы вычтем высоту рябины:
15 – 3 = 12 (м)
Записываем ответ.
Ответ: на 12 метров береза выше рябины.
Номер 6.
1) Найди периметр каждого многоугольника.
2) Сколько осей симметрии у каждой фигуры?
1) Периметр синего квадрата:
25 + 25 + 25 + 25 = 100 (мм)
100 мм = 10 см
Ответ: периметр ABCD равен 10 см.
Периметр красного треугольника:
3 + 3 + 3 = 3 ∙ 3 = 9 (см)
Ответ: периметр KLM равен 9 см.
Периметр зелёного прямоугольника:
(3 + 3) + (2 + 2) = 6 + 4 = 10 (см)
Ответ: периметр NOPT равен 10 см.
2) В квадрате 4 оси симметрии.
В треугольнике 3 оси симметрии.
В прямоугольнике 2 оси симметрии.
1) Чтобы вычислить периметр вначале нужно с помощью линейки измерить все стороны фигур.
2) Периметр – это сумма длин всех сторон.
3) Ось симметрии – линия, по которой сложив фигуру, две части совпадут, т.е. будут равными и совпадающими.
Рассуждаем.
Многоугольник – замкнутая ломаная.
Из-за того, что многоугольник – замкнутая ломаная, то периметр многоугольника равен длине ломаной. А раз длина ломаной – сумма длин все отрезков-звеньев, то периметр многоугольник – сумма длин всех его сторон.
Измерим стороны многоугольников.
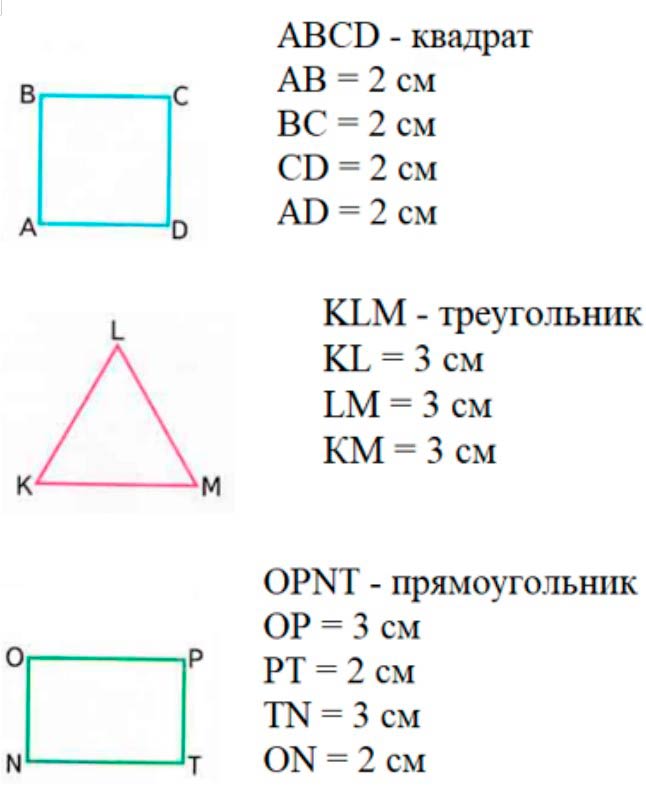
Вычислим периметры АВСD – квадрат.
У квадрата все стороны равны, поэтому сложение одинаковых слагаемых можно заменить умножением:
2 + 2 + 2 + 2 = 2 · 4 = 8 (см) – периметр АВСD
Вычислим периметры KLM – треугольник.
У данного треугольника все стороны равны. Тогда периметр можно вычислить умножением – длину одной стороны умножить на количество сторон:
3 + 3 + 3 = 3 · 3 = 9 (см) – периметр KLM
Вычислим периметры ОРNT – прямоугольник.
Периметр прямоугольник можно вычислить тремя способами:
1) 3 + 2 + 3 + 2 = 10 (см)
Сложив длинны всех сторон.
2) 3 · 2 + 2 · 2 = 6 + 4 = 10 (см)
Так как у прямоугольника противоположные стороны равны, то можно вначале длину и ширину по очереди умножить на 2, а потом полученные произведения сложить.
3) (3 + 2) · 2 = 5 · 2 = 10 (см)
Вначале можно сложить длину и ширину, а потом полученную сумму умножить на 2.
Оси симметрии.
Квадрат имеет 4 оси симметрии: две диагональные оси симметрии, а также горизонтальную и вертикальную оси симметрии.
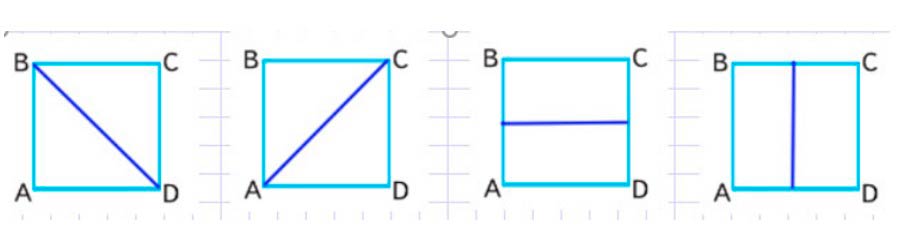
В треугольнике, у которого все стороны равны - 3 оси симметрии:
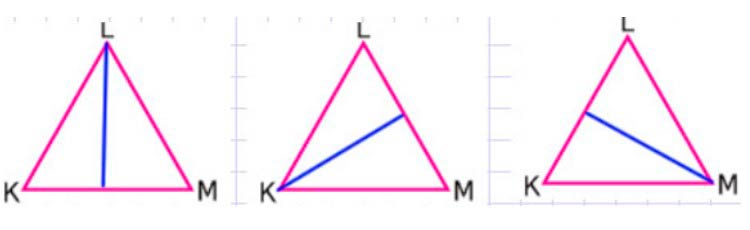
Прямоугольник имеет 2 оси симметрии: горизонтальную и вертикальную оси симметрии.
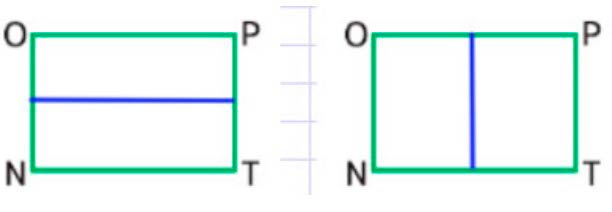
Номер 7.
В двух вазах было 13 яблок. Когда из одной вазы взяли 2 яблока, а в другую добавили 3 яблока, яблок в вазах стало поровну. Сколько яблок было в каждой вазе сначала?
Ответ:1-й способ решения: 1) 13 − 2 + 3 = 14 (ябл.) – стало в двух вазах. 2) 14 : 2 = 7 (ябл.) – стало в одной вазе. 3) 7 + 2 = 9 (ябл.) – было в одной вазе. 4) 7 − 3 = 4 (ябл.) – было во второй вазе. Ответ: в первой вазе было 9 яблок, во второй 4 яблока.
2-й способ решения: 1) (13 – 2 + 3) : 2 + 2 = 14 : 2 + 2 = 7 + 2 = 9 (я.) – было на одной тарелке. 2) (13 – 2 + 3) : 2 – 3 = 14 : 2 – 3 = 7 – 3 = 4 (я.) – было на второй тарелке. Ответ: 9 яблок, 4 яблока.
Эта задача не так проста, как кажется.
1) Сначала подумай, как можно узнать, сколько всего яблок на двух тарелках стало.
2) А затем – сколько яблок на каждой тарелке было, если бы их не докладывали и не убирали.
Узнаем сколько яблок стало.
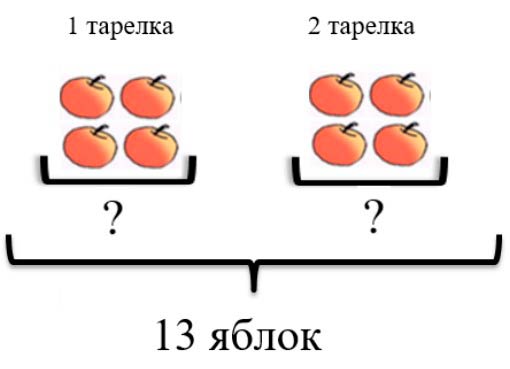
На двух тарелках было 13 яблок. С одной тарелки взяли 2 яблока. Взяли, значит, что их стало меньше. А на другую положили 3 яблока. Положили, значит их стало больше.
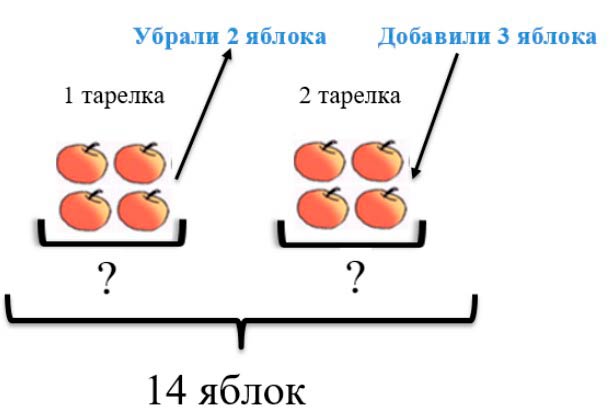
Чтобы узнать, сколько яблок стало на двух тарелках, нужно произвести все действия, что с яблоками производили: вначале вычтем 2 яблока, а потом прибавим 3.
13 – 2 + 3 = 14 яблок стало.
Узнаем сколько яблок стало на каждой тарелке.
текст
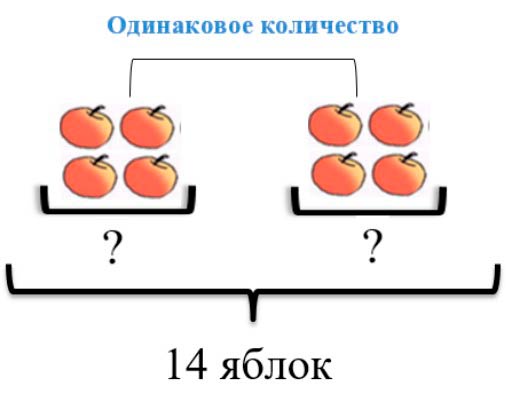
Теперь на двух тарелках 14 яблок и в каждой тарелке одинаковое количество яблок.
Чтобы узнать, сколько яблок стало на каждой тарелке нужно общее количество разделить на два.
14 : 2 = 7 яблок – стало на каждой тарелке.
Узнаем сколько яблок было на каждой тарелке.
Теперь, зная, сколько яблок на одной тарелке, можно узнать, сколько яблок было на каждой тарелке изначально.
Так как из первой тарелки взяли 2 яблока, значит теперь эти 2 яблока нужно добавить:
7 + 2 = 9 (яб.) – было на первой тарелке.
Так как во вторую тарелку положили 3 яблока, значит теперь эти 3 яблока уберём:
7 – 3 = 4 (яб.) – на второй тарелке.
Сделаем проверку.
9 + 4 = 13 (яб.) – было изначально.
Задача решена верно.
Задание внизу страницы
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитанием. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
72 – (47 – 20) : 3
В данном примере присутствуют действия вычитание и деление, а также скобки. Поэтому вначале выполним действие в скобках – вычитание, потом деление и последним действием – вычитание.
21 : (15 – 8 ) ∙ 9
В данном примере присутствуют действия вычитание, умножение и деление, а также скобки. Поэтому вначале выполним действие в скобках – вычитание, а потом умножение и деление по порядку слева направо.
Расставим действия.
3 1 2
72 − (47 − 20) : 3
1 2 3
21 : (15 − 8) ∙ 9
Вычислим по действиям.
72 – (47 – 20) : 3 = 63
1) 47 – 20 = 27
2) 27 : 3 = 9
3) 72 – 9 = 63
21 : (15 – 8 ) ∙ 9 = 27
1) 15 – 8 = 7
2) 21 : 7 = 3
3) 3 ∙ 9 = 27
Задание на полях страницы
Ребусы:
Ответ:
1) Помни, единицы можно складывать и вычитать только с единицами, десятки – с десятками.
2) Помни, что 1 дес. = 10 ед.
Рассмотрим первый ребус.
Первое слагаемое неизвестно целиком. То есть, неизвестно количество единиц и десятков первого слагаемого.
Чтобы найти первое слагаемое, нужно из суммы вычесть второе слагаемое.
83 – 37 = 46 – первое слагаемое.
Запишем решение в столбик:
.jpg)
Рассмотрим второй ребус.
1) Неизвестно количество единиц вычитаемого, но известно количество единиц уменьшаемого и количество единиц разности.
Чтобы найти нужно из количества единиц уменьшаемого вычесть количество единиц разности.
Вспомним какое число при сложении с числом 6 образует в числе 5 единиц. Это число 9, так как 6 + 9 = 15 – это 1 дес. и 5 ед.
9 единиц – у вычитаемого.
2) Неизвестно количество десятков уменьшаемого, но известно количество десятков вычитаемого и количество десятков разности.
Чтобы найти нужно количество десятков разности сложить с количеством десятков вычитаемого.
2 дес. + 3 дес. = 5 дес. и ещё 1 дес., который занимали для вычитания единиц, поэтому 5 дес. + 1 дес. = 6 дес.
6 десятков – у уменьшаемого.
Получаем равенство:
65 – 29 = 36
Запишем решение в столбик:
.jpg)
Страничка для любознательных
Номер 1.
Оля хочет вышить золотой тесьмой на каждом рукаве блузки по 2 таких узора, как на рисунке.
1) Хватит ли для этого 1 м тесьмы? Сколько сантиметров тесьмы потребуется, чтобы закончить вышивку?
2) Можно ли этот узор назвать симметричным? Почему?
3) Хватит ли 100 р. на покупку всей нужной для вышивки тесьмы, если 1 м тесьмы стоит 60 р.?
1) Одного метра не хватит, потребуется ещё 28 см.
Подробно: 1 узор – это 32 см, так как в нём 4 квадрата со стороной 2 см.
Периметр одного квадрата равен 2 ∙ 4 = 8 см.
В одном узоре 4 квадрата, значит 8 ∙ 4 = 32 (см)
На одном рукаве два таких узора.
На один рукав потребуется 32 + 32 = 64 (см) тесьмы.
У Оли два рукава.
На два рукава потребуется 64 + 64 = 128 (см) тесьмы.
2) Этот узор можно назвать симметричным. Потому что можно провести прямую, которая разделит фигуру на равные части.
3) Денег хватит.
Подробно: На 128 см тесьмы потребуется меньше 100 р., потому что 100 см стоят всего 60 р. Остаётся 28 см и 40 р.
Номер 2.
Масса одного щенка и одного котёнка вместе равна 8 кг, а масса трёх таких щенков и двух котят – 22 кг. Найди массу одного котёнка и массу одного щенка.
Ответ:Предположим, что было 3 щенка и 3 котёнка, тогда:
1) 8 · 3 = 24 (кг) - весят 3 щенка и 3 котёнка.
2) 24 - 22 = 2 (кг) - весит котёнок.
3) 8 - 2 = 6 (кг)- весит щенок.
Ответ: масса одного котёнка – 2 кг, масса одного щенка – 6 кг.
Номер 3.
Используя в каждом случае 4 раза цифру 4, знаки арифметических действий и, если надо, скобки, составь 10 выражений со значениями от 1 до 10.
Например:
4 : 4 + 4 - 4 = 1
4 : 4 + 4 : 4 = 2
Если понадобится, то две рядом стоящие цифры можно считать двухзначным числом.
Ответ:(4 ∙ 4 - 4) : 4 = 3
(4 - 4) ∙ 4 + 4 = 4
(4 ∙ 4 + 4) : 4 = 5
(4 + 4) : 4 + 4 = 6
4 ∙ 4 - 4 - 4 = 8
4 ∙ 4 : 4 + 4 = 8
4 - 4 + 4 + 4 = 8
4 : 4 + 4 + 4 = 9
(44 - 4) : 4 = 10
44 : 4 - 4 = 7
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.