Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 25

Шаг 1.
Рассмотрим примеры.

76 – 27 + 9 – 10

В данном примере присутствуют только действия сложение и вычитание – они равноправны. Поэтому действия выполняются по порядку слева направо.

43 – (20 – 7) + 15
В данном примере присутствуют действия сложение и вычитание, а также скобки. Действия в скобках выполняются первыми. Поэтому сначала производится вычитание в скобках, а потом остальные действия по порядку слева направо.

80 : 8 : 2
В данном примере присутствует только действия деления. Поэтому действия выполняются по порядку слева направо.

21 : 7 · 9
В данном примере присутствуют только действия умножение и деление – они равноправны. Поэтому действия выполняются по порядку слева направо: сначала - деление, а потом умножение.

75 – (35 – 30) · 2
В данном примере присутствуют действия умножение и вычитание, а также скобки. Поэтому сначала производится вычитание в скобках, потом умножение и третьим действием выполняем вычитание.

60 : (4 + 6) · 3
В данном примере присутствуют действия умножение, деление и сложение, а также скобки. Поэтому сначала производится сложение в скобках, деление и умножение по порядку справа налево.

Шаг 2.
Расставим действия.

Шаг 3.
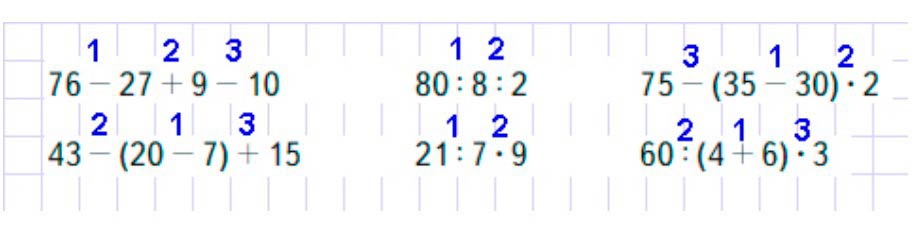
Выполним вычисления по действиям.

76 – 27 + 9 – 10 = 48
1) 76 – 27 = 49

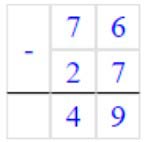
2) 49 + 9 = 58

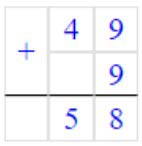
3) 58 – 10 = 48

43 – (20 – 7) + 15 = 45
1) 20 – 7 = 13
2) 43 – 13 = 30
3) 30 + 15 = 45

80 : 8 : 2 = 5
1) 80 : 8 = 10
2) 10 : 2 = 5

21 : 7 ∙ 9 = 27
1) 21 : 7 = 3
2) 3 ∙ 9 = 27

75 – (35 – 30) ∙ 2 = 65
1) 35 – 30 = 5
2) 5 ∙ 2 = 10
3) 75 – 10 = 65

60 : (4 + 6) ∙ 3 = 18
1) 4 + 6 = 10
2) 60 : 10 = 6
3) 6 ∙ 3 = 18

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
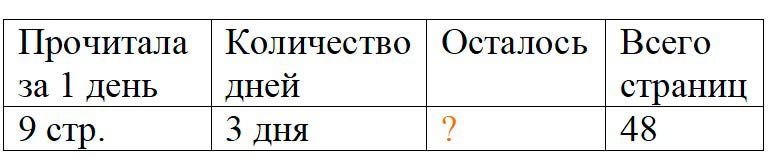
Рассуждаем.

Узнаем сколько страниц прочитано. Даша читала книгу в течение трех дней по 9 страниц ежедневно. Общее количество прочитанных книг складывается из страниц, прочитанного за каждый день.
Чтобы узнать, сколько страниц она прочитала, при этом количество страниц, прочитанного за каждый день, одинаковое. Значит, сложение одинаковых слагаемых можно заменить умножением.

1) 9 · 3 = 27 (стр.)

Шаг 3.
Продолжаем рассуждения.

Узнаем сколько осталось страниц.
Общее количество страниц в книге складывается из количества прочитанных страниц и оставшихся.
Чтобы узнать сколько страниц осталось прочесть, нужно из общего количества страниц в книге вычесть количество прочитанных.

2) 48 – 27 = 21 (стр.)

Шаг 4.
Записываем ответ.

Ответ: 21 страница.

Решение в виде выражения:
48 – (3 · 9)

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Найдём общее количество денег.
Чтобы узнать количество денег детей, нужно сложить деньги брата и сестры.

5 + 7 = 12 (руб.)

Шаг 3.
Продолжаем рассуждения.

Узнаем количество карандашей.
Дети хотят купить карандаши по 3 рубля за карандаш, т.е. цена карандаша одинаковая. Необходимо узнать, сколько таких карандашей можно купить на 12 рублей.
Чтобы это сделать, нужно общую стоимость, т.е. количество денег делим на цену одного карандаша.

12 : 3 = 4 (кар.)

Шаг 4.
Записываем ответ.

Ответ: 4 карандаша.

Решение с помощью выражения:
(5 + 7) : 3

Шаг 1.
Рассуждаем.

Вид данной задачи: на разностное сравнение. Чтобы узнать, на сколько длина одного отрезка больше длины второго отрезка, нужно из длины большего отрезка вычесть длину меньшего.

При этом вычитать можно только числовые значения, выраженные в одних единицах измерения:
1 см = 10 мм
1 дм = 10 см

Шаг 2.
Измерим отрезки.

С помощью линейки измерим отрезки:

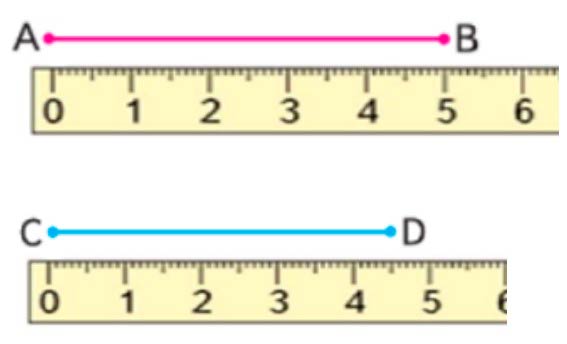
Получаем, что:
Длина отрезка АВ равна 5 см или 50 мм.
Длина отрезка CD равна 4 см 5 мм или 45 мм.

Шаг 3.
Сравним длины отрезков.

Так как отрезок АВ больше отрезка CD, то из длины отрезка АВ вычтем длину отрезка CD:

50 мм – 45 мм = 5 мм

Шаг 4.
Записываем ответ.

Ответ: AB длиннее CD на 5 мм.

Шаг 1.
Рассмотрим уравнения.

х – 18 = 29
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

х + 15 = 25
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

64 – а = 52
а – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

17 + b = 28
b – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

х – 23 = 57
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

48 – х = 20
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Шаг 2.
Выпишем те уравнения, которые решаются сложением и решим их.

х – 18 = 29
х = 29 + 18
х = 47

х – 23 = 57
х = 57 + 23
х = 80

Шаг 3.
Сделаем проверку.

Для проверки решения уравнения, нужно вместо неизвестного подставить получившееся значение. Если правая и левая часть равенства равны, то уравнение решено верно.

х – 18 = 29
Проверка: вместо х подставим число 47.
47 – 18 = 29
29 = 29 – верно

х – 23 = 57
Проверка: вместо х подставим число 80.
80 – 23 = 57
57 = 57 – верно

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
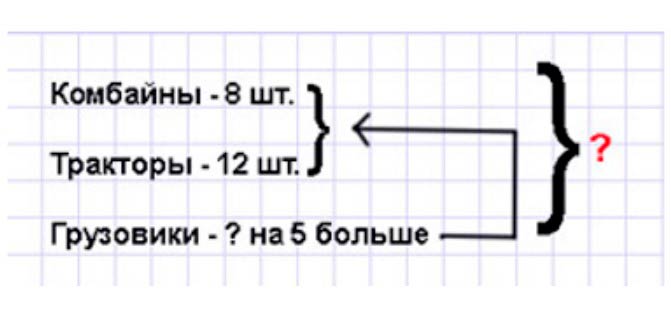
Рассуждаем.

Узнаем сколько комбайнов и тракторов вместе.
В хозяйстве было 8 комбайнов и 12 тракторов.
Чтобы узнать, нужно сложить количество комбайнов и тракторов.

12 + 8 = 20 (шт.) − комбайнов и тракторов вместе

Шаг 3.
Продолжаем рассуждения.

Узнаем сколько грузовиков. Грузовиков на 5 больше, чем комбайнов и тракторов. Значит, что грузовиков в хозяйстве столько, сколько комбайнов и тракторов и еще 5 машин.
Чтобы узнать, нужно к общему количеству тракторов и комбайнов прибавить число 5.

20 + 5 = 25 (шт.) – грузовиков.

Шаг 4.
Продолжаем рассуждения.

Узнаем общее количество машин. Общее количество машин в хозяйстве складывается из количества комбайнов, тракторов и грузовиков. Значит, чтобы узнать, сколько всего машин, нужно сложить количество машин разных видов.

20 + 25 = 45 (шт.) – всего

Шаг 5.
Записываем ответ.

Ответ: 45 машин.

Решение с помощью выражения:
(8 + 12) + (5 + 8 + 12) = 45 (шт.) – техники всего

Шаг 1.
Рассуждаем.

32 + 9 ∙ (19 – 16)

В данном примере присутствуют действия сложение, вычитание и умножение, а также скобки. Поэтому вначале выполним действие в скобках – вычитание, потом умножение и последним действием – сложение.

27 : 3 ∙ 4
В данном примере присутствуют только действия умножение и деление – они равноправны. Поэтому действия выполняются по порядку слева направо.

2 ∙ 9 – 18 : 3
В данном примере присутствуют действия умножение, деление и вычитание. Поэтому вначале выполняем умножение и деление по порядку слева направо, а потом вычитание.

Шаг 2.
Расставим действия.

     3    2      1
32 + 9 ∙ (19 − 16)

    1   2
27 : 3 ∙ 4

  1    3      2
2 ∙ 9 − 18 : 3

Шаг 3.
Вычислим по действиям.

32 + 9 ∙ (19 – 16) = 59
1) 19 – 16 = 3
2) 9 ∙ 3 = 27
3) 32 + 27 = 59

27 : 3 ∙ 4 = 36
1) 27 : 3 = 9
2) 9 ∙ 4 = 36

2 ∙ 9 – 18 : 3 = 12
1) 2 ∙ 9 = 18
2) 18 : 3 = 6
3) 18 – 6 = 12

Шаг 1.
Рассмотрим первый ребус.

1) Количество единиц второго слагаемого неизвестно, но известно количество единиц первого слагаемого и количество единиц суммы.
Чтобы найти нужно из количества единиц суммы вычесть количество единиц второго слагаемого.
Вспомним, при сложении с каким числом число 7 образует 5 единиц. Это число 8, так как 7 + 8 = 15 – это 1 дес. и 5 ед.
8 единиц – во втором слагаемом.

2) Количество десятков первого слагаемого неизвестно, но известно количество десятков второго слагаемого и количество десятков суммы.
Чтоб найти нужно из количества единиц суммы вычесть количество единиц первого слагаемого.
Тогда, 6 дес. – 1 дес. = 5 дес. и ещё 1 дес. занимали для вычисления единиц, поэтому 5 дес. – 1 дес. = 4 дес.
4 десятка – в первом слагаемом.

Шаг 2.
Получаем равенство и записываем решение в столбик.

47 + 18 = 65

Шаг 3.
Рассмотрим второй ребус.

1) Полностью неизвестно уменьшаемое – ни количество единиц, ни количество десятков. Но известно полностью вычитаемое и полностью разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.

60 + 25 = 85 – получили уменьшаемое.

Шаг 4.
Получаем равенство и записываем решение в столбик.

60 + 25 = 85