Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 110

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
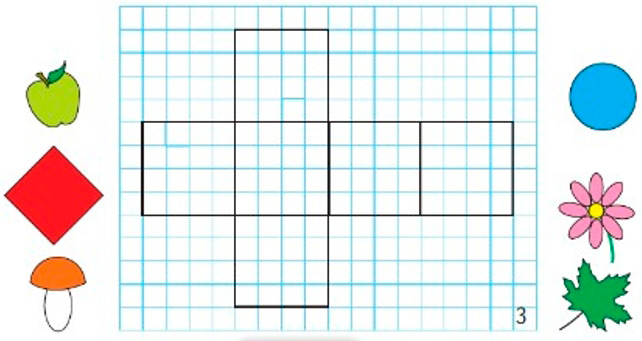
1) Изготовь модель куба по такому плану: перечерти на клетчатую бумагу фигуру (рис. 1). Это развёртка куба. Вырежи её, перегни по красным линиям, намажь клеем «язычки» и склей.
картинка
Поверхность куба состоит из квадратов, их называют гранями куба. Стороны граней называют рёбрами, а вершины граней - вершинами куба (рис. 2).
2) Сосчитай, сколько у куба граней, сколько рёбер, сколько вершин.
3) Хватит ли листа цветной бумаги, площадь которого 1 дм², чтобы обклеить изготовленный куб со всех сторон? Совет. Определи по развёртке, чему равна сумма площадей всех граней куба.

1) Переведя на клетчатую бумагу данную развертку, аккуратно вырезаем ее, не забывая о язычках для склеивания. После этого аккуратно прогибаем ее по всем красным линиям и линиям сгиба язычков для склеивания (можно воспользоваться ножницами ли линейкой и чуть надавливая продавить линии сгибов. Клеем смазать язычки, обозначенные на схеме развертки желтым цветов. В результате мы получив такое объемное тело, как куб, изображенный на рисунке 2 и на полях учебника в верхнем левом углу.
.jpg)
2) Грани – квадраты, из которых и состоит куб. их всего у куба 6.
Ребра – линии, расположенные по бокам всех граней куба. У него их всего 12.
Вершины – это точки, расположенные по углам граней. Их у куба всего 8.
3) Найдем с помощью развертки сумму площадей всех граней куба. Так как куб состоит из 6 граней и все они квадраты, площади поверхности тела можно найти так: 6 ∙ (а ∙ а), где а - сторона квадрата, а а ∙ а – формула для нахождения площади одной грани.
а = 4 клетки или 2 см; площадь всей поверхности = 6 ∙ (2 см ∙ 2 см) = 6 ∙ 4 см = 24 см² – площадь поверхности куба.
Площадь листа бумаги, которым хотят обклеить куб – 1 дм², а 1 дм² = 100 см².
100 см² < 24 см², значит нам хватило бы листа бумаги в 1 дм², чтобы обклеить куб со всех сторон.
Повтори единицы площади.
Изготовим модель куба по плану.
Переведя на клетчатую бумагу данную развертку, аккуратно вырезаем ее, не забывая о язычках для склеивания.
После этого аккуратно прогибаем ее по всем красным линиям и линиям сгиба язычков для склеивания (можно воспользоваться ножницами ли линейкой и чуть надавливая продавить линии сгибов.
Клеем смазать язычки, обозначенные на схеме развертки желтым цветов.
В результате мы получив такое объемное тело, как куб, изображенный на рисунке 2 и на полях учебника в верхнем левом углу.

Сосчитаем грани, ребра и вершины у куба.
Грани – квадраты, из которых и состоит куб. их всего у куба 6.
Ребра – линии, расположенные по бокам всех граней куба. У него их всего 12.
Вершины – это точки, расположенные по углам граней. Их у куба всего 8.
Ответим на вопрос.
Найдем с помощью развертки сумму площадей всех граней куба. Так как куб состоит из 6 граней и все они квадраты, площади поверхности тела можно найти так: 6 ∙ (а ∙ а), где а – сторона квадрата, а а ∙ а – формула для нахождения площади одной грани.
а = 4 клетки или 2 см; площадь всей поверхности = 6 ∙ (2 см ∙ 2 см) = 6 ∙ 4 см = 24 см² – площадь поверхности куба.
Площадь листа бумаги, которым хотят обклеить куб – 1 дм², а 1 дм² = 100 см².
100 см² < 24 см², значит, нам хватило бы листа бумаги в 1 дм², чтобы обклеить куб со всех сторон.
Номер 2.
Начерти в тетради такую же развёртку куба (рис. 3). Нарисуй на ней заданные предметы и геометрические фигуры так, чтобы напротив друг друга были: круг и квадрат; лист и яблоко; гриб и цветок.


Повтори материал о квадрате.
Начертим в тетради развертку куба из учебника.
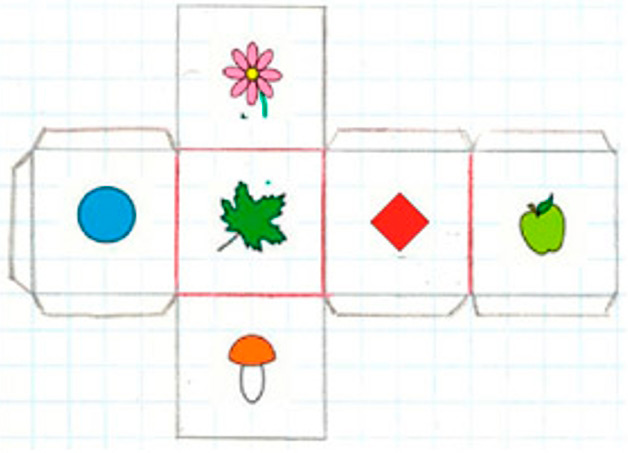
Нарисуем на ней заданные предметы и фигуры.
Диагонали прямоугольника (квадрата) и их свойства
Номер 1.
1) Зная свойства диагоналей прямоугольника, можно построить прямоугольник на нелинованной бумаге, используя только циркуль и линейку.
Начерти любую окружность и проведи в ней 2 любых диаметра. Соедини концы диаметров отрезками.
Проверь, что получился прямоугольник.
2) Начерти в тетради любой прямоугольник, проведи в нём диагонали. Начерти окружность с центром в точке пересечения диагоналей. Объясни, почему окружность проходит через все вершины прямоугольника.

1)
.jpg)
2)
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.