Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 76

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Умножение и деление
Умножение на однозначное число
Задание вверху страницы
Вспомни известные тебе свойства умножения (с. 104, пп. 1,3) и объясни, почему верны равенства:
5 ∙ 17 ∙ 2 = 5 ∙ 2 ∙ 17 (6 + 8) ∙ 4 = 6 ∙ 4 + 8 ∙ 4 (9 + 5 + 1 + 6) ∙ 8 = 9 ∙ 8 + 5 ∙ 8 + 1 ∙ 8 + 6 ∙ 8
Ответ:
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения;
Значение произведения : 1 множитель = 2 множитель;
Значение произведения : 2 множитель = 1 множитель.
Рассмотрим равенства.
5 ∙ 17 ∙ 2 = 5 ∙ 2 ∙ 17 – от перестановки множителей произведение не изменится.
(6 + 8) ∙ 4 = 6 ∙ 4 + 8 ∙ 4 – два соседних множителя можно заменять их произведением.
(9 + 5 + 1 + 6) ∙ 8 = 9 ∙ 8 + 5 ∙ 8 + 1 ∙ 8 + 6 ∙ 8 – при умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Оформим задание в тетрадь.
Номер 325.
Объясни записи в рамках на полях.
Ответ:
с ∙ 1 = с
При умножении любого числа на единицу, произведением будет число, которое умножали.
b ∙ 0 = 0
При умножении любого числа на нуль, произведением будет нуль.
Разные арифметические действия основываются на разных свойствах и правилах, но есть и общие, характерные для всех арифметических действий.
Например, переместительное свойство, сочетательное свойство – они характерны для разных арифметических действий.
А такие свойства, как:
Правило прибавления числа к нулю, 0 + а;
Правило прибавления нуля к числу, а + 0;
Правило умножения числа на 1, а ∙ 1;
Правило умножения числа на 0, а ∙ 0;
Правило деления числа на 1, а : 1;
Правило деления 0 на число, 0 : а.
Рассмотрим записи в рамках на полях.
с ∙ 1 = с
b ∙ 0 = 0
Объясним записи в рамках на полях.
с ∙ 1 = с
При умножении любого числа на единицу, произведением будет число, которое умножали.
b ∙ 0 = 0
При умножении любого числа на нуль, произведением будет нуль.
Номер 326.
Ответ:
А – первый множитель.
b – второй множитель.
а ∙ b – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Чтобы найти произведение, нужно перемножить множители.

а ∙ в – произведение, вычисляется умножением.
Вспомни названия компонентов действия умножения и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения
Значение произведения : 1 множитель = 2 множитель
Значение произведения : 2 множитель = 1 множитель
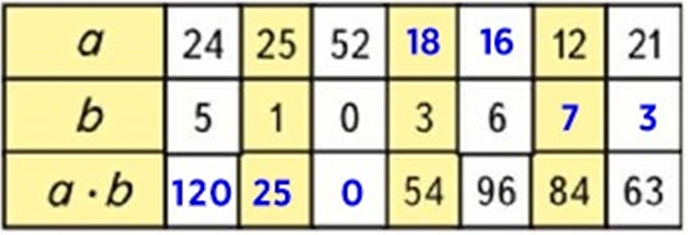
Выполняем вычисления.
24 ∙ 5 = 120, это по 24 – 5 раз, где 24 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых
25 ∙ 1 = 25, потому что если любое число умножить на единицу, то получится число, которое умножали
52 ∙ 0 = 0, потому что если любое число умножить на 0, то получится 0
54 : 3 = 18, потому что 18 ∙ 3 = 54, это по 18 – 3 раза, где 18 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых
96 : 6 = 16, потому что 16 ∙ 6 = 96, это по 16 – 6 раз, где 16 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых
84 : 12 = 7, потому что 12 ∙ 7 = 84, это по 12 – 7 раз, где 12 – одинаковое слагаемое, а 7 количество одинаковых слагаемых
63 : 21 = 3, потому что 3 ∙ 21 = 63, это по 3 – 21 раз, где 3 – одинаковое слагаемое, а 21 – количество одинаковых слагаемых
Оформляем задание в тетрадь.
А – первый множитель.
b – второй множитель.
а ∙ b – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Чтобы найти произведение, нужно перемножить множители.
Номер 327.
Запиши произведение чисел a и b и вычисли его значение при а = 72 и b = 3.
Ответ:a ∙ b, если а = 72 и b = 3, то 72 ∙ 3 = 216
а ∙ в – произведение, вычисляется умножением.
Вспомни названия компонентов действия умножения и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения
Выполняем вычисления.
72 ∙ 3 = 216, это по 72 – 3 раза, где 72 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых
Оформляем задание в тетрадь.
a ∙ b
если а = 72 и b = 3, то 72 ∙ 3 = 216
Номер 328.
Составь разные задачи по выражению 16 ∙ 4.
Ответ:
Задача 1:
Мама купила в магазине 16 тетрадей. Каждая тетрадь стоила 4 рубля. Сколько рублей заплатила мама?
16 ∙ 4 = 64 (руб.)
Ответ: 64 рубля заплатила мама.
Задача 2:
Сколько страниц прочитал Антон за 4 дня, если каждый день он читал по 16 страниц?
16 ∙ 4 = 64 (стр.)
Ответ: 64 страницы прочитал Антон.
Задача 1:
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения;
Значение произведения : 1 множитель = 2 множитель;
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «цена тетради, количество тетрадей, общая стоимость тетрадей» характеризуется зависимостями между компонентами:
Цена тетради ∙ количество тетрадей = общая стоимость тетрадей.
Общая стоимость тетрадей : количество тетрадей = цена тетради.
Общая стоимость тетрадей : цена тетради = количество тетрадей.
Задача 2:
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «кол-во страниц в 1 день, количество дней, общее количество страниц» характеризуется зависимостями между компонентами:
Кол-во страниц в 1 день ∙ количество дней = общее кол-во страниц.
Общее кол-во страниц : количество дней = кол-во страниц в 1 день.
Общее кол-во страниц : кол-во страниц в 1 день = количество дней.
Шаг 1.
Составляем первую задачу.
Сколько страниц прочитал Антон за 4 дня, если каждый день он читал по 16 страниц?
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько стоят все тетради, которые купила мама, нужно количество тетрадей умножить на цену одной тетради.
16 ∙ 4 = 64 (руб.)
Записываем ответ.
Ответ: 64 рубля заплатила мама.
Шаг 1.
Составляем вторую задачу.
Сколько страниц прочитал Антон за 4 дня, если каждый день он читал по 16 страниц?
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько страниц прочитал Антон за 4 дня, нужно количество страниц прочитанных в один день умножить на количество дней.
16 ∙ 4 = 64 (стр.)
Записываем ответ.
Ответ: 64 страницы прочитал Антон.
Номер 329.
На 9 одинаковых парников надо 45 м плёнки. Сколько метров плёнки пойдёт на 3 таких парника? Составь и реши задачи, обратные данной.
Ответ:
1) 45 : 9 = 5 (м) – плёнки для 1-ого парника.
2) 5 ∙ 3 = 15 (м)
Ответ: 15 метров плёнки для 3-х парников.
Обратная задача 1:
На 3 одинаковых парника потратили 15 м плёнки. Сколько метров плёнки надо для 9-ти одинаковых парников?

1) 15 : 3 = 5 (м) – плёнки для 1-ого парника.
2) 5 ∙ 9 = 45 (м)
Ответ: 45 метров плёнки для 9-ти парников.
Обратная задача 2:
Всего для парников было выделено 45 метров плёнки. На 3 парника потратили 15 метров плёнки. Сколько ещё парников можно сделать?

1) 15 : 3 = 5 (м) – плёнки для 1-ого парника. 2) 45 - 15 = 30 (м) - плёнки без трёх парников. 2) 30 : 5 = 6 (шт.) - парников ещё можно сделать. Ответ: 6 парников ещё можно сделать.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «количество плёнки на 1 парник, количество парников, общее количество плёнки» характеризуется зависимостями между компонентами:
Кол-во плёнки на 1 парник ∙ кол-во парников = общее кол-во плёнки.
Общее кол-во плёнки : кол-во парников = кол-во плёнки на 1 парник.
Общее кол-во плёнки : кол-во плёнки на 1 парник = кол-во парников.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько метров плёнки расходуется на каждый парник, общее количество плёнки делим на количество парников.
1) 45 : 9 = 5 (м) – плёнки для 1-ого парника.
Продолжаем рассуждение .
Чтобы узнать, сколько плёнки пойдет на 3 таких парника, нужно умножить количество метров пленки для одного парника умножить на количество парников.
2) 5 ∙ 3 = 15 (м)
Записываем ответ.
Ответ: 15 метров плёнки для 3-х парников.
Решение выражением: 45 : 9 ∙ 3
Шаг 1.
Составляем обратную задачу.
На 3 одинаковых парника потратили 15 м плёнки. Сколько метров плёнки надо для 9-ти одинаковых парников?
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько плёнки расходуется на 1 парник, необходимо общее количество плёнки разделить на количество парников.
1) 15 : 3 = 5 (м) – плёнки для 1-ого парника.
2) 5 ∙ 9 = 45 (м)
Продолжаем рассуждение.
Чтобы узнать, сколько плёнки надо для 9-ти одинаковых парников, нужно количество пленки для одного парника умножить на количество парников.
2) 5 ∙ 9 = 45 (м)
Записываем ответ.
Ответ: 45 метров плёнки для 9-ти парников.
Решение выражением: 15 : 3 ∙ 9
Шаг 1.
Составляем обратную задачу.
Всего для парников было выделено 45 метров плёнки. На 3 парника потратили 15 метров плёнки. Сколько ещё парников можно сделать?
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько плёнки расходуется на 1 парник, нужно общее количество плёнки разделить на количество парников.
1) 45 : 9 = 5 (м) – плёнки для 1-ого парника.
Продолжаем рассуждение.
Чтобы узнать, сколько парников можно сделать из плёнки, нужно общее количество плёнки разделить на количество пленки, затрачиваемой на каждый парник.
2) 15 : 3 = 5 (п.)
Записываем ответ.
Ответ: 5 парников можно сделать из 15 метров плёнки.
Решение выражением: 30 : (15 : 3)
Номер 330.
Туристы в первый день прошли 16 км, что составило восьмую часть их маршрута. Сколько километров им осталось пройти?
Ответ:1-й способ решения:
Прошли – 16 км – 1/8 часть
Всего – ? км
Осталось – ? км
1) 16 ∙ 8 = 128 (км) – весь путь.
2) 128 – 16 = 112 (км)
Ответ: 112 км осталось пройти.
2-й способ решения:
Весь путь разделили на 8 одинаковых частей и если одну восьмую часть прошли (16 км), то осталось пройти:
1) 8 – 1 = 7 (ч) – осталось пройти
2) 16 ∙ 7 = (10 + 6) ∙ 7 = 70 + 42 = 112 (км) – осталось пройти
Ответ: 112 км.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех
Одна вторая – половина целого
Одна третья – третья часть от целого
Одна четвертая – четвертинка или четвертая часть от целого
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде краткой записи.
Прошли – 16 км – 1/8 часть
Всего – ? км
Осталось – ? км
Рассуждаем.
Туристы в первый день прошли 16 км – это восьмая часть их маршрута, значит, нам необходимо найти целое по части. Для этого, нужно одну часть умножить на количество частей.
1) 16 ∙ 8 = 128 (км) – весь путь.
Продолжаем рассуждение.
Чтобы узнать, чему равна длина оставшейся части, нужно из общей длины пути вычесть длину пройденной части.
2) 128 − 16 = 112 (км)
Записываем ответ.
Ответ: 112 км осталось пройти.
Решение выражением: (16 ∙ 8) – 16, где 16 ∙ 8 – длина пути
Номер 331.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном;
2) Нахожу цифру сотен в частном;
3) Нахожу, сколько сотен разделили;
4) Нахожу, сколько сотен осталось разделить;
5) Образую второе неполное делимое;
6) Нахожу, количество десятков в частном;
7) Нахожу, сколько десятков разделили;
8) Нахожу, сколько десятков осталось разделить;
9) Образую третье неполное делимое;
10) Нахожу количество единиц в частном;
11) Нахожу, сколько единиц разделили;
12) Нахожу, сколько единиц осталось разделить;
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
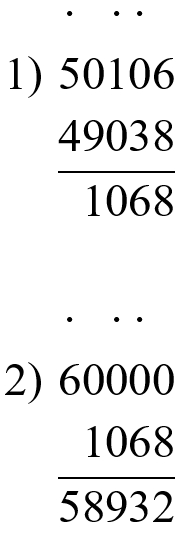
Выполняем вычисления по действиям.
60 000 − (50 106 − 49 038) = 58 932
480 024 − (53 425 + 78 679) = 347 920

Выполняем умножение и деление с устным объяснением.
Пишу: 217 ∙ 4.
Умножаю единицы: 7 ∙ 4 = 28. 28 ед. - это 2 дес. и 8 ед.; 8 ед. пишу под единицами, а 2 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 1 ∙ 4 = 4. К 4 дес. прибавляю 2 дес., которые получены при умножении единиц: 4 + 2 = 6. Пишу 6 под десятками.
Умножаю сотни: 2 ∙ 4 = 8. Пишу 8 под сотнями.
Читаю ответ: 868.
Пишу: 352 ∙ 2.
Умножаю единицы: 2 ∙ 2 = 4. Пишу 4 под единицами.
Умножаю десятки: 5 ∙ 2 = 10. 10 дес. − это 1 сот. и 0 дес., 0 дес. пишу под десятками, а 1 сот. запомню и прибавлю к сотням после умножения сотен.
Умножаю сотни: 3 ∙ 2 = 6. К 6 сот. прибавляю 1 сот., которая получена при умножении десятков: 6 + 1 = 7. Пишу 7 под сотнями.
Читаю ответ: 704.
Пишу: 636 : 6.
Делю сотни: сотен 6.
Разделю 6 на 6. В частном будет 1.
Умножаю: 1 ∙ 6 = 6. Разделили 6 сот.
Вычитаю: 6 − 6 = 0. Сотни разделили все.
Делю десятки: десятков 3, но 3 дес. нельзя разделить на 6 так, чтобы в частном получились десятки. Пишу в частном 0.
Умножаю: 0 ∙ 6 = 0. Разделили 0 дес.
Вычитаю: 3 − 0 = 3. Осталось разделить 3 дес.
Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 6; можно продолжать деление.
Делю единицы: 3 дес. и 6 ед. − это 36 ед.
Разделю 36 на 6. В частном будет 6 ед.
Умножаю: 6 ∙ 6 = 36. Разделили 36 ед.
Вычитаю: 36 − 36 = 0. Единицы разделили все.
Читаю ответ: 106.
Пишу: 736 : 4.
Делю сотни: сотен 7.
Разделю 7 на 4. В частном будет 1.
Умножаю: 1 ∙ 4 = 4. Разделили 4 сот.
Вычитаю: 7 − 4 = 3. Осталось разделить 3 сот.
Сравниваю остаток с делителем: число оставшихся сотен меньше, чем 4; можно продолжать деление.
Делю десятки: 3 сот. и 3 дес. − это 33 дес.
Разделю 33 на 4. В частном будет 8 дес.
Умножаю: 8 ∙ 4 = 32. Разделили 32 дес.
Вычитаю: 33 − 32 = 1. Осталось разделить 1 дес.
Сравниваю остаток с делителем: число оставшихся сотен меньше, чем 4; можно продолжать деление.
Делю единицы: 1 дес. и 6 ед. − это 16 ед.
Разделю 16 на 4. В частном будет 4.
Умножаю: 4 ∙ 4 = 16. Разделили 16 ед.
Вычитаю: 16 − 16 = 0. Единицы разделили все.
Читаю ответ: 184.
Оформляем задание в тетрадь.

Номер 332.
Начерти такой треугольник, дополни его до прямоугольника, найди площадь прямоугольника и каждого треугольника.


S прямоуг. = 3 ∙ 5 = 15 (см2)
15 см2 = 1500 мм2
S треуг. = 1500 : 2 = 750 (мм2)
Ответ: площадь прямоугольника составляет 15 см2, а площади треугольников 750 мм2
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Площадь прямоугольника – произведение длин его сторон. Чтобы вычислить площадь прямоугольника, нужно измерить длины его сторон, а полученные значения перемножить. Вычисляется умножением.
Выполняем чертеж.
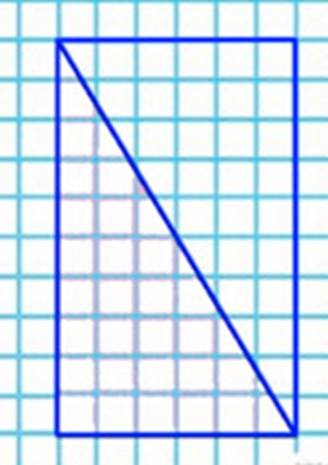
Находим площадь прямоугольника.
S прям. = 3 ∙ 5 = 15 (см2)
15 см2 = 1500 мм2
Находим площадь треугольника.
Чтобы узнать, чему равна площадь одного треугольника, нужно площадь прямоугольника разделить на 2, потому что площади треугольников равны.
S тр. = 1500 : 2 = 750 (мм2)
Задание внизу страницы
Ответ:(14 + 7) ∙ 3 = 63 8 ∙ (100 − 99) = 8
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с
Выполняем вычисления.
(14 + 7) ∙ 3 = 63
1) 14 + 7 = 14 + (6 + 1) = (14 + 6) + 1 = 20 + 1 = 21, по правилу прибавления суммы к числу
2) 21 ∙ 3 = 63, это по 21 – 3 раза, где 21 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых
8 ∙ (100 – 99) = 8
1) 100 – 99 = 100 – (90 + 9) = (100 – 90) – 9 = 10 – 9 = 1, по правилу вычитания суммы из числа
2) 8 ∙ 1 = 8, по правилу умножения числа на единицу
Оформляем задание в тетрадь.
Умножение и деление
Умножение на однозначное число
Вспомни известные тебе свойства умножения (с. 104, пп. 1,3) и объясни, почему верны равенства:
5 ∙ 17 ∙ 2 = 5 ∙ 2 ∙ 17 (6 + 8) ∙ 4 = 6 ∙ 4 + 8 ∙ 4 (9 + 5 + 1 + 6) ∙ 8 = 9 ∙ 8 + 5 ∙ 8 + 1 ∙ 8 + 6 ∙ 8
Ответ:
Номер 329.
Объясни записи в рамках на полях.

с ∙ 1 = с
При умножении любого числа на единицу, произведением будет число, которое умножали.
b ∙ 0 = 0
При умножении любого числа на нуль, произведением будет нуль.
Номер 330.
Ответ:
А – первый множитель.
b – второй множитель.
а ∙ b – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Чтобы найти произведение, нужно перемножить множители.

Номер 331.
Запиши произведение чисел a и b и вычисли его значение при а = 72 и b = 3.
Ответ:a ∙ b, если а = 72 и b = 3, то 72 ∙ 3 = 216
Номер 332.
Составь разные задачи по выражению 16 ∙ 4.
Ответ:
Задача 1:
Мама купила в магазине 16 тетрадей. Каждая тетрадь стоила 4 рубля. Сколько рублей заплатила мама?
16 ∙ 4 = 64 (руб.)
Ответ: 64 рубля заплатила мама.
Задача 2:
Сколько страниц прочитал Антон за 4 дня, если каждый день он читал по 16 страниц?
16 ∙ 4 = 64 (стр.)
Ответ: 64 страницы прочитал Антон.
Номер 333.
На 9 одинаковых парников надо 45 м плёнки. Сколько метров плёнки пойдёт на 3 таких парника? Составь и реши задачи, обратные данной.
Ответ:
1) 45 : 9 = 5 (м) – плёнки для 1-ого парника.
2) 5 ∙ 3 = 15 (м)
Ответ: 15 метров плёнки для 3-х парников.
Обратная задача 1:
На 3 одинаковых парника потратили 15 м плёнки. Сколько метров плёнки надо для 9-ти одинаковых парников?

1) 15 : 3 = 5 (м) – плёнки для 1-ого парника.
2) 5 ∙ 9 = 45 (м)
Ответ: 45 метров плёнки для 9-ти парников.
Обратная задача 2:
Всего для парников было выделено 45 метров плёнки. На 3 парника потратили 15 метров плёнки. Сколько ещё парников можно сделать?

1) 15 : 3 = 5 (м) – плёнки для 1-ого парника. 2) 45 - 15 = 30 (м) - плёнки без трёх парников. 3) 30 : 5 = 6 (шт.) - парников ещё можно сделать. Ответ: 6 парников ещё можно сделать.
Номер 334.
Туристы в первый день прошли 16 км, что составило восьмую часть их маршрута. Сколько километров им осталось пройти?
Ответ:Прошли – 16 км – 1/8 часть
Всего – ? км
Осталось – ? км
1) 16 ∙ 8 = 128 (км) – весь путь.
2) 128 – 16 = 112 (км)
Ответ: 112 км осталось пройти.
Весь путь разделили на 8 одинаковых частей и если одну восьмую часть прошли (16 км), то осталось пройти:
1) 8 – 1 = 7 (ч) – осталось пройти
2) 16 ∙ 7 = (10 + 6) ∙ 7 = 70 + 42 = 112 (км) – осталось пройти
Ответ: 112 км.
Номер 335.
Вычисли.
60000 – (50106 – 49038)
480024 – (53425 + 78679)
101010 + (75372 – 56483)
217 · 4
352 · 2
198 · 7
636 : 6
736 : 4
784 : 8


Номер 336.
Начерти такой треугольник, дополни его до прямоугольника, найди площадь прямоугольника и каждого треугольника.


S прямоуг. = 3 ∙ 5 = 15 (см2)
15 см2 = 1500 мм2
S треуг. = 1500 : 2 = 750 (мм2)
Ответ: площадь прямоугольника составляет 15 см2, а площади треугольников 750 мм2
Задание внизу страницы
Ответ:(14 + 7) ∙ 3 = 63 8 ∙ (100 − 99) = 8
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.