Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 60

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Сложение и вычитание
Номер 260.
(Устно.) Вычисли наиболее лёгким способом.
Ответ:2 + 96 + 98 + 904 = (2 + 98) + (96 + 904) = 100 + 1000 = 1100 257 + 18 + 12 + 3 + 40 = (257 + 3) + (18 + 12) + 40 = 260 + 30 + 40 = (260 + 40) + 30 = 300 + 30 = = 330 48 + 530 + 70 + 52 = (48 + 52) + (530 + 70) = 100 + 600 = 700 33 + 34 + 35 + 36 + 37 =(33 + 37) + (34 + 36) + 35 =70 + 70 + 35 = 140 + 35 = 175
- Объясни, как выполнено сложение и вычитание.

При записи столбиком сложения и вычитания чисел с большим количеством разрядов пользуются правилом: единицы записываются под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч и так далее.
Первый пример:
Записываем разряды под разрядами и приступаем к сложению.
Складываем единицы: шесть плюс два будет восемь.
Складываем десятки: два плюс девять будет одиннадцать. Пишем единицу, а 1 десяток запоминаем.
Складываем сотни: один плюс два будет три, да еще один-четыре.
Складываем единицы тысяч: три плюс четыре получится 7.
Читаем ответ: семь тысяч четыреста восемнадцать.
Второй пример:
Записываем разряды под разрядами. Видим, что данный пример на вычитание. Приступаем к решению.
Вычитаем единицы: от шести семь не отнимешь, значит, занимаем десяток. Шестнадцать минус семь будет девять.
Вычитаем десятки: было четыре стало три, потому что заняли десяток. Три минус ноль будет три.
Вычитаем сотни: от трех четыре не отнимешь, значит, занимаем десяток. Тринадцать минус четыре будет девять.
Вычитаем единицы тысяч: было 5, занимали единицу, осталось 4. От 4 отнять 3 получится 1.
Сносим десятки тысяч в ответ.
Читаем ответ: двадцать одна тысяча девятьсот тридцать девять.
Наиболее легким способом, т.е. рациональными. Помни о том, что относительно арифметического действия сложения существуют некоторые свойства:
Переместительное свойство – от перестановки мест слагаемых значение суммы не изменяется.
Сочетательное свойство – любые два соседних числа можно заменить их суммой.
Выполняем устно вычисления первого столбика.
2 + 96 + 98 + 904 = (2 + 98) + (96 + 904) = 100 + 1000 = 1100
257 + 18 + 12 + 3 + 40 = (257 + 3) + (18 + 12) + 40 = 260 + 30 + 40 = (260 + 40) + 30 = 300 + 30 = = 330
Выполняем устно вычисления второго столбика.
48 + 530 + 70 + 52 = (48 + 52) + (530 + 70) = 100 + 600 = 700
33 + 34 + 35 + 36 + 37 = (33 + 37) + (34 + 36) + 35 = 70 + 70 + 35 = 140 + 35 = 175
Рассмотрим данные записи.
При записи столбиком сложения и вычитания чисел с большим количеством разрядов пользуются правилом: единицы записываются под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч и так далее.

Объясним, как выполнено сложение.
Записываем разряды под разрядами и приступаем к сложению.
Складываем единицы: шесть плюс два будет восемь.
Складываем десятки: два плюс девять будет одиннадцать. Пишем единицу, а 1 десяток запоминаем.
Складываем сотни: один плюс два будет три, да еще один-четыре.
Складываем единицы тысяч: три плюс четыре получится 7.
Читаем ответ: семь тысяч четыреста восемнадцать.
Объясним, как выполнено вычитание.
Записываем разряды под разрядами. Видим, что данный пример на вычитание. Приступаем к решению.
Вычитаем единицы: от шести семь не отнимешь, значит, занимаем десяток. Шестнадцать минус семь будет девять.
Вычитаем десятки: было четыре стало три, потому что заняли десяток. Три минус ноль будет три.
Вычитаем сотни: от трех четыре не отнимешь, значит, занимаем десяток. Тринадцать минус четыре будет девять.
Вычитаем единицы тысяч: было 5, занимали единицу, осталось 4. От 4 отнять 3 получится 1.
Сносим десятки тысяч в ответ.
Читаем ответ: двадцать одна тысяча девятьсот тридцать девять.
Оформляем задание в тетрадь.
Номер 261.
Объясни, что означают записи в рамках на полях.

1) b + 0 = b, если к любому числу прибавить 0, то получится это же число. 2) 0 + c = c, если к нулю прибавить любое число, то получится прибавленное число. 3) a – 0 = a, если из любого числа вычесть 0, то получится это же число. 4) k – k = 0, если из любого числа вычесть себя же, то получится 0.
Помни о том, что в математике существуют частные случаи сложения: прибавления нуля к числу (а + 0), прибавления числа к нулю (0 + а), вычитания из числа единицы (а – 1), прибавления к числу единицы (а + 1), вычитания числа из самого себя (а – а), вычитания нуля из числа (а – 0).
Рассмотрим данные записи.
b + 0 = b
0 + c = c
a – 0 = a
k – k = 0
Объясним, что означает каждая из них.
1) b + 0 = b, если к любому числу прибавить 0, то получится это же число.
2) 0 + c = c, если к нулю прибавить любое число, то получится прибавленное число.
3) a – 0 = a, если из любого числа вычесть 0, то получится это же число.
4) k – k = 0, если из любого числа вычесть себя же, то получится 0.
Номер 262.
Вычисли, записывая решение столбиком, и проверь сложение вычитанием, а вычитание сложением.
Ответ:
Помни о том, что существует алгоритм письменного сложения и вычитания. Многозначные числа необходимо записывать предельно внимательно, чтобы каждый разряд стоял под разрядом. Следуй алгоритму письменного сложения и вычитания:
Сложение:
1) Записываю первое слагаемое так, чтобы каждый знак стоял в отдельной клетке, ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы каждый разряд стоял под своим разрядом;
3) Провожу черту, обозначающую знак равно;
4) Сложение начинаю с единиц низшего разряда. Складываю единицы.
5) Складываю десятки (и так до максимального разряда).
6) Сложение окончено. Читаю ответ. Значение суммы от сложения ...
Вычитание:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда.
5) Вычитаю десятки (и так до максимального разряда).
6) Вычитание окончено. Читаю ответ. Значение разности от вычитания.
Рассуждаем, как будем решать первый столбик.
528 047 + 106 875 (аналогично 385 746 + 23352)
1) Записываю первое слагаемое так, чтобы каждый знак стоял в отдельной клетке, ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы каждый разряд стоял под своим разрядом;
3) Провожу черту, обозначающую знак равно;
4) Сложение начинаю с единиц низшего разряда. Складываю единицы: 7 ед. + 5 ед. = 12 ед. – это 1 дес. 2 ед., значит, 2 единицы записываю, а 1 десяток запоминаю.
5) Складываю десятки: 4 дес. + 7 дес. = 11 дес. да еще 1 дес. – 12 дес. – это 1 сот. 2 дес., значит, 2 десятка записываю, а 1 сот. запоминаю.
6) Складываю сотни: 0 сот. + 8 сот. = 8 сот да еще 1 сот. = 9 сот., 9 сотен меньше, чем 10 сотен, значит, 9 сотен записываю в разряд сотен.
7) Складываю тысячи: 8 тыс. + 6 тыс. = 14 тыс. – это 1 дес. тыс и 4 тыс, значит, 4 тысячи записываю, а 1 десяток тысяч запоминаю;
8) Складываю десятки тысяч: 2 дес. тыс. + 0 дес.тыс. = 2 дес.тыс. да еще 1 дес. тыс. – 3 дес. тыс.
9) Складываю сотни тысяч: 5 сот. тыс. + 1 сот. тыс. = 6 сот. тыс. 6 сотен тысяч меньше, чем 10 сотен тысяч, значит, в разряд сотен тысяч записываю 6 сотен тысяч.
10) Сложение окончено. Читаю ответ. Значение суммы от сложения 528 047 и 106 875 равно 634 922.
Выполняем вычисления с проверкой.
320 260 – 21 476 (аналогично 605 209 – 353 672)
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда; вычитаю единицы: 0 ед. – 6 ед. – вычесть нельзя, значит, занимаю 1 дес., тогда, 10 ед. – 6 ед. = 4 ед. 4 ед. меньше, чем 10 ед., значит, в разряд единиц записываю 4 единицы.
5) Вычитаю десятки: в уменьшаемом 6 десятков да еще 1 десяток занимали. Тогда, в уменьшаемом 5 дес. вычита.: 5 дес. – 7 дес. – вычесть нельзя. Значит, занимаю 1 сотню. Получается, 15 дес. – 7 дес. = 8 дес.
6) Вычитаю сотни: 2 сот. в уменьшаемом да еще 1 сотню занимали. Тогда, 2 сот. – 1 сот. = 1 сот. вычитаю: 1 сот. – 4 сот. – вычесть нельзя. Значит, занимаю одну тысячу. Получается, 11 сот. – 4 сот. = 7 сот.
7) Вычитаю тысячи: в уменьшаемом 0 тыс. да еще 1 тыс. занимали – 9 тыс. тогда, 9 тыс. – 1 тыс. = 8 тыс.
8) Вычитаю десятки тысяч: в уменьшаемом 2 дес.тыс., но 1 дес.тыс. занимали. Получается, что в уменьшаемом 1 дес. тыс. вычитаю: 1 дес.тыс. – 2 дес. тыс – вычесть нельзя. Значит, замани. 1 сот.тыс. Тогда, 11 дес. тыс. – 2 = 9 дес. тыс.
9) В уменьшаемом 3 сот.тыс. да еще 1 сот. тыс занимали – 2 сот.тыс.
10) Вычитание окончено. Читаю ответ. Значение разности от вычитания 21 476 из 320 260 равно 298 784.
Выполняем вычисления с проверкой.

Оформляем задание в тетрадь.
Номер 263.
В соревнования участвовало 18 семей, состоящих из 3 человек, и 16 семей, состоящих из 4 человек. Сколько это всего человек?
Ответ:
1) 3 ∙ 18 = 54 (чел.) – в 18 семьях.
2) 4 ∙ 16 = 64 (чел.) – в 16 семьях.
3) 54 + 64 = 118 (чел.)
3 ∙ 18 + 4 ∙ 16 = 118 (чел.)
Ответ: 118 человек всего участвовало в соревнованиях.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «кол-во человек в 1 семье, количество семей, общее количество человек» характеризуется зависимостями между компонентами:
Кол-во человек в 1 семье · кол-во семей = общее кол-во человек.
Общее кол-во человек: кол-во семей = кол-во человек в 1 семье.
Общее кол-во человек : кол-во человек в 1 семье = кол-во семей.
Оформляем условие в виде краткой записи.

Рассуждаем.
Узнаем, сколько человек в 18 семьях, для этого количество семей умножим на количество человек в них.
1) 3 ∙ 18 = 54 (чел.) – в 18 семьях.
Продолжаем рассуждение.
Узнаем, сколько человек в 16 семьях, для этого количество семей умножим на количество человек в них.
2) 4 ∙ 16 = 64 (чел.) – в 16 семьях.
Продолжаем рассуждение.
Общее количество человек складывается из количества человек обеих групп семей. Значит, чтобы узнать, сколько всего человек участвовало в соревнованиях нужно сложить количество человек семей первой группы и второй.
3) 54 + 64 = 118 (чел.).
Записываем ответ.
Ответ: 118 человек всего.
Решение выражением: 3 ∙ 18 + 4 ∙ 16 = 118 (чел.).
Номер 264.
После того как школьникам было выдано 327 книг, в библиотеке осталось на 246 книг меньше, чем было выдано. Сколько всего книг в библиотеке?
Ответ:
1) 327 − 246 = 81 (кн.) – осталось.
2) 327 + 81 = 408 (кн.)
Ответ: 408 книг было в библиотеке.
Помни о зависимости между частью и целым:
часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.
Оформляем условие в виде краткой записи.

Рассуждаем.
Школьникам было выдано 327 книг, а осталось – на 246 книг меньше. Значит, что осталось книг столько, сколько выдали, но без 246. Получается, чтобы узнать, сколько книг осталось, нужно из количества выданных книг вычесть 246.
1) 327 – 246 = 81 (кн.) – осталось.
Продолжаем рассуждение.
Мы узнали, что осталось книг 81 штука. При этом общее количество книг в библиотеке складывается из количества выданных книг и оставшихся. Значит, чтобы узнать, сколько книг было в библиотеке, нужно сложить количество выданных и оставшихся книг.
2) 327 + 81 = 408 (кн.).
Записываем ответ.
Ответ: 408 книг было в библиотеке.
Решение выражением: 327 + (327 – 246)= 408 (кн.).
Номер 265.
Составь задачу по выражению: 100 − (68 + 14)
Ответ:На склад привезли 100 игрушек, из них 14 кукол и 68 мячей, а остальные игрушки были машинки. Сколько было машинок?
Всего – 100 шт.
Куклы – 14 шт.
Мячи – 68 шт.
Машинки – ? шт.
100 – (68 + 14) = 18 (шт.)
Ответ: 18 машинок всего привезли на склад.
Помни о зависимости между частью и целым:
часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.
Составляем задачу по выражению.
На склад привезли 100 игрушек, из них 14 кукол и 68 мячей, а остальные игрушки были машинки. Сколько было машинок?
Оформляем условие в виде краткой записи.
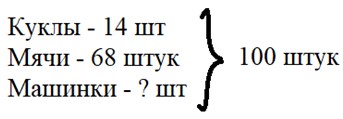
Рассуждаем.
Общее количество кукол и мячей складывается из количества обоих видов игрушек. Значит, чтобы узнать, сколько всего игрушек этого вида было на складе, складываем количество кукол и мячей (68 + 14).
Общее количество игрушек складывается из количества игрушек, которые известны и количество которых неизвестно. Значит, чтобы знать, сколько машинок было на складе, из общего количества игрушек вычитаем общее количество известных.
100 – (68 + 14) = 18 (шт.).
Записываем ответ.
Ответ: 18 машинок.
Номер 266.
(Устно.)
Ответ:999 + 1 = 1000
1000 – 1 = 999
10000 – 1 = 9999
9999 + 1 = 10000
50000 – 1 = 49999
80000 – 1 = 79999
а + 1, значит, увеличить число на единицу, прибавить, вычисляется сложением.
а – 1, значит, уменьшить число на единицу, вычесть, вычисляется вычитанием.
Выполняем устно вычисления первого столбика.
999 + 1 = (990 + 9) + 1 = 990 + (9 + 1) = 990 + 10 = 1000, по правилу прибавления числа к сумме. 1000 – 1 = (990 + 10) – 1 = 990 + (10 – 1) = 990 + 9 = 999, по правилу вычитания числа из суммы.
Выполняем устно вычисления второго столбика.
10 000 – 1 = (9990 + 10) – 1 = 9990 + (10 – 1) = 9990 + 9 = 9999, по правилу вычитания числа из суммы.
9999 + 1 = (9990 + 9) + 1 = 9990 + (9 + 1) = 9990 + 10 = 10 000, по правилу прибавления числа к сумме.
Выполняем устно вычисления третьего столбика.
50 000 – 1 = (49990 + 10) – 1 = 49990 + (10 – 1) = 49990 + 9 = 49999, по правилу вычитания числа из суммы.
80 000 – 1 = (79990 + 10) – 1 = 79990 + (10 – 1) = 79990 + 9 = 79 999, по правилу вычитания числа из суммы.
Задание внизу страницы.
Вычисли.
Ответ:1050 – 50 = 1000 20000 + 800 = 20800 35840 – 840 = 35000
Сумма чисел – слагаемые – знак плюс.
Вспомните, как заменить сумму разрядных слагаемых числом.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Выполняем вычисления.
1050 – 50 = (1000 + 50) – 50 = 1000 + (50 – 50) = 1000, по правилу вычитания числа из суммы.
20 000 + 800 = 20 единиц класса тысяч и 800 единиц класса единиц. Значит, 20 800.
35 840 – 840 = (35 000 + 840) – 840 = 35 000 + (840 – 840) = 35 000, по правилу вычитания числа из суммы.
Оформляем задание в тетрадь.
1050 – 50 = 1000
20000 + 800 = 20800
35840 – 840 = 35000
Задание на полях страницы.
Ребус.

394 − 285 = 109
Помни о названии компонентов действия вычитания и зависимости между компонентами и результатами действия вычитания:
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Рассуждаем и выполняем вычисления.
Данный ребус основан на арифметическом действии вычитания.
Количество единиц уменьшаемого равно 4, а значения разности – 9, но количество единиц вычитаемого - неизвестно.
Чтобы узнать, сколько единиц в вычитаемом, нужно из количества единиц уменьшаемого вычесть количество единиц значения разности:
4 ед. – 9 ед. – вычесть нельзя, значит занимали 1 десяток.
Получается, 14 ед. – 9 ед. = 5 ед.
Выходит, в вычитаемом 5 единиц. Количество десятков уменьшаемого неизвестно. Значит, чтобы узнать количество десятков уменьшаемого, нужно сложить количество десятков значения разности и вычитаемого.
Тогда, 0 дес. + 8 дес. да еще 1 дес. занимали – 9 десятков.
Получается, что в уменьшаемом 9 десятков. Количество сотен вычитаемого неизвестно.
Чтобы узнать, количество единиц вычитаемого, нужно из единиц уменьшаемого вычесть единицы значения разности.
Тогда, 3 сот. – 1 сот. = 2 сот. Получается, что в вычитаемом 2 сотни.
Получаем равенство: 394 – 285 = 109.
Оформляем задание в тетрадь.
394 – 285 = 109
Сложение и вычитание
Номер 264.
(Устно.) Вычисли наиболее лёгким способом.
Ответ:2 + 96 + 98 + 904 = (2 + 98) + (96 + 904) = 100 + 1000 = 1100 257 + 18 + 12 + 3 + 40 = (257 + 3) + (18 + 12) + 40 = 260 + 30 + 40 = (260 + 40) + 30 = 300 + 30 = = 330 48 + 530 + 70 + 52 = (48 + 52) + (530 + 70) = 100 + 600 = 700 33 + 34 + 35 + 36 + 37 =(33 + 37) + (34 + 36) + 35 =70 + 70 + 35 = 140 + 35 = 175
- Объясни, как выполнено сложение и вычитание.

При записи столбиком сложения и вычитания чисел с большим количеством разрядов пользуются правилом: единицы записываются под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч и так далее.
Первый пример:
Записываем разряды под разрядами и приступаем к сложению.
Складываем единицы: шесть плюс два будет восемь.
Складываем десятки: два плюс девять будет одиннадцать. Пишем единицу, а 1 десяток запоминаем.
Складываем сотни: один плюс два будет три, да еще один-четыре.
Складываем единицы тысяч: три плюс четыре получится 7.
Читаем ответ: семь тысяч четыреста восемнадцать.
Второй пример:
Записываем разряды под разрядами. Видим, что данный пример на вычитание. Приступаем к решению.
Вычитаем единицы: от шести семь не отнимешь, значит, занимаем десяток. Шестнадцать минус семь будет девять.
Вычитаем десятки: было четыре стало три, потому что заняли десяток. Три минус ноль будет три.
Вычитаем сотни: от трех четыре не отнимешь, значит, занимаем десяток. Тринадцать минус четыре будет девять.
Вычитаем единицы тысяч: было 5, занимали единицу, осталось 4. От 4 отнять 3 получится 1.
Сносим десятки тысяч в ответ.
Читаем ответ: двадцать одна тысяча девятьсот тридцать девять.
Номер 265.
Объясни, что означают записи в рамках на полях.

1) b + 0 = b, если к любому числу прибавить 0, то получится это же число. 2) 0 + c = c, если к нулю прибавить любое число, то получится прибавленное число. 3) a – 0 = a, если из любого числа вычесть 0, то получится это же число. 4) k – k = 0, если из любого числа вычесть себя же, то получится 0.
Номер 266.
Вычисли, записывая решение столбиком, и проверь сложение вычитанием, а вычитание сложением.
528047 + 106875
385746 + 23352
680708 + 21926
320260 – 21476
605209 – 353672
304506 – 91358


Номер 267.
В соревнования участвовало 18 семей, состоящих из 3 человек, и 16 семей, состоящих из 4 человек. Сколько это всего человек?
Ответ:
1) 3 ∙ 18 = 54 (чел.) – в 18 семьях.
2) 4 ∙ 16 = 64 (чел.) – в 16 семьях.
3) 54 + 64 = 118 (чел.)
3 ∙ 18 + 4 ∙ 16 = 118 (чел.)
Ответ: 118 человек всего участвовало в соревнованиях.
Номер 268.
После того как школьникам было выдано 327 книг, в библиотеке осталось на 246 книг меньше, чем было выдано. Сколько всего книг в библиотеке?
Ответ:
1) 327 − 246 = 81 (кн.) – осталось.
2) 327 + 81 = 408 (кн.)
Ответ: 408 книг было в библиотеке.
Номер 269.
Составь задачу по выражению: 100 – (68 + 14)
Ответ:На склад привезли 100 игрушек, из них 14 кукол и 68 мячей, а остальные игрушки были машинки. Сколько было машинок?
Всего – 100 шт.
Куклы – 14 шт.
Мячи – 68 шт.
Машинки – ? шт.
100 – (68 + 14) = 18 (шт.)
Ответ: 18 машинок всего привезли на склад.
Номер 270.
(Устно.)
999 + 1
1000 – 1
4000 – 1
10 000 – 1
9999 + 1
99 999 + 1
50 000 – 1
80 000 – 1
900 000 – 1
999 + 1 = 1000
1000 − 1 = 999
4000 – 1 = 3999
10000 − 1 = 9999
9999 + 1 = 10000
99 999 + 1 = 100 000
50000 − 1 = 49999
80000 − 1 = 79999
900 000 – 1 = 899 999
Задание внизу страницы.
Вычисли.
Ответ:1050 − 50 = 1000 20000 + 800 = 20800 35840 − 840 = 35000
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.