Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 55

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 22.
Прочитай текст и запиши цифрами числа. В тысяча девятьсот пятьдесят третьем году в Антарктике был обнаружен айсберг длиной сто сорок пять тысяч метров, шириной сорок тысяч метров.
Ответ:1953, 145000 м, 40000 м.
Помни о том, что одна и та же цифра, стоя на разных позициях в записи числа может обозначать количество единиц разных разрядов.
Помни о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайся к таблице, чтобы вспомнить классово-разрядный состав числа.

Следуй плану, для того, чтобы записать многозначное число:
1) Записываю сколько единиц в числе высшего разряда.
2) Записываю количество единиц следующего разряда.
3) Прочитываю число по плану на с.24 для самопроверки:
1. разбей число на классы, отсчитывая справа по 3 цифры.
2. читай, сколько в числе единиц каждого класса, начиная с высшего, не произнося название классе единиц.
Внесем числа из текста в таблицу.
Помни, что цифра указывает на количество единиц того или иного разряда:
Тысяча девятьсот пятьдесят третий год.

Значит, 1 единица класса тысяч и 953 единицы класса единиц: 1953.
Сто сорок пять тысяч метров.

Значит, 145 единиц класса тысяч и 0 единиц класса единиц: 145 000.
Сорок тысяч метров.

Значит, 40 единиц класса тысяч и 0 единиц класса единиц: 40 000.
Оформим задание в тетрадь.
1953, 145000 м, 40000 м.
Номер 23.
Высота надводной части айсберга 30 м, это восьмая часть всей его высоты. На какую глубину айсберг уходит под воду?
Ответ:1-й способ решения:
1) 30 ∙ 8 = 240 (м) – высота всего айсберга.
2) 240 – 30 = 210 (м)
2-й способ решения:

Всего 8 частей.
Над водой одна часть.
8 – 1 = 7 (ч) – под водой.
30 ∙ 7 = 3 дес. ∙ 7 = 21 дес. = 210 (м)
Ответ: 210 м глубина айсберга в воде.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Вид задачи: на нахождение целого по части.
Оформляем условие в виде схематического чертежа.

Можно дополнить рассуждения рисунком.
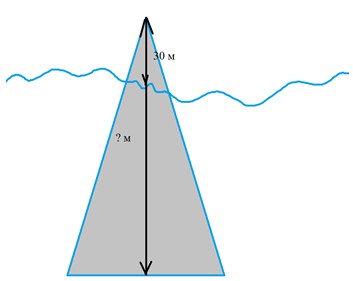
Рассмотрим 1 способ решения.
Высота надводной части – 30 м – это одна восьмая часть всей его высоты. Значит, чтобы узнать, чему равна общая высота айсберга, умножим высоту надземной части на 8.
30 · 8 = 240 (м) – высота айсберга.
Высота айсберга складывается из высоты надводной и подводной части. Значит, чтобы узнать, какова высота подводной части, нужно из высоты айсберга вычесть высоту надводной части.
240 – 30 = 210 (м) – высота подводной части.
Рассмотрим 2 способ решения.
У айсберга две части: надводная и подводная. Значит, 7 частей приходится на подводную часть. И на каждую часть приходится 30 м.
Значит, чтобы узнать, сколько метров приходится на подводную часть – 7 частей, умножаем размер одной части на их количество.
30 м. · 7 = 210 м.
Оформляем задание в тетрадь.
1-й способ решения:
1) 30 ∙ 8 = 240 (м) – высота всего айсберга.
2) 240 − 30 = 210 (м).
Ответ: 210 м глубина айсберга в воде.
2-й способ решения:
8 – 1 = 7 (ч) – под водой.
30 ∙ 7 = 210 (м).
Ответ: 210 м глубина айсберга в воде.
Номер 24.
Школьники пошли на экскурсию в Музей космонавтики в 11 ч. Дорога до музея и обратно заняла 1 ч, осмотр музея – 1 ч 10 мин. Когда школьники возвратились с экскурсии?
Ответ:Начало – 11 ч.
Дорога – 1 ч.
В музее – 1 ч 10 мин.
Окончание – ? ч.
1) 1 ч + 1 ч 10 мин = 2 ч 10 мин – время, потраченное на дорогу и осмотр музея.
2) 11 ч + 2 ч 10 мин = 13 ч 10 мин.
Ответ: 13 ч 10 мин время возвращения.
Вспомни, как расположены цифры, обозначающие часы на циферблате. Используя их, ответь на вопросы.
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек.
1 час – 60 мин.
1 сут = 24 часа.
Оформляем условие в виде краткой записи.
Начало – 11 ч.
Дорога – 1 ч.
В музее – 1 ч 10 мин.
Окончание – ? ч.
Рассуждаем.
Вся экскурсия состоит из нескольких частей: дорога до и из музея, время в музее. Для того, чтобы узнать, когда школьники возвратились с экскурсии, сначала узнаем, сколько времени они потратили на саму экскурсию.
Общее время экскурсии складывается из времени в пути и музее. Значит, чтобы узнать, сколько времени потратили школьники, складываем время, проведенное в музее и дороге.
1) 1 ч + 1 ч 10 мин = 2 ч 10 мин – время, потраченное на дорогу и осмотр музея.
Продолжаем рассуждение.
Мы узнали, что на экскурсию они потратили 2 ч 10 мин. Значит, чтобы узнать, в какое время вернулись школьники, нужно к времени начала прибавить длительность экскурсии.
2) 11 ч + 2 ч 10 мин = 13 ч 10 мин.
Записываем ответ.
Ответ: 13 ч 10 мин время возвращения.
Номер 25.
Бегемот может съесть за день 60 кг трав, а слон — 300 кг. Сколько тонн травы требуется бегемоту и слону на 10 дней? Реши задачу разными способами.
Ответ:
1-й способ решения:
1) 60 + 300 = 360 (кг) — съедают бегемот и слон за день.
2) 360 ∙ 10 = 3600 (кг)
3600 кг = 3 т 600 кг
2-й способ решения:
1) 60 ∙ 10 = 600 (кг) — травы нужно бегемоту на 10 дней.
2) 300 ∙ 10 = 3000 (кг) — травы нужно слону на 10 дней.
3) 600 + 3000 = 3600 (кг)
3600 кг = 3 т 600 кг
Ответ: 3 т 600 кг требуется бегемоту и слону на 10 дней.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «масса корма в 1 день, количество дней, общее количество корма» характеризуется зависимостями между компонентами:
Кол-во корма в день · кол-во дней = общее кол-во корма.
Общее кол-во корма : кол-во дней = кол-во корма в 1 день.
Общее кол-во корма : кол-во корма в 1 день = кол-во дней.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество корма складывается из количества корма, расходуемого в каждый из дней.
1) 60 + 300 = 360 (кг) – съедают бегемот и слон за день.
Продолжаем рассуждение.
Значит, чтобы узнать сколько корма было израсходовано за 10 дней, складываем количество корма, расходуемого каждый день. Но количество корма, расходуемого в один день одинаковое. Поэтому, сложение одинаковых слагаемых заменяем умножением. Тогда, количество корма в 1 день умножаем на количество дней.
2) 360 ∙ 10 = 3600 (кг).
3600 кг = 3т 600 кг.
Записываем ответ.
Ответ: 3т 600кг требуется бегемоту и слону на 10 дней.
Решение выражением:
(60 + 300) · 10, где 300 + 60 – расход корма в день на двух животных.
Шаг 1.
Рассуждаем.
Узнаем, сколько травы нужно бегемоту на 10 дней. Для этого, количество корма за 1 день умножаем на 10.
1) 60 ∙ 10 = 600 (кг) – травы нужно бегемоту на 10 дней.
Продолжаем рассуждение.
Узнаем, сколько травы нужно слону на 10 дней. Для этого, количество корма за 1 день умножаем на 10.
2) 300 ∙ 10 = 3000 (кг) – травы нужно слону на 10 дней.
Продолжаем рассуждение.
Узнаем, сколько травы нужно слону и бегемоту на 10 дней, для этого сложим полученные ранее значения.
3) 600 + 3000 = 3600 (кг).
3600 кг = 3т 600кг.
Записываем ответ.
Ответ: 3т 600кг требуется бегемоту и слону на 10 дней.
Решение выражением:
60 · 10 + 300 · 10, где 60 · 10 – количество корма, съедаемое за 10 дней бегемотом, а 300 · 10 – количество корма, съедаемого за 10 дней слоном.
Номер 26.
Два велосипедиста выехали из двух пунктов навстречу друг другу. Когда первый проехал 1 км 180 м, второй проехал 820 м. На какое расстояние сблизились велосипедисты?
Ответ:
Первый велосипедист - 1 км 180 м
Второй велосипедист - ? 820 м
Всего - ? м
1 км 180 м = 1180 м
1180 м + 820 м = 2000 м
2000 м = 2 км
Ответ: на 2 км сблизились велосипедисты.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 10 дм.
1 м = 100 см.
1 км = 1000 м.
Помни о зависимости между частью и целым:
часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.
Оформляем условие в виде схематического чертежа.
Два велосипедиста выехали из двух пунктов навстречу друг другу. То есть, выполним схематический чертеж, где отразим направление движения велосипедистов.
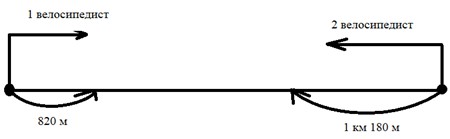
Рассуждаем.
Между ними было некоторое расстояние Х. В какой-то определенный момент велосипедисты начали движение друг навстречу другу. Одинаковое время они ехали так, что первый велосипедист проехал 820 метров, а второй – 1 км 180 м. Условно они остановились и именно в этот момент нам нужно определить, на сколько они сблизились.
Чтобы это понять еще раз посмотрим на схематический чертеж:
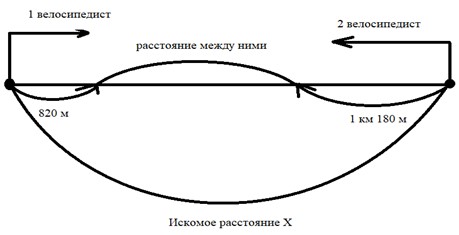
Продолжаем рассуждение.
Искомое расстояние Х складывается из расстояния, которое они преодолели, и которое между ними есть. Значит, то расстояние, что они прошли вместе и есть расстояние, на которое они сблизились. Значит, чтобы узнать, на какое расстояние они сблизились, складываю расстояние, пройденное каждым велосипедистом.
1 км 180 м = 1180 м.
1180 м + 820 м = 2000 м.
2000 м = 2 км.
Записываем ответ.
Ответ: на 2 км сблизились велосипедисты.
Номер 27.
Спиши, заполняя пропуски.
Ответ:700 дм2 = 7 м2.
30 см2 = 3000 мм2.
8 дм2 = 800 см2.
1437 см2 = 14 дм2 37 см2.
2415 мм2 = 24 см2 15 мм2.
46030 дм2 = 460 м2 30 дм2.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Рассуждаем и заполняем пропуски.
700 дм2; 1 м2 – это 100 дм2, потому что 10 дм · 10 дм = 100 дм2, значит, 700 дм2 : 100 дм2 = 7 м2.
30 см2; 1 см2 – это 100 мм2, потому что 10 мм · 10 мм = 100 мм2, значит, 100 мм2 · 30 = 3 000 мм2.
8 дм2; 1 дм2 – 100 см2, потому что 10 см · 10 см = 100 см2, значит, 100 см2 · 8 = 800 см2.
1437 см2; 1 дм2 – это 100 см2, потому что 10 см · 10 см = 100 см2, значит, 1437 см2 : 100 см2 = 14 (ост. 37), значит, 14 дм2 37 см2.
2415 см2; 1 см2 – это 100 мм2, потому что 10 мм · 10 мм = 100 мм2, значит, 2415 см2 : 100 мм2 = 24 (ост. 15), значит, 24 см2 15 мм2.
46 030 дм2, 1 м2 – это 100 дм2, потому что 10 дм · 10 дм = 100 дм2, значит. 46 030 дм2 : 100 дм2 = 460 (ост.) 30, значит, 460 м2 30 дм2.
Оформляем задание в тетрадь.
700 дм2 = 7 м2.
30 см2 = 3000 мм2.
8 дм2 = 800 см2.
1437 см2 = 14 дм2 37 см2.
2415 мм2 = 24 см2 15 мм2.
46030 дм2 = 460 м2 30 дм2
Номер 28.
Подбери числа так, чтобы ты мог найти значения выражений, и выполни действия.
Ответ:570 – (40 + 30) = 500
200 + 120 − 320 = 0
1000 – (100 − 50) ∙ 2 = 900
1000 – (1 + 5) : 6 = 999
490 – (45 − 5) = 450
540 – 2 ∙ 20 = 500
Рассмотри каждую запись. На каком действии они основаны. Чтобы понять, в каких границах можно выбирать числа, пойми, при каких числах вы сможете вычислить значение выражения.
Рассуждаем какие числа можно подобрать.
570 − ( + )
Последним действием в данном выражении будет вычитание, потому что сначала выполняются действия в скобках. Так как последним действием будет вычитание, то вычитать нужно такое число, которое будет меньше или равно 570. Значит, нужно подобрать такие числа, сумма которых равна или меньше 570.
+ – 320
Последним действием в данном выражении будет вычитание, потому что скобки в записи отсутствуют, а значит выполняться действия будут справа налево. Значит, сумма первых двух чисел должна быть больше или равна 320.
1000 – ( – ) ·
Первым действием по правилу будет действие в скобках, потому что они влияют на порядок выполнения действий. Выполнив первое действие, переходим ко второму- умножение, а затем вычитание. Соответственно, значение разности и второй множитель должны получиться такими, чтобы их произведение было меньше или равно 1000.
1000 – ( – ) :
Первым действием по правилу будет действие в скобках, потому что они влияют на порядок выполнения действий. Выполнив первое действие, переходим ко второму- деление, а затем вычитание. Соответственно, значение разности и делитель должны получиться такими, чтобы значение частного от их деления было меньше или равно 1000.
490 – ( – )
В данном выражении есть скобки. Они влияют на порядок выполнения действий. Значит, сначала выполняется вычитание в скобках, а потом вычитание вне скобок. Получается, значение разности от вычитания числа в скобках должно быть меньше или равно 490.
540 – ·
В данном выражении нет скобок. Но сначала по правилу выполняется действие умножения, а потом вычитание. Значит, значение произведения от умножения чисел должно быть меньше или равно 540.
Выполняем вычисления, вставляя подобранные числа.
570 – (40 + 30) = 500
200 + 120 – 320 = 0
1000 – (100 – 50) ∙ 2 = 900
1000 – (1 + 5) : 6 = 999
490 – (45 – 5) = 450
540 – 2 ∙ 20 = 500
Оформляем задание в тетрадь.
Вопросы для повторения.
Номер 1.
Какие единицы используют для измерения длины? площади? времени? массы? Назови их, начиная с самой маленькой единицы, которую ты знаешь, и заканчивая самой большой.
Ответ:Для измерения длины: мм, см, дм, м, км. Для измерения площади: мм2, см2, дм2, м2, км2. Для измерения времени: с, мин, ч, сут., нед, мес., год, столетие. Для измерения массы: г, кг, ц, т.
Вспомни определения понятий длина, площадь, время, масса. Назови единицы измерения начиная от самой маленькой до самой большой, т.е. по возрастанию.
Дадим определение длине.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
Дадим определение площади.
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Дадим определение времени.
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек.
1 час – 60 мин.
1 сут – 24 час.
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес.
1 год – 356 сут.
Дадим определение массе.
Масса – величина, которая характеризует вес предмета, то, сколько он весит. Масса может измеряться в таких единицах измерения, как грамм, килограмм, центнер, тонна.
Помни о соотношении числовых значений единиц измерения времени:
1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.
Номер 2.
Зачем нужны различные единицы для измерения одной величины?
Ответ:Это нужно для удобства представления данных и вычислений.
Рассуждай, основываясь на величине масса. Почему используются гири разной массы, разные весы, для чего составляются специальные таблицы мер и весов.
Вспомни, что при изучении темы масса тебе встречалась задача: «Можешь ли ты поднять груз массой 1 000 000 г?». Если бы не существовало величин кроме граммов, смог бы ты ее решить и ответить на вопрос?
Рассуждаем.
Вернемся к задаче из прошлой темы. «Можешь ли ты поднять груз массой 1 000 000 г?». Мы решали ее через перевод маленьких единиц измерения массы в более крупные, а именно:
1) Сначала в килограммы, ведь 1 кг – 1000 г, значит, 1 000 000 : 1 000 = 1 000 кг.
2) Затем в тонны, ведь 1 т. – 1000 кг, значит, 1 000 кг – это 1 тонна.
Если бы мы не сделали этого, то никогда бы не узнали, что груз массой 1 000 000 г не удалось бы поднять ребенку, а тем более взрослому, ведь 1 тонну весит легковой автомобиль.
Продолжаем рассуждение.
А значит, система мер и весов, различные единицы измерения нужны для понимания веса предметов, для грамотной с ними работы, для удобства вычислений.
Очень хороший пример ты можешь вспомнить, если подумаешь, как твоя мама или бабушка или, может быть, ты сам готовишь что-нибудь на кухне, например, печешь пирожки. Для того, чтобы завести тесто, необходимо точно измерить количество дрожжей, сахара, муки и других ингредиентов. А если бы не существовало таких единиц измерения, как грамм, то никогда бы вкусные булочки ни у кого на светы бы и не получились.
Продолжаем рассуждение.
А как важны единицы измерения врачам и фармацевтам, ведь лекарства – это настоящие маленькие лаборатории, где важна точность и единицы измерения очень специфичны. Например, количество некоторых препаратов измеряется в миллиграммах. Эта единица измерения очень важна для того, чтобы создать лекарства, а например, для расчета урожайности она не пригодится.
Вывод.
Различные единицы для измерения одной величины нужны для удобства представления данных и вычислений.
Номер 3.
Как можно найти периметр и площадь прямоугольника?
Ответ:Р = 2 ∙ (a + b), S = a ∙ b, где a и b – стороны прямоугольника.
Ломаная линия – геометрическая фигура, состоящая из отрезков-звеньев. Значит, чтобы вычислить длину ломаной, нужно измерить длины отрезков-звеньев, а полученные значения сложить.
Прямоугольник – замкнутая ломаная.
Площадь фигуры – часть плоскости, занятая фигурой. Площадь может измеряться в единицах измерения: мм2, см2, дм2, м2, км2 и др.
Как найти периметр прямоугольника.
Периметр фигуры – сумма длин всех ее сторон. Чтобы вычислить периметр прямоугольника, нужно измерить длины всех сторон, а полученные значения сложить.
Сделать это можно тремя способами, ведь у прямоугольника противоположные стороны равны:
1 способ:
а + в + а + в
2 способ:
а · 2 + в · 2
3 способ:
(а + в) · 2
Как найти площадь прямоугольника.
Площадь прямоугольника – произведение длин его сторон. Вычисляется по формуле: а · в, где а и в – стороны прямоугольника.
Задание на полях страницы.
△? ☐? ◯?
30 + ☐ = △ △ – 18 = 50 ☐ + ◯ = △
Ответ:30 + 38 = 68 68 – 18 = 50 38 + 30 = 68
Начни решение задачи с того равенства, где вычислить число, прячущееся за фигурой проще. Это равенство 2. Начни с него.
Рассуждаем и выполняем вычисления.
△ – 18 = 50
Треугольник в данном выражении является уменьшаемым. Чтобы найти неизвестное, нужно к значению разности прибавить вычитаемое.
△ = 50 + 18= 68
30 + ☐ = △
Теперь подставим полученное значение в первое равенство. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
☐= 68 – 30= 38
☐ + ◯ = △
Теперь, полученные значения подставляем в третье равенство.
Круг – неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
◯ = 68 – 18 = 50.
Оформляем задание в тетрадь.
30 + 38 = 68
68 – 18 = 50
38 + 30 = 68
Номер 22.
Прочитай текст и запиши цифрами числа. В тысяча девятьсот пятьдесят третьем году в Антарктике был обнаружен айсберг длиной сто сорок пять тысяч метров, шириной сорок тысяч метров.
Ответ:1953, 145000 м, 40000 м.
Номер 23.
Высота надводной части айсберга 30 м, это восьмая часть всей его высоты. На какую глубину айсберг уходит под воду?
Ответ:1-й способ решения:
1) 30 ∙ 8 = 240 (м) – высота всего айсберга.
2) 240 − 30 = 210 (м)
2-й способ решения:

Всего 8 частей.
Над водой одна часть.
8 – 1 = 7 (ч) – под водой.
30 ∙ 7 = 210 (м)
Ответ: 210 м глубина айсберга в воде.
Номер 24.
Школьники пошли на экскурсию в Музей космонавтики в 11 ч. Дорога до музея и обратно заняла 1 ч, осмотр музея – 1 ч 10 мин. Когда школьники возвратились с экскурсии?
Ответ:Начало – 11 ч
Дорога – 1 ч
В музее – 1 ч 10 мин
Окончание – ? ч
1) 1 ч + 1 ч 10 мин = 2 ч 10 мин – время, потраченное на дорогу и осмотр музея.
2) 11 ч + 2 ч 10 мин = 13 ч 10 мин
Ответ: 13 ч 10 мин время возвращения.
Номер 25.
Бегемот может съесть за день 60 кг трав, а слон – 300 кг. Сколько тонн травы требуется бегемоту и слону на 10 дней?
Сколькими способами можно решить эту задачу?
Задачу можно решить двумя способами.

1-й способ решения:
1) 60 + 300 = 360 (кг) — требуется бегемоту и слону на 1 день.
2) 360 ∙ 10 = 3600 (кг) — требуется бегемоту и слону на 10 дней.
3600 кг = 3 т 600 кг.
2-й способ решения:
1) 60 ∙ 10 = 600 (кг) — травы нужно бегемоту на 10 дней.
2) 300 ∙ 10 = 3000 (кг) — травы нужно слону на 10 дней.
3) 600 + 3000 = 3600 (кг) — требуется бегемоту и слону на 10 дней.
3600 кг = 3 т 600 кг.
Ответ: 3 т 600 кг требуется бегемоту и слону на 10 дней.
Номер 26.
Два велосипедиста выехали из двух пунктов навстречу друг другу. Когда первый проехал 1 км 180 м, второй проехал 820 м. На какое расстояние сблизились велосипедисты?
Ответ:
Первый велосипедист - 1 км 180 м
Второй велосипедист - ? 820 м
Всего - ? м
1 км 180 м = 1180 м
1180 м + 820 м = 2000 м
2000 м = 2 км
Ответ: на 2 км сблизились велосипедисты.
Номер 27.
Спиши, заполняя пропуски.
Ответ:700 дм2 = 7 м2.
30 см2 = 3000 мм2.
8 дм2 = 800 см2.
1437 см2 = 14 дм2 37 см2.
2415 мм2 = 24 см2 15 мм2.
46030 дм2 = 460 м2 30 дм2.
Номер 28.
Подбери числа так, чтобы ты мог найти значения выражений, и выполни действия.
Ответ:570 − (40 + 30) = 500
200 + 120 − 320 = 0
1000 − (100 − 50) ∙ 2 = 900
1000 − (1 + 5) : 6 = 999
490 − (45 − 5) = 450
540 − 2 ∙ 20 = 500
Вопросы для повторения.
Номер 1.
Какие единицы используют для измерения длины? площади? времени? массы? Назови их, начиная с самой маленькой единицы, которую ты знаешь, и заканчивая самой большой.
Ответ:Для измерения длины: мм, см, дм, м, км. Для измерения площади: мм2, см2, дм2, м2, км2. Для измерения времени: с, мин, ч, сут., нед, мес., год, столетие. Для измерения массы: г, кг, ц, т.
Номер 2.
Зачем нужны различные единицы для измерения одной величины?
Ответ:Это нужно для удобства представления данных и вычислений.
Номер 3.
Как можно найти периметр и площадь прямоугольника?
Ответ:Р = 2 ∙ (a + b), S = a ∙ b, где a и b – стороны прямоугольника.
Задание на полях страницы
△? ☐? ◯?
30 + ☐ = △ △ – 18 = 50 ☐ + ◯ = △
Ответ:30 + 38 = 68 68 – 18 = 50 38 + 30 = 68
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.