Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 5

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 4.
Ответ:999 + 1 = 1000 900 − 1 = 899

Задание на нахождение значения выражений.
Помним, что 10 единиц низшего разряда образует 1 единицу высшего, т.е:
10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот = 1 тыс.
Вычисление значений выражения сводится к применению правил:
Правило прибавления числа к сумме:
(а + в) + с = (а + с) + в.
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы:
(а + в) – с = (а – с) + в.
Вычислим.
Выполним на черновую следующие удобные вычисления:
999 + 1 = (990 + 9) + 1 = 990 + (9 + 1) = 990 + 10 = 1000, по правилу прибавления числа к сумме
900 – 1 = (890 + 10) – 1 = 890 + (10 – 1) = 890 + 9 = 899, по правилу вычитания числа из суммы
700 + 80 + 9 = 700 + 80 = 780 + 9 = 789
347 – 7 – 40 = 347 – 7 = 340 – 40 = 300
570 + 30 – 330 = 600 – 330 = 600 – (300 + 30) = (600 – 300) – 30 = 270, по правилу вычитания суммы из числа
950 + 50 – 660 = 1000 – 660 = 1000 – (600 + 60) = (1000 – 600) – 60 = 340, по правилу вычитания суммы из числа
Оформляем задание в тетрадь.
999 + 1 = 1000
900 – 1 = 899
700 + 80 + 9 = 789
347 – 7 – 40 = 300
570 + 30 – 330 = 270
950 + 50 – 660 = 340
Номер 5.
(Устно.) В классе 19 человек, из них 9 мальчиков. Сколько в классе девочек? Составь и реши задачи, обратные данной.
Ответ:
19 − 9 = 10 (д.) – в классе
Ответ: 10 девочек в классе.
Обратная задача 1:
В классе 19 человек, из них 10 девочек. Сколько в этом классе мальчиков?
19 − 10 = 9 (м.) – в классе
Ответ: 9 мальчиков в классе.
Обратная задача 2:
В классе 10 девочек и 9 мальчиков. Сколько всего учеников в классе?
10 + 9 = 19 (уч.) – в классе
Ответ: 19 учеников в классе.
Помним о зависимости между частью и целым:
часть + часть = целое
целое – 1 часть = 2 часть
целое – 2 часть = 1 часть
• Условия будем записывать в виде краткой записи.
• Данная задача является на нахождение части по целому.
• Чтобы составить обратную задачу необходимо известное сделать неизвестным, а неизвестное известным.
• Две обрытые задачи будут на нахождение части по целому и на нахождение целого по части.
Шаг 1.
Рассуждаем.
Всего человек в классе – это количество девочек и мальчиков вместе.
Следовательно, чтобы узнать, сколько девочек, нужно из общего количества детей вычесть количество мальчиков. Выполняем действие вычитание.
Запишем числа в таблицу.
19 − 9 = 10 (д.)
Ответ: 10 девочек в классе.
Шаг 1.
Составляем условие обратной задачи.
В классе 19 человек, из них 10 девочек. Сколько в этом классе мальчиков?
Записываем выражение и ответ.
Всего человек в классе – это количество девочек и мальчиков вместе.
Следовательно, чтобы узнать, сколько мальчиков, нужно из общего количества детей вычесть количество девочек. Выполняем действие вычитание.
Записываем выражение и ответ.
19 − 10 = 9 (м.)
Ответ: 9 мальчиков в классе.
Шаг 1.
Составляем условие обратной задачи.
В классе 10 девочек и 9 мальчиков. Сколько всего учеников в классе?
Записываем выражение и ответ.
Общее количество детей складывается из количества мальчиков и девочек. Следовательно, чтобы узнать, сколько всего детей, нужно сложить количество мальчиков и девочек. Выполняем действие сложение.
Записываем выражение и ответ.
10 + 9 = 19 (уч.)
Ответ: 19 учеников в классе.
Номер 6.
Мише 10 лет. Его дедушка в 6 раз старше Миши, а бабушка на 4 года моложе дедушки. Сколько лет Мишиной бабушке? Составь похожую задачу о своих родных.
Ответ:
1) 10 ∙ 6 = 60 (л.) – дедушке.
2) 60 − 4 = 56 (л.) – бабушке.
Ответ: 56 лет бабушке.
Своя задача:

1) 10 ∙ 3 = 30 (л.) – папе.
2) 30 − 1 = 29 (л.) – маме.
Ответ: 29 лет маме.
«в 6 раз старше» – находим значение умножением.
«на 4 года моложе» – находим значение вычитанием.
Свою задачу составляем по примеру данной.
Шаг 1.
Записываем краткую запись.

Рассуждаем.
Если Мише 10 лет, а дедушка в 6 раз больше. Значит, чтобы узнать, сколько лет дедушке, нужно возраст Миши умножить на 6. Выполняем умножение.
10 · 6 = 60 (л.) – дедушке.
Рассуждаем.
Бабушка на 4 года моложе дедушки. Моложе – значит бабушке меньше, чем дедушке на 4 года. Следовательно, чтобы узнать, сколько лет бабушке, нужно из возраста дедушки вычесть 4 года. Выполняем вычитание.
60 – 4 = 56 (л.) – бабушке.
Записываем ответ.
Ответ: 56 лет бабушке.
Решение в виде выражения:
(10 · 6) – 4 = 56.
Шаг 1.
Составляем собственную задачу и записываем её краткую запись.

Рассуждаем.
Если Оле 10 лет, а папа в 3 раза старше Оли. Значит, чтобы узнать, сколько лет папе, нужно возраст Оли умножить на 3. Выполняем умножение.
10 · 3 = 30 (л.) – папе.
Рассуждаем.
Если мама на 1 год младше папы. Младше – это меньше на 1год. Следовательно, чтобы узнать возраст мамы, нужно из возраста папы вычесть 1 год. Выполняем вычитание.
30 – 1 = 29 (л.) – маме.
Записываем ответ.
Ответ: 29 лет маме.
Решение в виде выражения:
(10 · 3) – 1 = 29 (л.).
Номер 7.
Ответ:
290 + 70 = 360
680 + 50 = 730
140 ∙ 6 = 840
260 ∙ 3 = 780
480 : 6 = 80
360 : 9 = 40
Задание на нахождение значения выражений
Помним, что 10 единиц низшего разряда образует 1 единицу высшего, т.е:
10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот = 1 тыс.
Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с
Вычисляем.
980 – 80 – 100 = 900 – 100 = 9 сот. – 1сот. = 8 сот. = 800
640 – 40 + 200 = 600 + 200 = 6 сот. + 2 сот. = 8 сот = 800
290 + 70 = 290 + (10 + 60) = (290 + 10) + 60 = 300 + 60 = 360, по правилу прибавления суммы к числу
680 + 50 = 680 + (20 + 30) = (680 + 20) + 30 = 700 + 30 = 730, по правилу прибавления суммы к числу
140 · 6 = 14 дес. · 6 = 84 дес. = 840
260 · 3 = 26 дес. · 3 = 78 дес. = 780
480 : 6 = 48 дес. : 6 = 8 дес. = 80
360 : 9 = 36 дес. : 9 = 4 дес. = 40
Оформляем задание в тетрадь
Номер 8.

В книге 180 страниц. В первый день ученик прочитал 52 страницы, во второй – 28 страниц. Сколько страниц ему осталось прочитать? Реши задачу двумя способами.
Ответ:
Всего – 180 стр.
Прочитал – 52 стр. и 28 стр.
Осталось – ? стр.
1-й способ решения:
1) 52 + 28 = 80 (стр.) – прочитал всего.
2) 180 − 80 = 100 (стр.) – осталось всего
Ответ: 100 страниц осталось прочитать.
2-й способ решения:
1) 180 − 52 = 128 (стр.) – осталось прочитать после первого дня.
2) 128 − 28 = 100 (стр.) – осталось всего
Ответ: 100 страниц осталось прочитать.
Задача на нахождение остатка
Условие задачи в виде краткой записи
Решение задачи сводится к выражению, основанном на правиле вычитания суммы из числа:
а – (в + с) = (а – в) – с
Записываем краткую запись.
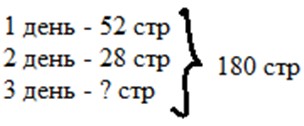
Рассуждаем.
Общее количество прочитанных страниц складывается из количества прочитанных страниц в каждый из дней. Нам известно, сколько было прочитано в 1и во 2 день. Следовательно, мы можем узнать общее количество страниц за 1 и 2 день. Выполняем сложение.
52 + 28 = 80 (стр.) – за 1 и 2 день.
Рассуждаем
Общее количество страниц – это всего за 3 дня. Мы знаем, сколько всего за 1 и 2 день. Следовательно, можем найти, сколько в 3 день было прочитано страниц. Нужно из общего количества страниц вычесть количество прочитанных страниц.
180 – 80 = 100 (стр.) – за 3 день
Записываем ответ.
Ответ: 100 страниц осталось прочитать.
Решение в виде выражения:
180 – (52 + 28) = 100 (стр.).
Рассмотрим другие способы решения.
У данного выражения есть 3 способа решения, они и станут 3 способами решения задачи.
Способ 1:
см. выше 1 решение
Способ 2:
180 – (52 + 28) = (180 – 52) – 28 = 128 – 28 = 100
Где в первом действие нашли количество страниц, которые осталось прочитать во 2 и 3 день;
А во втором действии – сколько страниц осталось прочитать в 3 день.
Способ 3:
180 – (52 + 28) = (180 – 28) – 52 = 152 – 52 = 100
Где в первом действии нашли количество страниц, которые осталось прочитать в 1 и 3 день, а во втором действии – сколько осталось прочитать в 3 день.
В книге 180 страниц. В первый день ученик прочитал 52 страницы, во второй – 28 страниц. Сколько страниц ему осталось прочитать? Измени вопрос задачи так, чтобы получить ответ: на 20 страниц.
Ответ:Всего – 180 стр.
Прочитал – 52 стр. и 28 стр.
Осталось – ? стр.
1) 52 + 28 = 80 (стр.) – прочитал всего.
2) 180 − 80 = 100 (стр.) – осталось
Ответ: 100 страниц осталось прочитать.
Вопрос: На сколько страниц больше ему осталось прочитать, чем он уже прочитал?
100 – 80 = 20 (стр.) – на сколько больше ему осталось прочитать, чем он уже прочитал.
Ответ: на 20 страниц больше ему осталось прочитать, чем он уже прочитал.
Номер 9.
Ответ:
Вспомним названия компонентов действий сложения и вычитания, а также зависимости между компонентами и результатами этих действий:
1 слагаемое + 2 слагаемое = значение суммы.
Значение суммы – 1 слагаеоме = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Нахождение значений выражения сводится к применению правил:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы:
(а + в) – с = (а – с) + в.
Находим значения выражений, применяя правила/
180 + 230 = 180 + (220 + 10) = (180 + 220) + 10 = 400 + 10 = 410, по правилу прибавления суммы к числу.
430 – 70 = 430 – (30 + 40) = (430 – 30) – 40 = 400 – 40 = 360, по правилу вычитания суммы из числа.
120 – 40 = 120 – (20 + 20) = (120 – 20) – 20 = 100 – 20 = 80, по правилу вычитания суммы из числа.
150 – 50 = (100 + 50) – 50 = 100 + (50 – 50) = 100 + 0 = 100, по правилу вычитания числа из суммы.
90 – 90 = 0 , потому что если любое число вычесть из самого себя, то получится 0.
270 – 30 = (200 + 70) – 30 = 200 + (70 – 30) = 200 + 40 = 240, по правилу вычитания числа из суммы.
500 + 20 = 520
40 – 25 = 40 – (20 + 5) = (40 – 20) – 5 = 20 – 5 = 15, по правилу вычитания суммы из числа.
75 – 75 = 0, потому что если любое число вычесть из самого себя, то получится 0.
40 – 40 = 0, потому что если любое число вычесть из самого себя, то получится 0.
Заполняем таблицу.
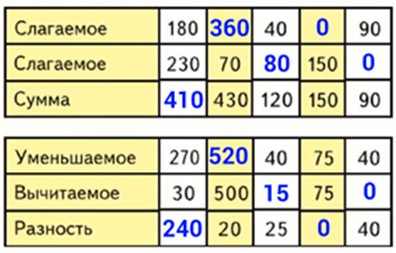
Номер 10.
Кто тяжелее: мишка или белочка – и на сколько граммов?

1) 200 ∙ 2 = 400 (г) – собачка тяжелее белочки.
2) 100 ∙ 3 = 300 (г) – мишка тяжелее собачки.
3) 400 + 300 = 700 (г) – мишка тяжелее белочки.
Ответ: мишка тяжелее белочки на 700 г.
Для того чтобы решить задачу, составь равенства по картинкам.
Помни, что весы могут многое сообщить о весе предметов, стоящих на чашах:
Чаши на одном уровне – вес предметов на чашах одинаковый.
Одна чаша находится выше другой – вес предмета на ней меньше.
Одна чаша находится ниже другой – вес предмета на ней больше.
Рассмотрим левую картинку и составим равенство.
Весы находятся в равновесии, поэтому запишем следующие равенство:
Собака = белка + 200 г + 200 г.
Собака = белка + 400 гр.
Следовательно, собака тяжелее белочки на 400 грамм.
Рассмотрим правую картинку и составим равенство.
Весы находятся в равновесии, поэтому запишем следующие равенство:
Собака + 100 г + 100 г + 100 г = мишка.
Собака + 300 г = мишка.
Следовательно, мишка тяжелее собаки на 300 грамм.
Рассуждаем.
Нам нужно сравнить вес белки и мишки, значит, выражаем вес собаки через вес белочки.
(Белка + 400 г) + 300г = мишка.
Получается, что на левой чаше весов: белка + 700 г, а на правой – мишка. При этом чаши находятся в равновесии, значит, белка на 700 грамм меньше мишки, а мишка на 700 грамм тяжелее белки.
Запишем решение и ответ.
1) 200 ∙ 2 = 400 (г) – собачка тяжелее белочки.
2) 100 ∙ 3 = 300 (г) – мишка тяжелее собачки.
3) 400 + 300 = 700 (г) – мишка тяжелее белочки.
Ответ: мишка тяжелее белочки на 700 г.
Задание внизу страницы
Ответ:396 < 936 529 < 592 748 < 848
Здание на сравнение чисел. Необходимо сравнить числа и поставить знак <, > или =.
Помни о том, как сравнивают трехзначные числа:
1) Сравнить, сколько знаков в числах. В большем числе количество знаков больше.
2) В случае, если количество знаков одинаковое, сравнивай количество единиц каждого разряда, начиная с высшего. Сравниваем количество сотен.
3) Если количество сотен одинаковое, сравниваем количество десятков.
4) Если количество десятков одинаковое, сравниваем единицы.
5) Делаем вывод о том, какое число больше.
Выполним сравнение
396 и 936
1) Оба числа трехзначные, т.е. в записи чисел – 3 знака.
2) Сравниваем количество сотен. В первом числе 3 сотни, а во втором – 9 сотен. 3 сот < 9 cот, значит, число 396 < 936.
Сравнение окончено, ставим знак: 396 < 936.
529 и 592
1) Оба числа трехзначные, т.е. в записи числа – 3 знака.
2) Сравниваем количество сотен. В первом числе 5 сотен и во втором – 5 сотен. Значит, количество сотен одинаковое.
3) Сравниваем количество десятков: в первом числе 2 десятка, а во втором – 9 десятков. 2 дес. < 9 дес., значит, число 529 < 592.
Сравнение окончено, ставим знак: 529 < 592.
748 и 848
1) Оба числа трехзначные, т.е. в записи чисел – 3 знака.
2) Сравниваем количество сотен. В первом числе 7 сотни, а во втором – 8 сотен. 7 сот < 8 cот, значит, число 748 < 848.
Сравнение окончено, ставим знак: 748 < 848.
Оформляем задание в тетрадь
396 < 936
529 < 592
748 < 848
Задание на полях страницы
Ребусы:

Ответ:

Вспомним компоненты действия сложения и их зависимости между собой:
Слагаемое + 2 слагаемое = значение суммы.
Значение суммы – 1 слагаемое = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Шаг 1.
Рассуждаем.
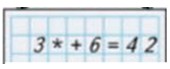
Нам неизвестно 1 слагаемое, чтобы найти 1 слагаемое нужно из суммы вычесть 2 слагаемое.
42 – 6 = 36
Вывод.
Нам известно, что в 1 слагаемое это 2-хзначное число, в котором 3 десятка. Найдя первое слагаемое, делаем вывод, что в записи пропущено 6 единиц.
Заполним пропуск.
36 + 6 = 42
Шаг 1.
Рассуждаем.

Во втором слагаемое количество единиц неизвестно. Чтобы узнать нужно из количества единиц значения суммы вычесть количество единиц 1 слагаемого.
Получаем, что 3 ед. – 7 ед., вычесть нельзя, поэтому, занимаем десяток.
13 ед. – 7 ед. = 6 ед.
Во 2 слагаемом – 6 единиц.
Рассуждаем.
В значении суммы количество десятков неизвестно. Чтобы узнать нужно сложить количество десятков первого и второго слагаемого. Тогда, 4 дес. + 1 дес. = 5 дес. да еще 1 дес. = 6 дес.
Заполним пропуски.
47 + 16 = 63
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.