Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 49

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 231.
Уроки начались в 9 ч и закончились через 4 ч. Пользуясь циферблатом, скажи, когда закончились эти уроки.
Решение: 9 + 4 = 13 (ч).
Составь задачи, которое решаются так:
13 − 4 = 9 (ч). 13 − 9 = 4 (ч).
Уроки длились 4 ч и закончились в 13 ч. Пользуясь циферблатом, скажи, когда начались эти уроки.
13 − 4 = 9 (ч) – время начала уроков.
Ответ: в 9 ч начались уроки.
Уроки начались в 9 ч и закончились в 13 ч. Пользуясь циферблатом, скажи, сколько длились эти уроки.
13 − 9 = 4 (ч) – длились уроки.
Ответ: 4 ч длились уроки.
Вспомни, как расположены цифры, обозначающие часы на циферблате. Используя их, ответь на вопросы.
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек.
1 час – 60 мин.
1 сут = 24 часа.
Составляем задачу по первому выражению.
13 – 4 = 9 (ч).
Маша пришла домой в 13 часов. 4 часа она провела на дне рождения подруги Сони. Во сколько часов начался День рождения Сони?
Оформляем условие в виде краткой записи.
Начало дня рождения – ? ч.
Длительность – 4 ч.
Окончание дня рождения – 13 ч.
Рассуждаем.
Чтобы узнать, когда начался день рождения Сони, нужно из времени окончания дня рождения вычесть длительность.
13 – 4 = 9 (ч) – начался день рождения Сони.
Записываем ответ.
Ответ: в 9 часов.
Составляем задачу по второму выражению.
13 – 9 = 4 (ч).
Папа Гены вернулся домой с работы в час дня. Смена длилась 9 часов. В какое время папа Гены ушел на работу?
Оформляем условие в виде краткой записи.
Начало смены – ? ч.
Продолжительность смены – 9 ч.
Окончание смены – 13 ч.
Рассуждаем.
Чтобы узнать, в какое время папа Гены ушел на работу, нужно из времени, когда смена закончилась вычесть продолжительность смены.
13 – 9 = 4 (ч) – утра началась смена.
Записываем ответ.
Ответ: 4 часа.
Номер 232.
Запиши решение каждой задачи.
1) Экскурсия по городу началась в 10 ч утра и закончилась в 12 ч 30 мин дня. Сколько времени продолжалась экскурсия? 2) Спектакль начался в 13 ч и продолжался 3 ч 15 мин. Когда закончился этот спектакль?
Ответ:Задача 1:
12 ч 30 мин – 10 ч = 2 ч 30 мин
Ответ: 2 ч 30 мин длилась экскурсия.
Задача 2:
13 ч + 3 ч 15 мин = 16 ч 15 мин
Ответ: в 16 ч 15 мин закончился спектакль.
Вспомни, как расположены цифры, обозначающие часы на циферблате. Используя их, ответь на вопросы.
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек.
1 час – 60 мин.
1 сут = 24 часа.
Шаг 1.
Рассуждаем.
Экскурсия по городу началась в 10 ч утра и закончилась в 12 ч 30 мин. Значит, чтобы узнать, сколько времени длилась экскурсия, нужно из времени окончания экскурсии вычесть время начала.
Рассмотрим данное условие задачи на часах.
Помни, что минуты вычитают из минут, а часы из часов.
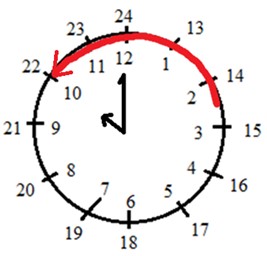
Решаем задачу.
12 ч 30 мин – 10 ч = 2 ч 30 мин.
Записываем ответ.
Ответ: 2 ч 30 мин – экскурсия.
Шаг 1.
Рассуждаем.
Спектакль начался в 13 ч и продолжался 3 часа 15 минут. Значит, чтобы узнать, во сколько закончился спектакль, нужно к времени начала спектакля прибавить его длительность.
Рассмотрим данное условие задачи на часах.
Помни, что единицы можно складывать с единицами, а десятки с десятками.
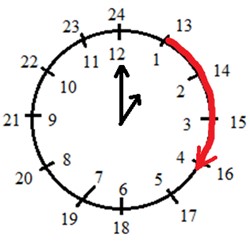
Решаем задачу.
13 ч + 3 ч 15 мин = 16 ч 15 мин.
Записываем ответ.
Ответ: 16 ч 15 мин – закончился спектакль.
Номер 233.
Дополни каждую задачу и реши ее.
1) В книге три рассказа. Они занимают 112 страниц. Первый рассказ занимает ☐ страниц, второй – на ☐ страниц больше, чем первый. Сколько страниц занимает третий рассказ?
2) Туристы были в пути 2 ч. Третью часть этого времени они затратили на переправу через реку, ☐ мин – на привал, а остальное время – на пеший переход. Сколько времени двигались туристы пешком? (Вырази часы в минутах.)
Задача 1:

1) 20 + 15 = 35 (стр.) – занимает второй рассказ.
2) 35 + 20 = 55 (стр.) – занимает второй и первый рассказ вместе.
3) 112 – 55 = 57 (стр.) – занимает третий рассказ.
Ответ: третий рассказ занимает всего 57 страниц.
Задача 2:
1) 2 часа = 120 минут
2) 120 : 3 = 40 (мин) – туристы переправлялись через реку.
3) 40 + 40 = 80 (мин) – туристы переправлялись и отдыхали.
4) 120 – 80 = 40 (мин) – туристы шли пешком.
Ответ: 40 минут.
«на 15 страниц больше», значит, вычисляется сложением.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Шаг 1.
Дополняем условие первой задачи.
В книге три рассказа. Они занимают 112 страниц. Первый рассказ занимает 20 страниц, второй – на 15 страниц больше, чем первый. Сколько страниц занимает третий рассказ?
Оформляем условие в виде краткой записи.

Рассуждаем.
Первый рассказ занимает 20 страниц, а второй – на 15 страниц больше. Значит, что второй рассказ занимает столько, сколько первый рассказ и еще 15 страниц. Получается, чтобы узнать, сколько страниц занимает второй рассказ, нужно к количество страниц первого рассказа прибавить 15 страниц.
1) 20 + 15 = 35 (стр.) – занимает второй рассказ.
Продолжаем рассуждение.
Мы узнали, что первый рассказ занимает 20 страниц, а второй – 25 страниц. Общее количество страниц первого и второго рассказа складывается из количества страниц обоих рассказов. Значит, чтобы узнать, сколько страниц занимает первый и второй рассказ, складываю количество страниц каждого. 2) 35 + 20 = 55 (стр.) – занимает второй и первый рассказ вместе.
Продолжаем рассуждение.
Общее количество страниц всех рассказов складывается из количество страниц каждого рассказа. Значит, чтобы узнать, сколько страниц в третьем рассказе, из общего количества страниц вычитаю количество страниц первого и второго рассказа.
3) 112 – 55 = 57 (стр.) – занимает третий рассказ.
Записываем ответ.
Ответ: 57 страниц.
Решение выражением: 112 – (20 + (20 + 15)).
Шаг 1.
Дополняем условие второй задачи.
Туристы были в пути 2 ч. третью часть этого времени они затратили на переправу через реку, 40 минут – на привал, а остальное время – на пеший переход. Сколько времени двигались туристы пешком?
Оформляем условие в виде краткой записи.

Рассуждаем.
Туристы были в пути 2 часа. Третью часть этого времени они затратили на переправу через реку. Третья часть, значит, одна из трех одинаковых частей. Поэтому общее время в пути делим на количество частей.
2 часа = 120 минут.
1) 120 : 3 = 40 (мин) – туристы переправлялись через реку.
Продолжаем рассуждение.
Мы узнали, что на переправу было потрачено 40 минут. общее время на переправу и привал складывается из времени, проведенного на переправе и привале. Значит, чтобы узнать, сколько времени туристы переправлялись и отдыхали, нужно сложить количество времени переправы и отдыха.
2) 40 + 40 = 80 (мин) – туристы переправлялись и отдыхали.
Продолжаем рассуждение.
Общее время в пути складывается из времени, которое туристы переправлялись, отдыхали и шли пешком. Значит, чтобы узнать, сколько времени туристы шли пешком, нужно из общего количество времени в пути вычесть время переправы и привала.
3) 120 – 80 = 40 (мин) – туристы шли пешком.
Записываем ответ.
Ответ: 40 минут.
Решение выражением: 120 – (120 : 30 + 40).
Номер 234.
Чему равна треть суток? половина суток? четверть часа? четверть года?
Ответ:Треть суток = 24 : 3 = 8 ч. Половина суток = 24 : 2 = 12 ч. Четверть часа = 60 : 4 = 15 мин. Четверть года = 12 : 4 = 3 мес.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Сутки длятся 24 часа.
Треть суток – третья часть, значит, чтобы узнать, сколько часов в третьей части суток, нужно длительность суток разделить на 3.
Тогда, 24 ч. : 3 = 8ч.
Продолжаем рассуждение.
Половина суток – одна вторая часть, значит, чтобы узнать, сколько часов в половине суток, нужно длительность суток разделить на 2.
Тогда, 24 ч. : 2 = 12 ч.
Продолжаем рассуждение.
Четверть часа – четвертая часть, значит, чтобы узнать, сколько минут в четверти часа, нужно количество минут в часе разделить на 4.
Тогда, 60 : 4 = 15 мин.
Продолжаем рассуждение.
Год – 12 мес.; четверть года – четвертая часть года, значит, чтобы узнать, сколько часов в четвертой части года, нужно длительность года разделить на 4.
Тогда, 12 мес. : 4 = 3 мес.
Оформляем задание в тетрадь.
Треть суток – 24 : 3 = 8 ч.
Половина суток – 24 : 2 = 12 ч.
Четверть часа – 60 : 4 = 15 мин.
Четверть года – 12 : 4 = 3 мес.
Номер 235.
Чему равна одна пятая часть сантиметра? одна десятая часть квадратного сантиметра?
Ответ:Одна пятая см = 10 : 5 = 2 мм Одна десятая см2 = 100 : 10 = 10 мм2
Вспомним о соотношении числовых значений единиц измерения длины:
1 см – 10 мм.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
1 см – 10 мм; пятая часть – одна пятая, значит, чтобы узнать, какова пятая часть сантиметра, нужно 1 см : 5, тогда, 10 мм : 5 = 2 мм.
Продолжаем рассуждение.
1 см2 – это 100 мм2; десятая часть – одна десятая, значит, чтобы узнать, сколько мм2 в десятой части см2, нужно 100 мм2 : 10 = 10 мм2.
Оформляем задание в тетрадь.
Одна пятая см – 10 : 5 = 2 мм.
Одна десятая см2 – 100 : 10 = 10 мм2.
Номер 236.
Фермер собрал 8 т моркови, а свёклы – на 4 т больше. Половину моркови и четвёртую часть свёклы переработали на сок, а оставшиеся овощи увезли в магазины. Составь по этому условию различные выражения и поясни их значения.
Ответ:1) 8 + 4 – число тонн свёклы. 2) 8 + (8 + 4) – число тонн моркови и свёклы. 3) 8 : 2 + (8 + 4) : 4 – переработанных на сок. 4) (8 + (8 + 4)) – (8 : 2 + (8 + 4) : 4) – количество овощей в магазин.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Составляем первое выражение.
Фермер собрал 8 т моркови, а свёклы – на 4 тонны больше. Значит, что свёклы собрали столько, сколько моркови и еще 4 тонны. Получается, чтобы узнать, сколько тонн свёклы собрали, нужно к количество моркови прибавить 4 тонны.
Выражение для вычисления количество привезенной свёклы:
8 + 4.
Составляем второе выражение.
Общее количество привезенной моркови и свеклы складывается из количества привезенной моркови и свёклы. Поэтому, чтобы узнать, сколько тон моркови и свёклы было собрано, складываю количество собранных овощей.
Выражение для вычисления количества собранных овощей:
8 + (8 + 4), где 8 + 4 – количество собранной свёклы.
Составляем третье выражение.
Половину моркови переработали в сок. Половина – одна вторая. Значит, чтобы узнать, сколько всего моркови переработали в сок, нужно общее количество моркови разделить на 2.
Выражение для вычисления количества моркови, переработанной в сок:
8 : 2.
Составляем четвертое выражение.
Четвертую часть свёклы переработали в сок. Четвертая часть, значит, одна четвертая. Поэтому, чтобы узнать, сколько свёклы переработали на сок, общее количество свёклы делю на 4.
Выражение для вычисления количества свёклы, переработанной в сок:
(8 + 4) : 4.
Составляем пятое выражение.
Общее количество сока складывается из количества переработанного сока свёклы и моркови. Значит, чтобы узнать, сколько сока всего получилось, нужно сложить количество сока моркови свеклы.
Выражение для вычисления количества сока:
(8 : 2) + (8 + 4) : 4.
Составляем шестое выражение.
Общее количество овощей складывается из количества овощей, которые пошли на сок и в магазин. Значит, чтобы узнать, сколько овощей пошло на продажу, из общего количества овощей вычитаю количество тех, что пошли на сок.
Выражение для вычисления количества овощей, отправленных в магазин:
8 + 4 – (8 : 2 + ((8 + 4) : 4)).
Номер 237.
Выпиши отдельно названия тупых, острых и прямых углов с вершиной в точке В. Назови каждый треугольник.

Углы с вершиной В: Тупой угол – АВС или DВС. Острый угол – АВМ или DBO, DBM, ABO. Прямой угол – МВС. Треугольники – АВС, МВС, DBC, ADC, МОС, ОВС, ВОD.
Вспомним, что выделяют разные виды углов по их градусной мере:
Прямой угол – угол, градусная мера которого равна 90 градусам.
Острый угол – угол, градусная мера которого меньше 90 градусов.
Тупой угол – угол, градусная мера которого больше прямого угла, но меньше развернутого.
Найдем все углы и треугольники на рисунке в учебнике.
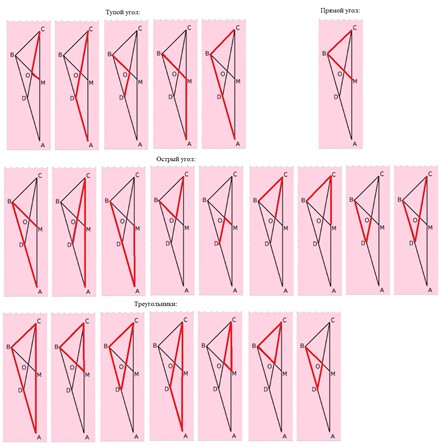
Оформим задание в тетрадь.
Тупой угол – АВС, ВОD, СDА, ВМА, МОС.
Острый угол – АВМ, СОВ, СМО, САВ, СDВ, ВСА, ВСD.
Прямой угол – МВС.
Треугольники – АВС, МВС, DBC, ADC, МОС, ОВС, ВОD.
Номер 238.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления.
700 – 348 : 4 · 6 = 178
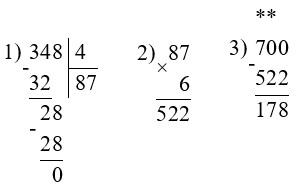
696 – 612 : 6 : 3 = 662
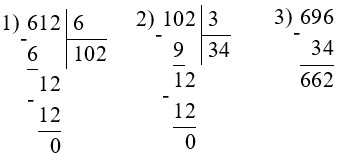
900 – (600 – 130 · 4) : 10 = 892
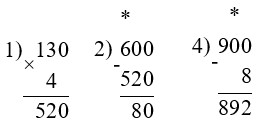
3) 80 : 10 = 8
800 – 250 + 140 : 5 · 2 = 606
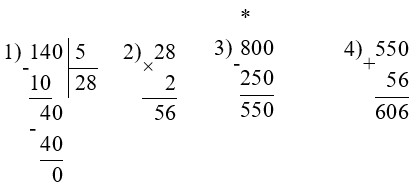
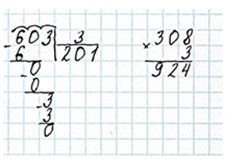
Оформляем задание в тетрадь.

Задание внизу страницы.
Детский утренник закончился в 14 ч. Когда начался этот утренник, если он продолжался 1 ч?
Ответ:14 – 1 = 13 ч – начало утренника.
Ответ: утренник начался в 13 часов.
Вспомни, как расположены цифры, обозначающие часы на циферблате. Используя их, ответь на вопросы.
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек.
1 час – 60 мин.
1 сут = 24 часа.
Рассуждаем.
Детский утренник закончился в 14 часов. Он продолжался 1 час. Значит, чтобы узнать, во сколько утренник начался, нужно из времени окончания утренника вычесть его длительность.
Рассмотрим данное условие задачи на часах.
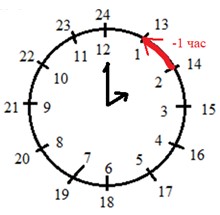
Решаем задачу.
14 – 1 = 13 (ч) – начало утренника.
Записываем ответ.
Ответ: в 13 часов.
Номер 237.
Уроки начались в 9 ч и закончились через 4 ч. Пользуясь циферблатом, скажи, когда закончились эти уроки. Запиши решение задачи.
Составь задачи, которое решаются так.
13 – 4 = 9 (ч) 13 − 9 = 4 (ч).
9 + 4 = 13 (ч) – закончились уроки.
Ответ: уроки закончились в 13 часов.
1) Уроки длились 4 ч и закончились в 13 ч. Пользуясь циферблатом, скажи, когда начались эти уроки.
13 – 4 = 9 (ч) – время начала уроков.
Ответ: уроки начались в 9 ч.
2) Уроки начались в 9 ч и закончились в 13 ч. Пользуясь циферблатом, скажи, сколько длились эти уроки.
13 – 9 = 4 (ч) – длились уроки.
Ответ: уроки длились всего 4 ч.
Номер 238.
Запиши решение каждой задачи.
1) Экскурсия по городу началась в 10 ч утра и закончилась в 12 ч 30 мин дня. Сколько времени продолжалась экскурсия? 2) Спектакль начался в 13 ч и продолжался 3 ч 15 мин. Когда закончился этот спектакль?
Ответ:Задача 1:
12 ч 30 мин – 10 ч = 2 ч 30 мин
Ответ: экскурсия длилась всего 2 ч 30 мин.
Задача 2:
13 ч + 3 ч 15 мин = 16 ч 15 мин
Ответ:спектакль закончился в 16 ч 15 мин.
Номер 239.
Дополни каждую задачу и реши ее.
1) В книге три рассказа. Они занимают 112 страниц. Первый рассказ занимает ☐ страниц, второй – на ☐ страниц больше, чем первый. Сколько страниц занимает третий рассказ? 2) Туристы были в пути 2 ч. Третью часть этого времени они затратили на переправу через реку, ☐ мин – на привал, а остальное время – на пеший переход. Сколько времени двигались туристы пешком? (Вырази часы в минутах.)
Ответ:Задача 1:

1) 20 + 15 = 35 (стр.) – занимает второй рассказ.
2) 35 + 20 = 55 (стр.) – занимает второй и первый рассказ вместе.
3) 112 – 55 = 57 (стр.) – занимает третий рассказ.
Ответ: 57 страниц всего занимает третий рассказ.
Задача 2:
1) 2 часа = 120 минут
2) 120 : 3 = 40 (мин) – туристы переправлялись через реку.
3) 40 + 40 = 80 (мин) – туристы переправлялись и отдыхали.
4) 120 – 80 = 40 (мин) – туристы шли пешком.
Ответ: 40 минут всего туристы шли пешком.
Номер 240.
Чему равна треть суток? половина суток? четверть часа? четверть года?
Ответ:Треть суток = 24 : 3 = 8 ч Половина суток = 24 : 2 = 12 ч Четверть часа = 60 : 4 = 15 мин Четверть года = 12 : 4 = 3 мес.
Номер 241.
Чему равна одна пятая часть сантиметра? одна десятая часть квадратного сантиметра?
Ответ:Одна пятая см = 10 : 5 = 2 мм Одна десятая см2 = 100 : 10 = 10 мм2
Номер 242.
Фермер собрал 8 т моркови, а свёклы – на 4 т больше. Половину моркови и четвёртую часть свёклы переработали на сок, а оставшиеся овощи увезли в магазины. Составь по этому условию различные выражения и поясни их значения.
Ответ:1) 8 + 4 – число тонн свёклы. 2) 8 + (8 + 4) – число тонн моркови и свёклы. 3) 8 : 2 + (8 + 4) : 4 – переработанных на сок. 4) (8 + (8 + 4)) − (8 : 2 + (8 + 4) : 4) – количество овощей в магазин.
Номер 243.
Выпиши отдельно названия тупых, острых и прямых углов с вершиной в точке В. Назови каждый треугольник.

Углы с вершиной В: Тупой угол – АВС или DВС. Острый угол – АВМ или DBO, DBM, ABO. Прямой угол – МВС. Треугольники – АВС, МВС, DBC, ADC, МОС, ОВС, ВОD.
Номер 244.
Ответ:
Задание внизу страницы.
Детский утренник закончился в 14 ч. Когда начался этот утренник, если он продолжался 1 ч?
Ответ:14 – 1 = 13 ч – начало утренника.
Ответ: утренник начался в 13 часов.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.