Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 19

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 12.
Ответ:1)

2)

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помним, что вычислить сумму нескольких слагаемых можно разными способами. Мы будем использовать 2 способ.

Вычисляем значение суммы сразу трех слагаемых так: количество единиц значения суммы складывается из суммы количества единиц всех слагаемых. Аналогично с десятками и сотнями.
Расставляем порядок действий и выполняем вычисления.
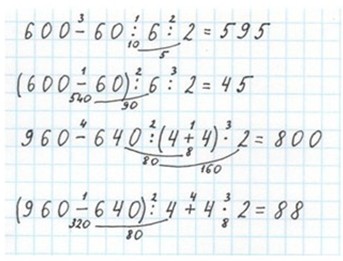
Выполняем письменное сложение.

Оформляем задание в тетрадь.
Номер 13.
Для школьной мастерской купили рубанки, отвёртки и молотки. Рубанков 36 штук, отвёртки составляли третью часть числа рубанков, а молотков было в 4 раза больше, чем отвёрток. Объясни, что обозначают выражения:
Ответ:36 : 3 – число отвёрток. 36 : 3 + 36 – число рубанков и отвёрток. 36 : 3 ∙ 4 – число молотков. 36 + 36 : 3 ∙ 4 – число рубанков и молотков.
Доля – одна часть из тех, на которые разделили целое.
Пр: целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
«в 4 раза больше», значит, вычисляется умножением.
Оформляем условие в виде краткой записи.

Рассуждаем.
Рубанков купили 36 штук, а отверток – третья часть рубанков. Значит, что количество рубанков разделили на 3, а взяли одну часть, т.е. отверток привезли в 3 раза меньше, чем рубанков. Поэтому, чтобы узнать, сколько отверток привезли, нужно количество рубанков разделить на 3.
36 : 3 – число отвёрток.
Продолжаем рассуждение.
Молотков привезли в 4 раза больше, чем отверток. Значит, чтобы узнать, сколько молотков привезли, нужно количество отверток умножить на 4.
36 : 3 + 36 – число рубанков и отвёрток.
Продолжаем рассуждение.
Общее количество рубанков и молотков складывается из количества каждого инструмента. Значит, чтобы узнать, сколько привезли рубанков и молотков, нужно сложить количества каждого из инструментов. 36 : 3 ∙ 4 – число молотков.
Продолжаем рассуждение.
Общее количество рубанков и отверток складывается из количества обоих видом инструментов. Значит, чтобы узнать, сколько рубанков и отверток привезли, нужно сложить количества обоих видов инструментов.
36 + 36 : 3 ∙ 4 – число рубанков и молотков.
Номер 14.
В одной теплице собрали 38 кг помидоров, в другой – 50 кг. Все эти помидоры разложили в ящики, по 8 кг в каждый. Сколько таких ящиков потребовалось? Измени числа так, чтобы задача решалась двумя способами. Сравни эти способы решения.
Ответ:
1) 38 + 50 = 88 (кг) – было всего помидоров.
2) 88 : 8 = 11 (ящ.)
Ответ: 11 ящиков потребовалось для раскладки помидоров.
Для того, чтобы задача решалась двумя способами надо чтобы число килограммов помидоров, собранных в каждой теплице делилось на 8. Также очень важно, чтобы сохранялось количество килограмм всего урожая.
Значит сумма помидоров в первой и второй теплице – 88 кг.
Если в одном ящике 48 кг, то в другом 88 − 48 = 40 кг.
В одной теплице собрали 48 кг помидор, а в другой 40. Затем все помидоры разложили в ящики, по 8 кг в каждый. Сколько ящиков потребовалось?
1) 48 : 8 = 6 (ящ.) – для первого парника.
2) 40 : 8 = 5 (ящ.) – для второго парника.
3) 6 + 5 = 11 (ящ.) – потребовалось для всего урожая.
Ответ: 11 ящиков потребовалось для раскладки помидоров.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Кол-во помидоров 1 ящика · кол-во ящиков = общее кол-во помидоров.
Общее кол-во помидоров : кол-во ящиков = кол-во п. в 1 ящике.
Общее кол-во помидоров : кол-во п. в 1 ящике = кол-во ящиков.
Оформляем условие в виде таблицы.

Рассуждаем.
Общее количество помидоров складывается из количества помидоров в каждом ящике. Значит, чтобы узнать, сколько помидоров было собрано, нужно сложить количество помидоров каждого ящика.
1) 38 + 50 = 88 (кг) – было всего помидоров.
Продолжаем рассуждение.
Из таблицы видно, что общее количество помидоров складывается из количества помидоров каждого ящика. Значит, чтобы узнать, сколько ящиков потребовалось, нужно общее количество ящиков разделить на массу 1 ящика.
2) 88 : 8 = 11 (ящ.).
Записываем ответ.
Ответ: 11 ящиков потребовалось.
Изменим числа в задаче.
Для того, чтобы задача решалась двумя способами надо чтобы число килограммов помидоров, собранных в каждой теплице делилось на 8. Также очень важно, чтобы сохранялось количество килограмм всего урожая.
Значит сумма помидоров в первой и второй теплице – 88 кг.
Если в одном ящике 48 кг, то в другом 88 – 48 = 40 кг.
Получаем новое условие и сравниваем решения.
«В одной теплице собрали 48 кг помидор, а в другой 40. Затем все помидоры разложили в ящики, по 8 кг в каждый. Сколько ящиков потребовалось?»
1-й способ решения:
(38 + 50) : 8 = 11 (ящ.).
2-й способ решения:
(48 : 8) + (40 : 8) = 11 (ящ.).
Номер 15.
1) Ученик затратил на решение задачи 6 мин, а на решение каждого из 8 примеров по 3 мин. Сколько всего времени затратил ученик на выполнение этого домашнего задания? 2) Заметь по часам и запиши, сколько времени тебе потребовалось на выполнение домашнего задания по математике.
Ответ:Задача – 6 мин
Примеры – 8 пр. по 3 мин
Всего – ? мин
1) 3 ∙ 8 = 24 (мин) – на решение примеров.
2) 24 + 6 = 30 (мин)
Ответ: 30 минут затратил на все задания.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Время на 1 пример · кол-во примеров = общее время решения.
Общее время решения : кол-во примеров = время на 1 пример.
Общее время решения : время на 1 пример = кол-во примеров.
Оформляем условие в виде краткой записи.
Задача – 6 мин.
Примеры – 8 пр. по 3 мин.
Всего – ? мин.
Рассуждаем.
Количество времени, затрачиваемое на решение каждого примера одинаковое. Чтобы узнать, сколько времени было затрачено всего, нужно время решения 1 примера умножаю на количество примеров.
1) 3 ∙ 8 = 24 (мин) – на решение примеров.
Продолжаем рассуждение.
Время выполнения всего домашнего задания складывается из времени выполнения каждого из заданий: задачи и примеров. Значит, чтобы узнать, сколько времени потратил ученик на выполнение заданий, нужно сложить время решения задачи и примеров.
2) 24 + 6 = 30 (мин).
Записываем ответ.
Ответ: 30 минут затратил на все задания.
Решение выражением: 6 + (3 · 8) = 30 (мин).
Номер 16.
Разбей знаки (буквы) на 2 группы.
Ответ:
М Ж Х Ш — можно провести ось симметрии. Б Щ Ц Г — нельзя провести ось симметрии.
Рассмотрим буквы(знаки), как геометрические объекты.
Ось симметрии – прямая относительно которой расположены одинаковые части фигуры или сами фигуры.
Рассмотрим знаки.
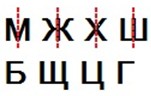
Сделаем вывод.
В буквах: М Ж Х Ш – можно провести ось симметрии.
В буквах: Б Щ Ц Г – нельзя провести ось симметрии.
Номер 1.
Как можно получить число, которое следует при счёте сразу за любым данным числом?
Ответ:Прибавить к числу единицу.
Вспомним свойства натурального ряда чисел. Несколько из них помогут для формулировки ответа на вопрос.
Натуральные числа – числа, которые используют при счете предметов (1, 2, 3 и т.д.).
Вспомним свойства натурального ряда чисел.
1) Ряд натуральных чисел имеет начало, но не имеет конца.
2) Между двумя соседними натуральными числами нет другого натурального числа.
3) Если к любому натуральному числу прибавить единицу, то получится число следующее за данным, т.е. т которое мы называем при счете после данного.
4) Если из любого натурального числа вычесть единицу, то получится число предыдущее, то, которое мы называем при счете перед данным.
Делаем вывод.
Чтобы получить число, которое следует при счёте сразу за любым данным числом, нужно прибавить к числу единицу.
Номер 2.
Прочитай, заполняя пропуски.
Ответ:10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот. = 1 тыс.
1 сот. = 100 ед.
1 сот. = 10 дес.
1 тыс. = 1000 ед.
1 тыс. = 100 дес.
1 тыс. = 10 сот.
Помним о том, что 10 единиц низшего разряда образует 10 единиц высшего.
Прочитаем и заполним пропуски.
10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот. = 1 тыс.
1 сот. = 100 ед, потому что 1 сот. – 10 дес., а 10 дес. – 10 ед. 10 · 10 = 100
1 сот. = 10 дес. ед, потому что 10 дес. · 1 = 10 дес. = 100
1 тыс. = 1000 ед,
потому что 1 тыс. – это 10 сот. а 1 сот. – это 100, тогда, 100 · 10 = 1000
1 тыс. = 100 дес.,
потому что 1 тыс. – это 10 сот, а 1 сот – это 10 дес. 10 · 10 = 100
1 тыс. = 10 сот, потому что, 100 · 10 = 1000
Оформим задание в тетрадь.
Номер 3.
Как по разному можно прочитать выражения?
Ответ:Сумма 320 и 40; 320 плюс 40; 320 увеличить на 40. Разность 470 и 300; 470 минус 300; 470 уменьшить на 300. Произведение 80 и 5; 80 умножить на 5; 80 увеличить в 5 раз. Частное 900 и 3; 900 поделить на 3; 900 уменьшить в 3 раза.
Сложение – слагаемое – сумма – знак плюс.
Вычитание – разность – знак минус.
Умножение – умножить – значение произведения.
Деление – разделить – значение частного.
Рассмотрим выражение.
320 + 40
470 – 300
80 · 5
900 : 3
Прочитаем выражения по-разному.
Сумма 320 и 40; 320 плюс 40; 320 увеличить на 40.
Разность 470 и 300; 470 минус 300; 470 уменьшить на 300.
Произведение 80 и 5; 80 умножить на 5; 80 увеличить в 5 раз.
Частное 900 и 3; 900 поделить на 3; 900 уменьшить в 3 раза.
Номер 4.
Объясни, в каком порядке должны выполняться действия по схематическим записям.
Ответ:
Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассмотрим каждый случай и расставим порядок действий.

Объясним 1 выражение.
Скобки отсутствуют. Выражение состоят из знаков одного уровня поэтому выполняются слева направо по порядку.
Объясним 2 выражение.
Скобки отсутствуют. Выражение состоят из знаков одного уровня поэтому выполняются слева направо по порядку.
Объясним 3 выражение.
Скобки отсутствуют. Выражение состоят из знаков разного уровня, поэтому выполняются сначала действия умножения и деления слева направо, а затем оставшиеся сложение и вычитанием слева направо, как записаны.
Объясним 4 выражение.
В выражении есть скобки. Сначала выполняются действия в них. Помимо них в скобках есть знаки действий одного уровня, поэтому они выполняются по порядку, как расположены слева направо.
Объясним 5 выражение.
В выражении есть две скобки, поэтому действия в них выполняются по порядку, как расположены скобки. Далее в выражении есть знаки арифметических действий одного уровня, поэтому оставшиеся действия выполняются слева направо как записаны.
Объясним 6 выражение.
В выражении есть скобки, поэтому сначала действия будут выполняться в них. При этом в скобках есть знаки действий разного уровня. Значит, сначала выполняются действие умножения, а потом - вычитания. Вне скобок есть знаки действий одного уровня. Значит, действия выполняются слева направо, как расположены.
Объясним 7 выражение.
В выражении есть скобки, поэтому сначала действия будут выполняться в них. При этом в скобках есть знаки действий разного уровня. Значит, сначала выполняется действие деления, а потом – сложения. Вне скобок есть знаки действий разного уровня. Значит, сначала выполняются деление, а потом вычитание.
Объясним 8 выражение.
В выражении есть скобки, поэтому сначала действия будут выполняться в них. Вне скобок есть знаки действий одного уровня. Значит, действия выполняются по порядку, как записаны.
Задание на полях страницы.
Ребус.

999 + 1 = 1000
Рассмотрим ребус. Звездочки обозначают знаки в записи чисел. Подумайте, когда такое может быть.
Рассмотрим ребус.
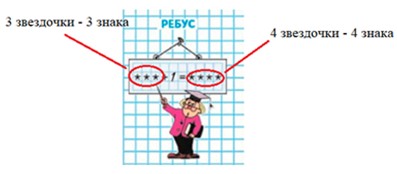
3 знака обозначают, что в числе 3 разряда: единицы, Десятки, сотни.
4 звездочки говорят о том, что в числе уже 4 разряда: единицы, десятки. сотни и тысячи.
Рассждаем.
Произошло образование еще одного разряда, когда 10 единиц одного разряда образуют одну единицу высшего.
К наибольшему трехзначному прибавили единицу и получили наименьшее четырехзначное.
Получаем выражение.
999 + 1 = 1000
Задание внизу страницы
Номер 12.
1) 600 – 60 : 6 : 2
(600 – 60) : 6 : 2
960 – 640 : (4 + 4) · 2
(960 – 640) : 4 + 4 · 2
2) 176 + 218 + 206
295 + 217 + 488
1)

2)

Номер 13.
Для спортивных секций купили теннисные, футбольные и волейбольные мячи. Теннисных мячей было 240, футбольные мячи составляли третью часть теннисных, а волейбольных мячей было в 4 раза меньше, чем футбольных. Объясни, что обозначают выражения.
240 : 3 240 : 3 + 240 240 : 3 : 4 240 + 240 : 3 : 4
Ответ:240 : 3 = 80 – количество футбольных мячей; 240 : 3 + 240 = 80 = 240 = 320 – количество теннисных и футбольных мячей вместе; 240 : 3 : 4 = 80 : 4 = 20 – количество волейбольных мячей; 240 + 240 : 3 : 4 = 240 + 20 = 260 – количество теннисных и волейбольных мячей вместе. /p>
Номер 14.
В одной теплице собрали 38 кг помидоров, в другой – 50 кг. Все эти помидоры разложили в ящики, по 8 кг в каждый. Сколько таких ящиков потребовалось? Измени числа так, чтобы задача решалась двумя способами. Сравни эти способы решения.
Ответ:
1) 38 + 50 = 88 (кг) – было всего помидоров.
2) 88 : 8 = 11 (ящ.)
Ответ: 11 ящиков потребовалось для раскладки помидоров.
Для того, чтобы задача решалась двумя способами надо чтобы число килограммов помидоров, собранных в каждой теплице делилось на 8. Также очень важно, чтобы сохранялось количество килограмм всего урожая.
Значит сумма помидоров в первой и второй теплице – 88 кг.
Если в одном ящике 48 кг, то в другом 88 – 48 = 40 кг.
В одной теплице собрали 48 кг помидор, а в другой 40. Затем все помидоры разложили в ящики, по 8 кг в каждый. Сколько ящиков потребовалось?
1) 48 : 8 = 6 (ящ.) – для первого парника.
2) 40 : 8 = 5 (ящ.) – для второго парника.
3) 6 + 5 = 11 (ящ.) – потребовалось для всего урожая.
Ответ: 11 ящиков потребовалось для раскладки помидоров.
Номер 15.
1) Ученик затратил на решение задачи 6 мин, а на решение каждого из 8 примеров по 3 мин. Сколько всего времени затратил ученик на выполнение этого задания? На какой вопрос отвечает решение: 3 ∙ 8 – 6?
2) Заметь по часам и запиши, сколько времени тебе потребовалось на выполнение домашнего задания по математике.
1) Задача – 6 мин
Примеры – 8 пр. по 3 мин
Всего – ? мин
1) 3 ∙ 8 = 24 (мин) – на решение примеров.
2) 24 + 6 = 30 (мин)
Ответ: 30 минут затратил на все задания.
3 ∙ 8 – 6 = 24 – 6 = 18 – на сколько дольше ученик решал примеры, чем задачу.
2) Запиши время, когда начал делать домашнее задание. А потом запиши время, когда закончил делать задания по математике. Из времени, когда закончил делать задания вычти время, когда начал делать и получится время выполнения домашнего задания.
Например:
17 : 20 – время начала выполнения домашнего задания
18: 00 — время окончания выполнения домашнего задания
18 ч 00 мин – 17 ч 20 мин = 17 ч 60 мин – 17 ч 20 мин = 40 мин – время выполнения домашнего задания.
Номер 16.
Разбей знаки (буквы) на 2 группы.
Ответ:
М Ж Х Ш – можно провести ось симметрии. Б Щ Ц Г – нельзя провести ось симметрии.
Номер 1.
Как можно получить число, которое следует при счёте сразу за любым данным числом?
Ответ:Прибавить к числу единицу.
Номер 2.
Прочитай, заполняя пропуски.
Ответ:10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот. = 1 тыс.
1 сот. = 100 ед.
1 сот. = 10 дес.
1 тыс. = 1000 ед.
1 тыс. = 100 дес.
1 тыс. = 10 сот.
Номер 3.
Как по разному можно прочитать выражения?
Ответ:Сумма 320 и 40; 320 плюс 40; 320 увеличить на 40. Разность 470 и 300; 470 минус 300; 470 уменьшить на 300. Произведение 80 и 5; 80 умножить на 5; 80 увеличить в 5 раз. Частное 900 и 3; 900 поделить на 3; 900 уменьшить в 3 раза.
Номер 4.
Объясни, в каком порядке должны выполняться действия по схематическим записям.
Ответ:
Задание на полях страницы
Ребус.

999 + 1 = 1000
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.