Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 83
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 2 часть. 3 класс - Учебник. Моро. Страница 83. Год 2024")
Закончи вычисления с объяснением.
Ответ:1-й способ решения:
240 ∙ 3 = 24 дес. ∙ 3 = 72 дес.
240 ∙ 3 = (200 + 40) ∙ 3 = 200 ∙ 3 + 40 ∙ 3 = 720
203 ∙ 4 = (200 + 3) ∙ 4 = 200 ∙ 4 + 3 ∙ 4 = 812
960 : 3 = 96 дес. : 3 = 32 дес.
960 : 3 = (900 + 60) : 3 = 900 : 3 + 60 : 3 = 300 + 20 = 320
960 : 6 = 96 дес. : 6 = 16 дес.
960 : 6 = (600 + 360) : 6 = 600 : 6 + 360 : 6 = 100 + 60 = 160
2-й способ решения:
240 · 3 = 24 дес. · 3 = 72 дес. = 720
203 · 4 = (200 + 3) · 4 = 2 сот. · 4 + 3 · 4 = 8 сот. + 12 = 800 + 12 = 812
960 : 3 = 96 дес. : 3 = 32 дес. = 320
960 : 6 = 96 дес. : 6 = 16 дес. = 160
Номер 1.
Вычисли с устным объяснением.
Ответ:303 ∙ 2 = (300 + 3) ∙ 2 = 300 ∙ 2 + 3 ∙ 2 = 600 + 6 = 606
205 ∙ 3 = (200 + 5) ∙ 3 = 200 ∙ 3 + 5 ∙ 3 = 615
120 ∙ 4 = (100 + 20) ∙ 4 = 400 + 80 = 480
230 ∙ 3 = (200 + 30) ∙ 3 = 200 ∙ 3 + 30 ∙ 3 = 690
42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 14
420 : 3 = (300 + 120) : 3 = 300 : 3 + 120 : 3 = 140
560 : 4 = (400 + 160) : 4 = 400 : 4 + 160 : 4 = 140
840 : 7 = (700 + 140) : 7 = 700 : 7 + 140 : 7 = 120
Номер 2.
Уменьши в 10 раз числа: 560, 690, 700. Полученные числа увеличь на 100.
Ответ:560 : 10 = 56
690 : 10 = 69
700 : 10 = 70
56 + 100 = 156
69 + 100 = 169
70 + 100 = 170
Номер 3.
Ежедневно на поливку грядок расходовали утром 6 ведер воды, а вечером 9 ведер. Сколько ведер воды израсходовали на поливку грядок за неделю? Реши задачу двумя способами.
Ответ:
1-й способ решения:
1) 6 + 9 = 15 (в.) – расходовали ежедневно.
2) 15 ∙ 7 = 105 (в.) – за неделю.
Ответ: 105 вёдер воды израсходовали на полив грядок за неделю.
2-й способ решения:
1) 6 ∙ 7 = 42 (в.) – расходовали утром.
2) 9 ∙ 7 = 63 (в.) – расходовали вечером.
3) 42 + 63 = 105 (в.) – всего за неделю.
Ответ: 105 вёдер воды израсходовали на полив грядок за неделю.
При автоматическом поливе грядок утром расходовали 60 л воды, а вечером – 80 л. Сколько литров израсходовали на полив грядок за неделю? Реши задачу. Измени вопрос задачи так, чтобы в задаче был ответ: на 140 л.
Ответ:
1) 60 + 80 = 6 дес. + 8 дес. = 14 дес. = 140 (л) – воды расходовали ежедневно.
2) 140 · 7 = 14 дес. · 7 = (10 + 4) дес. · 7 = (70 + 28) дес. = 98 дес. = 980 (л) – воды израсходовали за неделю.
Ответ: 980 литров воды израсходовали за неделю.
Составим следующий вопрос: «На сколько больше литров воды израсходовали по вечерам, чем по утрам, в течении всей недели?»
1) 60 · 7 = 6 дес. · 7 = 42 дес. = 420 (л) – воды израсходовали по утрам;
2) 80 · 7 = 8 дес. · 7 = 56 дес. = 560 (л) – воды израсходовали по вечерам.
3) 560 – 420 = 56 дес. – 42 дес. = 14 дес. = 140 (л) – на столько больше воды.
Ответ: на 140 л воды больше израсходовали по вечерам, чем по утрам.
1) Вспомни, как выполняют умножение и деление трёхзначных чисел, которые оканчиваются нулями.
2) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
3) Помни, что 1 неделя = 7 дней.
4) Помни, что 10 = 1 дес.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Узнаем, сколько всего литров воды расходовали за весь день.
Для этого нужно сложить количество воды, которое расходовали утром и вечером.
60 + 80 = 6 дес. + 8 дес. = 14 дес. = 140 (л) – воды расходовали ежедневно.
Продолжаем рассуждение.
Чтобы узнать общее количество израсходованной воды, нужно количество воды, израсходованное за весь день, умножить на количество дней.
140 ∙ 7 = 14 дес. ∙ 7 = (10 + 4) дес. ∙ 7 = (70 + 28) дес. = 98 дес. = 980 (л) – воды израсходовали за неделю.
Записываем ответ.
Ответ: 980 литров воды израсходовали за неделю.
Изменим вопрос.
Нужно изменить вопрос так, чтобы ответ был: на 140 л.
Составим следующий вопрос: «На сколько больше литров воды израсходовали по вечерам, чем по утрам, в течении всей недели?»
Решим задачу и сопоставим ответы.
Рассуждаем.
Чтобы узнать, сколько всего литров воды расходовали по утрам или вечерам в течении недели, нужно количество воды, которое расходовали утром или вечером, умножить на количество дней.
1) 60 ∙ 7 = 6 дес. ∙ 7 = 42 дес. = 420 (л) – воды израсходовали по утрам;
2) 80 ∙ 7 = 8 дес. ∙ 7 = 56 дес. = 560 (л) – воды израсходовали по вечерам.
Продолжаем рассуждение.
Чтобы узнать, на сколько больше воды израсходовали по вечерам, чем по утрам, нужно из количества воды, израсходованной по вечерам, вычесть количество воды, израсходованной по утрам.
560 – 420 = 56 дес. – 42 дес. = 14 дес. = 140 (л) – на столько больше воды.
Сравниваем ответы.
Мы получили ответ: на 140 л воды больше израсходовали по вечерам, чем по утрам.
Наш ответ совпадаем с условиями задачи, значит вопрос задан верно.
Номер 4.
Дедушка купил 5 одинаковых пакетов с картофелем, общая масса которых 15 кг. Витя помог дедушке и донес 2 пакета. Сколько килограммов картофеля нес Витя?
Ответ:
1) 15 : 5 = 3 (кг.) – вес одного пакета. 2) 3 · 2 = 6 (кг.) Ответ: 6 кг картофеля нёс Витя.
Номер 5.
На сколько минут дольше длится игра в футбол, чем в баскетбол, если в игре в футбол 2 тайма по 45 мин, а в игре в баскетбол 4 тайма по 10 мин?
Ответ:
1-й способ решения:
1) 45 ∙ 2 = 90 (мин) – длилась игра в футбол.
2) 4 ∙ 10 = 40 (мин) – длилась игра в баскетбол.
3) 90 – 40 = 50 (мин) – на столько больше минут длилась игра в футбол, чем в баскетбол.
Ответ: на 50 минут больше длилась игра в футбол.
2-й способ решения:
2 ∙ 45 – 4 ∙ 10 = 90 – 40 = 50 (мин) – на сколько больше
Ответ: 50 минут.
Номер 6.
1) Выпиши названия всех треугольников с общей вершиной А. 2) Найди среди этих треугольников равносторонний и подчеркни его название.
1) ABD, ABK, ABC, ADK, ADC, AKC. 2) ABK,.
1) Выпиши названия всех треугольников с общей вершиной А. 2) Найди среди этих треугольников равносторонний и подчеркни его название. 3) Верно ли, что отрезок AD является осью симметрии треугольника ABK?
1) ABD, ABK,, ABC, ADK, ADC, AKC. 2) ABK,. 3) Да, верно
Номер 7.
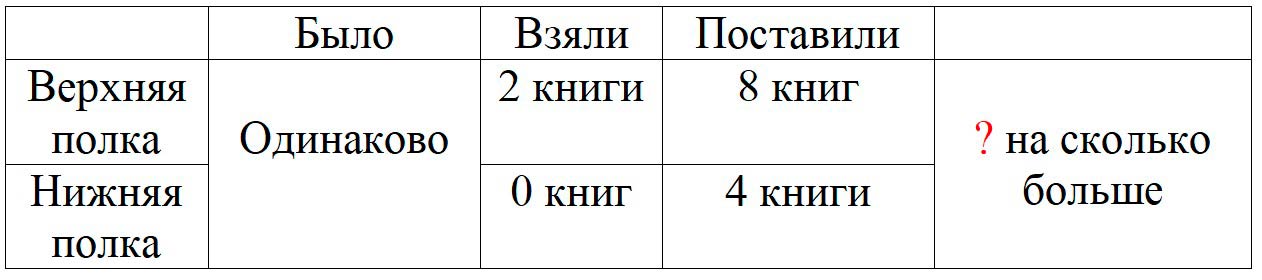
На двух полках книг было поровну. С верхней полки сначала взяли 2 книги, а затем на нее поставили 8 книг, а на нижнюю полку поставили 4 книги. На сколько больше книг стало на верхней полке, чем на нижней?
Ответ:
1) На верхней полке стало на 8 – 2 = 6 книг больше.
2) На нижней полке стало на 4 книги больше.
3) На верхней полке стало на 6 – 4 = 2 книги больше, чем на нижней.
Ответ: на 2 книги больше на верхней полке, чем на нижней.
Задание внизу страницы
Вычисли.
Ответ:92 : 4 = 23 920 : 4 = 230 170 ∙ 5 = 850
Задание на полях страницы
Сравни площади закрашенных фигур:
Площади фигур равны. Первая фигура поделена на 8 частей. Из них закрашены 2 части. Это четвертая часть. Вторая фигура поделена на 16 частей. Из них закрашены 4 части. Это четвертая часть.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.