Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 77

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 6.

1) Во время игры «Поле чудес» Оля набрала 540 очков, Маша − на 120 очков меньше, чем Оля, а Коля − столько очков, сколько Оля и Маша вместе. Сколько очков набрал Коля? 2) Рассмотри таблицу и скажи, какие призы мог выбрать Коля.
Управляемая машина – 110 Шагающая кукла – 120 Электронная игра – 200 Лыжи с палками – 270 Роликовые коньки – 300 Велосипед – 650
Ответ:1)

1) 540 – 120 = 420 очков заработала Маша.
2) 540 + 420 = 960 очков заработал Коля.
2) 110 + 120 + 200 + 270 = 700 (управляемая машина, шагающая кукла, электронная игра, лыжи с палками);
650 + 300 = 950 – (велосипед, роликовые коньки);
650 + 270 = 920 – (велосипед, лыжи с палками);
650 + 200 + 110 = 960 – (велосипед, электронная игра, управляемая машина);
650 + 120 + 110 = 880 – (велосипед, шагающая кукла, управляемая машина).
1) Первое действие вычисляется вычитанием;
2) Второе действием вычисляется сложением.
Оформляем условие в виде краткой записи.
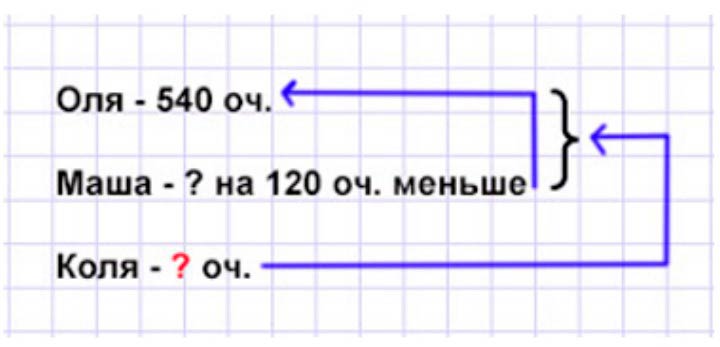
Рассуждаем.
Маша заработала на 120 очков меньше, чем Оля, это столько же но минус 120.
540 − 120 = (500 − 100) + (40 − 20) = 400 + 20 = 420 (оч.) – заработала Маша.
Продолжаем рассуждение.
Коля набрал столько очков сколько Оля и Маша вместе. Значит, чтобы узнать сколько заработал очков коля нужно сложить очки девочек.
540 + 420 = (500 + 400) + (40 + 20) = 900 + 60 = 960 (оч.) – заработал Коля.
Записываем ответ.
Ответ: 960 очков.
Решение выражением:
540 + (540 − 120) = 960 (оч.) – заработал Коля,
где 540 − 120 – очков заработала Маша.
Рассуждаем.
Рассмотрим таблицу.
Соберем призы на сумму равную или меньше 960 очков.
Коля может выбрать:
1)
Управляемая машина, шагающая кукла, электронная гитара и лыжи с палками:
110 + 120 + 200 + 270 = (100 + 100 + 200 + 200) + (10 + 20 + 70) = 600 + 100 = 700 (оч.)
2)
Велосипед, шагающая кукла и управляемая машина:
650 + 120 + 110 = (600 + 100 + 100) + (50 + 20 + 10) = 800 + 80 = 880 (оч.)
3)
Роликовые коньки, лыжи с палками, электронная игра и управляемая кукла:
300 + 270 + 200 + 120 = (300 + 200 + 200 + 100) + (70 + 20) = 800 + 90 = 890 (оч.)
4)
Велосипед и лыжи с палками:
650 + 270 = (600 + 200) + (50 + 70) = 800 + 120 = 920 (оч.)
5)
Велосипед и роликовые коньки:
650 + 300 = (600 + 300) + 50 = 900 + 50 = 950 (оч.)
6)
Велосипед, электронная гитара и управляемая машина:
650 + 200 + 110 = (600 + 200 + 100) + (50 + 10) = 900 + 60 = 960 (оч.)
Оформляем задание в тетрадь.
На 960 очков Коля может выбрать:
1) Управляемая машина, шагающая кукла, электронная гитара и лыжи с палками – 700 оч.
2) Велосипед, шагающая кукла и управляемая машина – 880 оч.
3) Роликовые коньки, лыжи с палками, электронная игра и управляемая кукла – 890 оч.
4) Велосипед и лыжи с палками – 920 оч.
5) Велосипед и роликовые коньки – 950 оч.
6) Велосипед, электронная гитара и управляемая машина – 960 (оч.)
1) Во время игры «Поле чудес» Оля набрала 540 очков, Маша – на 120 очков меньше, чем Оля, а Коля – столько очков, сколько Оля и Маша вместе. Сколько очков набрал Коля? 2) Рассмотри таблицу и скажи, какие призы мог выбрать Коля.
Управляемая машина – 110 Шагающая кукла – 120 Электронная игра – 200 Роликовые коньки – 300 Велосипед – 650
Ответ:1.

1) 540 – 120 = 420 очков заработала Маша.
2) 540 + 420 = 960 очков заработал Коля.
2. 650 + 300 = 950 – (велосипед, роликовые коньки);
650 + 200 + 110 = 960 – (велосипед, электронная игра, управляемая машина);
650 + 120 + 110 = 880 – (велосипед, шагающая кукла, управляемая машина).
300 + 200 + 110 + 120 = 730 – (роликовые коньки, электронную игру, управляемую машину и шагающую куклу).
Повтори как разложить число на разрядные слагаемые.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Маша набрала на 120 очков меньше, чем Оля. Чтобы узнать, сколько очков набрала Маша, нужно из очков, которые набрала Оля, вычесть 120 очков.
540 – 120 = 500 + 40 – 100 – 20 = (500 – 100) + (40 – 20) = 400 + 20 = 420 (оч.) – набрала Маша.
Продолжаем рассуждение.
Коля набрал столько очков, сколько Оля и Маша вместе. Значит, чтобы узнать, сколько набрал очков Коля нужно сложить очки девочек.
540 + 420 = 500 + 40 + 400 + 20 = (500 + 400) + (40 + 20) = 900 + 60 = 960 (оч.) – набрал Коля.
Записываем ответ.
Ответ: 960 очков набрал Коля.
Рассуждаем.
Рассмотрим таблицу.
Соберем призы на сумму равную или меньше 960 очков.
Коля может выбрать:
1) Велосипед и роликовые коньки:
650 + 300 = 600 + 300 + 50 = 900 + 50 = 950 (оч.)
2) Велосипед, электронная игра и управляемая машина:
650 + 200 + 110 = (600 + 200 + 100) + (50 + 10) = 900 + 60 = 960 (оч.)
3) Велосипед, шагающая кукла и управляемая машина:
650 + 120 + 110 = (600 + 100 + 100) + (50 + 20 + 10) = 800 + 80 = 880 (оч.)
4) Роликовые коньки, электронная игра, шагающая кукла и управляемая машина:
300 + 200 + 120 + 110 = (300 + 200 + 100 + 100) + (20 + 10) = 700 + 30 = 730 (оч.)
Оформляем задание в тетрадь.
650 + 300 = 950 – (велосипед, роликовые коньки)
650 + 200 + 110 = 960 – (велосипед, электронная игра, управляемая машина)
650 + 120 + 110 = 880 – (велосипед, шагающая кукла, управляемая машина)
300 + 200 + 110 + 120 = 730 – (роликовые коньки, электронную игру, управляемую машину и шагающую куклу)
Номер 7.
Ответ:
1) Рассмотри алгоритм вычитания трехзначных чисел.
2) Вспомни как складывает и вычитать по разрядам.
3) Помни, что разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Выполняем вычисления с пояснениями.
Выполним вычитание в столбик.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: 6 – 4 = 2
Под единицами пишу 2.
Вычитаю десятки: из 5 дес. нельзя вычесть 8 дес. Беру 1 сот. из 4 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 4.)
1 сот. и 5 дес. — это 15 дес.
15 – 8 = 7
Под десятками пишу 7.
Вычитаю сотни: так как занимали 1 ед. у сотни, то 4 – 1 – 1 = 2
Под сотнями пишу 2.
Читаю ответ: 272.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: из 7 ед. нельзя вычесть 9 ед. Беру 1 дес. из 2 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 2.)
1 дес. и 7 ед. – это 17 ед.
17 – 9 = 8
Под единицами пишу 8.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 2 – 1 – 1 = 0
Разряд десятков отсутствует.
Вычитаю сотни: 5 – 5 = 0
Разряд сотен отсутствует.
Читаю ответ: 8.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: из 1 ед. нельзя вычесть 3 ед. Беру 1 дес. из 3 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 3.)
1 дес. и 1 ед. – это 11 ед.
11 – 3 = 8
Под единицами пишу 8.
Вычитаю десятки: так как занимали 1 ед. у десятков, то 3 – 1 – 0 = 2
Под десятками пишу 2.
Вычитаю сотни: 7 – 4 = 3
Под сотнями пишу 3.
Читаю ответ: 328.
Выполним сложение в столбик.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 4 + 6 = 10
10 ед. – это 1 дес. и 0 ед.; 0 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 6 + 3 + 1 = 10
10 дес. – это 1 сот. 0 дес.; 0 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 1 + 3 + 1 = 5
Пишу под сотнями 5.
Читаю ответ: 500.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 2 + 8 = 10
10 ед. – это 1 дес. и 0 ед.; 0 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 9 + 6 + 1 = 16
16 дес. – это 1 сот. 6 дес.; 6 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 2 + 4 + 1 = 7
Пишу под сотнями 7.
Читаю ответ: 760.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 0 + 6 = 6.
Пишу под единицами 6.
Складываю десятки: 4 + 9 = 13.
13 дес. — это 1 сот. 3 дес.; 3 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 4 + 1 + 1 = 6.
Пишу под сотнями 6.
Читаю ответ: 636.
Выполним вычисления по разрядам:
360 – 60 – 30 = 300 – 30 = (200 + 100) – 30 = 200 + (100 – 30) = 200 + 70 = 270
670 – 10 – 70 = 660 – 70 = (500 + 160) – 70 = 500 + (160 – 70) = 500 + 90 = 590
720 – 200 + 50 = 520 + 50 = (500 + 20) + 50 = 500 + (20 + 50) = 500 + 70 = 570
Оформляем задание в тетрадь.
.jpg)
360 – 60 – 30 = 300 – 30 = 270
670 – 10 – 70 = (670 – 70) – 10 = 600 – 10 = 590
720 – 200 + 50 = 520 + 50 = 570
Номер 8.
Найди сумму, разность, произведение и частное чисел: 24 и 3; 83 и 1; 48 и 2.
Ответ:24 + 3 = 27 83 + 1 = 84 48 + 2 = 50 24 – 3 = 21 83 – 1 = 82 48 – 2 = 46 24 ∙ 3 = 72 83 ∙ 1 = 83 48 ∙ 2 = 96 24 : 3 = 8 83 : 1 = 83 48 : 2 = 24
1) Сумма – это результат сложения;
2) Разность – это результат вычитания;
3) Произведение – это результат умножения;
4) Частное – это результат деления.
Вычисляем.
Рассмотрим числа 24 и 3.
24 + 3 = 27 – сумма
24 − 3 = 21 – разность
24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72 – произведение
24 : 3 = 8 – частное
Продолжаем вычисления.
Рассмотрим числа 83 и 1.
83 + 1 = 84 – сумма
83 − 1 = 82 – разность
83 ∙ 1 = 83 – произведение
83 : 1 = 83 – частное
Если число умножить или разделить на 1, то результат не меняется.
Продолжаем вычисления.
Рассмотрим числа 48 и 2.
48 + 2 = 50 – сумма.
48 − 2 = 46 – разность.
48 ∙ 2 = (40 + 8) ∙ 2 = 80 + 16 = 96 – произведение.
48 : 2 = (40 + 8) : 2 = 20 + 4 = 24 – частное.
Оформляем задание в тетрадь.
24 + 3 = 27
24 − 3 = 21
24 ∙ 3 = 72
24 : 3 = 8
83 + 1 = 84
83 − 1 = 82
83 ∙ 1 = 83
83 : 1 = 83
48 + 2 = 50
48 − 2 = 46
48 ∙ 2 = 96
48 : 2 = 24
Номер 9.

Сравни уравнения каждой пары; сравни их решения.
Ответ:х ∙ 3 = 120
х = 120 : 3
х = 40
Проверка:
40 * 3 = 120
120 = 120
Ответ: х = 40
х : 3 = 120
х = 120 ∙ 3
х = 360
Проверка:
360 : 3 = 120
120 = 120
Ответ: х = 360
х + 90 = 160
х = 160 ‒ 90
х = 70
Проверка:
70 + 90 = 160
160 = 160
Ответ: х = 70
х ‒ 90 = 160
х = 160 + 90
х = 250
Проверка:
250 - 90 = 160
160 = 160
Ответ: х = 250
75 ∙ х = 75
х = 75 : 75
х = 1
Проверка:
75 * 1 = 75
75 = 75
Ответ: х = 1
75 + х = 75
х = 75 ‒ 75
х = 0
Проверка:
75 + 0 = 75
75 = 75
Ответ: х = 0
Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим первый столбик.
х ∙ 3 = 120
х – неизвестный множитель.
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
х = 120 : 3
120 : 3 = (90 + 30) : 3 = 30 + 10 = 40
х = 40
х : 3 = 120
х – неизвестное делимое.
Чтобы найти делимое нужно частное умножить на делитель.
х = 120 ∙ 3
120 ∙ 3 = (100 + 20) ∙ 3 = 300 + 60 = 360
х = 360
Вывод: Уравнения состоят из одинаковых чисел, но неизвестное первого уравнения находится делением, а во втором уравнении – умножением.
Продолжаем рассуждение.
Рассмотрим второй столбик.
х + 90 = 160
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
х = 160 – 90
160 – 90 = 160 - (60 + 30) = (160 – 60) – 30 = 100 = 30 = 70
х = 70
х – 90 = 160
х – неизвестное уменьшаемое.
Чтобы найти уменьшаемое нужно к сумме прибавить вычитаемое.
х = 160 + 90
160 + 90 = (160 + 40) + 50 = 200 + 50 = 250
х = 250
Вывод: Уравнения состоят из одинаковых чисел, но неизвестное первого уравнения находится вычитанием, а во втором уравнении – сложением.
Продолжаем рассуждение.
Рассмотрим третий столбик.
75 ∙ х = 75
х – неизвестный множитель.
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
х = 75 : 75
х = 1
75 + х = 75
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
х = 75 – 75
х = 0
Вывод: Уравнения состоят из одинаковых чисел, но неизвестное первого уравнения находится делением, а во втором уравнении – вычитанием.
Оформляем задание в тетрадь.
.jpg)
.jpg)
.jpg)
Чем похожи и чем различаются уравнения каждой пары и их решения?
Ответ:1 столбик:
Неизвестный множитель находим делением, а неизвестное делимое – умножением.
х ∙ 3 = 120
х = 120 : 3
х = 40
х : 3 = 120
х = 120 ∙ 3
х = 360
2 столбик:
Неизвестное слагаемое находим вычитанием, а неизвестное уменьшаемое – сложением.
х + 90 = 160
х = 160 ‒ 90
х = 70
х ‒ 90 = 160
х = 160 + 90
х = 250
3 столбик:
Неизвестный множитель находим делением, а неизвестное слагаемое – вычитанием.
75 ∙ х = 75
х = 75 : 75
х = 1
75 + х = 75
х = 75 ‒ 75
х = 0
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим 1 столбик.
х ∙ 3 = 120
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 120 : 3
120 : 3 = 12 дес. : 3 = 4 дес. = 40
х = 40
х : 3 = 120
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делитель.
х = 120 ∙ 3
120 ∙ 3 = 12 дес. ∙ 3 = 36 дес. = 360
х = 360
Вывод: Уравнения состоят из одинаковых чисел, но неизвестный множитель в первом уравнении находится делением, а неизвестное делимое во втором уравнении – умножением.
Продолжаем рассуждение.
Рассмотрим 2 столбик.
х + 90 = 160
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
х = 160 – 90
160 – 90 = 160 – (60 + 30) = 160 – 60 – 30 = 100 – 30 = 70
х = 70
х – 90 = 160
х – неизвестное уменьшаемое.
Чтобы найти уменьшаемое, нужно к сумме прибавить вычитаемое.
х = 160 + 90
160 + 90 = 160 + 40 + 50 = 200 + 50 = 250
х = 250
Вывод: Уравнения состоят из одинаковых чисел, но неизвестное слагаемое в первом уравнении находится вычитанием, а неизвестное уменьшаемое во втором уравнении – сложением.
Продолжаем рассуждение.
Рассмотрим 3 столбик.
75 ∙ х = 75
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 75 : 75
х = 1
75 + х = 75
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
х = 75 – 75
х = 0
Вывод: Уравнения состоят из одинаковых чисел, но неизвестный множитель в первом уравнении находится делением, а неизвестное слагаемое во втором уравнении – вычитанием.
Оформляем задание в тетрадь.
х ∙ 3 = 120
х = 120 : 3
х = 40
х : 3 = 120
х = 120 ∙ 3
х = 360
Уравнения состоят из одинаковых чисел, но неизвестный множитель в первом уравнении находится делением, а неизвестное делимое во втором уравнении – умножением.
х + 90 = 160
х = 160 – 90
х = 70
х – 90 = 160
х = 160 + 90
х = 250
Уравнения состоят из одинаковых чисел, но неизвестное слагаемое в первом уравнении находится вычитанием, а неизвестное уменьшаемое во втором уравнении – сложением.
75 ∙ х = 75
х = 75 : 75
х = 1
75 + х = 75
х = 75 – 75
х = 0
Уравнения состоят из одинаковых чисел, но неизвестный множитель в первом уравнении находится делением, а неизвестное слагаемое во втором уравнении – вычитанием.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.