Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 74

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Ответ:
1) Вспомни алгоритм вычитания трехзначных чисел.
2) Вспомни как складывает и вычитать по разрядам.
3) Помни, что разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Рассуждаем и выполняем вычисления.
Выполним письменное сложение.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 8 + 8 = 16
16 ед. – это 1 дес. и 6 ед.; 6 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 4 + 6 + 1 = 11
11 дес. — это 1 сот. 1 дес.; 1 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 3 + 1 + 1 = 5
Пишу под сотнями 5.
Ответ: 516.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 8 + 5 = 13
13 ед. – это 1 дес. и 3 ед.; 3 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 2 + 9 + 1 = 12
12 дес. — это 1 сот. 2 дес.; 2 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 3 + 2 + 1 = 6
Пишу под сотнями 6.
Ответ: 623.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 0 + 0 = 0
Пишу под единицами 0.
Складываю десятки: 4 + 8 = 12
12 дес.— это 1 сот. 2 дес.; 2 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 6 + 1 + 1 = 8
Пишу под сотнями 8.
Ответ: 820.
Выполним письменное вычитание.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: Из 3 ед. нельзя вычесть 9 ед. Беру 1 дес. из 2 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 2.)
1 дес. 3 ед. – это 13 ед.
13 – 9 = 4
Пишу под единицами 4.
Вычитаю десятки: Было 2 дес., но 1дес. взяли при вычитании единиц, поэтому осталось 1 дес.
Из 1 дес. нельзя вычесть 2 дес. Беру 1 сот. из 7 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 7.)
1 сот. 1 дес. – это 11 дес.
11 – 2 = 9
Пишу под десятками 9.
Вычитаю сотни: Было 7 сот., но 1 сот. взяли при вычитании десятков, поэтому осталось 6 сот.
6 – 2 = 4
Пишу под сотнями 4.
Читаю ответ: 494.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы:
5 – 2 = 3
Пишу под единицами 3.
Вычитаю десятки: Из 2 дес. нельзя вычесть 8 дес. Беру 1 сот. из 4 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 4.)
1 сот. 2 дес. – это 12 дес.
12 – 8 = 4
Пишу под десятками 4.
Вычитаю сотни: Было 4 сот., но 1 сот. взяли при вычитании десятков, поэтому осталось 3 сот.
3 – 2 = 1
Пишу под сотнями 1.
Читаю ответ: 143.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: 0 – 0 = 0
Пишу под единицами 0.
Вычитаю десятки: Из 1 дес. нельзя вычесть 9 дес. Беру 1 сот. из 5 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 5.)
1 сот. 1 дес. – это 11 дес.
11 – 9 = 2
Пишу под десятками 2.
Вычитаю сотни: Было 5 сот., но 1 сот. взяли при вычитании десятков, поэтому осталось 4 сот.
4 – 3 = 1
Пишу под сотнями 1.
Читаю ответ: 120.
Вычислим по действиям.
56 : 8 – 1 = 6
1) 56 : 8 = 7
2) 7 – 1 = 6
56 : (8 – 1) = 8
1) 8 – 1 = 7
2) 56 : 7 = 8
Оформляем задание в тетрадь.
.jpg)
56 : 8 – 1 = 7 – 1 = 6
56 : (8 – 1) = 56 : 7 = 8
Номер 2.
1) Сумма двух чисел 648. Одно из чисел 265. Найди разность этих чисел. 2) Разность двух чисел 156. Одно из чисел 127. Найди сумму этих чисел.
Ответ:1) 648 − 265 = 383
383 − 265 = 118
2) 156 + 127 = 283
127 + 283 = 410
1) Сумма – это результат сложения.
2) Разность – это результат вычитания.
Рассуждаем.
Чтобы найти второе слагаемое нужно из суммы вычесть первое слагаемое.
648 − 265 = 383 – второе число.
.jpg)
Второе слагаемое равно 383.
Продолжаем рассуждение.
Чтобы найти разность двух чисел нужно из большего числа вычесть меньшее число.
383 − 265 = 118 – разность чисел.
.jpg)
Значит разность равна 118.
Записываем решение в тетрадь.
1) 648 − 265 = 383 – второе число.
2) 383 − 265 = 118 – разность чисел.
Ответ: 118.
Рассуждаем.
Так как число 127 меньше разности, то 127 – это вычитаемое. Нужно найти уменьшаемое.
Чтобы найти уменьшаемое нужно к разности прибавить вычитаемое.
156 + 127 = 283 – второе число.
.jpg)
Значит уменьшаемое равно 283.
Продолжаем рассуждение.
Чтобы найти сумму двух чисел нужно их значения сложить.
127 + 283 = 410 – сумма чисел.
.jpg)
Значит сумма равна 410.
Записываем решение в тетрадь.
1) 156 + 127 = 283 – второе число.
2) 127 + 283 = 410 – сумма чисел.
Ответ: 410.
Номер 3.
В двух театральных кассах было 705 билетов. Когда из первой кассы продали 267 билетов, в ней осталось 123 билета. Сколько билетов было в каждой кассе сначала?
Ответ:
1) 267 + 123 = 390 (б.) – было в первой кассе. 2) 705 – 390 = 315 (б.) – было во второй кассе. Ответ: 390 билетов было в первой кассе, 315 билетов было во второй кассе.
Вспомни алгоритм складывания и вычитания трехзначных чисел.
Оформляем условие в виде чертежа.
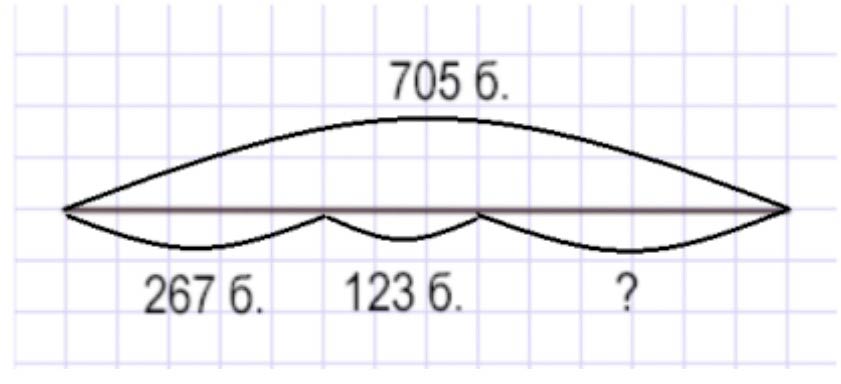
Рассуждаем.
Общее количество билетов в первой кассе складывается из билетов, которые продали и которые осталось продать. Сложим их.
267 + 123 = 390 (б.) – было в первой кассе.
Продолжаем рассуждение.
Общее количество билетов в двух кассах состоит из билетов в первой кассе и во второй кассе.
Чтобы узнать количество билетов во второй кассе нужно из общего количества билетов вычесть количество билетов во второй кассе.
705 – 390 = 315 (б.) – во второй кассе.
Записываем ответ.
Ответ: 390 и 315 билетов.
Номер 4.
На 6 одинаковых пар детских ботинок расходуют 24 дм2 кожи. Сколько квадратных дециметров кожи нужно на 18 пар таких ботинок?
Ответ:
1) 24 : 6 = 4 (дм2) – расход кожи на 1 пару. 2) 18 ∙ 4 = 72 (дм2) – кожи нужно для изготовления 18 пар. Ответ: 72 дм2 кожи всего нужно для изготовления 18 пар таких ботинок.
Данная задача вида «Расход на 1 пару, количество пар, общий расход» характеризуется зависимостями между элементами:
Расход на 1 пару ∙ количество пар = общий расход.
Общий расход : расход на 1 пару = количество пар.
Общий расход : количество пар = расход на 1 пару.
Оформляем условие в виде таблицы.

Рассуждаем.
На 6 пар одинаковых ботинок расходуют 24 дм2 кожи. Одинаковых, т.е. расход на каждую пару ботинок равен.
Чтобы узнать расход на 1 пару, нужно общий расход разделить на количество пар.
24 : 6 = 4 (дм2) – на 1 пару.
Продолжаем рассуждение.
На одну пару ботинок расходуют 4 дм2 кожи. Все пары ботинок одинаковы, значит, чтобы узнать сколько нужно кожи на 18 пар ботинок, умножим количество пар на расход на 1 пару.
18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72 (дм2) – на 18 пар.
Записываем ответ.
Ответ: 72 дм2.
Решение выражением:
18 ∙ (24 : 6) = 72 (дм2) – нужно кожи на 18 пар ботинок, где 24 : 6 – расход кожи на 1 пару ботинок.
Номер 5.
Найди ошибки в вычислениях и запиши правильное решение.
57 : 3 = 19 75 : 25 = 5 80 : 20 = 40 72 : 12 = 6 88 : 8 = 10 98 : 7 = 17 44 : 22 = 2 99 : 9 = 11 96 : 12 = 3
Ответ:57 : 3 = 19 - верно 75 : 25 = 5 - неверно, потому что 75 : 25 = 3 80 : 20 = 40 - неверное, потому что 80 : 2 = 40 72 : 12 = 6 - верно 88 : 8 = 10 - неверно, потому что 88 : 8 = 11 98 : 7 = 17 - неверно, потому что 98 : 7 = 14 44 : 22 = 2 - верно 99 : 9 = 11 - верно 96 : 12 = 3 - неверно, потому что 96 : 12 = 8
1) Помни, чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
2) Вспомни как выполнить деление методом подбора.
Рассуждаем.
Рассмотрим 1 пример.
57 : 3 = (30 + 27) : 3 = 10 + 9 = 19
Представим число 57 как сумму 30 и 27, каждое слагаемое разделим на 3 и полученные результаты сложим.
Сравним результаты: 19 = 19 – вычислено верно.
Рассмотрим 2 пример.
75 : 25 = ?
Пробуем в частном 2 и проверяем: 25 ∙ 2 = 50, 50 < 75, число 2 не подходит.
Пробуем в частном 3 и проверяем: 25 ∙ 3 = 75, 75 = 75, значит 45 : 15 = 3.
Ответ: 3.
Сравним результаты: 3 < 5 – вычисление не верно.
Рассмотрим 3 пример.
80 : 20 = 8 дес. : 2 дес. = 4
Сравним результаты6 4 < 40 – вычисление не верно.
Рассмотрим 4 пример.
72 : 12 = ?
Пробуем в частном 5 и проверяем: 12 ∙ 5 = 60, 60 < 72, число 5 не подходит.
Пробуем в частном 6 и проверяем: 12 ∙ 6 = 72, 72 = 72, значит 72 : 12 = 6.
Ответ: 6.
Сравним результаты: 6 = 6 – вычисление верно.
Рассмотрим 5 пример.
88 : 8 = (80 + 8) : 8 = 10 + 1 = 11
Представим число 88 как сумму 80 и 8, каждое слагаемое разделим на 8 и полученные результаты сложим.
Сравним результаты: 11 > 10 – вычислено не верно.
Рассмотрим 6 пример.
98 : 7 = (70 + 28) : 7 = 10 + 4 = 14
Представим число 98 как сумму 70 и 28, каждое слагаемое разделим на 7 и полученные результаты сложим.
Сравним результаты: 14 < 17 – вычислено не верно.
Рассмотрим 7 пример.
44 : 22 = ?
Пробуем в частном 2 и проверяем: 22 ∙ 2 = 44, 44 = 44, значит 44 : 22 = 2.
Ответ: 2.
Сравним результаты: 2 = 2 – вычисление верно.
Рассмотрим 8 пример.
99 : 9 = (90 + 9) : 9 = 10 + 1 = 11
Представим число 99 как сумму 90 и 9, каждое слагаемое разделим на 9 и полученные результаты сложим.
Сравним результаты: 11 = 11 – вычислено верно.
Рассмотрим 9 пример.
96 : 12 = ?
Пробуем в частном 3 и проверяем: 12 ∙ 3 = 36, 36 < 96, число 3 не подходит.
Пробуем в частном 4 и проверяем: 12 ∙ 4 = 48, 48 < 96, число 4 не подходит.
Пробуем в частном 5 и проверяем: 12 ∙ 5 = 60, 60 < 96, число 5 не подходит.
Пробуем в частном 6 и проверяем: 12 ∙ 6 = 72, 72 < 96, число 6 не подходит.
Пробуем в частном 7 и проверяем: 12 ∙ 7 = 84, 84 < 96, число 7 не подходит.
Пробуем в частном 8 и проверяем: 12 ∙ 8 = 96, 96 = 96, значит 96 : 12 = 8
Ответ: 8.
Сравним результаты: 8 > 3 – вычисление не верно.
Делаем вывод.
57 : 3 = 19 — вычисление выполнено верно.
75 : 25 = 5 — вычисление выполнено неверно, так как 25 ∙ 5 = 125, 125 > 75.
80 : 20 = 40 — вычисление выполнено неверно, так как 20 ∙ 40 = 800, 800 > 80.
72: 12 = вычисление выполнено верно.
88 : 8 = 10 — вычисление выполнено неверно, так как 10 ∙ 8 = 80, 80 < 88.
98 : 7 = 17 — вычисление выполнено неверно, так как 17 ∙ 7 = 119, 119 > 98.
44 : 22 = 2 – вычисление выполнено верно.
99 : 9 = 11 – вычисление выполнено верно.
96 : 12 = 3 — вычисление выполнено неверно, так как 3 ∙ 12 = 36, 36 < 96.
Записываем решение в тетрадь.
Запишем неверные вычисления и исправим ошибки.
75 : 25 = 5 — неправильно.
Верное решение: 75 : 25 = 3.
80 : 20 = 40 — неправильно.
Верное решение: 80 : 20 = 4.
88 : 8 = 10 — неправильно.
Верное решение: 88 : 8 = 11.
98 : 7 = 17 — неправильно.
Верное решение: 98 : 7 = 14.
96 : 12 = 3 — неправильно.
Верное решение: 96 : 12 = 8.
Номер 6.
1) Сумма двух чисел больше одного из них на 12 и больше другого на 18. Найди эту сумму. 2) Вычитаемое меньше уменьшаемого на 32. Найди разность.
Ответ:1) 12 + 18 = 30 2) Разница между вычитаемым и уменьшаемым является разностью. Это значит, что разность в данном случае равна 32, например, 64 - 32 = 32
1) Вспомни названия компонентов действия сложения и вычитанием, а также – зависимость между компонентами и результатами действий сложения и вычитания.
2) Сумма – это результат сложения.
3) Разность – это результат вычитания.
Рассуждаем.
Так как сумма больше одного из чисел на 12, значит другое число и равно 12.
12 – второе число.
Продолжаем рассуждение.
Так как сумму больше другого числа на 18, значит первое число равно 18.
18 – первое число.
Делаем вывод.
Чтобы найти сумму двух числе их значения нужно сложить.
1 число – 18
2 число – 12
18 + 12 = 30 – сумма чисел.
Ответ: 30.
Рассуждаем.
Чтобы найти разность нужно из уменьшаемого вычесть вычитаемое или узнать на сколько вычитаемое меньше уменьшаемого, а это значит, что разность этих чисел и есть число 32.
Записываем ответ.
Ответ: 32.
Задание внизу страницы
Рассмотри рисунок и выпиши номера: 1) разносторонних треугольников; 2) равнобедренных треугольников. Подчеркни номера равносторонних треугольников.

1) Разносторонние треугольники: 3, 5, 2.
2) Равнобедренные треугольники: 1, 6.
Равносторонние треугольники: 7, 4.
Повтори виды треугольников по сторонам: разносторонний, равнобедренный и равносторонний и чем они отличаются.
Рассмотрим треугольники.
С помощью линейки измерим стороны треугольников.
Стороны 1 треугольника – 2 см 2 мм, 2 см 2 мм, 4 см.
Стороны 2 треугольника – 1 см, 3 см 5 мм, 3 см 7 мм.
Стороны 3 треугольника – 1 см 5 мм, 3 см 8 мм, 4 см 5 мм.
Стороны 4 треугольника – 3 см, 3 см, 3 см.
Стороны 5 треугольника – 3 см, 3 см 2 мм, 7 см.
Стороны 6 треугольника – 2 см, 3 см, 3 см.
Стороны 7 треугольника – 2 см, 2 см, 2 см.
Рассуждаем.
1 треугольник – равнобедренный, так как две стороны равны;
2 треугольник – разносторонний, так как все стороны разные;
3 треугольник – разносторонний, так как все стороны разные;
4 треугольник – равносторонний, так как все стороны равны;
5 треугольник – разносторонний, так как все стороны разные;
6 треугольник – равнобедренный, так как две стороны равны;
7 треугольник – равносторонний, так как все стороны равны.
Выполняем задание.
1)
Выпишем номера разносторонних треугольников:
2, 3, 5.
2)
Выпишем номера равнобедренных треугольников:
Равносторонний треугольник также является и равнобедренным.
1, 4, 6, 7.
Подчеркнём номера равносторонних треугольников:
1, 4, 6, 7.
Оформляем задание в тетрадь.
1) 2, 3, 5.
2) 1, 4, 6, 7.
Задание на полях страницы
Лабиринт:

47 + 14 = 61 58 + 3 = 61 35 + 26 = 61 42 + 19 = 61
Подбери такие комбинации чисел, чтобы при сложении получалось 61.
Для этого складывай разные числа, чтобы найти верное решение.
Устные рассуждения.
Нужно сложить два числа, из разных окружностей, чтобы в сумме получить 61.
Записываем решение в тетрадь.
47 + 14 = 61
26 + 35 = 61
3 + 58 = 61
42 + 19 = 61
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.