Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 70

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Приемы письменных вычислений
Номер 1.
Объясни вычисления.


Пишу единицы под единицами, десятки под десятками. Складываю единицы: 4 + 7 = 11 11 ед – это 1 дес. и 1 ед. Пишу 1 ед. под единицами, 1 дес. прибавляю к десяткам. Складываю десятки: 3 + 2 + 1 = 6 6 пишу под десятками. Читаю ответ: 61.

Пишу единицы под единицами, десятки под десятками. Складываю единицы: 4 + 7 = 11 11 ед – это 1 дес. и 1 ед. Пишу 1 ед. под единицами, 1 дес. прибавляю к десяткам. Складываю десятки: 3 + 2 + 1 = 6 6 пишу под десятками. Пишу 5 под сотнями. Читаю ответ: 561.

Пишу единицы под единицами, десятки под десятками. Складываю единицы: 4 + 7 = 11 11 ед – это 1 дес. и 1 ед. Пишу 1 ед. под единицами, 1 дес. прибавляю к десяткам. Складываю десятки: 3 + 2 + 1 = 6 6 пишу под десятками. Складываю сотни: 5 + 4 = 9 Пишу 0 под сотнями. Читаю ответ: 961.

Пишу единицы под единицами, десятки под десятками. Вычитаю единицы: 3 − 7 отнять нельзя. Занимаю десяток: 1 дес. = 10 ед. 13 − 7 = 6 Записываю 6 под единицами. Было 8 десятков и заняли 1, стало 7. Вычитаю десятки: 7 − 6 = 1 Пишу десятки под десятками. Читаю ответ: 16.

Пишу единицы под единицами, десятки под десятками. Вычитаю единицы: 3 − 7 отнять нельзя. Занимаю десяток: 1 дес. = 10 ед. 13 − 7 = 6 Записываю 6 под единицами. Было 8 десятков и заняли 1, стало 7. Вычитаю десятки: 7 − 6 = 1 Пишу под десятками 1. Вычитаю сотни: 4 − 0 = 4 Записываю 4 под сотнями. Читаю ответ: 416.

Пишу единицы под единицами, десятки под десятками. Вычитаю единицы: 3 − 7 отнять нельзя. Занимаю десяток: 1 дес. = 10 ед. 13 − 7 = 6 Записываю 6 под единицами. Было 8 десятков и заняли 1, стало 7. Вычитаю десятки: 7 − 6 = 1 Пишу под десятками 1. Вычитаю сотни: 4 − 1 = 3 Записываю 3 под сотнями. Читаю ответ: 316.
1) Вспомни как складывает и вычитать по разрядам.
2) Помни, что разряд единиц пишем под единицами, десятки под десятками.
Рассуждаем.
Рассмотрим первый пример.
34 + 27 = 61
Разряд единиц пишем под единицами, десятки под десятками.
Складываем поочередно, сначала разряд единиц:
4 + 7 = 11 = 1 дес. и 1 ед.
Пишем 1 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
3 + 2 + 1 = 6
6 пишем в ответе под десятками.
Ответ: 61.
Продолжаем рассуждение.
Рассмотрим второй пример.
534 + 27 = 561
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
4 + 7 = 11 = 1 дес. и 1 ед.
Пишем 1 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
3 + 2 + 1 = 6
6 пишем в ответе под десятками.
5 сотен пишем в ответ в разряд сотен.
Ответ: 561.
Продолжаем рассуждение.
Рассмотрим третий пример.
534 + 427 = 961
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
4 + 7 = 11 = 1 дес. и 1 ед.
Пишем 1 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
3 + 2 + 1 = 6
6 пишем в ответе под десятками.
Складываем сотни: 5 + 4 = 9.
9 пишем в ответе в разряде сотен.
Ответ: 961.
Продолжаем рассуждение.
Рассмотрим четвертый пример.
83 − 67 = 16
Разряд единиц пишем под единицами, десятки под десятками.
Вычитаем поочередно, сначала разряд единиц:
Из 3 отнять 7 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 13 − 7 = 6.
Пишем 6 в ответ в разряде единиц.
Вычитаем десятки: было 8 дес. заняли 1 дес. и вычитаем 6 дес.
8 − 1 − 6 = 1
1 пишем в ответе под десятками.
Ответ: 16.
Продолжаем рассуждение.
Рассмотрим пятый пример.
483 − 67 = 416
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями
Вычитаем поочередно, сначала разряд единиц:
Из 3 отнять 7 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 13 − 7 = 6.
Пишем 6 в ответ в разряде единиц.
Вычитаем десятки: было 8 дес. заняли 1 дес. и вычитаем 6 дес.
8 − 1 − 6 = 1
1 пишем в ответе под десятками.
4 сотен пишем в разряде сотен.
Ответ: 416.
Продолжаем рассуждение.
Рассмотрим шестой пример.
483 − 167 = 316
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 3 отнять 7 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 13 − 7 = 6.
Пишем 6 в ответ в разряде единиц.
Вычитаем десятки: было 8 дес. заняли 1 дес. и вычитаем 6 дес.
8 − 1 − 6 = 1
1 пишем в ответе под десятками.
Вычитаем сотни: 4 − 1 = 3
3 пишем в ответ в разделе сотни.
Ответ: 316.
Номер 2.

Вычисли, используя запись столбиком, и сделай проверку.
Ответ:
1) Вспомни как складывает и вычитать по разрядам.
2) Помни, что разряд единиц пишем под единицами, десятки под десятками.
Выполним вычисления.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
8 + 9 = 17 = 1 дес. и 7 ед.
Пишем 7 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
0 + 2 + 1 = 3
3 пишем в ответе под десятками.
Складываем сотни: 2 + 6 = 8.
8 пишем в ответе в разряде сотен.
Ответ: 837.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 6 отнять 8 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 16 – 8 = 8.
Пишем 8 в ответ в разряде единиц.
Вычитаем десятки: было 5 дес. заняли 1 дес. и осталось 4 дес.
4 – 3 = 1
1 пишем в ответе под десятками.
Вычитаем сотни: 3 – 2 = 1
1 пишем в ответ в разделе сотни.
Ответ: 118.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 6 отнять 7 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 16 – 7 = 9.
Пишем 9 в ответ в разряде единиц.
Вычитаем десятки: было 4 дес. заняли 1 дес. и осталось 3 дес.
3 – 3 = 0
0 пишем в ответе под десятками.
Вычитаем сотни: 4 – 1 = 3
8 пишем в ответ в разделе сотни.
Ответ: 809.
Сделаем проверку.
208 + 629 = 837
Проверка: из суммы вычтем первое слагаемое, получим второе слагаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 7 отнять 9 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 17 – 9 = 8.
Пишем 8 в ответ в разряде единиц.
Вычитаем десятки: было 3 дес. заняли 1 дес. и осталось 2 дес.
2 – 2 = 0
0 пишем в ответе под десятками.
Вычитаем сотни: 8 – 6 = 2
2 пишем в ответ в разделе сотни.
Получилось: 208.
208 = 208 – вычисление выполнено верно.
356 – 238 = 118
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
8 + 8 = 16 = 1 дес. и 6 ед.
Пишем 6 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
1 + 3 + 1 = 5
5 пишем в ответе под десятками.
Складываем сотни:
1 + 2 = 3
3 сотен пишем в ответ в разряд сотен.
Получилось: 356.
356 = 356 – вычисление выполнено верно.
846 – 37 = 809
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
9 + 7 = 16 = 1 дес. и 6 ед.
Пишем 6 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
0 + 3 + 1 = 4
4 пишем в ответе под десятками.
8 пишем в ответе в разряде сотен.
Получилось: 846.
846 = 846 – вычисление выполнено верно.
Оформляем задание в тетрадь.
.jpg)
Вычисли и выполни проверку. 208 + 629 356 - 238 846 – 37
Ответ:
1) Вспомни, как складывать и вычитать по разрядам.
2) Помни, что разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Выполним вычисления.
-(2024).jpg)
Складываем поочередно, сначала разряд единиц:
8 + 9 = 17 = 1 дес. и 7 ед.
Пишем 7 в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки:
0 + 2 + 1 = 3
Пишем 3 в ответе под десятками.
Складываем сотни:
2 + 6 = 8.
Пишем 8 в ответе под сотнями.
Ответ: 837.
-(2024).jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 6 отнять 8 нельзя, поэтому занимает 1 единицу у десяток, 1 дес. = 10 ед., получаем 6 + 10 = 16, теперь можем вычесть 16 – 8 = 8.
Пишем 8 в ответ под единицами.
Вычитаем десятки:
было 5 дес., заняли 1 дес.: 5 – 1 = 4 дес. осталось 4 – 3 = 1
Пишем 1 в ответе под десятками.
Вычитаем сотни:
3 – 2 = 1
Пишем 1 в ответ под сотнями.
Ответ: 118.
-(2024).jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 6 отнять 7 нельзя, поэтому занимает 1 единицу у десяток, 1 дес. = 10 ед., получаем 6 + 10 = 16, теперь можем вычесть 16 – 7 = 9
Пишем 9 в ответ под единицами.
Вычитаем десятки:
было 4 дес., заняли 1 дес.: 4 – 1 = 3 дес. осталось 3 – 3 = 0
Пишем 0 в ответе под десятками.
В первом числе есть 8 сот., а второе число двузначное, в нём нет сотен, поэтому цифру 8 просто переносим в ответ под сотнями.
Ответ: 809.
Сделаем проверку.
208 + 629 = 837
Проверка: из суммы вычтем второе слагаемое, получим первое слагаемое.
-(2024).jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 7 отнять 9 нельзя, поэтому занимает 1 единицу у десяток, 1 дес. = 10 ед., получаем 7 + 10 = 17, теперь можем вычесть 17 – 9 = 8
Пишем 8 в ответ под единицами.
Вычитаем десятки:
было 3 дес., заняли 1 дес.: 3 – 1 = 2 дес. осталось 2 – 2 = 0
Пишем 0 в ответе под десятками.
Вычитаем сотни:
8 – 6 = 2
Пишем 8 в ответ в под сотнями.
Получилось: 208.
208 = 208 – вычисление выполнено верно.
356 – 238 = 118
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
-(2024).jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
8 + 8 = 16 = 1 дес. и 6 ед.
Пишем 6 в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки:
1 + 3 + 1 = 5
Пишем 5 в ответе под десятками.
Складываем сотни:
1 + 2 = 3.
Пишем 3 в ответе под сотнями.
Получилось: 356.
356 = 356 – вычисление выполнено верно.
846 – 37 = 809
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
-(2024).jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
9 + 7 = 16 = 1 дес. и 6 ед.
Пишем 6 в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки:
0 + 3 + 1 = 4
Пишем 4 в ответе под десятками.
В первом числе есть 8 сот., а второе число двузначное, в нём нет сотен, поэтому цифру 8 просто переносим в ответ под сотнями.
Получилось: 846.
846 = 846 – вычисление выполнено верно.
Оформляем задание в тетрадь.
-(2024).jpg)
Номер 3.
В городе 156 школ, а детских садов на 30 меньше. Сколько всего ...?
Ответ:В городе 156 школ, а детских садов на 30 меньше. Сколько всего в городе школ и детских садов вместе?

1) 156 – 30 = 126 (д.с.) – в городе 2) 156 + 126 = 282 (уч.) – в городе школ и детских садов. Ответ: в городе всего 282 школы и детских сада.
1) «На 30 меньше» – вычисляется вычитанием.
2) Вопрос: Сколько всего в городе школ и детских садов вместе?
Оформляем условие в виде краткой записи.
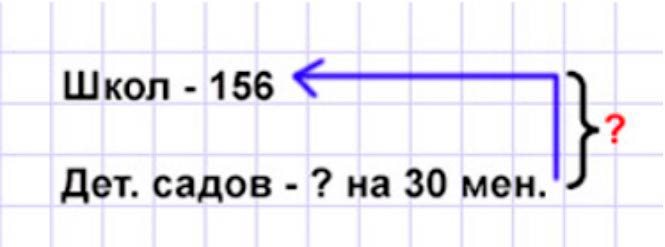
Рассуждаем.
Детских садов на 30 меньше, чем школ, значит из количества школ нужно вычесть 30 зданий.
156 − 30 = 100 + (56 − 30) = 126 (зд.) – детских садов.
Продолжаем рассуждение.
Общее количество зданий складывается из школ и детских садов. Сложим эти значения.
126 + 156 = (100 + 100) + (26 + 56) = 200 + 82 = 282 (зд.) – всего.
Записываем ответ.
Ответ: 282 здания.
Решение выражением:
156 + (156 – 30) = 282 (зд.) – всего,
где 156 – 30 – детских садов.
Номер 4.
Зимой в городе было 36 открытых катков, а катков с искусственным льдом в 9 раз меньше. На сколько больше ...?
Ответ:Зимой было 36 открытых катков, а катков с искусственным льдом в 9 раз меньше. На сколько больше открытых катков, чем искусственных?

1) 36 : 9 = 4 (к.) – с искусственным льдом. 2) 36 – 4 = 32 (к.) Ответ: на 32 катка больше открытых, чем искусственных.
1) «В 9 раз меньше» – вычисляется делением.
2) «На сколько больше» – вычисляется вычитанием.
3) Вопрос: На сколько больше открытых катков, чем катков с искусственным снегом?
Оформляем условие в виде краткой записи.
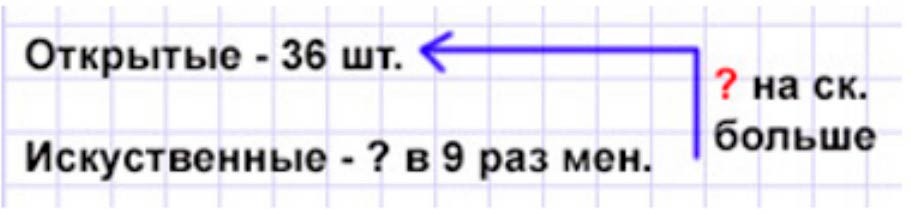
Рассуждаем.
Катков с искусственным льдом в 9 раз меньше, чем открытых катков, значит количество открытых катков нужно разделить на 9.
36 : 9 = 4 (кат.) – с искусственным снегом.
Продолжаем рассуждение.
Чтобы узнать на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
36 − 4 = 32 (кат.) – на сколько больше открытых катков, чем с искусственном льдом.
Записываем ответ.
Ответ: на 32 катка.
Решение выражением:
36 – 36 : 9 = 32 (кат.) – на сколько больше,
где 36 : 9 – количество катков с искусственном снегом.
Номер 5.
Ответ:44 : 2 ∙ 4 = 22 * 4 = 88
88 : 44 ∙ 36 = 2 * 36 = 72
13 ∙ 7 – 8 ∙ 5 = 91 - 40 = 51
18 ∙ 4 + 6 ∙ 4 = 72 + 24 = 96
200 − (36 + 14) = 200 - 50 = 150
700 − (83 + 17) = 700 - 100 = 600
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1 2
44 : 2 · 4 = 88
1) 44 : 2 = (40 + 4) : 2 = 20 + 2 = 22
2) 22 ∙ 4 = (20 + 2) ∙ 4 = 80 + 8 = 88
1 2
88 : 4 ∙ 36 = 72
1) 88 : 44 = 2
2) 2 ∙ 36 = 2 ∙ (30 + 6) = 60 + 12 = 72
1 3 2
13 ∙ 7 − 8 ∙ 5 = 51
1) 13 ∙ 7 = (10 + 3) ∙ 7 = 70 + 21 = 91
2) 8 ∙ 5 = 40
2) 91 − 40 = 51
1 3 2
18 ∙ 4 + 6 ∙ 4 = 96
1) 18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72
2) 6 ∙ 4 = 24
3) 72 + 24 = 96
2 1
200 − (36 + 14) = 150
1) 36 + 14 = 50
2) 200 − 50 = 150
2 1
700 − (83 + 17) = 600
1) 83 + 17 = 100
2) 700 − 100 = 600
Оформляем задание в тетрадь.
1 2
44 : 2 · 4 = 22 · 4 = 88
1 2
88 : 4 ∙ 36 = 2 · 36 = 72
1 3 2
13 ∙ 7 − 8 ∙ 5 = 91 − 40 = 51
1 3 2
18 ∙ 4 + 6 ∙ 4 = 72 + 24 = 96
2 1
200 − (36 + 14) = 200 − 50 = 150
2 1
700 − (83 + 17) = 700 − 100 = 600
Номер 6.
1) Площадь одной двенадцатой части квадрата 3 см2. Найди площадь всего квадрата. 2) Начерти квадрат, площадь которого равна площади прямоугольника со сторонами 2 см и 8 см. Найди периметр этого квадрата.
Ответ:Задача 1:
3 ∙ 12 = 36 (см2) – площадь всего квадрата.
Ответ: площадь всего квадрата составляет 36 см2.
Задача 2:
1) 2 ∙ 8 = 16 (см2) – площадь квадрата и прямоугольника.
2) 16 : 4 = 4 (см) – длина стороны квадрата.
3) Р = 4 ∙ 4 = 16 (см) – периметр квадрата.
Ответ: периметр квадрата 16 см.

1) Площадь – часть плоскости, которую занимает фигура.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Общая площадь квадрата неизвестна, но знаем, что её двенадцатая часть равна 3 см2.
Общая площадь квадрата складывается из площади каждой из 12 частей. Значит, чтобы узнать, чему равна площадь всего квадрата, нужно сложить площадь каждой из частей.
Но площадь каждой части одинаковая, поэтому сложение одинаковых слагаемых можно заменить умножением. И площадь одной части нужно умножить на количество этих частей.
Продолжаем рассуждение.
3 см2 ∙ 12 = 36 см2 – площадь квадрата.
Записываем ответ.
Ответ: 36 см2.
Рассуждаем.
Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2 см ∙ 8 см = 16 см2 – площадь прямоугольника
Продолжаем рассуждение.
Площадь квадрата равна площади прямоугольника, значит площадь квадрата равна 16 см2.
Чтобы найти площадь квадрата нужно длину умножить на ширину. Но у квадрата все стороны равны.
Значит нужно подобрать такое число, чтобы произведение его само на себя было равно 16. Это число 4, так как 4 ∙ 4 = 16.
4 см – длина квадрата.
Продолжаем рассуждение.
Чтобы найти периметр квадрата нужно длину стороны квадрата умножить на количество сторон квадрата, а у квадрата 4 стороны. В итоге, нужно сторону квадрата умножить на 4.
4 см ∙ 4 = 16 см – периметр квадрата.
Начертим.
Начертим квадрат со стороной 4 см.
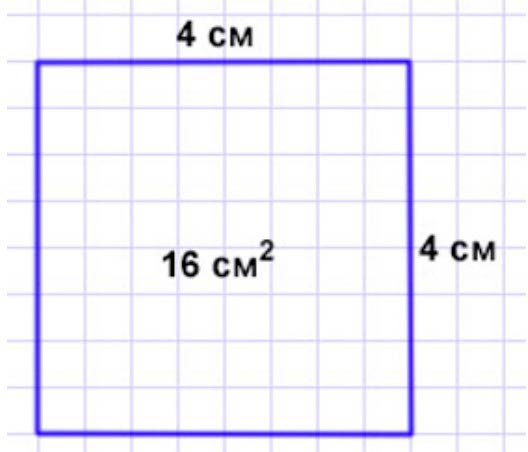
Ответ: 4 см, 16 см.
Номер 7.
Ответ:1 дм − 1 см = 10 см − 1 см = 9 см 1 дм2 − 1 см2 = 99 см2
1) Помни, что 1 дм = 10 см;
2) Помни, что 1 дм2 = 100 см2.
Выполняем вычисления с пояснениями.
1 дм – 1 см = 10 см – 1 см = 9 см, так как 1 дм = 10 см.
1 дм2 – 1см см2 = 100 см2 – 1 см2 = 99 см2, так как 1 дм2 = 100 см2
Оформляем задание в тетрадь.
1 дм – 1 см = 9 см
1 дм2 – 1 см2 = 99
Номер 8.

Юре 10 лет. Мама старше Юры на 26 лет, папа старше мамы на 7 лет. На сколько лет папа старше Юры? Реши задачу одним действием.
Ответ:
26 + 7 = 33 (г.) – на столько старше. Ответ: папа старше Юры на 33 года.
«Старше на ... » – выполняется сложением.
Оформляем условие в виде краткой записи или чертежа.
Краткая запись:
.jpg)
Чертеж:
.jpg)
Рассуждаем.
Возраст мамы больше возраста Юры на 26 лет, а возраст папы больше возраста мамы на 7 лет.
По чертежу видно, что разница возрастов между Юрой и папой складывается из разницы возраста Юры и мамы и разницы возраста мамы и папы.
26 + 7 = 33 (г) – на сколько папа старше Юры.
Записываем ответ.
Ответ: на 33 года.
Юре 10 лет. Мама старше Юры на 26 лет, папа старше мамы на 7 лет. Можно ли решить задачу одним действием? Если да, покажи как. Какое данное в условии задачи при этом станет лишним?
Ответ:Чтобы ответить на вопрос, нужно сложить разницу в возрастах (между Юрой и мамой и мамой и папой). Лишнее в условии задачи – это возраст Юры.

26 + 7 = 33 (г.) – на столько старше. Ответ: папа старше Юры на 33 года.
«Старше на …», значит на сколько-то больше – выполняется сложением.
Оформляем условие в виде схематичного рисунка.
.jpg)
Рассуждаем.
Возраст мамы больше возраста Юры на 26 лет, а возраст папы больше возраста мамы на 7 лет.
Если нужно узнать, на сколько папа старше Юры, то возраст Юры будет лишней информацией, и задачу можно будет решить одним действием.
По рисунку видно, что разница в возрасте между Юрой и папой складывается из разницы возраста Юры и мамы и разницы возраста мамы и папы.
26 + 7 = 33 (г) – на столько папа старше Юры.
Записываем ответ
Ответ: на 33 года папа старше Юры.
Номер 9.
Какое число пропущено?
Ответ:1, 3, 9, 27, 81. После 1, каждое следующее число больше предыдущего в 3 раза.
1) Прежде, чем дополнить ряд чисел, необходимо выявить закономерность, т.е. правило, как он составлен.
2) Для этого рассмотри числа с разных сторон: сколько в нем знаков, на что они делятся, из каких цифр составлены.
Рассуждаем.
Каждое последующее число больше предыдущего в 3 раза, так как:
1 ∙ 3 = 3
3 ∙ 3 = 9
9 ∙ 3 = 27 – пропущенное число.
27 ∙ 3 = 81
Оформляем задание в тетрадь.
1, 3, 9, 27, 81.
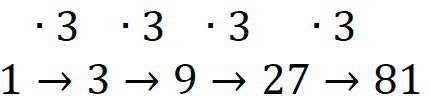
Задание внизу страницы
Вычисли.
Ответ:
1) Вспомни как складывает и вычитать по разрядам.
2) Помни, что разряд единиц пишем под единицами, десятки под десятками.
Выполняем вычисления с пояснениями.
Выполним вычисления в столбик.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
8 + 6 = 14 = 1 дес. и 4 ед.
Пишем 4 ед. в ответе под единицами, а вторая 1 пойдет в разряд десяток.
Складываем десятки:
2 + 4 + 1 = 7
7 пишем в ответе под десятками.
Складываем сотни:
3 + 2 = 5
5 сотен пишем в ответ в разряд сотен.
Ответ: 574.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 4 отнять 9 нельзя поэтому занимает 1 единицу у десяток, то есть 10, получаем: 14 – 9 = 5.
Пишем 5 в ответ в разряде единиц.
Вычитаем десятки: было 7 дес. заняли 1 дес. и осталось 6 дес.
6 – 3 = 3
3 пишем в ответе под десятками.
Вычитаем сотни: 5 – 1 = 4
4 пишем в ответ в разделе сотни.
Ответ: 435.
Оформляем задание в тетрадь.
.jpg)
328 + 246 = (300 + 200) + (20 + 40) + (8 + 6) = 500 + 60 + 14 = 574
574 – 139 = (574 – 100) – 39 = (474 – 30) – 9 = 434 – 9 = 435
Задание на полях страницы
Ребусы:


Вспомни названия компонентов действия сложения и вычитания, а также – зависимость между компонентами и результатами действий сложения и вычитания.
Рассмотрим ребус 1.
Рассуждаем.
Количество единиц первого слагаемого неизвестно, но узнать количесвто единиц можно, если из единиц суммы вычесть единицы второго слагаемого.
9 ед. – 6 ед. = 3 ед.
В первом слагаемом 3 единицы.
Продолжаем рассуждение.
Количетво десяток второго слагаемого неизвестно. Но чтобы узнать количество десяток второго слагаемого, нужно из десяток значения суммы вычесть количество десяток первого слагаемого.
Из 2 дес. мы не можем вычесть 5 дес., значит занимаем 1 сот. = 10 дес.,
10 + 2 = 12 дес.
12 дес. – 5 дес. = 7 дес.
Значит, во втором слагаемом 7 десятков.
Продолжаем рассуждение.
Так как при сложении десятков один разряд ушел в сотни, то:
3 сот. – 1 сот. = 2 сот.
Значит, в первом слагаемом 2 сотни.
Оформляем задание в тетрадь.
.jpg)
Рассуждаем.
Количество единиц вычитаемого неизвестно. Но количество единиц вычитаемого можно узнать, если из количества единиц уменьшаемого вычесть количество единиц значения разности.
Из 6 ед. нельзя вычесть 8 ед., значит занимает 1 дес. = 10 ед.,
10 + 6 = 16 ед.
16 ед. – 8 ед. = 8 ед.
Значит, в вычитаемом 8 единиц.
Продолжаем рассуждение.
Количсетво десятков уменьшаемого неизвестно. Но количсевто десятков уменьшаемого можно узнать, если сложить количество десятков вычитаемого и разности.
7 дес. + 1 дес. = 8 дес. и ещё 1 дес., который занимали при нахождении единиц, 8 дес. + 1 дес. = 9 дес.
Значит, в уменьшаемом 9 десятков.
Продолжаем рассуждение.
Так как в разделе нет разряда сотен, значит значение сотен у уменьшаемого и вычитаемого равны.
В уменьшаемом 2 сотни.
Оформляем задание в тетрадь.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.