Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 69

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Объясни разные способы вычислений и закончи решение.
Ответ:260 + 310 = (260 + 300) + 10 = 570 260 + 310 = (200 + 300) + (60 + 10) = 570 670 − 140 = (670 − 100) − 40 = 530 670 − 140 = (600 − 100) + (70 − 40) = 530
1) Вспомни как образуются и называются трёхзначные числа.
2) Повтори как разложить число на разрядные слагаемые.
Рассуждаем.
Рассмотрим первый пример.
1 способ: 260 + 310 = (260 + 300) + 10 = 560 + 10
Число 310 разложим на сумму 300 и 10. К числу 260 вначале прибавим 300, а потом число 10.
2 способ: 260 + 310 = (200 + 300) + (60 + 10) = 500 + 70
Число 260 и 310 разложим на сумму разрядных слагаемых, потом отдельно сложим сотни и десятки.
Рассмотрим второй пример.
1 способ: 670 – 140 = (670 – 100) – 40 = 570 – 40 = 530
Число 140 разложим на сумму 100 и 40. Из числа 670 вначале вычтем 100, а потом число 40.
2 способ: 670 – 140 = (600 - 100) + (70 – 40) = 500 + 30 = 530
Число 670 и 140 разложим на сумму разрядных слагаемых, потом по-отдельности из сотен первого числа вычтем сотни второго числа, а из десяток первого числа – десятки второго числа, после полученные результаты сложим.
Делаем вывод и вычисляем.
В первом способе вычисления второе число раскладывают на разряды: на сотни и десятки, потом к первому числу отдельно прибавляют сотни, а после десятки. (из первого числа вычитают сотни, а после вычитают десятки)
Во втором способе вычисления два числа раскладывают по разрядам: на стони и десятки, потом по отдельности складывают (вычитают) разряды сотен и разряды десяток, после полученные данные, складывают.
260 + 310 = (260 + 300) + 10 = 560 + 10 = 570
260 + 310 = (200 + 300) + (60 + 10) = 500 + 70 = 570
670 − 140 = (670 − 100) − 40 = 570 − 40 = 530
670 − 140 = (600 − 100) + (70 − 40) = 500 + 30 = 530
Номер 1.
Вычисли с устным объяснением.
Ответ:570 + 240 = (570 + 30) + 210 = 600 + 210 = 810
Если представить число 240 в виде суммы чисел 30 и 210, то затем легко прибавить 30 к 570, а к их сумме 210.
360 + 170 = (360 + 40) + 130 = 400 + 130 = 530
Если представить число 170 в виде суммы чисел 40 и 130, то затем легко прибавить 40 к 360, а к их сумме 130.
760 – 480 = (760 − 460) – 20 = 300 – 20 = 280
Если представить число 480 в виде суммы чисел 60 и 420, то затем легко отнять от 760 60, а затем еще 420.
540 + 290 = (540 + 60) + 230 = 600 + 230 = 830
Если представить число 290 в виде суммы чисел 60 и 230, то затем легко прибавить 60 к 540, а к их сумме 230.
320 – 160 = (320 − 120) – 40 = 200 – 40 = 160
Если представить число 160 в виде суммы чисел 20 и 140, то затем легко отнять от 320 20, а затем еще 140.
430 + 180 = (430 + 20) + 160 = 450 + 160 = 610
Если представить число 180 в виде суммы чисел 70 и 110, то затем легко прибавить 70 к 430, а к их сумме 110.
1) Вспомни как образуются и называются трёхзначные числа.
2) Повтори как разложить число на разрядные слагаемые.
Выполняем вычисления с пояснениями.
570 + 240 = (570 + 200) + 40 = 770 + 40 = 810
1) Число 240 представим в виде разрядных слагаемых: 200 + 40.
2) К числу 570 сначала прибавим 200, а потом число 40 и получим 810.
360 + 170 = (360 +100) + 70 = 460 + 70 = 530
1) Число 170 представим в виде разрядных слагаемых: 100 + 70.
2) К числу 360 сначала прибавим 100, а потом число 70 и получим 530.
760 – 480 = (760 – 460) – 20 = 300 – 20 = 280
1) Число 480 разложим на сумму 460 и 20.
2) Из числа 760 сначала вычтем 460, а потом 20 и получим 280.
540 + 290 = (540 + 200) + 90 = 740 + 90 = 830
1) Число 290 представим в виде разрядных слагаемых: 200 + 90.
2) К числу 540 сначала прибавим 200, а потом число 90 и получим 830.
320 – 160 = (320 – 120) – 40 = 200 – 40 = 160
1) Число 160 разложим на сумму 120 и 40.
2) Из числа 320 сначала вычтем 120, а потом 40 и получим 160.
430 + 180 = (430 + 100) + 80 = 530 + 80 = 610
1) Число 180 представим в виде разрядных слагаемых: 100 + 80.
2) К числу 430 сначала прибавим 100, а потом число 80 и получим 610.
Оформляем задание в тетрадь.
570 + 240 = (500 + 200) + (70 + 40) = 700 + 110 = (700 + 100) + 10 = 810
360 + 170 = (300 + 100) + (60 + 70) = 400 + 130 = (400 + 100) + 30 = 530
760 − 480 = (600 − 400) + (160 − 80) = 200 + 80 = 280
540 + 290 = (500 + 200) + (40 + 90) = 700 + 130 = (700 + 100) + 30 = 830
320 − 160 = (200 − 100) + (120 − 60) = 100 + 60 = 160
430 + 180 = (400 + 100) + (30 + 80) = 500 + 110 = (500 + 100) + 10 = 610
Номер 2.
Дополни 600 г до 1 кг; 420 г до 500 г; 280 г до 300 г; 540 г до 600 г.
Ответ:600 г + 400 г = 1000 г = 1 кг 420 г + 80 г = 500 г 280 г + 20 г = 300 г 540 г + 60 г = 600 г
1) Помни, что 1 кг = 1000 г.
2) Чтобы дополнить число до нужного числа, нужно узнать разницу между этими числами.
3) Повтори, как складывать и вычитать трёхзначные числа.
Рассуждаем.
Чтобы узнать разницу между числами, нужно из большего числа вычесть меньшее.
1)
400 – 340 = 40 дес. – 34 дес. = 6 дес. = 60
Числу 340 до 400 не хватает 60.
1)
1 кг = 1000 г
1000 г – 600 г = 400 г
600 г до 1 кг не хватает 400 г
600 г + 400 г = 1000 г = 1 кг
2)
500 г – 420 г = 80 г
420 г до 500 г не хватает 80 г
420 г + 80 г = 500 г
3)
300 г – 280 г = 20 г
280 г до 300 г не хватает 20 г
280 г + 20 г = 300 г
3)
600 г – 540 г = 60 г
540 г до 600 г не хватает 60 г
540 г + 60 г = 600 г
Оформляем задание в тетрадь.
1) 600 г + 400 г = 1000 г = 1 кг
2) 420 г + 80 г = 500 г
3) 280 г + 20 г = 300 г
4) 540 г + 60 г = 600 г
Номер 3.
За неделю краеведческий музей посетили три первых класса, по 24 человека в каждом, и два вторых класса, по 28 человек в каждом. На сколько больше было на этой неделе в музее первоклассников, чем второклассников?
Ответ:
1) 24 ∙ 3 = 72 (ч.) – первоклассника посетило краеведческий музей. 2) 28 ∙ 2 = 56 (ч.) – второклассника посетило краеведческий музей. 3) 72 – 56 = 16 (ч.) – на столько больше первоклассников посетило музей, чем второклассников. Ответ: на 16 человек больше было в музее первоклассников, чем второклассников.
«На сколько больше» – вычисляется вычитанием.
Оформляем условие в виде краткой записи или таблицы.
Каткая запись:
.jpg)
Таблица:
.jpg)
Рассуждаем.
Общее количество первоклассников складывается из количества детей в каждом классе, но количество детей в каждой классе одинаково, поэтому сумму одинаковых слагаемых можно заменить умножением.
24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72 (ч.) – всего первоклассников.
Продолжаем рассуждение.
Общее количество второклассников складывается из количества детей в каждом классе, но количество детей в каждой классе одинаково, поэтому сумму одинаковых слагаемых можно заменить умножением.
28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56 (ч.) – всего второклассников.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
72 − 56 = 72 − (52 + 4) = (72 − 52) − 4 = 20 − 4 = 16 (ч.) – на столько больше первоклассников, чем второклассников.
Записываем ответ.
Ответ: на 16 человек.
Решение выражением:
24 ∙ 3 – 28 ∙ 2 = 16 (ч.) – на сколько больше,
где 24 ∙ 3 – количество первоклассников;
28 ∙ 2 – количество второклассников.
Номер 4.
Школа, магазин и аптека расположены на одной стороне улицы. От школы до магазина 700 м, от магазина до аптеки на 400 м меньше. Какое расстояние от школы до аптеки? Сделай по условию разные чертежи и реши задачи.
Ответ:Задача 1:

700 + (700 − 400) = 1000 (м)
Ответ: общее расстояние от школы до аптеки составляет 1000 м.
Задача 2:

700 − (700 − 400) = 400 (м) Ответ: общее расстояние от школы до аптеки составляет 400 м.
1) Внимательно прочитай задачу и рассмотри разные варианты как расположены школа, магазин и аптека.
2) «На 400 м меньше» – вычисляется вычитанием.
Оформляем условие в виде чертежа.
Рассмотрим вариант, когда магазин находится между школой и аптекой.
.jpg)
Рассуждаем.
Расстояние от магазина до аптеки на 400 м меньше, чем от школы до магазина.
На 400 м меньше, это столько же, но минус 400 м.
700 − 400 = 300 (м) – расстояние от магазина до аптеки.
Продолжаем рассуждение.
Общее расстояние от школы до аптеки складывается из расстояний от школы до магазина и от магазина до аптеки. Сложим эти расстояния.
700 + 300 = 7 сот. + 3 сот. = 10 сот. = 1000 (м) = 1 км – расстояние от школы до аптеки.
Записываем ответ.
Ответ: 1 км.
Решение выражением:
700 = (700 − 400) = 1000 (м) = 1 (км) – расстояние от школы до аптеки,
где 700 − 400 – расстояние от магазина до аптеки.
Оформляем условие в виде чертежа.
Рассмотрим вариант, когда аптека находится между школой и магазином.
.jpg)
Рассуждаем.
Расстояние от магазина до аптеки на 400 м меньше, чем от школы до магазина.
На 400 м меньше, это столько же, но минус 400 м.
700 − 400 = 300 (м) – расстояние от аптеки до магазина.
Продолжаем рассуждение.
Расстояние от школы до магазина складывается из расстояний от школы до аптеки и аптеки до магазина.
Значит, чтобы найти расстояние от школы до аптеки, нужно из расстояния от школы до магазина вычесть расстояние от аптеки до магазина.
700 − 300 = 400 (м) – расстояние от школы до аптеки.
Записываем ответ.
Ответ: 400 м.
Решение выражением:
700 − (700 − 400) = 400 (м) – расстояние от школы до аптеки,
где 700 − 400 – расстояние от аптеки до магазина.
Номер 5.
Составь по таблице задачу и реши ее.

Первая бригада изготавливает 30 деталей в час, а вторая 40 деталей в час. Сколько деталей изготовят обе бригады вместе за 3 часа?
1-й способ решения:
1) 30 ∙ 3 = 90 (д.) – изготовит первая бригада за 3 часа.
2) 40 ∙ 3 = 120 (д.) – изготовит вторая бригада за 3 часа.
3) 120 + 90 = 210 (д.) – всего изготовят бригады за 3 часа.
2-й способ решения:
1) 30 + 40 = 70 (д.) – в час изготавливают обе бригады.
2) 70 · 3 = 210 (д.) – всего изготовят бригады за 3 часа.
Выражением:
(30 + 40) · 3 = 210
Ответ: 210 деталей за 3 часа изготовят обе бригады, работая вместе.
Данная задача: вида «изготавливали в час, время работы, всего изготовили» характеризуется зависимостями между элементами:
Изготавливали в час · время работы = всего изготовили.
Всего изготовили: изготавливали в час = время работы.
Всего изготовили: время работы = изготавливали в час.
Составляем задачу по таблице.
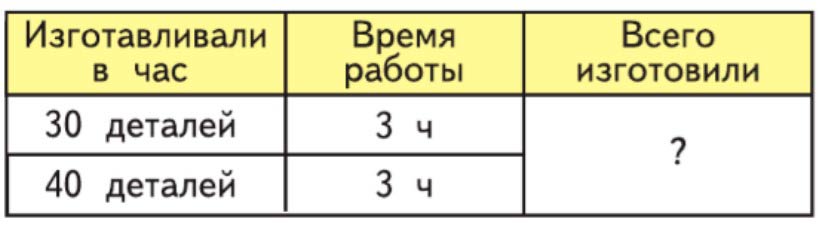
Первая и вторая бригады работали 3 часа. Первая бригада изготавливала 30 деталей в час, а вторая – 40 деталей в час. Сколько всего деталей изготовили две бригады совместно?
Рассуждаем.
Производительность деталей двух бригад за час складывается из деталей каждой бригады, которую они изготавливают за 1 час.
30 + 40 = 70 (дет.) – изготовили обе бригады за 1 час.
Продолжаем рассуждение.
Каждый час бригады изготавливали одинаковое число деталей. Поэтому чтобы узнать сколько изготовили деталей обе бригады за 3 часа, нужно производительность деталей двух бригад за 1 час умножить на количества часов.
70 ∙ 3 = 7 дес. ∙ 3 = 21 дес. = 210 (дет.) – изготовили обе команды за 3 часа.
Записываем ответ.
Ответ: 210 деталей.
Решение выражением:
(30 + 40) ∙ 3 = 210 (дет.) – изготовили всего,
где 30 + 40 – производительность деталей двух команд за 1 час.
Рассуждаем.
Первая бригада каждый час изготавливала одинаковое количество деталей, поэтому чтобы узнать сколько она изготовила за 3 часа нужно количество деталей, изготовленных за час, умножить на количество часов.
30 ∙ 3 = 3 ∙ 3 дес. = 9 дес. = 90 (дет.) – изготовила первая бригада за 3 часа.
Продолжаем рассуждение.
Вторая бригада каждый час изготавливала одинаковое количество деталей, поэтому чтобы узнать сколько она изготовила за 3 часа нужно количество деталей, изготовленных за час, умножить на количество часов.
40 ∙ 3 = 4 дес. ∙ 3 = 12 дес. = 120 (дет.) – изготовила вторая бригада за 3 часа.
Продолжаем рассуждение.
Производительность деталей двух бригад складывается из деталей каждой бригады, которую они изготовили.
90 + 120 = (10 + 80) + 120 = 10 + (80 + 120) = 10 + 200 = 210 (дет.) – изготовила 2 бригады за 3 часа.
Записываем ответ.
Ответ: 210 деталей.
Решение выражением:
30 ∙ 3 + 40 ∙ 3 = 210 (дет.) – изготовили всего,
где 30 ∙ 3 – изготавливала первая бригада за 1 час,
40 ∙ 3 – изготавливала вторая бригада за 1 час.
Номер 6.
Вычисли и сделай проверку.
Ответ:400 + 270 = 670
Проверка: 670 – 270 = 400
160 – 90 = 70
Проверка: 90 + 70 = 160
27 ∙ 3 = 81
Проверка: 81 : 3 = 27
98 : 14 = 7
Проверка: 14 ∙ 7 = 98
1) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
3) Вспомни как складывает и вычитать по разрядам.
Выполняем вычисления.
400 + 270 = (400 + 200) + 70 = 600 + 70 = 670
Число 270 представим в виде суммы 200 и 70. К числу 400 сначала прибавим 200, а потом число 70 и получим 670.
160 − 90 = 160 − (60 + 30) = (160 − 60) − 30 = 100 − 30 = 70
Число 90 представим в виде суммы чисел 60 и 30. Из числа 160 вначале вычтем 60, а потом число 30 и получим 70.
27 ∙ 3 = (20 + 7) ∙ 3 = 60 + 21 = 81
Число 27 представим в виде суммы чисел 20 и 7, по-отдельности умножим числа на 3, а потом полученные результаты сложим.
98 : 14 = ?
Пробуем в частном 5 и проверяем: 14 ∙ 5 = 70, 70 < 98, число 5 не подходит.
Пробуем в частном 6 и проверяем: 14 ∙ 6 = 84, 84 < 98, число 6 не подходит.
Пробуем в частном 7 и проверяем: 14 ∙ 7 = 98, 98 = 98, значит 98 : 14 = 7.
Ответ: 7.
Выполняем проверку.
400 + 270 = 670
Проверка: из суммы вычтем первое слагаемое, получим второе слагаемое.
670 − 400 = (600 − 400) + 70 = 270
160 − 90 = 70
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
70 + 90 = 70 + (30 + 60) = (70 + 30) + 60 = 160
27 ∙ 3 = 81
Проверка: произведение разделим на один из множителей, получим другой множитель.
81 : 3 = (60 + 27) : 3 = 20 + 7 = 27
98 : 14 = 7
Проверка: частное умножим на делитель, получим делимое.
14 ∙ 7 = (10 + 4) ∙ 7 = 70 + 28 = 98
Оформляем задание в тетрадь.
400 + 270 = (400 + 200) + 70 = 600 + 70 = 670
Проверка:
670 − 400 = 270
160 − 90 = 160 − (60 + 30) = (160 − 60) − 30 = 100 − 30 = 70
Проверка:
70 + 90 = 160
27 ∙ 3 = (20 + 7) ∙ 3 = 60 + 21 = 81
Проверка:
81 : 3 = 27
98 : 14 = 7
Проверка:
14 ∙ 7 = 98
Номер 7.
Найди длины отрезков АВ, АС, AD, если радиус каждой окружности 1 см 8 мм.

1-й способ решения:
1 см 8 мм = 18 мм
AВ = 18 ∙ 2 = 36 мм
AC = 18 ∙ 3 = 54 мм
AD = 18 ∙ 4 = 72 мм
2-й способ решения:
Отрезок АВ состоит из 2 радиусов.
18 мм · 2 = 36 мм = 3 см 6 мм – АВ
Отрезок АС состоит из 3 радиусов
18 мм · 3 = 54 мм = 5 см 4 мм – АС
Отрезок АD состоит из 4 радиусов
18 мм · 4 = 72 мм = 7 см 2 мм – AD
1) Помни о том, что окружность – это граница круга, расположенная на плоскости.
2) Радиус – отрезок, который соединяет центр окружности с любой точкой на окружности.
3) Помни, что 1 см = 10 мм.
Рассуждаем.
Так как радиус равен 1 см 8 мм, то:
АО = ОВ = ВС = СD = 1 см 8 мм = 18 мм – радиусы.
Продолжаем рассуждение.
Отрезок АВ состоит из суммы отрезков АО и ОВ. Сложим длины отрезков.
АВ = АО + ОВ = 18 мм + 18 мм = 36 мм = 3 см 6 мм
Отрезок АС состоит из суммы отрезков АВ и ВС. Сложим длины отрезков.
АС = АВ + ВС = 36 мм + 18 мм = 54 мм = 5 см 4 мм
Отрезок АD состоит из суммы отрезков Ас и СD. Сложим длины отрезков.
АD = АС + CD = 54 мм + 18 мм = 72 мм = 7 см 2 мм
Записываем ответ.
Ответ: AВ = 3 см 6 мм; AC = 5 см 4 мм; AD = 7 см 2 мм.
Рассуждаем.
Отрезок АВ состоит из 2 радиусов окружности, поэтому чтобы найти длину отрезка АВ нужно длину радиуса окружности умножить на 2.
18 мм ∙ 2 = 36 мм = 3 см 6 мм − АВ
18 ∙ 2 = (10 + 8) ∙ 2 = 20 + 16 = 36
Отрезок АС состоит из 3 радиусов окружности, поэтому чтобы найти длину отрезка АС нужно длину радиуса окружности умножить на 3.
18 мм ∙ 3 = 54 мм = 5 см 4 мм − АС
18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54
Отрезок АD состоит из 4 радиусов окружности, поэтому чтобы найти длину отрезка А D нужно длину радиуса окружности умножить на 4.
18 мм ∙ 4 = 72 мм = 7 см 2 мм − AD
18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72
Записываем ответ.
Ответ: AВ = 3 см 6 мм; AC = 5 см 4 мм; AD = 7 см 2 мм.
Задание внизу страницы
Вычисли и сделай проверку.
Ответ:320 – 200 = (300 + 20) – 200 = (300 – 200) + 20 = 120
Проверка:
320 – 120 = 200
200 + 120 = 320
140 + 50 = (100 + 40) + 50 = 100 + (40 + 50) = 190
Проверка:
190 – 50 = 140
190 – 140 = 50
91 : 7 = (49 + 42) : 7 = (49 : 7) + (42 : 7) = 7 + 6 = 13
Проверка:
7 · 13 = 91
91 : 13 = 7
3 · 29 = 3 · (20 + 9) = (3 · 20) + (3 · 9) = 60 + 27 = 87
Проверка:
87 : 3 = 29
87 : 29 = 3
1) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
3) Вспомни как складывает и вычитать по разрядам.
Выполняем вычисления.
320 − 200 = (300 − 200) + 20 = 100 + 20 = 120
Число 320 представим, как сумму чисел 300 и 20. Из числа 300 вначале вычтем 200, а потом к полученной разности прибавим 20 и получим 120.
140 + 50 = 100 + (40 +50) = 100 + 90 = 190
Число 140 представим в виде суммы 100 и 40. Вначале к числу 50 прибавим 40, а потом число 100 и получим 190.
91 : 7 = (70 + 21) : 7 = 10 + 3 = 13
Число 91 представим в виде суммы чисел 70 и 21, по-отдельности разделим числа на 7, а потом полученные результаты сложим.
3 ∙ 29 = 3 ∙ (20 + 9) = 60 + 27 = 87
Число 29 представим в виде суммы чисел 20 и 9, по-отдельности умножим числа на 3, а потом полученные результаты сложим.
Делаем проверку.
320 – 200 = 120
Проверка: к разности прибавим вычитаемое, получим уменьшаемое.
120 + 200 = (100 + 200) + 20 = 320
140 + 50 = 190
Проверка: из суммы вычтем первое слагаемое, получим второе слагаемое.
190 – 50 = 100 + (90 – 50) = 100 + 40 = 140
91 : 7 = 13
Проверка: частное умножим на делитель, получим делимое.
13 ∙ 7 = (10 + 3) ∙ 7 = 70 + 21 = 91
3 ∙ 29 = 87
Проверка: произведение разделим на один из множителей, получим другой множитель.
87: 3 = (60 + 27) : 3 = 20 + 9 = 29
Оформляем задание в тетрадь.
320 – 200 = (300 – 200) + 20 = 100 + 20 = 120
Проверка: 120 + 200 = 320
140 + 50 = 100 + (40 +50) = 100 + 90 = 190
Проверка:
190 – 50 = 140
91 : 7 = (70 + 21) : 7 = 10 + 3 = 13
Проверка: 13 ∙ 7 = 91
3 ∙ 29 = 3 ∙ (20 + 9) = 60 + 27 = 87
Проверка: 87: 3 = 27
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.