Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 46

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Расскажи, как получается каждое следующее число при счете? Присчитывай по одному, начиная с числа 100: 101, 102, ...
Ответ:Каждое следующее число получается прибавлением к предыдущему единицы.
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Каждое следующее число при счете получается путем прибавления единицы к данному числу.
Делаем проверку.
100 + 1 = 101
101 + 1 = 102
102 + 1 = 103
103 + 1 = 104 и так далее.
Номер 1.
Вставь пропущенные числа в каждом ряду.
1) 196, 197, 198, ..., ..., 201, 202, 203; 2) 903, 902, 901, ..., ..., 898, 897, 896.
Ответ:1) 196, 197, 198, 199, 200, 201, 202, 203; 2) 903, 902, 901, 900, 899, 898, 897, 896.
1) Вспомни, как получается каждое следующее число при счёте.
1) Вспомни, как получается каждое следующее число при счете.
2) Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Рассмотрим ряды.
Ряд 1. 196, 197, 198, …, …, 201, 202, 203.
К каждому предыдущему числу прибавили 1.
Ряд 2. 903, 902, 901, …, …, 898, 897, 896.
Из каждого предыдущего числа вычли 1.
Вычислим.
Найдём недостающие числа.
Ряд 1. 196, 197, 198, …, …, 201, 202, 203.
198 + 1 = 199
199 + 1 = 200.
Ряд 2. 903, 902, 901, …, …, 898, 897, 896.
901 – 1 = 900
900 – 1 = 899.
Оформляем задание в тетрадь.
1) 196, 197, 198, 199, 200, 201, 202, 203.
2) 903, 902, 901, 900, 899, 898, 897, 896.
Номер 2.
Ответ:319 + 1 = 320 940 – 1 = 939
760 – 1 = 759 439 + 1 = 440
509 + 1 = 510 800 – 1 = 799
690 – 1 = 689 299 + 1 = 300
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Каждое следующее число при счете получается путем прибавления единицы к данному числу.
Каждое предыдущее число образуется путем вычитания единицы из данного числа.
Выполняем вычисления и оформляем задание в тетрадь.
319 + 1 = 320
760 – 1 = 759
940 – 1 = 939
439 + 1 = 440
509 + 1 = 510
690 – 1 = 659
800 – 1 = 799
299 + 1 = 300
Номер 3.
Сколько всего квадратных сантиметров в 4 дм2? в 5 дм2? в 4 дм2 5 см2?
Ответ:4 дм2 = 400 см2 5 дм2 = 500 см2 4 дм2 5 см2 = 405 см2
Помни, что 1 дм2 = 100 см2.
Рассуждаем.
Так как 1 дм2 = 10 см ∙ 10 см = 100 см2, то:
4 дм2 = 4 ∙ 100 см2 = 400
5 дм2 = 5 ∙ 100 см2 = 500
4 дм2 5 см2 = 4 ∙ 100 см2 + 5 см2 = 400 см2 + 5 см2 = 405 см2
Оформляем задание в тетрадь.
4 дм2 = 400 см2
5 дм2 = 500 см2
4 дм2 5 см2 = 400 см2 + 5 см2 = 405 см2
Номер 4.
Купили 3 шапки по ☐ р. и столько же шарфов по ☐ р. Сколько стоила покупка? Подбери пропущенные числа и реши задачу разными способами.
Ответ:Купили 3 шапки по 5 рублей и столько же шарфов по 10 рублей. Сколько стоила покупка?

1-й способ решения:
1) 5 + 10 = 15 (р.) – стоит 1 комплект шапки и шарфа
2) 15 · 3 = 45 (р.) – стоила вся покупка
Ответ: 45 рублей стоили 3 шапки и 3 шарфа вместе.
2-й способ решения:
1) 5 · 3 = 15 (р.) – стоили шапки
2) 10 · 3 = 30 (р.) – стоили шарфы
3) 15 + 30 = 45 (р.) – стоила вся покупка
Ответ: 45 рублей стоят 3 шапки и 3 шарфа вместе.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость: количество = цена.
Стоимость : цена = количество.
Задача. Купили 3 шапки по 20 р. и столько же шарфов по 50 р. Сколько стоила покупка?
Оформляем условие в виде таблицы.

Рассуждаем.
Общая стоимость шапок складывается из стоимости каждой шапки. Стоимость каждой шапки одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
20 ∙ 3 = 60 (р.) – стоимость 3 шапок.
Продолжаем рассуждение.
Общая стоимость шарфов складывается из стоимости каждого шарфа. Стоимость каждого шарфа одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
50 ∙ 3 = 150 (р.) – стоимость 3 шарфов.
Продолжаем рассуждение.
Общая стоимость складывается из стоимости шапок и шарфов. Чтобы узнать общую стоимость, нужно сложить стоимость всех шапок и шарфов.
60 + 150 = 210 (р.) – общая стоимость.
Записываем ответ.
Ответ: 210 рублей.
Решение выражением:
20 ∙ 3 + 50 ∙ 3 = 210 (р.) – общая стоимость,
где 20 ∙ 3 – общая стоимость шапок,
50 ∙ 3 – общая стоимость шарфов.
Рассуждаем.
Стоимость набора «шапка и шарф» складывается из стоимости одной шапки и шарфа.
20 + 50 = 70 (р.) – стоимость набора «шапка и шарф».
Продолжаем рассуждение.
Общая стоимость набора «шапка и шарф» складывается из стоимости каждого набора. Стоимость каждого набора одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
70 ∙ 3 = 210 (р.) – общая стоимость.
Записываем ответ.
Ответ: 210 рублей.
Решение выражением:
(20 + 50) ∙ 3 = 70 ∙ 3 = 210 (р.) – общая стоимость,
где 20 + 50 – стоимость набора «шапка и шарф».
Номер 5.
Составь по выражениям задачи и реши их.
Ответ:Задача 1:

Купили 4 ручки по 12 р. и столько же карандашей по 8 р. Сколько стоит покупка?
12 ∙ 4 + 8 ∙ 4 = 80 (р.)
Ответ: покупка стоила 80 рублей.
Задача 2:

Купили 5 тетрадей по 7 рублей и столько же ластиков по 3 р. Сколько стоит покупка?
(7 + 3) ∙ 5 = 50 (р.)
Ответ: покупка стоит 50 р.
Задача 3:

Купили 3 блокнота по 23 р. и 2 ручки по 11 р. Сколько стоит покупка? 23 ∙ 3 + 11 ∙ 2 = 91 (р.) Ответ: покупка стоит 91 р.
1) Помни, чтобы умножить сумму на число, можно вычислить сумму и умножить её на число.
2) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
Выражение 12 ∙ 4 + 8 ∙ 4.
Задача. Купили в магазине 4 блокнота по 12 р. и столько же ручек по 8 р. Сколько стоит вся покупка?
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Общая стоимость блокнотов складывается из стоимости каждого блокнота. Стоимость каждого блокнота одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
4 ∙ 12 = 4 ∙ (10 + 2) = 40 + 8 = 48 (р.) – стоят 4 блокнота.
Продолжаем рассуждение.
Общая стоимость ручек складывается из стоимости каждой ручки. Стоимость каждой ручки одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
4 ∙ 8 = 32 (р.) – стоят 4 ручки.
Продолжаем рассуждение.
Общая стоимость складывается из стоимости блокнотов и ручек. Чтобы узнать общую стоимость, нужно сложить стоимость всех блокнотов и ручек.
48 + 32 = 80 (р.) – стоит вся покупка.
Записываем ответ.
Ответ: 80 рублей.
Решение выражением:
12 ∙ 4 + 8 ∙ 4 = 80 (р.) – стоимость всей покупки,
где 12 ∙ 4 – стоимость всех блокнотов,
8 ∙ 4 – стоимость всех ручек.
Выражение (7 + 3) ∙ 5.
Задача. Купили конфеты и шоколадки каждой по 5 штук. Конфеты стоят 3 рубля каждая, а шоколадка 7 рублей каждая. Сколько стоит вся покупка?
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Общая стоимость одной конфеты и одной шоколадки складывается из их стоимости.
7 + 3 = 10 (р.) – стоит набор «конфета и шоколадка»
Продолжаем рассуждение.
Общая стоимость набора «конфета и шоколадка» складывается из стоимости каждого набора. Стоимость каждого набора одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
10 ∙ 5 = 50 (р.) – вся стоимость.
Записываем ответ.
Ответ: 50 рублей.
Решение выражением:
(7 + 3) ∙ 5 = 50 (р.) – общая стоимость,
где 7 + 3 – стоимость набора «конфета и шоколад».
Выражение 23 ∙ 3 + 11 ∙ 2.
Задача. Купили в магазине 3 бантика по 23 рубля и 2 заколки по 11 рублей. Сколько стоит вся покупка?
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Общая стоимость бантиков складывается из стоимости каждого бантика. Стоимость каждого бантика одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
23 ∙ 3 = (20 + 3) ∙ 3 = 60 + 9 = 69 (р.) – стоимость 3 бантиков.
Продолжаем рассуждение.
Общая стоимость заколок складывается из стоимости каждой заколки. Стоимость каждой заколки одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
2 ∙ 11 = 22 (р.) – стоимость 2 заколок.
Продолжаем рассуждение.
Общая стоимость складывается из стоимости бантиков и заколок. Чтобы узнать общую стоимость, нужно сложить стоимость всех бантиков и заколок.
69 + 22 = 91 (р.) – стоит вся покупка.
Записываем ответ.
Ответ: 91 рубль.
Решение выражением:
23 ∙ 3 + 11 ∙ 2 = 91 (р.) – стоит вся покупка,
где 23 ∙ 3 – стоимость всех бантиков,
11 ∙ 2 – стоимость всех заколок.
Номер 6.
Ответ:

1) a ∙ 8, значит, значение a нужно умножить на 8, т.е. увеличить в 8 раз.
2) b : 7, значит, значение b разделить на 8, т.е. уменьшить число в 8 раз.
Промежуточные вычисления.
Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.
а ∙ 8, если:
а = 12, то 12 ∙ 8 = (10 + 2) ∙ 8 = 80 + 16 = 96
а = 11, то 11 ∙ 8 = 88
а = 10, то 10 ∙ 8 = 80
а = 9, то 9 ∙ 8 = 72
Заполним таблицу.
.jpg)
Промежуточные вычисления.
Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.
b : 8, если:
b = 32, то 32 : 8 = 4
b = 48, то 48 : 8 = 6
b = 56, то 56 : 8 = 7
b = 64, то 64 : 8 = 8
Заполним таблицу.
.jpg)
Номер 7.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
2 1
90 − 48 : 3 = 74
1) 48 : 3 = (30 + 18) : 3 = 10 + 6 = 16
2) 90 − 16 = 74
1 2
(90 − 48) : 3 = 14
1) 90 – 48 = 42
2) 42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
1 2
(56 + 28) : 14 = 6
1) 56 + 28 = 84
2) 84 : 14 = 6 – вычисление методом подбора.
2 1
56 + 28 : 14 = 58
1) 28 : 14 = 2 – вычисление методом подбора.
2) 56 + 2 = 58
1 3 2
9 · 9 – 8 · 5 = 41
1) 9 ∙ 9 = 81
2) 8 ∙ 5 = 40
3) 81 – 40 = 41
2 1 3
9 · (9 – 8) · 5 = 45
1) 9 – 8 = 1
2) 9 ∙ 1 = 9
3) 9 ∙ 5 = 45
Оформляем задание в тетрадь.
2 1
90 − 48 : 3 = 90 − 16 = 74
1 2
(90 − 48) : 3 = 42 : 3 = 14
1 2
(56 + 28) : 14 = 84 : 14 = 6
2 1
56 + 28 : 14 = 56 + 2 = 58
1 3 2
9 · 9 – 8 · 5 = 81 – 40 = 41
2 1 3
9 · (9 – 8) · 5 = 9 · 1 · 5 = 45
Номер 8.
1) Начерти два квадрата: сторона одного 3 см, сторона другого в 3 раза больше. Во сколько раз площадь второго квадрата больше площади первого? 2) Во сколько раз периметр второго квадрата больше периметра первого?
Ответ:
1) Сторона одного квадрата 3 см, сторона другого - в 3 раза больше. Во сколько раз площадь второго квадрата больше площади первого?

1) 3 ∙ 3 = 9 (см2) – площадь первого квадрата. 2) 3 ∙ 3 = 9 (см) – сторона второго квадрата. 3) 9 ∙ 9 = 81 (см2) – площадь второго квадрата. 4) 81 : 9 = 9 (р.) – площадь второго квадрата больше, чем площадь первого. Ответ: в 9 раз площадь второго квадрата больше, чем площадь первого; 2) Во сколько раз периметр второго квадрата больше периметра первого?

1) 3 ∙ 4 = 12 (см) – периметр первого квадрата. 2) 9 ∙ 4 = 36 (см) – периметр второго квадрата. 3) 36 : 12 = 3 (р.) – периметр второго квадрата больше, чем периметр первого. Ответ: в 3 раза периметр второго квадрата больше, чем периметр первого.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Периметр – сумма длин всех сторон.
Рассуждаем.
Сторона второго квадрата в 3 раза больше стороны первого. Значит, чтобы найти сторону второго квадрата, нужно сторону первого квадрата умножить на 3.
3 см ∙ 3 = 9 см – длина второго квадрата.
Начертим.
Начертим два квадрата со стороной 3 см и стороной 9 см.
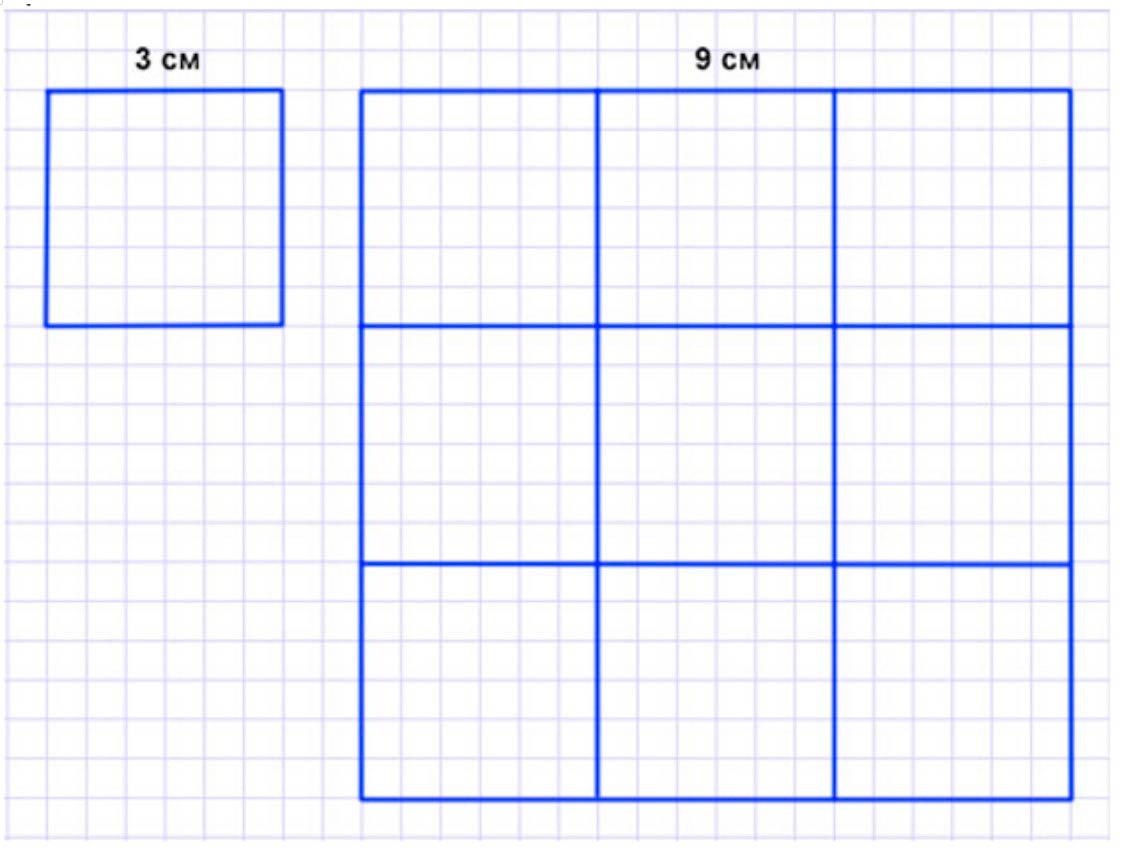
Продолжаем рассуждение.
Чтобы вычислить площадь квадрата, нужно длину стороны умножить на сторону.
3 см ∙ 3 см = 9 см2 – площадь первого квадрата.
9 см ∙ 9 см = 81 см2 – площадь второго квадрата.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
81 см2 : 9 см2 = 9 (раз) – во сколько раз площадь второго квадрата больше площади первого.
Записываем ответ.
Ответ: в 9 раз.
Рассуждаем.
Так как у квадрата все стороны равны, то чтобы найти периметр квадрата нужно его сторону умножить на 4.
3 см ∙ 4 = 12 (см) – периметр первого квадрата.
9 см ∙ 4 = 36 (см) – площадь второго квадрата.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
36 см : 12 см = 3 (раза) – во сколько раз периметр второго квадрата больше периметра первого квадрата.
Записываем ответ.
Ответ: в 3 раза.
Номер 9.
Ответ:
90 : 9 ∙ 1 = 10 * 1 = 10
80 : 8 ∙ 0 = 10 * 0 = 0
(84 − 77) : 1 = 7 : 1 = 7
(9 − 9) : 8 = 0 : 8 = 0
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, на которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Рассуждаем.
90 : 9 ∙ 1 = 90 : 9 = 10
Вторым действием значение умножают на 1, значит значение выражения не изменится.
80 : 8 ∙ 0 = 0
Значение выражения умножают на 0, значение всего выражения будет равно 0.
(84 – 77) : 1 = 84 – 77 = 7
Вторым действием значение выражения делят на 1, значит значение выражения не изменится.
(9 – 9) : 8 = 0 : 8 = 0
В первом действии значение выражения равно 0, а при делении 0 на любое число, выражение равно 0.
Оформляем задание в тетрадь.
90 : 9 ∙ 1 = 10
80 : 8 ∙ 0 = 0
(84 – 77) : 1 = 7
(9 – 9) : 8 = 0
Номер 10.
Сравни произведения, не вычисляя их значение.
1) 20 ∙ 3 ∙ 4 2) 8 ∙ 44 ∙ 20 3) 4 ∙ 3 ∙ 10
Ответ:8 ∙ 44 ∙ 20 > 20 ∙ 3 ∙ 4 > 4 ∙ 3 ∙ 10
1) Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением.
2) Помни о зависимости между компонентами и результатом действия умножения.
Рассуждаем.
Сравним 1 и 2 выражения:
20 = 20, 3 < 8, 4 < 44.
Значит, 20 ∙ 3 ∙ 4 < 8 ∙ 44 ∙ 20
Сравним 2 и 3 выражения:
8 > 4, 44 > 3, 20 > 10.
Значит, 8 ∙ 44 ∙ 20 > 4 ∙ 3 ∙ 10
Сравним 1 и 3 выражения:
20 > 10, 3 = 3, 2 = 2.
Значит, 20 ∙ 3 ∙ 4 > 4 ∙ 3 ∙ 10.
Делаем вывод.
2 выражение > 1 выражение > 3 выражение.
8 ∙ 44 ∙ 20 > 20 ∙ 3 ∙ 4 > 4 ∙ 3 ∙ 10.
Задание внизу страницы
Заполни пропуски.
Ответ:901, 900, 899, 898, 897, 896, 895, 894
1) Вспомни, как получается каждое предыдущее число.
2) Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Из каждого предыдущего числа вычли 1.
Каждое предыдущее число образуется путем вычитания единицы из данного числа.
Вычислим.
Найдём недостающие числа.
900 – 1 = 899
899 – 1 = 898
897 – 1 = 896
896 – 1 = 895
Оформляем задание в тетрадь.
901, 900, 899, 898, 897, 896, 895, 894.
Задание на полях страницы
Заполни магический квадрат, используя только числа 1, 2, 3:


1 + 2 + 3 = 3 + 3 = 6
2 + 3 + 1 = 5 + 1 = 6
3 + 1 + 2 = 4 + 2 = 6
1 + 2 + 3 = 3 + 3 = 6
2 + 3 + 1 = 5 + 1 = 6
3 + 1 + 2 = 4 + 2 = 6
1 + 3 + 2 = 4 + 2 = 6
3 + 3 + 3 = 6 + 3 = 9
Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Рассуждаем.
Так как можно использовать только числа 1, 2 и 3, то сумма в данном магическом квадрате должна быть равна 1 + 2 + 3 = 6.
Оформляем задание в тетрадь.
Вам представлены 2 варианта, выбери себе 1 вариант решения.
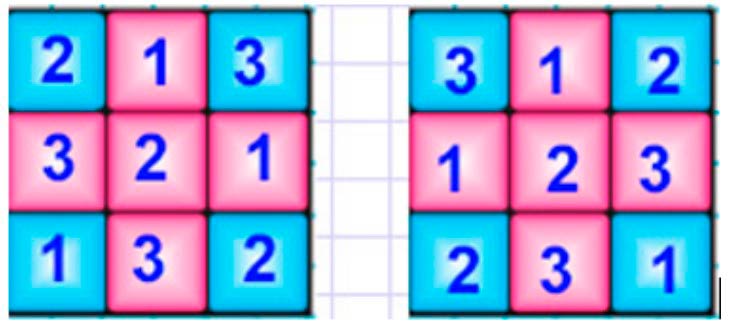
Номер 1.
Замени числа суммой разрядных слагаемых.
Ответ:309 = 300 + 9
806 = 800 + 6
970 = 900 + 70
250 = 200 + 50
222 = 200 + 20 + 2
346 = 300 + 40 + 6
Вспомни, как образуются и называются трёхзначные числа.
Рассуждаем.
309 = 3 сот. + 0 дес. + 9 ед. = 300 + 9
Разряд десятков отсутствует.
806 = 8 сот. + 0 дес. + 6 ед. = 800 + 6
Разряд десятков отсутствует.
Разряд единиц отсутствует.
250 = 2 сот. + 5 дес. + 0 ед. = 200 + 50
Разряд единиц отсутствует.
222 = 2 сот. + 2 дес. + 2 ед. = 200 + 20 + 2
Все разряды присутствуют.
346 = 3 сот. + 4 дес. + 6 ед. = 300 + 40 + 6
Все разряды присутствуют.
Оформляем задание в тетрадь.
309 = 300 + 9
806 = 800 + 6
970 = 900 + 70
250 = 200 + 50
222 = 200 + 20 + 2
346 = 300 + 40 + 6
Номер 2.
Рассмотри суммы. Выпиши числа, которые представлены в виде суммы разрядных слагаемых.
Ответ:600 + 40 + 5 = 645 800 + 20 = 820 800 + 2 = 802
1) Вспомни как образуются и называются трёхзначные числа.
2) Повтори как разложить число на разрядные слагаемые.
Рассуждаем.
Рассмотрим выражения.
960 + 6 – данное выражение – это просто сумма чисел, а не сумма разрядных слагаемых, так как в числе 960 есть и сотни, и десятки.
349 + 1 – данное выражение – это просто сумма чисел, а не сумма разрядных слагаемых, так как в числе 349 есть и сотни, и десятки, и единицы.
600 + 40 + 5 – данное выражение представляет собой сумму разрядных слагаемых, то есть сумма сотен, десятков и единиц.
600 + 300 + 9 – данное выражение – это просто сумма чисел, а не сумма разрядных слагаемых, так как 6 сотен и 3 сотни – это числа одного разряда, которые в сумме дадут число 9 того же разряда.
800 + 20 – данное выражение представляет собой сумму разрядных слагаемых, то есть сумма сотен и десятков.
800 + 2 – данное выражение представляет собой сумму разрядных слагаемых, то есть сумма сотен и единиц.
Оформляем задание в тетрадь.
600 + 40 + 5 = 645
800 + 20 = 820
800 + 2 = 802
Номер 3.
Мама собрала 8 корзинок вишни, по 3 кг в каждой корзинке. Из 14 кг она сварила варенье. Сколько килограммов вишни осталось?
Ответ:Собрала – 8 корзин по 3 кг Использовала – 14 кг Осталось – ? кг 1) 3 ∙ 8 = 24 (кг) – вишни было собрано. 2) 24 – 14 = 10 (кг) Ответ: 10 кг вишни осталось.
«8 корзинок по 3 кг в каждой» – вычисляется умножением.
Оформляем краткую запись.
Собрала – 8 корзин по 3 кг
Использовала – 14 кг
Осталось – ? кг
Рассуждаем.
Чтобы узнать, сколько всего вишни собрала мама, нужно вес вишни в одной корзинке умножить на количество корзинок.
3 ∙ 8 = 24 (кг) – вишни собрала мама.
Продолжаем рассуждение.
Чтобы узнать сколько вишни осталось, нужно из общего количества вишни вычесть количество вишни, которое использовали.
24 – 14 = 10 (кг) – вишни осталось.
Записываем ответ.
Ответ: 10 кг вишни осталось.
Номер 4.
На рисунке показана часть паркета, которую надо заменить. Каждый квадрат паркета составлен из четырех дощечек. Сколько всего нужно дощечек? Объясни, как решали задачу Коля и Юра.

4 · 6 + 4 · 3 = 24 + 12 = 36 (д.)
Коля количество дощечек в одном квадрате умножил на количество квадратов в каждом ряду отдельно, а затем полученные результаты сложил.
4 · (6 + 3) = 4 · 9 = 36 (д.)
Юра вначале нашёл количество квадратов паркета на замену, а потом умножил количество дощечек в одном квадрате на общее количество квадратов.
Ответ: 36 дощечек нужно.
1) Помни, чтобы умножить сумму на число, можно вычислить сумму и умножить её на число.
2) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Рассмотрим решение Коли.
4 ∙ 6 = 24 – количество дощечек в одном квадрате умножил на количество квадратов в первом ряду;
4 ∙ 3 = 12 – количество дощечек в одном квадрате умножил на количество квадратов во втором ряду;
4 ∙ 6 + 4 ∙ 3 = 24 + 12 = 36 – общее количество дощечек.
Продолжаем рассуждение.
Рассмотрим решение Юры.
6 + 3 = 9 – общее количество квадратов;
4 ∙ (6 + 3) = 4 ∙ 9 = 36 – общее количество дощечек.
Оформляем задание в тетрадь.
Решение Коли: 4 ∙ 6 + 4 ∙ 3 = 24 + 12 = 36 (д.) – нужно на паркет.
Коля количество дощечек в одном квадрате, умножил на количество квадратов в каждом ряду отдельно, а затем полученные результаты сложил.
Решение Юры: 4 ∙ (6 + 3) = 4 ∙ 9 = 36 (д.) – нужно на паркет.
Юра вначале нашёл количество квадратов паркета на замену, а потом умножил количество дощечек в одном квадрате на общее количество квадратов.
Ответ: 36 дощечек нужно.
Номер 5.
Ответ:14 ∙ 6 : 4 = 21
18 ∙ 4 : 6 = 12
19 ∙ 5 : 1 = 95
17 ∙ 3 + 2 ∙ 15 = 81
18 ∙ 5 – 3 ∙ 16 = 42
16 ∙ 4 – 4 ∙ 12 = 16
(48 + 16) : 4 = 16
(75 – 25) : 5 = 10
(96 – 32) : 2 = 32
1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1 2
14 · 6 : 4 = 21
1) 14 ∙ 6 = (10 + 4) ∙ 6 = 60 + 24 = 84
2) 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21
1 2
18 ∙ 4 : 6 = 12
1) 18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72
2) 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12
1 2
19 ∙ 5 : 1 = 95
1) 19 ∙ 5 = (10 + 9) ∙ 5 = 50 + 45 = 95
2) 95 : 1 = 95
1 3 2
17 ∙ 3 + 2 ∙ 15 = 81
1) 17 ∙ 3 = (10 + 7) ∙ 3 = 30 + 21 = 51
2) 2 ∙ 15 = 2 ∙ (10 + 5) = 20 + 10 = 30
3) 51 + 30 = 81
1 3 2
18 ∙ 5 − 3 ∙ 16 = 42
1) 18 ∙ 5 = (10 + 8) ∙ 5 = 50 + 40 = 90
2) 3 ∙ 16 = 3 ∙ (10 + 6) = 30 + 18 = 48
3) 90 – 48 = 42
1 3 2
16 ∙ 4 – 4 ∙ 12 = 16
1) 16 ∙ 4 = (10 + 6) ∙ 4 = 40 + 24 = 64
2) 4 ∙ 12 = 4 ∙ (10 + 2) = 40 + 8 = 48
3) 64 – 48 = 16
1 2
(48 + 16) : 4 = 16
1) 48 + 16 = 64
2) 64 : 4 = (40 + 24) : 4 = 10 + 6 = 16
1 2
(75 – 25) : 5 = 10
1) 75 – 25 = 50
2) 50 : 5 = 10
1 2
(96 – 32) : 2 = 32
1) 96 – 32 = 64
2) 64 : 2 = (60 + 4) : 2 = 60 : 2 + 4 : 2 = 30 + 2 = 32
Оформляем задание в тетрадь.
1 2
14 · 6 : 4 = 84 : 4 = 21
1 2
18 ∙ 4 : 6 = 72 : 6 = 12
1 2
19 ∙ 5 : 1 = 95 : 1 = 95
1 3 2
17 ∙ 3 + 2 ∙ 15 = 51 + 30 = 81
1 3 2
18 ∙ 5 − 3 ∙ 16 = 90 − 48 = 42
1 3 2
16 ∙ 4 – 4 ∙ 12 = 64 – 48 = 16
1 2
(48 + 16) : 4 = 64 : 4 = 16
1 2
(75 – 25) : 5 = 50 : 5 = 10
1 2
(96 – 32) : 2 = 64 : 2 = 32
Номер 6.
Как переложить 2 палочки, чтобы получилось 5 одинаковых квадратов?


Для того, чтобы выполнить задание, удобнее провести реальные действия с предметами, например, со спичками.
Рассмотрим.
Нужно две палочки из бокового угла переложить в середину.
-(2024).jpg)
Получится 5 одинаковых квадратов.
Оформляем задание в тетрадь.
-(2024).jpg)
Задание внизу страницы
Замени число суммой разрядных слагаемых.
Ответ:648 = 600 + 40 + 8 707 = 700 + 7 830 = 800 + 30
1) Вспомни как образуются и называются трёхзначные числа.
2) Повтори как разложить число на разрядные слагаемые.
Рассуждаем.
Рассмотрим числа.
648 – число состоит из 6 сот., 4 дес. и 8 ед.
648 = 6 сот. + 4 дес. + 8 ед. = 600 + 40 + 8
Все разряды присутствуют.
707 – число состоит из 7 сот. и 7 ед.
707 = 7 сот. + 0 дес. + 7 ед. = 700 + 7
Разряд десятков отсутствует.: 00
830 – число состоит из 8 сот. и 3 дес.
830 = 8 сот. + 3 дес. + 0 ед. = 800 + 30
Разряд единиц отсутствует.
Оформляем задание в тетрадь.
648 = 600 + 40 + 8
707 = 700 + 7
830 = 800 + 30
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.