Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 45

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 5.
Ответ:125 см = 1 м 2 дм 5 см 86 мм = 8 см 6 мм 540 см = 5 м 4 дм 42 дм = 4 м 2 дм
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм
Рассмотрим выражения.
125 см = 100 см + 20 см + 5 см = 1 м 2 дм 5 см,
так как 100 см = 1 м и 20 см = 2дм;
540 см = 500 см + 40 см + 0 см = 5 м 4 дм,
так как 500 см = 5 м и 40 см = 4 дм;
86 мм = 80 мм + 6 мм = 8 см 6 мм,
так как 80 мм = 8 см;
42 дм = 40 дм + 2 дм = 4 м 2 дм,
так как 40 дм = 4 м.
Оформляем задание в тетрадь.
125 см = 1 м 2 дм 5 см
540 см = 5 м 4 дм
86 мм = 8 см 6 мм
42 дм = 4 м 2 дм
Номер 6.
Составь по таблице задачу и реши ее.

В столовой за 6 дней израсходовали 72 кг картофеля, в последующие дни израсходовали 60 кг картофеля. За сколько дней израсходовали 60 кг картофеля, если расходовали в день одинаковое количество картофеля? 1) 72 : 6 = 12 (кг) – картофеля расходовали в 1 день. 2) 60 : 12 = 5 (д.) – израсходовали 60 кг картофеля. Ответ: 60 кг картофеля израсходовали за 5 дней.
Данная задача: вида «расход в день, количество дней, общий расход» характеризуется зависимостями между элементами:
Расход на день · количество дней = общий расход.
Общий расход : расход в день = количество дней.
Общий расход : количество дней = расход в день.
Составляем задачу.
Задача: В пекарне израсходовали за 6 дней 72 кг муки. При одинаковом расходе за сколько дней израсходуют 60 кг муки?
Рассуждаем.
Каждый день расходуется одинаковое количество муки.
Чтобы узнать расход в день, нужно общий расход разделить на количество дней.
72 : 6 = (60 + 12) : 6 = 10 + 2 = 12 (кг) – муки за 1 день.
Продолжаем рассуждение.
Каждый день расходуется 12 кг муки. Чтобы узнать на сколько дней хватит 60 кг муки, нужно общее количество муки разделить на расход в день.
60 : 12 = 5 (дн.) – израсходовали 60 кг муки.
Записываем ответ.
Ответ: за 5 дней.
Решение выражением:
60 : (72 : 6) = 5 (дн.) – израсходовали 60 кг муки, где 72 : 6 – расход в день.
Номер 7.
В столовой 5 дней расходовали по 12 кг крупы, а 2 дня – по 9 кг. Сколько крупы израсходовали за все эти дни?
Запиши задачу в таблицу и реши ее.

1-й способ решения:
1) 12 · 5 = 60 (кг) – крупы израсходовали за 5 дней.
2) 9 · 2 = 18 (кг) – крупы израсходовали за 2 дня.
3) 60 + 18 = 78 (кг)
Ответ: 78 кг крупы израсходовали за все эти дни.
2-й способ решения:
5 · 12 + 2 · 9 = 60 + 18 = 78 (кг) – всего за 2 дня.
Ответ: 78 кг.
Данная задача: вида «расход в день, количество дней, общий расход» характеризуется зависимостями между элементами:
Расход на день · количество дней = общий расход.
Общий расход : расход в день = количество дней.
Общий расход : количество дней = расход в день.
Оформляем условие в виде таблицы.

Рассуждаем.
В столовой 5 дней расходовали по 12 кг крупы, значит одинаковое количество. Чтобы узнать это, нужно расход крупы в день умножить на количество дней.
5 ∙ 12 = 5 ∙ (10 + 2) = 50 + 10 = 60 (кг) – крупы израсходовали за 5 дней.
Продолжаем рассуждение.
В столовой 2 дня расходовали по 9 кг крупы, значит одинаковое количество. Чтобы узнать это, нужно расход крупы в день умножить на количество дней.
2 ∙ 9 = 18 (кг) – крупы израсходовали за 2 дня.
Продолжаем рассуждение.
Общий расход складывается из расхода за 5 дней и расхода за 2 дня. Значит, эти значения нужно сложить.
60 + 18 = 78 (кг) – общий расход.
Записываем ответ.
Ответ: 78 кг крупы.
Решение выражением:
5 ∙ 12 + 2 ∙ 9 = 60 + 18 = 78 (кг) – общий расход крупы,
где 5 ∙ 12 – израсходовали за 5 дней;
2 ∙ 9 – израсходовали за 2 дня.
Номер 8.
Начерти в тетради прямоугольник со сторонами 3 см и 6 см. Раскрась его третью часть и вычисли ее площадь.
Ответ:
1) 6 ∙ 3 = 18 (см2) - площадь прямоугольника
2) 18 : 3 = 6 (см2) - площадь закрашенной части
Ответ: площадь закрашенной части составляет 6 см2
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Начертим прямоугольник.
Начертим прямоугольник со сторонами 6 см и 3 см.
.jpg)
Рассуждаем.
Найдём часть, которую нужно закрасить.
Одна третья часть, значит прямоугольник разделили на 3 части и взяли одну такую часть.
Разделим прямоугольник по горизонтали.
.jpg)
Продолжаем рассуждение.
Нужно найти площадь закрашенной части. Значит, нужно найти площадь прямоугольника со сторонами 6 см и 1 см.
6 ∙ 1 = 6 (см2) – площадь закрашенной части.
Записываем ответ.
Ответ: 6 см2.
Рассуждаем.
Найдём часть, которую нужно закрасить.
Одна третья часть, значит прямоугольник разделили на 3 части и взяли одну такую часть.
Разделим прямоугольник по вертикали.
.jpg)
Продолжаем рассуждение.
Нужно найти площадь закрашенной части. Значит, нужно найти площадь прямоугольника со сторонами 2 см и 3 см.
3 ∙ 2 = 6 (см2) – площадь закрашенной части.
Записываем ответ.
Ответ: 6 см2.
Номер 9.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
3 2 1
80 − 40 : (5 + 35)
2 1 3
57 − 27 : 3 + 24
1 3 2
60 : 3 + 2 · 6
2 1 3
60 : (3 + 2) · 6
1 2
(49 − 42) : 7
1 2
(54 − 24) : 6
Выполняем вычисления по действиям.
3 2 1
80 − 40 : (5 + 35) = 79
1) 5 + 35 = 40
2) 40 : 40 = 1
3) 80 − 79 = 79
2 1 3
57 − 27 : 3 + 24 = 72
1) 27 : 3 = 9
2) 57 − 9 = 48
3) 48 + 24 = 72
1 3 2
60 : 3 + 2 · 6 = 32
1) 60 : 3 = 6 дес. : 3 = 2 дес. = 20
2) 2 ∙ 6 = 12
3) 20 + 12 = 32
2 1 3
60 : (3 + 2) · 6 = 72
1) 3 + 2 = 5
2) 60 : 5 = (50 + 10) : 5 = 10 + 2 = 12
3) 12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72
1 2
(49 − 42) : 7 = 1
1) 49 − 42 = 7
2) 7 : 7 = 1
1 2
(54 − 24) : 6 = 5
1) 54 − 24 = 30
2) 30 : 6 = 5
Оформляем задание в тетрадь.
3 2 1
80 − 40 : (5 + 35) = 80 − 40 : 40 − 1 = 79
2 1 3
57 − 27 : 3 + 24 = 57 − 9 + 24 = 48 + 24 = 72
1 3 2
60 : 3 + 2 · 6 = 20 + 12 = 32
2 1 3
60 : (3 + 2) · 6 = 60 : 5 · 6 = 12 · 6 = 72
1 2
(49 − 42) : 7 = 7 : 7 = 1
1 2
(54 − 24) : 6 = 30 : 6 = 5
Номер 10.
Найди частное и остаток и выполни проверку.
Ответ:51 : 7 = 7 (ост. 2)
Проверка:
1) 2 < 7
2) 7 · 7 + 2 = 51
59 : 9 = 6 (ост. 5)
Проверка:
1) 5 < 9
2) 9 · 6 + 5 = 59
78 : 11 = 7 (ост. 1)
Проверка:
1) 1 < 11
2) 11 · 7 + 1 = 78
60 : 25 = 2 (ост. 10)
Проверка:
1) 10 < 25
2) 25 · 2 + 10 = 60
37 : 10 = 3 (ост. 7)
Проверка:
1) 7 < 10
2) 10 · 3 + 7 = 37
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Вычисляем.
51 : 7 = ?
51 не делится на 7 без остатка. Вспомним, какое самое большое число до 51 делится на 7 без остатка. Это 49.
Найдём частное: 49 : 7 = 7.
Найдём остаток: 51 – 49 = 2.
Значит, 51 : 7 = 7 (ост. 2)
59 : 9 = ?
59 не делится на 9 без остатка. Вспомним, какое самое большое число до 59 делится на 9 без остатка. Это 54.
Найдём частное: 54 : 9 = 6.
Найдём остаток: 59 – 54 = 5.
Значит, 59 : 9 = 6 (ост. 5)
78 : 11 = ?
Если трудно вспомнить самое большое число до 77, которое делится на 11 без остатка, то частное можно найти способом подбора.
Пробуем в частном 6.
Проверим: 11 ∙ 6 = 66.
Найдём остаток и сравним его с делителем: 78 – 66 = 12, 12 > 11, значит 6 мало.
Пробуем в частном 7.
Проверим: 11 ∙ 7 = 77.
Найдем остаток и сравним его с делителем: 78 – 77 = 11, 1 < 11, значит частное 7, а остаток 1.
Значит, 77 : 11 = 7 (ост. 1)
60 : 25 = ?
Если трудно вспомнить самое большое число до 60, которое делится на 25 без остатка, то частное можно найти способом подбора.
Пробуем в частном 2.
Проверим: 25 ∙ 2 = 50.
Найдём остаток и сравним его с делителем: 60 – 50 = 10, 10 < 25, значит частное 2, а остаток 10.
Значит, 60 : 25 = 2 (ост. 10)
37 : 10 = ?
37 не делится на 10 без остатка. Вспомним, какое самое большое число до 37 делится на 10 без остатка. Это 30, так как 3 ∙ 10 = 30
Найдём частное: 30 : 10 = 3 дес. : 1дес. = 3
Найдём остаток: 37 – 30 = 7.
Значит, 37 : 10 = 3 (ост. 7)
Сделаем проверку.
Чтобы сделать проверку нужно:
1) убедиться, что остаток меньше делителя;
2) частное умножить на делитель и прибавить к произведению остаток, должно получиться делимое.
Если хотя бы один пункт не выполняется, то деление выполнено не верно.
51 : 7 = 7 (ост. 2)
Проверка:
1) 7 ∙ 7 = 49 – неполное делимое
2) 49 + 2 = 51 – делимое
51 = 51
3) 2 < 7 – остаток должен быть меньше делителя.
59 : 9 = 6 (ост. 5)
Проверка:
1) 9 ∙ 6 = 54 – неполное делимое
2) 54 + 5 = 59 – делимое
59 = 59
3) 5 < 9 – остаток должен быть меньше делителя.
78 : 11 = 7 (ост. 1)
Проверка:
1) 11 ∙ 7 = 77 – неполное делимое
2) 77 + 1 = 78 – делимое
78 = 78
3) 1 < 11 – остаток должен быть меньше делителя.
60 : 25 = 2 (ост. 10)
Проверка:
1) 25 ∙ 2 = 50 – неполное делимое
2) 50 + 10 = 60 – делимое
60 = 60
3) 10 < 25 – остаток должен быть меньше делителя.
37 : 10 = 3 (ост. 7)
Проверка:
1) 10 ∙ 3 = 30 – неполное делимое
2) 30 + 7 = 37 – делимое
37 = 37
3) 7 < 10 – остаток должен быть меньше делителя.
Оформляем задание в тетрадь.
51 : 7 = 7 (ост. 2)
Проверка:
7 ∙ 7 + 2 = 51
2 < 7
59 : 9 = 6 (ост. 5)
Проверка:
6 ∙ 9 + 5 = 59
5 < 9
78 : 11 = 7 (ост. 1)
Проверка:
7 ∙ 11 + 1 = 78
1 < 11
60 : 25 = 2 (ост. 10)
Проверка:
2 ∙ 25 + 10 = 60
10 < 25
37 : 10 = 3 (ост. 7)
Проверка:
3 ∙ 10 + 7 = 37
7 < 10
Номер 11.
Используя пары числовых выражений, составь верные равенства:
60 : 4; 48 : 3; 90 : 6; 84 : 7; 36 : 3.
Ответ:60 : 4 = 90 : 6 84 : 7 = 36 : 3
1) Прежде, чем составлять верные равенства, вычисли значение каждого выражения.
2) Равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знака равно.
Вычислим значения выражений.
Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
60 : 4 = (40 + 20) : 4 = 10 + 5 = 15
48 : 3 = (30 + 18) : 3 = 10 + 6 = 16
90 : 6 = (60 + 30) : 6 = 10 + 5 = 15
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
36 : 3 = (30 + 6) : 3 = 10 + 2 = 12
Составим равенства.
60 : 4 = 90 : 6
15 = 15
84 : 7 = 36 : 3
12 = 12
Номер 12.
Начерти в тетради две такие фигуры.
Проведи в каждой из них два отрезка так, чтобы на чертеже, кроме данной фигуры, стало: 1) 2 треугольника, 1 прямоугольник и 2 пятиугольника; 2) 2 треугольника и 6 четырехугольников.


1) Вспомни какие бывают многоугольники.
2) Вспомни как обозначать геометрические фигуры буквами.
Начертим.
Начертим фигуру, обозначим её буквами и проведем два отрезка.
.jpg)
Рассмотрим фигуру.
Получилось:
2 треугольника: ВСК и АНО
1 прямоугольник: АВКН
2 пятиугольника: ОАВКН и ВСКНА.
Начертим.
Начертим фигуру, обозначим её буквами и проведем два отрезка.
.jpg)
Рассмотрим фигуру.
Получилось:
2 треугольника: СКМ и КЕР.
6 четырехугольников: СЕТМ, СЕРХ, РМТЕ, РМСХ, МКЕТ, СКРТ.
Задание внизу страницы
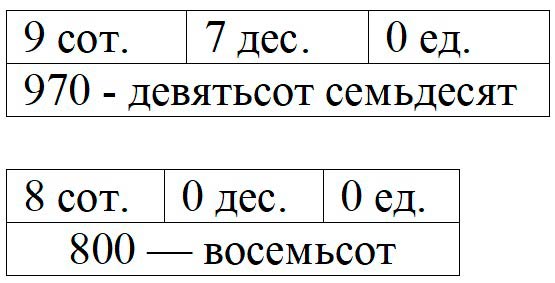
Запиши и прочитай:
Ответ:9 сот. 7 дес. 0 ед. = 970 (девятьсот семьдесят) 8 сот. 0 дес. 0 ед. = 800 (восемьсот)
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
9 сот. 7 дес. 0 ед. = 9 ∙ 1 сот. + 7 ∙ 1 дес. + 0 ед. = 9 ∙ 100 + 7 ∙ 10 + 0 = 900 + 70 + 0 = 970 — девятьсот семьдесят.
8 сот. 0 дес. 0 ед.= 8 ∙ 1 сот. + 0 ∙ 1 дес. + 0 ед. = 8 ∙ 100 + 0 ∙ 10 + 0 = 800 + 0 + 0 = 800 — восемьсот.
Оформляем задание в тетрадь.
Задание на полях страницы
Найди лишнее выражение:
7 · 9 6 · 7 8 · 6 7 · 7 4 · 7 7 · 5 7 · 10
Ответ:8 ∙ 6, так как значение этого выражения не делится на 7.
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим выражения.
7 ∙ 9 = 63
6 ∙ 7 = 42
8 ∙ 6 = 48
7 ∙ 7 = 49
4 ∙ 7 = 28
7 ∙ 5 = 35
7 ∙ 10 = 70
Делаем вывод.
Выражение 8 ∙ 6 = 48 – лишнее, так как в произведении нет множителя 7, то есть данное произведение не делится на 7, а остальные делятся на 7.
Номер 1.
Увеличь в 10 раз числа: 8, 12, 35. Уменьши в 100 раз числа: 700, 400, 100. Уменьши в 10 раз числа: 840, 900, 360.
Ответ:80, 120, 350. 7, 4, 1. 84, 90, 36.
Повтори, как можно получить число, которое больше или меньше данного в 10 раз; в 100 раз.
Рассуждаем.
Увеличить число в 10 раз, это значит данное число нужно умножить на 10.
Чтобы умножить число на 10, нужно к нему справа приписать один нуль.
8 ∙ 10 = 80
12 ∙ 10 = 120
35 ∙ 10 = 350
Продолжаем рассуждение.
Уменьшить число в 100 раз, значит число нужно разделить на 100.
Чтобы разделить число на 100, нужно убрать у него справа два нуля.
700 : 100 = 7
400 : 100 = 4
100 : 100 = 1
Продолжаем рассуждение.
Уменьшить число в 10 раз, значит число нужно разделить на 10.
Чтобы разделить число на 10, нужно убрать у него справа один нуль.
840 : 10 = 84
900 : 10 = 90
360 : 10 = 36
Оформляем задание в тетрадь.
8 ∙ 10 = 80
12 ∙ 10 = 120
35 ∙ 10 = 350
700 : 100 = 7
400 : 100 = 4
100 : 100 = 1
840 : 10 = 84
900 : 10 = 90
360 : 10 = 36
Номер 2.
На каждом этаже девятиэтажного дома по три квартиры. Номера квартир на седьмом этаже: 127, 128, 129. Назови номера трех квартир на следующем этаже; на предыдущем этаже.
Ответ:На следующем этаже: 130, 131, 132. На предыдущем этаже: 124, 125, 126.
1) Вспомни, как получается каждое следующее число при счете.
2) Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Последняя квартира на 7 этаже имеет № 129.
Значит, чтобы узнать номер следующей квартиры, нужно к числу 129 прибавить 1. На 8 этаже таких квартир три.
129 + 1 = 130
130 + 1 = 131
131 + 1 = 132
Продолжаем рассуждение.
Первая квартира на 7 этаже имеет №127.
Значит, чтобы узнать номер предыдущей квартиры, нужно из числа 127 вычесть 1. На 6 этаже также три квартиры.
127 – 1 = 126
126 – 1 = 125
125 – 1 = 124
Оформляем задание в тетрадь.
На следующем этаже: 130, 131, 132.
На предыдущем этаже: 124, 125, 126.
Номер 3.
В лыжной эстафете участвовали 9 команд мальчиков, по 8 человек в каждой, и еще 24 девочки. Во сколько раз больше мальчиков, чем девочек, участвовало в эстафете?
Измени вопрос, чтобы последним действием при решении было вычитание. Реши новую задачу.

1) «Во сколько раз больше» – вычисляется делением;
2) «На сколько больше» – вычисляется вычитанием.
Оформляем краткую запись.
-(2024).jpg)
Рассуждаем.
9 команд по 8 человек, это значит, что в каждой команде 8 человек и таких команд 9. Сложение одинаковых слагаемых, можно заменить умножением.
9 ∙ 8 = 72 (м.) – всего участвовало.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
72 : 24 = 3 (раза) – во столько раз больше мальчиков, чем девочек.
Записываем ответ.
Ответ: в 3 раза больше мальчиков, чем девочек.
Оформляем краткую запись.
На сколько больше мальчиков, чем девочек, участвовало в эстафете.
-(2024).jpg)
Рассуждаем.
В предыдущей задаче мы уже узнали, что в эстафете участвовало 72 мальчика.
Теперь, чтобы узнать, на сколько больше мальчиков, чем девочек, участвовало в эстафете, нужно из количества мальчиков вычесть количество девочек.
72 – 24 = 48 (чел.) – на сколько больше мальчиков, чем девочек.
Записываем ответ.
Ответ: на 48 человек больше мальчиков, чем девочек, участвовало в эстафете.
Номер 4.
Ответ:1 м = 10 дм 1 дм = 10 см 1 м > 10 см 1 дм > 10 мм 1 дм2 > 10 см2 1 см2 = 100 мм2
1) Помни, что:
1 м = 10 дм = 100 см;
1 см2 = 100 мм2;
1 см2 = 100 см2.
2) Помни, что сравнивать числовые значения длины можно только, если они выражены в одних единицах измерения.
Рассуждаем.
Сравним 1 м и 10 дм.
Переведем 1 м в дециметры:
1 м = 10 дм
10 дм = 10 дм, значит:
1 м = 10 дм.
Сравним 1 м и 10 см
Переведем 1 м в сантиметры:
1 м = 100 см
100 см > 10 см, значит:
1 м > 10 см.
Сравним 1 дм2 и 10 см2.
Переведем 1 дм2 в сантиметры квадратные:
1 дм2 = 10 см ∙ 10 см = 100 см2
100 см2 > 10 см2, значит:
1 дм2 > 10 см2
Сравним 1 дм и 10 см
Переведем 1 дм в сантиметры:
1 дм = 10 см
10 см = 10 см, значит:
1 дм = 10 см.
Сравним 1 дм и 10 мм
Переведем 1 дм в миллиметры:
1 дм = 10 см = 100 мм
100 мм > 10 мм, значит:
1 дм > 10 мм.
Сравним 1 см2 и 100 мм2.
Переведем 1 см2 в миллиметры квадратные:
1 см2 = 10 мм ∙ 10 мм = 100 мм2
100 мм2 = 100 мм2, значит:
1 см2 = 100 мм2.
Оформляем задание в тетрадь.
1 м = 10 дм
1 м > 10 см
1 дм2 > 10 см2
1 дм = 10 см
1 дм > 10 мм
1 см2 = 100 мм2
Номер 5.
Реши уравнения и сделай проверку.
Ответ:х : 3 = 17
х = 17 · 3
х = 51
Ответ: 51
Проверка:
51 : 3 = 17
17 = 17
Ответ: х = 51
49 – х = 28
х = 49 – 28
х = 21
Ответ: 21
Проверка:
49 – 21 = 28
28 = 28
Ответ: х = 21
64 : х = 4
х = 64 : 4
х = 16
Ответ: 16
Проверка:
64 : 16 = 4
4 = 4
Ответ: х = 16
Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
х : 3 = 17
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
х = 17 ∙ 3
17 ∙ 3 = (10 + 7) ∙ 3 = 30 + 21 = 51
х = 51
49 – х = 28
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 49 − 28
х = 21
64 : х = 4
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 64 : 4
64 : 4 = (40 + 24) : 4 = 10 + 6 = 16
х = 16
Сделаем проверку.
х : 3 = 17
Проверка: вместо неизвестного подставим число 51
51 : 3 = (30 + 21) : 3 = 10 + 7 = 17
17 = 17
49 – х = 28
Проверка: вместо неизвестного подставим число 21.
49 – 21 = 28
28 = 28
64 : х = 4
Проверка: вместо неизвестного подставим число 16.
64 : 16 = 4
4 = 4
Оформляем задание в тетрадь.
х : 3 = 17
х = 17 ∙ 3
х = 51
Проверка:
51 : 3 = 17
17 = 17
49 – х = 28
х = 49 − 28
х = 21
Проверка:
49 – 21 = 28
28 = 28
64 : х = 4
х = 64 : 4
х = 16
Проверка:
64 : 16 = 4
4 = 4
Номер 6.
Ответ:
1) Вспомни, как выполнить деление с остатком.
2) Помни о порядке выполнения арифметических действий.
3) Сначала выполняются действия умножение или деление, а потом – сложение или вычитание. Слева направо.
Выполняем вычисления.
28 + 42 : 7 – 6 = 28
1) 42 : 7 = 6
2) 28 + 6 = 34
3) 34 – 6 = 28
96 – 72 : 9 + 15 = 103
1) 72 : 9 = 8
2) 96 – 8 = 88
3) 88 + 15 = 103
32 + 56 : 8 – 7 = 32
1) 56 : 8 = 7
2) 32 + 7 = 39
3) 39 – 7 = 32
100 – 7 ∙ 8 = 44
1) 7 ∙ 8 = 56
2) 100 – 56 = 44
90 – 8 ∙ 8 = 26
1) 8 ∙ 8 = 64
2) 90 – 64 = 26
80 – 9 ∙ 8 = 8
1) 9 ∙ 8 = 72
2) 80 – 72 = 8
74 : □ = 8 (ост. □)
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
74 не делится на 8 без остатка. Вспомним, какое самое большое число до 74 делится на 8 без остатка. Это 72.
Найдём частное: 72 : 8 = 9.
Найдём остаток: 74 – 72 = 2.
Значит, 74 : 9 = 8 (ост. 2)
65 : □ = 7 (ост. □)
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
65 не делится на 7 без остатка. Вспомним, какое самое большое число до 65 делится на 7 без остатка. Это 63.
Найдём частное: 63 : 7 = 9.
Найдём остаток: 65 – 63 = 2.
Значит, 65 : 9 = 7 (ост. 2)
85 : □ = 9 (ост. □)
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
85 не делится на 9 без остатка. Вспомним, какое самое большое число до 85 делится на 9 без остатка. Это 81.
Найдём частное: 81 : 9 = 9.
Найдём остаток: 85 – 81 = 4.
Значит, 85 : 9 = 9 (ост. 4)
Оформляем задание в тетрадь.
28 + 42 : 7 – 6 = 28 + 6 – 6 = 34 – 6 = 28
96 – 72 : 9 + 15 = 96 – 8 + 15 = 88 + 15 = 103
32 + 56 : 8 – 7 = 32 + 7 – 7 = 39 – 7 = 32
100 – 7 ∙ 8 = 100 – 56 = 44
90 – 8 ∙ 8 = 90 – 64 = 26
80 – 9 ∙ 8 = 80 – 72 = 8
74 : 9 = 8 (ост. 2)
65 : 9 = 7 (ост. 2)
85 : 9 = 9 (ост. 4)
Номер 7.
1) По какому правилу составлены ряды из фигур? 2) Составь все возможные трехзначные числа, используя цифры 2, 7, 5 и не повторяя одну и ту же цифру в записи одного числа.

Ряды из фигур составлены так, что местами меняют фигуры. Сначала на первое место ставят на двух картинках красный круг, а за тем переставляют квадрат и треугольник. На 3 и 4 рисунках на первом месте стоит синий треугольник, а квадрат и круг меняются местами. Аналогично на 5 и 6 картинках, зелёный квадрат на первом месте, а круг и треугольник меняются местами. Фигуры не повторяются и меняются местами. 2) 2, 7, 5 275, 257 725, 752 572, 527
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Рассмотрим ряды фигур.
Ряды фигур составлены так, что фигуры меняют местами без повторений.
Рассмотрим 1 и 2 ряд.
Сначала на первое место ставят красный круг, а квадрат и треугольник меняют местами.
Рассмотрим 3 и 4 ряды.
На первое место теперь ставят треугольник, а квадрат и круг меняют местами.
Рассмотрим 5 и 6 ряды.
На первое место ставят квадрат, а круг и треугольник меняют местами.
Продолжаем рассуждение.
С помощью фигур показано, как можно составить всевозможные трёхзначные числа, не повторяя одну и ту же цифру в записи одного числа.
Подобным образом, составим трёхзначные числа из цифр 2, 5 и 7.
257, 275, 527, 572, 725, 752.
Задание вверху страницы
Запиши число 3. Припиши к нему справа цифру 0. На каком месте теперь стоит цифра 3 и что она означает? Во сколько раз 3 десятка больше, чем 3 единицы? Сравни так же 9, 90 и 900. Как изменится число 200, если в его записи справа отбросить 1 нуль? 2 нуля?
Ответ:3 – 3 единицы
30 – 3 десятка, 0 единиц
30 : 3 = 10 (раз) – во столько раз 3 десятка больше, чем 3 единицы
90 : 9 = 10 (раз) – во столько раз 90 больше 9
900 : 9 = 100 (раз) – во столько раз 900 больше 9
900 : 90 = 10 (раз) – во столько раз 900 больше 90
200
20 – уменьшится в 10 раз
2 – уменьшится в 100 раз
Рассуждая, узнаем, как можно получить число, которое больше или меньше данного в 10 раз; в 100 раз.
Рассуждаем.
Если к числу 3 справа приписать цифру 0, то получится число 30.
3 стоит в десятках, 0 – в единицах.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
30 : 3 = 10 (раз) – во столько раз 3 десятка больше, чем 3 единицы.
Продолжаем рассуждение.
Сравним числа.
90 : 9 = 10 (раз) – во столько раз 90 больше 9.
900 : 9 = 100 (раз) – во столько раз 900 больше 9.
900 : 90 = 10 (раз) – во столько раз 900 больше 90.
Продолжаем рассуждение.
Если у числа 200 отбросить справа 1 нуль, то получится число 20. Значит, число уменьшится в 10 раз.
200 : 20 = 20 дес. : 2 дес. = 10
Если у числа 200 отбросить справа 2 нуля, то получится число 2. Значит, число уменьшиться в 100 раз.
200 : 2 = 2 сот. : 2 = 1 сот. = 100
Задание внизу страницы
Уменьши в 100 раз числа: 600, 200, 800.
Ответ:6, 2, 8.
Повтори, как можно получить число, которое больше или меньше данного в 100 раз.
Рассуждаем.
Уменьшить число в 100 раз, значит, число нужно разделить на 100.
Чтобы разделить число на 100, нужно убрать у него справа два нуля.
Оформляем задание в тетрадь.
600 : 100 = 6
200 : 100 = 2
800 : 100 = 8
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.