Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 23

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 2.
Выбери все высказывания, верные для этого рисунка.
1) Если фигура не синего цвета, то это прямоугольник.
2) Если фигура не красного цвета, то это не прямоугольник.
3) Если фигура не треугольник, то она не синего цвета.
Закончи высказывание, верное для данного рисунка:
Если фигура не желтого цвета, то это не ... .

2), 3)
Если фигура не желтого цвета, то это не круг.
1) Доказывай все высказывания или опровергай их, подбирая обоснования или опровержения.
2) Помни, что фигуру называют по количество углов. Опиши сначала все, а потом узнаешь, какие высказывания верны, а какие – нет.
Рассмотрим фигуры.
Опишем все фигуры по из свойствам: количесвто углов, цвет, размер.
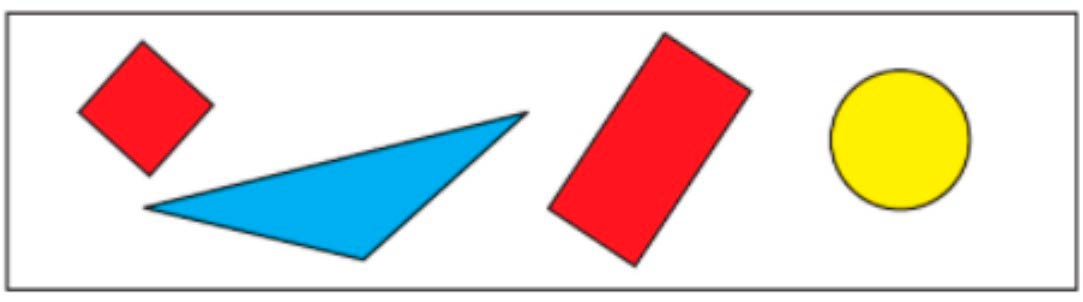
Фигура 1 – маленький красный квадрат;
Фигура 2 – большой синий треугольник;
Фигура 3 – большой красный прямоугольник;
Фигура 4 – жёлтый круг.
Рассмотрим высказывания.
1) Если фигура не синего цвета, то это прямоугольник – не верно, так как круг тоже не синего цвета.
2) Если фигура не красного цвета, то это не прямоугольник – верно, так как квадрат и прямоугольник только красного цвета, а квадрат – это тоже прямоугольник.
3) Если фигура не жёлтого цвета, то она не круг – верно, так как только круг жёлтого цвета.
Закончим высказывание:
Если фигура не желтого цвета, то это не круг.
Так как только круг жёлтого цвета.
Записываем ответ.
1) Если фигура не синего цвета, то это прямоугольник – не верно;
2) Если фигура не красного цвета, то это не прямоугольник – верно;
3) Если фигура не треугольник, то она не синего цвета – верно;
Если фигура не желтого цвета, то это не круг.
Номер 3.
Какое число будет получаться на выходе из машины, если в нее ввести число 5; 37; 62; 23; 66; 96?

5 → 8
37 → 72
62 → 38
23 → 44
66 → 40
96 → 55
Рассуждение:
5 четное? Нет, значит, 5 ∙ 2 – 2 = 10 – 2 = 8
37 четное? Нет, значит, 37 ∙ 2 – 2 = 74 – 2 = 72
62 четное? Да, значит, 62 : 2 + 7 = 31 + 7 = 38
23 четное? Нет, значит, 23 ∙ 2 – 2 = 46 – 2 = 44
66 четное? Да, значит, 66 : 2 + 7 = 33 + 7 = 40
96 четное? Да, значит, 96 : 2 + 7 = 48 + 7 = 55
1) Вычислительная машина – машина, производящая некоторые действия с числами.
2) Рассмотри вычислительную машину, какие действия выполняются с введенным числом.
Разберем, как работает машина.
1) В машину поступает число.
2) Если число чётное, то его делят на 2 и прибавляют к частному 7.
3) Если число нечетное, то его умножают на 2 и из произведения вычитают 2.
4) Получаем число на выходе.
Вычисляем по этапам.
Число 5.
1) В машину поступает число 5.
2) Число 5 – нечетное.
3) 5 ∙ 2 – 2 = 10 – 2 = 8
4) Получается число 8.
Число 37.
1) В машину поступает число 37.
2) Число 37 – нечётное.
3) 37 ∙ 2 – 2 = 74 – 2 = 72
4) Получаем число 72.
Число 62.
1) В машину поступает число 62.
2) Число 62 – чётное.
3) 62 : 2 + 7 = 31 + 7 = 38
4) Получаем число 38.
Число 23.
1) В машину поступает число 23.
2) Число 23 – нечётное.
3) 23 ∙ 2 – 2 = 46 – 2 = 44
4) Получаем число 44.
Число 66.
1) В машину поступает число 66.
2) Число 66 – чётное.
3) 66 6 2 + 7 = 33 + 7 = 40
4) Получаем число 40.
Число 96.
1) В машину поступает число 96.
2) Число 96 – чётное.
3) 96 : 2 + 7 = 48 + 7 = 55
4) Получаем число 55.
Оформляем задание в тетрадь.
Число 5 – Четное? НЕТ → 5 ∙ 2 – 2 = 10 – 2 = 8 →Выход: 8.
Число 37 – Четное? НЕТ → 37 ∙ 2 – 2 = 74 – 2 = 72 → Выход: 72.
Число 62 – Четное? ДА → 62 : 2 + 7 = 31 + 7 = 38 → Выход: 38.
Число 23 – Четное? НЕТ → 23 ∙ 2 – 2 = 46 – 2 = 44 → Выход: 44.
Число 66 – Четное? ДА → 66 : 2 + 7 = 33 + 7 = 40 → Выход: 40.
Число 96 – Четное? ДА → 96 : 2 + 7 = 48 + 7 = 55 → Выход: 55.
Номер 7.
Определи, как можно, не изменяя чисел, сделать равенства верными. Выполни это.
Ответ:Нужно поставить скобки.

1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем скобки и порядок действий.
1 2
(100 − 24) : 2 = 38
2 1
36 : (6 + 3) = 4
1 2 3
(48 − 20) : 4 · 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30
Делаем проверку и вычисляем по действиям.
1 2
(100 − 24) : 2 = 38
1) 100 – 24 = 76
2) 76 : 2 = (60 + 16) : 2 = 30 + 8 = 38
2 1
36 : (6 + 3) = 4
1) 6 + 3 = 9
2) 36 : 9 = 4
1 2 3
(48 − 20) : 4 · 5 = 35
1) 48 – 20 = 28
2) 28 : 4 = 7
3) 7 ∙ 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30
1) 5 ∙ 6 = 30
2) 30 : 30 = 1
3) 1 + 29 = 30
Оформляем задание в тетрадь.
1 2
(100 − 24) : 2 = 76 : 2 = 38
2 1
36 : (6 + 3) = 36 : 9 = 4
1 2 3
(48 − 20) : 4 · 5 = 28 : 4 · 5 = 7 · 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30 : 30 + 29 = 1 + 29 = 30
Номер 8.
Ответ:
1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним вычисления способом умножения или деления суммы на число.
32 ∙ 3 = (30 + 2) ∙ 3 = 30 ∙ 3 + 2 ∙ 3 = 90 + 6 = 96
Представим число 32 в виде суммы 30 и 2. Умножим каждое слагаемое на 3 и полученные результаты сложим.
62 : 2 = (60 + 2) : 2 = 60 : 2 + 2 : 2 = 30 + 1 = 31
Представим число 62 в виде суммы 60 и 2. Разделим каждое слагаемое на 2 и полученные результаты сложим.
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
Представим число 24 в виде суммы 20 и 4. Умножим каждое слагаемое на 3 и полученные результаты сложим.
Выполним вычисления по действиям.
(96 + 4) : 20 = 5
1) 96 + 4 = 100
2) 100 : 20 = 10 дес. : 2 дес. = 10 : 2 = 5
(31 – 7) : 24 = 1
1) 31 – 7 = 24
2) 24 : 24 = 1
72 : 8 ∙ 11 = 99
1) 72 : 8 = 9
2) 9 ∙ 11 = 9 ∙ (10 + 1) = 90 + 9 = 99
98 – 33 ∙ 2 = 32
1) 33 ∙ 2 = (30 + 3) ∙ 2 = 60 + 6 = 66
2) 98 – 66 = 32
100 – 2 ∙ 19 = 62
1) 2 ∙ 19 = 2 ∙ (10 + 9) = 20 + 18 = 38
2) 100 – 38 = 62
9 ∙ 9 + 17 = 98
1) 9 ∙ 9 = 81
2) 81 + 17 = 98
Оформляем задание в тетрадь.
32 ∙ 3 = (30 + 2) ∙ 3 = 30 ∙ 3 + 2 ∙ 3 = 90 + 6 = 96
62 : 2 = (60 + 2) : 2 = 60 : 2 + 2 : 2 = 30 + 1 = 31
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
(96 + 4) : 20 = 100 : 20 = 5
(31 – 7) : 24 = 24 : 24 = 1
72 : 8 ∙ 11 = 9 ∙ 11 = 99
98 – 33 ∙ 2 = 98 – 66 = 32
100 – 2 ∙ 19 = 100 – 38 = 62
9 ∙ 9 + 17 = 81 + 17 = 98
Номер 9.
Ответ:

1) a · b, значит, значение a нужно умножить на b.
2) c : d, значит, значение c нужно разделить на d.
Рассуждаем.
Таблица 1.
a ∙ b, если:
а = 23, b = 3, то 23 ∙ 3 = (20 + 3) ∙ 3 = 20 ∙ 3 + 3 ∙ 3 = 60 + 9 = 69
а = 24, b = 3, то 24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
а = 25, b = 3, то 25 ∙ 3 = (20 + 5) ∙ 3 = 20 ∙ 3 + 5 ∙ 3 = 60 + 15 = 75
а = 26, b = 3, то 23 ∙ 3 = (20 + 6) ∙ 3 = 20 ∙ 3 + 6 ∙ 3 = 60 + 18 = 78
При вычислении выражений используем правило умножения суммы на число.
Таблица 2.
с : d, если:
с = 72, d = 2, то 72 : 2 = (60 + 12) : 2 = 60 : 2 + 12 : 2 = 30 + 6 = 36
с = 72, d = 3, то 72 : 3 = (60 + 12) : 3 = 60 : 3 + 12 : 3 = 20 + 4 = 24
с = 72, d = 4, то 72 : 4 = (40 + 32) : 4 = 40 : 4 + 32 : 4 = 10 + 8 = 18
с = 72, d = 6, то 72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12
При вычислении выражений используем правило деления суммы на число.
Заполним таблицы.
.jpg)
Номер 10.
Для изготовления 5 одинаковых скворечников потребовалось заготовить 20 прямоугольных и 10 квадратных дощечек. Сколько всего дощечек идет на 1 скворечник?
5 скв. – 20 и 10 д. 1 скв. – ? д. 1) 20 + 10 = 30 (д.) – на 5 скворечников. 2) 30 : 5 = 6 (д.) – на один скворечник. Ответ: 6 дощечек идёт на 1 скворечник. Или 1) 20 : 5 = 4 (шт.) – прямоугольных дощечек потребовалось. 2) 10 : 5 = 2 (шт.) – квадратных дощечек потребовались. 3) 2 + 4 = 6 (д.) – потребовалось всего. Ответ: 6 дощечек идёт на 1 скворечник.
Решение задачи сводится к применению правила деления суммы на число:
1) Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число;
2) Чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Оформляем краткую запись.
5 сквор. – 20 пр. д. и 10 кв. д.
1 сквор. – ? д.
Рассуждаем.
Узнаем, сколько всего дощечек понадобилось для 5 одинаковых скворечников. Общее количество дощечек складывается из прямоугольных и квадратных дощечек.
20 + 10 = 30 (д.) – всего понадобилось для 5 скворечников.
Продолжаем рассуждение.
Узнаем, сколько дощечек понадобится для 1 скворечника. Мы теперь знаем, что для 5 скворечников понадобилось 30 дощечек. При чём все скворечники одинаковые. Значит, чтобы найти сколько дощечек необходимо для 1 скворечника, нужно общее количество дощечек разделить на количество скворечников.
30 : 5 = 6 (д.) – нужно для 1 скворечника.
Записываем ответ.
Ответ: 6 дощечек идёт на один скворечник.
Решение выражением: (20 + 10) : 5 = 6 (шт.) – дощечек для 1 скворечника, где 20 + 10 – количество дощечек для 5 скворечников.
Рассуждаем.
Узнаем, сколько по отдельности прямоугольных и квадратных дощечек понадобится для одного скворечника. Все скворечники одинаковые. Значит, чтобы найти сколько отдельно дощечек каждого вида необходимо для 1 скворечника, нужно общее количество дощечек каждого вида разделить на количество скворечников.
20 : 5 = 4 (д.) – прямоугольных понадобится для 1 скворечника.
10 : 5 = 2 (д.) – квадратных понадобится для 1 скворечника.
Продолжаем рассуждение.
Узнаем, сколько всего дощечек нужно для 1 скворечника. Общее количество дощечек для 1 скворечника складывается из прямоугольных и квадратных дощечек – это вычисляется сложением.
4 + 2 = 6 (д.) – нужно для 1 скворечника.
Записываем ответ.
Ответ: 6 дощечек идёт на один скворечник.
Решение выражением: 20 : 5 + 10 : 5 = 6 (шт.) – дощечек для 1 скворечника, где 20 : 5 – прямоугольных дощечек; 10 : 5 – квадратных дощечек.
Номер 11.
Дети играли в слова. Маша составила 9 слов, а Слава – 27 других слов. Во сколько раз больше слов составил Слава, чем Маша? На сколько у Славы больше слов, чем у Маши?
Ответ:
1) 27 : 9 = 3 (р.)– во столько слов больше у Славы. 2) 27 – 9 = 18 (сл.)– на столько больше у Славы. Ответ: в 3 раза больше, на 18 слов больше.
1) «во сколько раз больше» – вычисляется делением;
2) «на сколько больше», – вычисляется вычитанием.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз больше Слава составил слов, чем Маша, нужно количество Славиных слов разделить на количество Машиных слов.
27 : 9 = 3 (р.) – во столько больше у Славы, чем у Маши.
Продолжаем рассуждение.
Чтобы узнать, на сколько больше слов составил Слава, чем Маша, нужно из количества Славиных слов вычесть количество Машиных.
27 – 9 = 18 – на столько больше у Славы, чем у Маши.
Записываем ответ.
Ответ: в 3 раза больше, на 18 слов больше.
Номер 12.
Ответ:1)
.jpg)
2) 0 : 8 = 0 17 ∙ 1 = 17 24 : 1 = 24 0 ∙ 8 = 0 17 + 0 = 17 24 – 0 = 24
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Расставляем порядок действий и выполняем вычисления.
1) Выполним вычисления способом деления суммы на число.
36 : 3 = (30 + 6) : 3 = 30 : 3 + 6 : 3 = 10 + 2 = 12
Число 36 представим в виде суммы 30 и 6. Каждое слагаемое разделим на 3 и полученные результаты сложим.
82 : 2 = (80 + 2) : 2 = 80 : 2 + 2 : 2 = 40 + 1 = 41
Число 82 представим в виде суммы 80 и 2. Каждое слагаемое разделим на 2 и полученные результаты сложим.
42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
Число 42 представим в виде суммы 30 и 12. Каждое слагаемое разделим на 3 и полученные результаты сложим.
78 : 6 = (60 + 18) : 6 = 60 : 6 + 18 : 6 = 10 + 3 = 13
Число 78 представим в виде суммы 60 и 18. Каждое слагаемое разделим на 6 и полученные результаты сложим.
30 : 2 = (20 + 10) : 2 = 20 : 2 + 10 : 2 = 10 + 5 = 15
Число 30 представим в виде суммы 20 и 10. Каждое слагаемое разделим на 2 и полученные результаты сложим.
74 : 2 = (60 + 14) : 2 = 60 : 2 + 14 : 2 = 30 + 7 = 37
Число 74 представим в виде суммы 60 и 14. Каждое слагаемое разделим на 2 и полученные результаты сложим.
Выполним вычисления по действиям.
65 – 64 : 8 ∙ 3 = 41
1) 64 : 8 = 8
2) 8 ∙ 3 = 24
3) 65 – 24 = 41
9 ∙ (14 – 9) – 8 = 37
1) 14 – 9 = 5
2) 9 ∙ 5 = 45
3) 45 – 8 = 37
2) Найдём значение неизвестного с помощью рассуждений.
: 8 = 0
Если частное равно 0, значит, и делимое тоже равняется 0.
0 : 8 = 0
Ответ: 0.
∙ 8 = 0
Если произведение равно 0, значит, один из множителей тоже равен 0.
0 ∙ 8 = 0
Ответ: 0.
17 ∙ = 17
Число не изменится, если умножить его на 1.
17 ∙ 1 = 17
Ответ: 1.
17 + = 17
Число не изменится, если к нему прибавить 0.
17 + 0 = 17
Ответ: 0.
24 : = 24
Число не изменится, если его разделить на 1.
24 : 1 = 24
Ответ: 1.
24 – = 24
Число не изменится, если из него вычесть 0.
24 – 0 = 24
Ответ: 0.
Оформляем задание в тетрадь.
1)
36 : 3 = (30 + 6) : 3 = 10 + 2 = 12
82 : 2 = (80 + 2) : 2 = 40 + 1 = 41
42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
30 : 2 = (20 + 10) : 2 = 10 + 5 = 15
74 : 2 = (60 + 14) : 2 = 30 + 7 = 37
65 – 64 : 8 ∙ 3 = 65 – 8 ∙ 3 = 65 – 24 = 41
9 ∙ (14 – 9) – 8 = 9 ∙ 5 – 8 = 45 – 8 = 37
2)
0 : 8 = 0
0 ∙ 8 = 0
17 ∙ 1 = 17
17 + 0 = 17
24 : 1 = 24
24 – 0 = 24
Номер 13.
Определи без измерений, где чей прямоугольник, если Витя начертил прямоугольник, площадь которого на 2 см2 меньше, чем площадь прямоугольника у Кости, но в 2 раза больше, чем площадь прямоугольника у Севы.

Синий прямоугольник Костин, красный прямоугольник Севы, зеленый прямоугольник Вити.
Площадь – часть плоскости, которую занимает фигура.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Рассмотрим прямоугольники.
Синий прямоугольник больше, чем зеленый прямоугольник и больше, чем розовый. Зелёный прямоугольник больше, чем розовый.
Расставим прямоугольники по возрастанию площади: розовый, зеленый, синий.
Продолжаем рассуждение.
У Вити прямоугольник меньше по площади, чем у Кости на 2 , значит у Кости площадь прямоугольника больше, чем у Вити.
У Вити прямоугольник по площади больше, чем у Севы в 2 раза.
Значит, у Кости большой прямоугольник, у Вити – средний, а у Севы – маленький.
Делаем вывод.
Костя начертил синий прямоугольник,
Витя начертил зеленый прямоугольник,
Сева начертил розовый прямоугольник.
Задание на полях страницы
Ребусы:



Вспомни названия компонентов действия сложения и вычитанием, умножения и деления, а также – зависимость между компонентами и результатами действий.
Рассуждаем.
Количетво единиц второго слагаемого неизвестно. Но чтобы узнать количество единиц второго слагаемого, нужно из единиц значения суммы вычесть количество единиц первого слагаемого.
Из 4 ед. мы не можем вычесть 8 ед., значит занимаем 1 дес. = 10 ед.,
10 + 4 = 14 ед.
14 ед. – 8 ед. = 6 ед.
Значит, во втором слагаемом 6 единиц.
Продолжаем рассуждение.
Количество десяток в первом слагаемом неизвестно. Но чтобы узнать чему равно количество десятков первого слагаемого, нужно из количества десятков значения суммы вычесть количесвто десятков второго слагаемого.
5 дес. – 2 дес. = 3 дес. и ещё 1 дес. занимали, осталось 3 дес. – 1 дес. = 2 дес.
Значит, в первом слагаемом 2 десятка.
Получим равенство:
28 + 26 = 54
Рассуждаем.
Количество единиц уменьшаемого неизвестно. Но количество единиц уменьшаемого можно узнать, если сложить количество единиц вычитаемого и разности.
Тогда, 2 ед. + 8 ед. = 10 ед – это 1 дес. 0 ед.
Значит, в уменьшаемом 0 единицы.
Продолжаем рассуждение.
Количество десятков вычитаемого неизвестно. Но количество десятков вычитаемого можно узнать, если из количества десятков уменьшаемого вычесть количество десятков значения разности.
7 дес. – 1 дес. = 6 дес. и ещё 1 дес. занимали, осталось 6 дес. – 1 дес. = 5 дес.
Значит, в вычитаемом 5 десятков.
Получим равенство:
70 – 52 = 18
Рассуждаем.
3 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 1.
4 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 6.
5 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 4.
Рассмотрим возможные варианты.
3 ребус. Возможные варианты:
3 ∙ 7 = 21
7 ∙ 3 = 21
9 ∙ 9 = 81
4 ребус. Возможные варианты.
2 ∙ 8 = 16
8 ∙ 2 = 16
4 ∙ 4 = 16
6 ∙ 6 = 36
4 ∙ 9 = 36
9 ∙ 4 = 36
7 ∙ 8 = 56
8 ∙ 7 = 56
5 ребус. Возможные варианты.
2 ∙ 7 = 14
7 ∙ 2 = 14
3 ∙ 8 = 24
8 ∙ 3 = 24
4 ∙ 6 = 24
6 ∙ 4 = 24
9 ∙ 6 = 54
6 ∙ 9 = 54
8 ∙ 8 = 64
Запишем ответ.
Представим несколько вариантов решения.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.