Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 102

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 25.
Ответ:250 + 250 ∙ 2 = 250 ∙ 3 = 750
(250 + 250) ∙ 2 = 500 ∙ 2 = 1000
(480 + 120) : 3 = 600 : 3 = 200
60 + 90 : 10 ∙ 3 = 60 + 9 ∙ 3 = 60 + 27 = 87
60 + 90 : (10 ∙ 3) = 60 + 90 : 30 = 60 + 3 = 63
120 – 80 : 4 ∙ 5 = 120 - 20 ∙ 5 = 120 - 100 = 20
84 – 24 + 48 : 6 = 60 + 8 = 68
84 − (24 + 48) : 6 = 84 - 72 : 6 = 84 - 12 = 72
100 – 64 + 36 : 4 = 100 - 64 + 9 = 36 + 9 = 45
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем и выполняем вычисления.
2 1
250 + 250 · 2 = 750
Первым действием выполняем умножение, а потом – сложение.
1) 250 ∙ 2 = (200 + 50) ∙ 2 = 400 + 100 = 500
2) 250 + 500 = (200 + 500) + 50 = 750
1 2
(250 + 250) ∙ 2 = 1000
Первым действием выполняем сложение в скобках, а потом – умножение.
1) 250 + 250 = (200 + 200) + (50 + 50) = 400 + 100 = 500
2) 500 ∙ 2 = 5 сот. ∙ 2 = 10 сот. = 1000
1 2
(480 + 120) : 3 = 200
Первым действием выполняем сложение в скобках, а потом - деление.
1) 480 + 120 = (400 + 100) + (80 + 20) = 500 + 100 = 600
2) 600 : 3 = 6 сот. : 3 = 2 сот. = 200
3 1 2
60 + 90 : 10 ∙ 3 = 87
Первым действием выполняем деление, потом – умножение и последним – сложение.
1) 90 : 10 = 9 дес. : 1 дес. = 9
2) 9 ∙ 3 = 27
3) 60 + 27 = 87
3 2 1
60 + 90 : (10 ∙ 3) = 63
Первым действием выполняем умножение в скобках, потом – деление и последним – сложение.
1) 10 ∙ 3 = 30
2) 90 : 30 = 3
3) 60 + 3 = 63
3 1 2
120 − 80 : 4 ∙ 5 = 20
Первым действием выполняем деление, потом – умножение и последним – вычитание.
1) 80 : 4 = 8 дес. : 4 = 2 дес. = 20
2) 20 ∙ 5 = 2 дес. ∙ 5 = 10 дес. = 100
3) 120 − 100 = (100 − 100) + 20 = 20
2 3 1
84 − 24 + 48 : 6 = 68
Первым действием выполняем деление, потом – вычитание и последним – сложение.
1) 48 : 6 = 8
2) 84 − 24 = (80 − 20) + (4 − 4) = 60
3) 60 + 8 = 68
3 1 2
84 − (24 + 48) : 6 = 72
Первым действием выполняем сложение в скобках, потом – деление и последним – вычитание.
1) 24 + 48 = (20 + 40) + (4 + 8) = 60 + 12 = 72
2) 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12
3) 84 − 12 = (80 − 10) + (4 − 2) = 70 + 2 = 72
2 3 1
100 − 64 + 36 : 4 = 45
Первым действием выполняем – деление, потом – вычитание и последним - сложение.
1) 36 : 4 = 9
2) 100 – 64 = 36
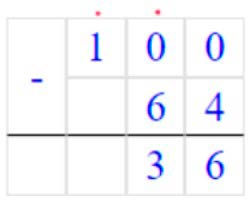
3) 36 + 9 = 36 + (4 + 5) = (36 + 4) + 5 = 40 + 5 = 45
Оформляем задание в тетрадь.
2 1
250 + 250 · 2 = 250 + 500 = 750
1 2
(250 + 250) ∙ 2 = 500 ∙ 2 = 1000
1 2
(480 + 120) : 3 = 600 : 3 = 200
3 1 2
60 + 90 : 10 ∙ 3 = 60 + 9 ∙ 3 = 60 + 27 = 87
3 2 1
60 + 90 : (10 ∙ 3) = 60 + 90 : 30 = 60 + 3 = 63
3 1 2
120 − 80 : 4 ∙ 5 = 120 − 20 ∙ 5 = 120 − 100 = 20
2 3 1
84 − 24 + 48 : 6 = 84 − 24 + 8 = 60 + 8 = 68
3 1 2
84 − (24 + 48) : 6 = 84 − 72 : 6 = 84 − 12 = 72
2 3 1
100 − 64 + 36 : 4 = 100 − 64 + 9 = 36 + 9 = 45
Номер 26.
Реши уравнения устно.
Ответ:х – 48 = 0
х = 48
125 : х = 125
х = 1
х ∙ 59 = 59
х = 1
Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассмотрим уравнения и выполняем вычисления.
х – 48 = 0
х – неизвестное уменьшаемое.
Если разность равна 0, значит уменьшаемое и вычитаемое равны.
Значит, х = 48
125 : х = 125
х – неизвестный делитель.
Если разделить на 1, то значение не изменится.
Значит, х = 1
х ∙ 59 = 59
х – неизвестный множитель.
Если множить на 1, то значение не изменится.
Значит, х = 1
Оформим задание в тетрадь.
х – 48 = 0
х = 48
125 : х = 125
х = 1
х ∙ 59 = 59
х = 1
Номер 27.
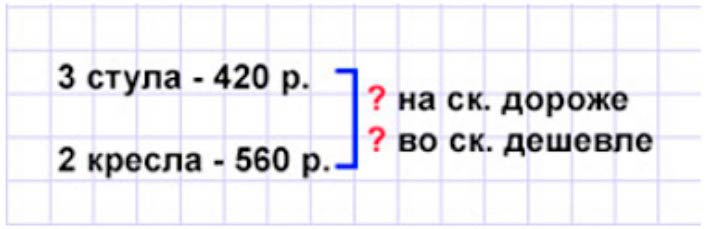
За 3 стула заплатили 420 р., а за 2 кресла − 560 р. На сколько рублей кресло дороже стула? Во сколько раз стул дешевле кресла?
Ответ:
1) 420 : 3 = 140 (р.) – цена одного стула. 2) 560 : 2 = 280 (р.) – цена одного кресла. 3) 280 − 140 = 140 (р.) – на столько дороже. 4) 280 : 140 = 2 (р.) – во столько раз дешевле. Ответ: на 140 рублей кресло дороже стула, в 2 раза стул дешевле кресла.
1) «На сколько дороже» – вычисляется разностью;
2) «Во сколько дешевле» – вычисляется делением.
Оформляем условие в виде краткой записи.
Рассуждаем.
Общая цена 3 стульев равна 420 рублей, а цена каждого стула одинакова. Значит, чтобы узнать стоимость 1 стула нужно общую стоимость разделить на количество стульев.
420 : 3 = (300 + 120) : 3 = 100 + 40 = 140 (р.) – цена 1 стула.
Продолжаем рассуждение.
Общая цена 2 кресел равна 560 рублей, а цена каждого кресла одинакова. Значит, чтобы узнать стоимость 1 кресла нужно общую стоимость разделить на количество кресел.
560 : 2 = (400 + 160) : 2 = 200 + 80 = 280 (р.) – цена 1 кресла.
Продолжаем рассуждение.
Дороже – это значит больше.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
280 − 140 = (200 – 100) + (80 – 40) = 100 + 40 = 140 (р.) – на столько дороже кресло, чем стул.
Продолжаем рассуждение.
Дешевле – это значит меньше.
Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
280 : 140 = 2 (р.) – во столько раз стул дешевле, чем кресло.
Записываем ответ.
Ответ: на 140 рублей; в 2 раза.
Номер 28.
Сравни уравнения каждой пары. Сравни их решения.
Ответ:х ∙ 4 = 160
х = 160 : 4
х = 40
х : 4 = 160
х = 160 ∙ 4
х = 640
В первом уравнении нужно найти неизвестное произведение, а для этого нужно произведение поделить на известный множитель.
Во втором уравнении нужно найти делимое, а для этого нужно делитель умножить на частное.
10 + х = 510
х = 510 ‒ 10
х = 500
10 ∙ х = 510
х = 510 : 10
х = 51
В первом примере нужно найти неизвестное слагаемое, а для этого нужно от суммы отнять второе слагаемое.
Во втором примере нужно найти неизвестный множитель, а для этого нужно произведение разделить на известный множитель.
80 : х = 5
х = 80 : 5
х = 16
80 ‒ х = 5
х = 80 ‒ 5
х = 75
В первом уравнении нужно найти неизвестный делитель, а для этого нужно делимое разделить на частное.
Во втором уравнении нужно найти вычитаемое, а для этого от уменьшаемого нужно отнять разность.
Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассмотрим уравнения.
х ∙ 4 = 160
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Вычисляется делением.
х : 4 = 160
х – неизвестное делимое.
Чтобы найти делимое нужно частное умножить на делимое.
Вычисляется умножением.
10 + х = 510
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
Вычисляется вычитанием.
10 ∙ х = 510
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Вычисляется делением.
80 : х = 5
х – делитель.
Чтобы найти делитель нужно делимое разделить на частное.
Вычисляется делением.
80 – х = 5
х – неизвестно вычитаемое.
Чтобы найти вычитаемое нужно из уменьшаемого вычесть разность.
Вычисляется вычитанием.
Решим уравнения.
х ∙ 4 = 160
х = 160 : 4
х = 40
х : 4 = 160
х = 160 ∙ 4 = (100 + 60) ∙ 4 = 400 + 240 = 640
х = 640
10 + х = 510
х = 510 – 10
х = 500
10 ∙ х = 510
х = 510 : 10
х = 51
80 : х = 5
х = 80 : 5 = (50 + 30) : 5 = 10 + 6 = 16
х = 16
х = 80 – 5
х = 79
Сравним уравнения.
Рассмотрим первую пару.
.jpg)
Рассмотрим вторую пару.
.jpg)
Рассмотрим третью пару.
.jpg)
Номер 29.
Запиши пропущенные наименования единиц измерения.
Ответ:1 кг = 1000 г
1 ч = 60 мин
1 м = 100 см
1 сут. = 24 ч
1 м = 10 дм
1 год = 12 мес
1) Повтори единицы длины и их зависимости - километр, метр, дециметр, сантиметр и миллиметр, единицы массы - тонну, центнер, килограмм и грамм.
2) Повтори единицы времени и их зависимости - год, месяц, сутки, час и минуту.
Рассмотрим измерения и заполним пропуски.
Рассмотрим первые измерения.
1 ... = 1000 ...
Одна величина в 1000 раз больше, другой величина – это может быть зависимость между килограммом и граммом или между километром и миллиметром.
1 кг = 1000 г
1 км = 1000 м
Рассмотрим вторые измерения.
1 ... = 60 ...
Одна величина в 60 раз больше, другой величины – это может быть зависимость между часом и минутой или между минутой и секундой.
1 ч = 60 мин
1 мин = 60 сек.
Рассмотрим третьи измерения.
1 ... = 100 ...
Одна величина в 100 раз больше, другой величины – это может быть зависимость между метром и сантиметром.
1 м = 100 см
Рассмотрим четвертые измерения.
1 ... = 24 ...
Одна величина в 24 раза больше другой величины – это может быть зависимость между сутками и часами.
1 сут. = 24 ч
Рассмотрим пятые измерения.
1 ... = 10 ...
Одна величина в 10 раз больше другой величины – это может быть зависимость между метром и дециметром; между дециметром и сантиметром; между сантиметром и миллиметром.
1 м = 10 дм или 1 дм = 10 см или 1 см = 10 мм
Рассмотрим шестые измерения.
1 ... = 12 ...
Она величина в 12 раз больше другой величины – это может быть зависимость между годом и месяцем.
1 год = 12 мес
Оформляем задание в тетрадь.
1 кг = 1000 г или 1 км = 1000 м.
1 ч = 60 мин или 1 мин = 60 сек.
1 м = 100 см.
1 сут. = 24 ч.
1 м = 10 дм или 1 дм = 10 см или 1 см = 10 мм.
1 год = 12 мес
Номер 30.
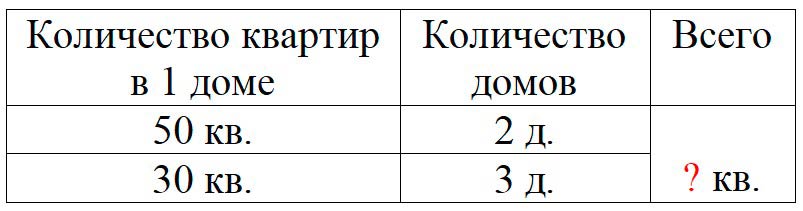
На улице построили 2 дома, по 50 квартир в каждом, и 3 дома, по 30 квартир в каждом. Сколько всего квартир в этих домах?
Ответ:Построили: 2 дома по 50 кв. 3 дома по 30 кв. Всего – ? кв. 1) 50 ∙ 2 = 100 (кв.) – в двух домах. 2) 30 ∙ 3 = 90 (кв.) – в 3 домах. 3) 100 + 90 = 190 (кв.) – всего в домах. Ответ: 190 квартир в этих домах всего.
Вспомни умножение на числа, оканчивающиеся нулем: чтобы умножить число на 10, нужно к нему справа приписать один нуль.
Оформляем условие в виде таблицы.
Рассуждаем.
Построили 2 дома и в каждом по 50 квартир. Значит, чтобы узнать общее количество квартир в этих двух домах нужно эти значения сложить, но сложение одинаковых слагаемых можно заменить умножение.
50 ∙ 2 = 100 (кв.) – в 2 домах.
Продолжаем рассуждение.
Построили 3 дома и в каждом по 30 квартир. Значит, чтобы узнать общее количество квартир в этих трех домах нужно эти значения сложить, но сложение одинаковых слагаемых можно заменить умножение.
30 ∙ 3 = 90 (кв.) – в 3 домах.
Продолжаем рассуждение.
В двух домах построили – 100 квартир, а в трех домах – 90 квартир.
Чтобы узнать общее число построенных квартир нужно эти данные сложить.
100 + 90 = 190 (кв.) – построили всего.
Записываем ответ.
Ответ: 190 квартир.
Решение выражением:
50 ∙ 2 + 30 ∙ 3 = 190 (кв.) – построили всего,
где 50 ∙ 2 – построили в 2 домах;
30 ∙ 3 – построили в 3 домах.
Номер 31.
Ответ:120 + 180 : 2 ∙ 5 = 120 + 90 * 5 = 120 + 450 = 570
120 + 180 : (2 ∙ 5) = 120 + 180 : 10 = 120 + 18 = 138
(120 + 180) : 2 ∙ 5 = 300 : 2 * 5 = 150 * 5 = 750
750 ‒ (150 ‒ 50) : 5 = 750 - 100 : 5 = 750 - 20 = 730
750 – 150 – 50 : 5 = 750 - 150 - 10 = 600 - 10 = 590
(750 – 150 ‒ 50) : 5 = (600 - 50) : 5 = 550 : 5 = 110
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем и выполняем вычисления.
3 1 2
120 + 180 : 2 · 5 = 570
Первым действием выполняем деление, потом – умножение и последним – сложение.
1) 180 : 2 = 18 дес. : 2 = 9 дес. = 90
2) 90 ∙ 5 = 9 дес. ∙ 5 = 45 дес. = 450
3) 120 + 450 = (100 + 400) + (20 + 50) = 500 + 70 = 570
3 2 1
120 + 180 : (2 ∙ 5) = 138
Первым действием выполняем умножение в скобках, потом – деление и последним – сложение.
1) 2 ∙ 5 = 10
2) 180 : 10 = 18
3) 120 + 18 = 100 + (20 + 18) = 100 + 38 = 138
1 2 3
(120 + 180) : 2 ∙ 5 = 750
Первым действием выполняем сложение в скобках, потом – деление и последним – умножение.
1) 120 + 180 = (100 + 100) + (20 + 80) = 200 + 100 = 300
2) 300 : 2 = (200 + 100) : 2 = 100 + 50 = 150
3) 150 ∙ 5 = (100 + 50) ∙ 5 = 500 + 250 = 750
3 1 2
750 − (150 − 50) : 5 = 730
Первым действием выполняем вычитание в скобках, потом – деление и последним – вычитание вне скобок.
1) 150 − 50 = 100
2) 100 : 5 = 10 дес. : 5 = 2 дес. = 20
3) 750 − 20 = 700 + (50 − 20) = 700 + 30 = 730
2 3 1
750 − 150 − 50 : 5 = 590
Первым действием выполняем деление, потом – вычитания по порядку слева направо.
1) 50 : 5 = 5 дес. : 5 = 1 дес. = 10
2) 750 − 150 = (700 − 100) + (50 - 50) = 600
3) 600 − 10 = 590
1 2 3
(750 − 150 − 50) : 5 = 110
Вначале выполняем вычитание в скобках по порядку слева направо, а потом деление.
1) 750 − 150 = (700 − 100) + (50 − 50) = 600
2) 600 − 50 = (500 + 100) − 50 = 500 + (100 − 50) = 500 + 50 = 550
3) 550 : 5 = 55 дес. : 5 = 11 дес. = 110
Оформляем задание в тетрадь.
3 1 2
120 + 180 : 2 · 5 = 120 + 90 · 5 = 120 + 450 = 570
3 2 1
120 + 180 : (2 ∙ 5) = 120 + 180 : 10 = 120 + 18 = 138
1 2 3
(120 + 180) : 2 ∙ 5 = 300 : 2 · 5 = 150 · 5 = 750
3 1 2
750 − (150 − 50) : 5 = 750 − 100 : 5 = 750 − 20 = 730
2 3 1
750 − 150 − 50 : 5 = 750 − 150 − 10 = 600 − 10 = 590
1 2 3
(750 − 150 − 50) : 5 = (600 − 50) : 5 = 550 : 5 = 110
Номер 32.
Поставь скобки, чтобы равенства стали верными:
Ответ:(100 − 24) : 2 = 38 (300 + 20) ∙ 3 : 10 = 96 360 : (6 + 3) = 40 420 : (10 − 4) : 2 = 35 32 ∙ (2 − 2) = 0 4 ∙ (120 − 120) : 6 = 0
1) Перебирай все возможные варианты, пытайся найти верное решение.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Расставим скобки и порядок действий.
1 2
(100 − 24) : 2 = 38
Первым действием выполним в скобках – вычитание, а вторым – деление.
2 1
360 : (6 + 3) = 40
Первым действием выполним в скобках – вычитание, а вторым – деление.
2 1
32 · (2 − 2) = 0
Первым действием выполним в скобках – вычитание, а вторым – деление.
1 2 3
(300 + 20) · 3 : 10 = 96
Первым действием выполним в скобках – сложение, вторым – умножение и последним – деление.
2 1 3
420 : (10 − 4) : 2 = 35
Первым действием выполним в скобках – вычитание, а вторым и третьим – деление.
2 1 3
4 · (120 − 120) : 6 = 0
Первым действием выполним в скобках – вычитание, вторым – умножение и последним – деление.
Выполним вычисления.
(100 − 24) : 2 = 38
1) 100 − 24 = 76
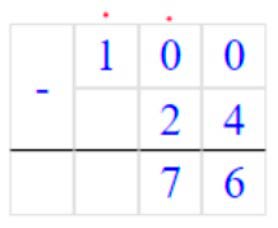
2) 76 : 2 = (60 + 16) : 2 = 30 + 8 = 38
360 : (6 + 3) = 40
1) 6 + 3 = 9
2) 360 : 9 = 36 дес. : 9 = 4 дес. = 40
32 ∙ (2 − 2) = 0
1) 2 − 2 = 0
2) 32 ∙ 0 = 0
(300 + 20) ∙ 3 : 10 = 96
1) 300 + 20 = 320
2) 320 ∙ 3 = (300 + 20) ∙ 3 = 900 + 60 = 960
3) 960 : 10 = 96
420 : (10 − 4) : 2 = 35
1) 10 − 4 = 6
2) 420 : 6 = 42 дес. : 6 = 7 дес. = 70
3) 70 : 2 = (60 + 10) : 2 = 30 + 5 = 35
4 ∙ (120 − 120) : 6 = 0
1) 120 − 120 = 0
2) 4 ∙ 0 = 0
3) 0 : 6 = 0
Оформим задание в тетрадь.
(100 − 24) : 2 = 76 : 2 = 38
360 : (6 + 3) = 360 : 9 = 40
32 ∙ (2 − 2) = 32 ∙ 0 = 0
(300 + 20) ∙ 3 : 10 = 320 ∙ 3 : 10 = 960 : 10 = 96
420 : (10 − 4) : 2 = 420 : 6 : 2 = 70 : 2 = 35
4 ∙ (120 − 120) : 6 = 4 ∙ 0 : 6 = 0
Номер 33.
Запиши названия прямоугольных, тупоугольных и остроугольных треугольников.

Прямоугольные треугольники: AKC, DCA, BCN, CKB, CKD. Тупоугольные треугольники: BCA, ANC, CBD, ACB. Остроугольные треугольники: ABC, CAB, NCA, CAN, KCA, CAK, ADC, CAD.
Вспомни как называются треугольник по видам углов:
Остроугольный треугольник – это тот треугольник у которого все углы меньше 90º;
Прямоугольный треугольник – это тот треугольник у которого один угол равен 90º;
Тупоугольный треугольник – это тот треугольник у которого один угол больше 90º.
Рассмотрим и характеризуем треугольники.
.jpg)
Треугольник СВD – тупоугольный, так как угол D > 90º.
.jpg)
Треугольник CKD – прямоугольный, так как угол К = 90º.
.jpg)
Треугольник СКN – прямоугольный, так как угол К = 90º.
.jpg)
Треугольник САN – тупоугольный, так как угол N больше 90º.
.jpg)
Треугольник СКВ – прямоугольный, так как угол К = 90º.
.jpg)
Треугольник СDN – остроугольный, так как все углы меньше 90º.
.jpg)
Треугольник СКА – прямоугольный, так как угол К = 90º.
.jpg)
Треугольник ВСN – острый, так как все углы меньше 90º.
.jpg)
Треугольник СВD – тупоугольный, так как угол С > 90º.
.jpg)
Треугольник АВС – тупоугольный, так как угол С > 90º.
Оформим задание в тетрадь.
CKB, CKD, CKN, CKA, ACD – прямоугольные треугольники.
ABC, CAN, CBD, CBA – тупоугольные треугольники.
BCN, CDN – остроугольные треугольники.
Задание на полях страницы
Сравни площади фигур:

Площади фигур одинаковы.
1) Чтобы вычислить площадь фигуры, нужно понять, какую часть плоскости она занимает в единицах квадратных единицах измерения.
2) Но у фигур сложных, т.е. у которых площадь нельзя вычислить по формуле, нужно поступать иначе. У сложных фигур площадь фигуры равна сумме площадей фигур, из которых она состоит.
Рассуждаем.
Рассмотрим первую фигуру.
Фигура состоит из 4 треугольников. Обозначим их цифрами.
Если треугольники 1 и 2 переместить, то получится прямоугольник со сторонами 2 см и 3 см (см. рисунок).
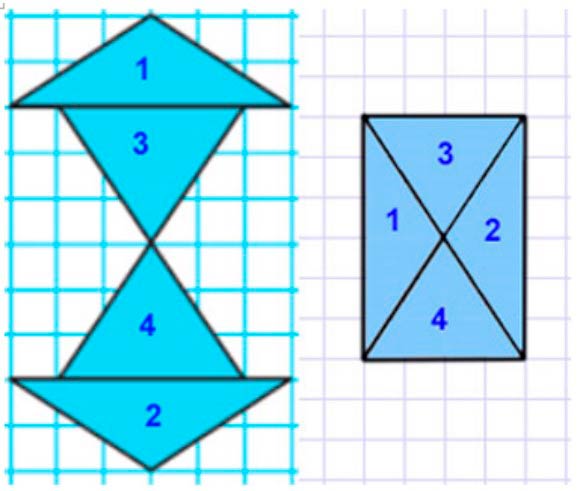
Вычислим площадь получившегося прямоугольника.
Площадь прямоугольника равна произведению его длины и ширины.
2 ∙ 3 = 6 см2 – площадь 1 фигуры.
Продолжаем рассуждение.
Рассмотрим вторую фигуру.
Вторая фигура — это прямоугольник со сторонами 3 см и 2 см.
3 ∙ 2 = 6 см2 – площадь 2 фигуры.
Делаем вывод.
Сравним площади фигур.
6 см2 = 6 см2 – площади фигур равны.
Значит, площадь фигуры 1 равна площади фигуры 2.
Ответ: площади равны.
Что узнали, чему научились в 3 классе?
Нумерация
Номер 1.
Назови число, следующее при счете за числом 99; 100; 299; 409; 1 000.
Ответ:100; 101; 300; 410; 1001.
1) Вспомни, как получается каждое следующее число при счете.
2) Вспомни, как образуются и называются трёхзначные числа.
Рассуждаем и выполняем вычисления.
Каждое следующее число при счете получается путем прибавления единицы к данному числу.
99 + 1 = 100
Значит, следующее число при счете за числом 99 – это число 100.
100 + 1 = 101
Значит, следующее число при счете за числом 100 – это число 101.
299 + 1 = 300
Значит, следующее число при счете за числом 299 – это число 300.
409 + 1 = 400 + (9 + 1) = 410
Значит, следующее число при счете за числом 409 – это число 410.
1000 + 1 = 1001
Значит, следующее число при счете за числом 1000 – это число 1001.
Делаем вывод:
99 → 100; 100 → 101; 299 → 300; 409 → 410; 1000 → 1001.
Записываем ответ.
Ответ: 100, 101, 300, 410 ,1001.
Номер 2.
Назови число, предшествующее при счете числам: 400, 350, 900, 891, 1 000.
Ответ:399, 349, 899, 890, 999.
1) Вспомни, как получается каждое предыдущее число при счете.
2) Вспомни, как образуются и называются трёхзначные числа.
Рассуждаем и выполняем вычисления.
Каждое предшествующее число образуется путем вычитания единицы из данного числа.
400 – 1 = 399
Значит, предыдущее при счете числу 400 – это число 399.
350 – 1 = 349
Значит, предыдущее при счете числу 350 – это число 349.
900 – 1 = 899
Значит, предыдущее при счете числу 900 – это число 899.
891 – 1 = 890
Значит, предыдущее при счете числу 891 – это число 890.
1000 – 1 = 999
Значит, предыдущее при счете числу 1000 – это число 999.
Делаем вывод:
400 → 399; 350 → 349; 900 → 899; 891 → 890; 1000 → 999.
Записываем ответ.
Ответ: 399, 349, 899, 890, 999.
Номер 3.
Что обозначает каждая цифра в записи чисел: 603, 637, 376, 608, 680, 600.
Ответ:603 – 6 сот. 0 дес. 3 ед. 637 – 6 сот. 3 дес. 7 ед. 376 – 3 сот. 7 дес. 6 ед. 608 – 6 сот. 0 дес. 8 ед. 680 – 6 сот. 8 дес. 0 ед. 600 – 6 сот. 0 дес. 0 ед.
1) Вспомни, как образуются и называются трёхзначные числа.
2) Вспомни, из чего состоит трёхзначное число;
3) Вспомни, что обозначает цифра 0 в числе.
Рассматриваем числа и рассуждаем.
Для записи трёхзначных чисел нужны три цифры – на первом месте стоят единицы, на втором – десятки и на третьем – сотни, начиная справа налево.
Рассмотрим число 603:
Число 6 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 3 обозначает единицы или единицы первого разряда.
Рассмотрим число 637:
Число 6 обозначает сотни или единицы третьего разряда.
Число 3 обозначает десятки или единицы второго разряда.
Число 7 обозначает единицы или единицы первого разряда.
Рассмотрим число 376:
Число 3 обозначает сотни или единицы третьего разряда.
Число 7 обозначает десятки или единицы второго разряда.
Число 6 обозначает единицы или единицы первого разряда.
Рассмотрим число 608:
Число 6 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 8 обозначает единицы или единицы первого разряда.
Рассмотрим число 680:
Число 6 обозначает сотни или единицы третьего разряда.
Число 8 обозначает десятки или единицы второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Рассмотрим число 600:
Число 6 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Оформляем задание в тетрадь.
603 = 6 сот. 0 дес. 3 ед.
637 = 6 сот. 3 дес. 7 ед.
376 = 3 сот. 7 дес. 6 ед.
608 = 6 сот. 0 дес. 8 ед.
680 = 6 сот. 8 дес. 0 ед.
600 = 6 сот. 0 дес. 0 ед.
Номер 4.
Запиши число, которое состоит из: 1) 3 сотен, 2 десятков, 5 единиц; 2) 9 сотен и 8 единиц; 3) 10 сотен.
Ответ:1) 325; 2) 908; 3) 1000.
1) Вспомни, как образуются и называются трёхзначные числа.
2) Вспомни, из чего состоит трёхзначное число;
3) Вспомни, что цифра обозначает отсутствие разряда в числе.
Рассмотрим числа и выполним вычисления.
Трехзначное число стоит из сотен, десяток и единиц.
На первом месте стоят единицы, на втором – десятки, на третьем – сотни, считая справа налево.
1) 3 сот. + 2 дес. + 5 ед. = 3 ∙ 100 + 2 ∙ 10 + 5 ∙ 1 = 300 + 20 + 5 = 325
2) 9 сот. + 8 ед. = 9 ∙ 100 + 8 ∙ 1 = 900 + 8 = 908
3) 10 сот. = 10 ∙ 100 = 1000
Оформим задание в тетрадь.
1) 325;
2) 908;
3) 1000.
Номер 5.
Сколько сотен, десятков и единиц в каждом числе: 807, 560, 347, 900?
Ответ:807 – 8 сот. 0 дес. 7 ед. 560 – 5 сот. 6 дес. 0 ед. 347 – 3 сот. 4 дес. 7 ед. 900 – 9 сот. 0 дес. 0 ед.
1) Вспомни, как образуются и называются трёхзначные числа.
2) Вспомни, из чего состоит трёхзначное число;
3) Вспомни, что обозначает цифра 0 в числе.
Рассуждаем.
Трехзначное число стоит из сотен, десяток и единиц. На первом месте стоят единицы, на втором – десятки, на третьем – сотни считая справа налево.
Число 807:
Число 8 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 7 обозначает единицы или единицы первого разряда.
Число 560:
Число 5 обозначает сотни или единицы третьего разряда.
Число 6 обозначает десятки или единицы второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Число 347:
Число 3 обозначает сотни или единицы третьего разряда.
Число 4 обозначает десятки или единицы второго разряда.
Число 7 обозначает единицы или единицы первого разряда.
Число 900:
Число 9 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Оформляем задание в тетрадь.
807 = 8 сот. 0 дес. 7 ед.
560 = 5 сот. 6 дес. 0 ед.
347 = 3 сот. 4 дес. 7 ед.
900 = 9 сот. 0 дес. 0 ед.
Номер 6.
Ответ:809 < 908 844 < 900 925 > 923 360 > 350 680 > 670 309 < 310
1) Вспомни, как образуются и называются трёхзначные числа.
2) Вспомни, как сравнивать числа.
Рассуждаем.
Сравним числа 809 и 908:
Сравним сотни: 8 сот. > 9 сот.
Значит, 809 > 908.
Сравним числа 360 и 350:
Сравним сотни: 3 сот. = 3 сот.
Сравним десятки: 6 дес. > 5 дес.
Значит, 360 > 350.
Сравним числа 844 и 900
Сравним сотни: 8 сот. < 9 сот.
Значит, 844 < 900.
Сравним числа 680 и 670
Сравним сотни: 6 сот. = 6 сот.
Сравним десятки: 8 дес. > 7 дес.
Значит, 680 > 670.
Сравним числа 925 и 923
Сравним сотни: 9 сот. = 9 сот.
Сравним десятки: 2 дес. = 2 дес.
Сравним единицы: 5 ед. > 3 ед.
Значит, 925 > 923.
Сравним числа 309 и 310
Сравним сотни: 3 сот. = 3 сот.
Сравним десятки: 0 дес. < 1 дес.
Значит, 309 < 310.
Оформляем задание в тетрадь.
809 < 908
360 > 350
844 < 900
680 > 670
925 > 923
309 < 310
Номер 7.
Запиши самое большое однозначное число и самое маленькое трехзначное число.
Ответ:Самое большое однозначное число: 9. Самое маленькое трёхзначное число: 100.
Вспомни, какие числа называются однозначными, а какие трёхзначными.
Рассуждаем.
Однозначное число – это число, которое состоит из одной цифры.
Это числа от 0 до 9.
Значит, 9 – самое большое однозначное число.
Продолжаем рассуждение.
Трехзначное число – это число, которое стоит из трех цифр, обозначающих сотни, десятки и единицы.
Это числа от 100 до 999.
Значит, 100 – самое маленькое трехзначное число.
Оформляем задание в тетрадь.
Самое большое однозначное число: 9.
Самое маленькое трёхзначное число: 100.
Номер 8.
Запиши каждое из следующих чисел в виде суммы разрядных слагаемых: 784, 608, 290, 304, 750, 809.
Ответ:784 = 700 + 80 + 4 608 = 600 + 8 290 = 200 + 90 304 = 300 + 4 750 = 700 + 50 809 = 800 + 9
1) Вспомни, как образуются и называются трёхзначные числа.
2) Вспомни, из чего состоит трёхзначное число;
3) Вспомни, что обозначает цифра 0 в числе.
4) Сумма разрядных слагаемых – это запись числа в виде сложения количества его разрядных единиц.
Рассуждаем.
Число 784:
Число 7 обозначает сотни или единицы третьего разряда.
Число 8 обозначает десятки или единицы второго разряда.
Число 4 обозначает единицы или единицы первого разряда.
Число 608:
Число 6 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 8 обозначает единицы или единицы первого разряда.
Число 290:
Число 2 обозначает сотни или единицы третьего разряда.
Число 9 обозначает десятки или единицы второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Число 304:
Число 3 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 4 обозначает единицы или единицы первого разряда.
Число 750:
Число 7 обозначает сотни или единицы третьего разряда.
Число 5 обозначает десятки или единицы второго разряда.
Число 0 обозначает отсутствие единиц или единиц первого разряда.
Число 809:
Число 8 обозначает сотни или единицы третьего разряда.
Число 0 обозначает отсутствие десятков или единиц второго разряда.
Число 9 обозначает единицы или единицы первого разряда.
.jpg)
Оформим задание в тетрадь.
784 = 700 + 80 + 4
608 = 600 + 8
290 = 200 + 90
304 = 300 + 4
750 = 700 + 50
809 = 800 + 9
Сложение и вычитание
Номер 1.
Объясни, почему верны равенства.
Ответ:Равенства равны, так как справа и слева одинаковые значения.
Используются следующие свойства:
1) а + b = b + a – переместительное свойство сложения.
2) (а + b) + c = a + (b + c) = (a + c) + b – сочетательное свойство сложения.
3) а + 0 = а и а – 0 = а – сложение и вычитание числа и 0.
Рассуждаем и выполняем вычисления.
76 + 345 = 345 + 76 – от перестановки слагаемых сумма не изменится.
Проверка:
76 + 345 = 300 + 70 + 40 + 6 + 5 = 300 + 110 + 11 = 421
345 + 76 = 300 + 40 + 70 + 5 + 6 = 300 + 110 + 11 = 421
421 = 421
6 + 18 + 2 = 6 + 20
Применим сочетательное свойство: 6 + (18 + 2) = 6 + 20
Проверка:
6 + 18 + 2 = 6 + 20 = 26
6 + 20 = 26
26 = 26
26 + 0 = 26 – если к числу прибавить 0, то число не изменится.
Проверка:
26 + 0 = 26
26 = 26
0 + 19 = 19 – если к числу прибавить 0, то число не изменится.
Проверка:
0 + 19 = 19
19 = 19
18 – 0 = 18 – если из числа вычесть 0, то число не изменится.
Проверка:
18 – 0 = 18
18 = 18
0 + 0 = 0 – если к числу прибавить 0, то число не изменится.
Проверка:
0 + 0 = 0
0 = 0
Делаем вывод.
Равенства равны, так как справа и слева одинаковые значения.
Номер 2.
Реши уравнения, не вычисляя.
Ответ:x + 15 = 15
x = 0
18 − x = 18
x = 0
x − 27 = 0
x = 27
1) Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни правила сложения и вычитание с 0:
а + 0 = 0 + а = а;
а – 0 = а;
а – а = 0.
Рассмотрим уравнения и выполним вычисления.
Рассмотрим уравнение 1:
х + 15 = 15
х – неизвестное слагаемое.
Если к числу прибавить 0, то число не изменится.
х = 0
Рассмотрим уравнение 2:
18 – х = 18
х – неизвестное вычитаемое.
Если из числа вычесть 0, то число не изменится.
х = 0
Рассмотрим уравнение 3:
х – 27 = 0
х – неизвестное уменьшаемое.
Если из числа вычесть само это число, то разность равна нулю.
х = 27
Оформляем задание в тетрадь.
х + 15 = 15
х = 0
18 – х = 18
х = 0
х – 27 = 0
х = 27
Задание на полях страницы
Какие числа пропущены?

85 86 87 88 89 90 91 92 Закономерность выстроена так, что каждое следующее число на единицу больше предыдущего.
1) Для того, чтобы вставить пропущенные числа, необходимо увидеть закономерность.
2) Каждое следующее число при счете получается путем прибавления единицы к данному числу.
3) Каждое предыдущее число образуется путем вычитания единицы из данного числа.
Рассуждаем и выполняем вычисления.
Если рассмотреть ряд чисел, то числа идут по порядку при счете.
Закономерность: каждое следующее число больше предыдущего на 1.
85 + 1 = 86
86 + 1 = 87
87 + 1 = 88
88 + 1 = 89
89 + 1 = 90
90 + 1 = 91
90 + 1 = 92
Оформляем задание в тетрадь.
Ответ: 85; 86; 87; 88; 89; 90; 91; 92.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.