Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 99

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 2.
1) В году три осенних месяца: сентябрь, октябрь и ноябрь. Узнай по календарю, сколько дней длится осень; сколько недель она длится.
2) Используя календарь, составь и реши похожие задачи про зиму, весну и лето.
1) 30 + 31 + 30 = 91 (д.) – дней длится осень, это 13 недель.
2) Задача 1:
В году три зимних месяца: декабрь, январь и февраль. Узнай по календарю, сколько дней длится зима, сколько недель она длится.
Зима длится 90 или 91 день, в зиме 12 полных недель и 6 дней или полных 13 недель.
Задача 2:
В году три весенних месяца март, апрель, май. Узнай по календарю, сколько дней длится весна, сколько недель она длится.
Весна длится 92 дня; 13 недель.
Задача 3:
В году три летних месяца: июнь, июль, август. Узнай по календарю, сколько дней длится лето, сколько недель оно длится.
Лето длится 92 дня; 13 недель.
1) Помни о том, какие существуют единицы измерения времени: день, неделя, месяц, год.
2) Вспомни, какие месяцы входят в осень. Подумай, как понять, сколько длится осень.
Рассмотрим календарь.
Осень состоит из 3 месяцев: сентябрь, октябрь, ноябрь.

Сентябрь − 30 дней.
Октябрь − 31 день.
Ноябрь − 30 дней.
Рассуждаем.
Общая длительность осени складывается из длительности каждого месяца из которых она состоит. Значит, чтобы узнать, сколько длится осень, нужно сложить длительность каждого месяца.
30 + 31 + 30 = 91 (день) – длится осень.
Продолжаем рассуждение.
В неделе 7 дней, а всего в осени – 91 день. Значит, нам известна длительность осени и длительность одной недели, но мы не знаем, чему равно количество недель. Значит, чтобы узнать, сколько недель в осени, нужно общее количество дней разделить на количество дней в одной неделе.
91 : 7 = (70 + 21) : 7 = 70 : 7 + 21 : 7 = 10 + 3 = 13 (нед.) – длится осень.
Число 91 мы ещё не умеем делить на 7. Разложим число 91 на сумму чисел 70 и 21. Числа 70 и 21 разделим на 7.
Получим 70 : 7 = 10 и 21 : 7= 3, значит осенью 13 недель.
Записываем ответ.
Ответ: 91 день, 13 недель.
Аналогично рассуждаем, составляя и решая подобные задачи.
Составим задачу.
В году три зимних месяца: декабрь, январь и февраль. Узнай по календарю, сколько дней длится зима, сколько недель она длится.
Рассмотрим календарь.
Зима состоит из 3 месяцев: декабрь, январь и февраль.
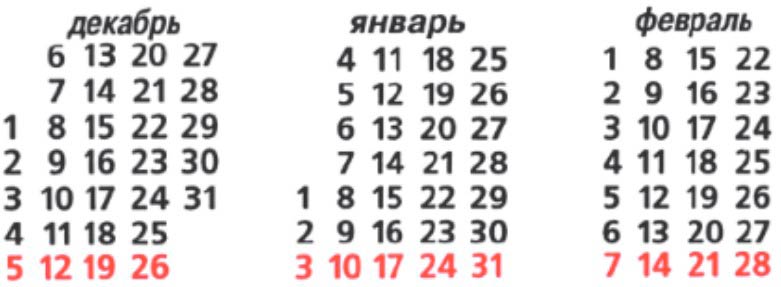
Декабрь – 31 день.
Январь – 31 день.
Февраль – 28 или 29 дней.
Рассуждаем.
Общая длительность зимы складывается из длительности каждого месяца из которых она состоит. Значит, чтобы узнать, сколько длится зима, нужно сложить длительность каждого месяца.
31 + 31 + 28 = 90 (дней) − длится зима в обычный год.
31 + 31 + 29 = 91 (день) − длится зима в високосный год.
Продолжаем рассуждение.
В неделе 7 дней, а всего зимой – 90 или 91 день. Значит, нам известна длительность зимы и длительность одной недели, но мы не знаем, чему равно количество недель. Значит, чтобы узнать, сколько недель в зиме, нужно общее количество дней разделить на количество дней в одной неделе.
90 : 7 = (70 + 14 + 6) : 7 = 70 : 7 + 14 : 7 и 6 дней = 10 + 2 и 6 дней = 12 нед. и 6 дней – в обычный год.
Число 90 нацело на 7 не делится. Разложим число 90 на сумму чисел 70, 14 и 6. Числа 70 и 14 разделим на 7, а число 6 оставим.
Получим 70 : 7 = 10 и 14 : 7= 2, значит зимой 12 недель и 6 день.
91 : 7 = (70 + 21) : 7 = 70 : 7 + 21 : 7 = 10 + 3 = 13 (нед.) – в високосный год.
Число 91 мы ещё не умеем делить на 7. Разложим число 91 на сумму чисел 70 и 21. Числа 70 и 21 разделим на 7.
Получим 70 : 7 = 10 и 21 : 7= 3, значит летом 13 недель.
Записываем ответ.
Ответ: 90 или 91 день, 12 недель и 6 дней или 13 недель.
Составим задачу.
В году три весенних месяца март, апрель, май. Узнай по календарю, сколько дней длится весна, сколько недель она длится.
Рассмотрим календарь.
Весна состоит из 3 месяцев: март, апрель и май.

Март – 31 день.
Апрель – 30 дней.
Май – 31 день.
Рассуждаем.
Общая длительность весны складывается из длительности каждого месяца из которых она состоит. Значит, чтобы узнать, сколько длится весна, нужно сложить длительность каждого месяца.
31 + 31 + 30 = 92 (дня) − длится весна.
Продолжаем рассуждение.
В неделе 7 дней, а всего в весне 92 дня. Значит, нам известна длительность весны и длительность одной недели, но мы не знаем, чему равно количество недель. Значит, чтобы узнать, сколько недель в весне, нужно общее количество дней разделить на количество дней в одной неделе.
92 : 7 = (70 + 21 + 1) : 7 = 70 : 7 + 21 : 7 и 1 день = 10 + 3 и 6 дней = 13 нед. и 1 дней – длится весна.
Число 92 нацело на 7 не делится. Разложим число 92 на сумму чисел 70, 21 и 1. Числа 70 и 21 разделим на 7, а число 1 оставим.
Получим 70 : 7 = 10 и 21 : 7 = 3, значит весной 13 недель и 1 день.
Записываем ответ.
Ответ: 92 дня; 13 недель и 1 день.
Составим задачу.
В году три летних месяца: июнь, июль, август. Узнай по календарю, сколько дней длится лето, сколько недель оно длится.
Рассмотрим календарь.
Лето состоит из 3 месяцев: июнь, июль, август.

Июнь – 30 дней.
Июль – 31 день.
Август – 31 день.
Рассуждаем.
Общая длительность лета складывается из длительности каждого месяца из которых оно состоит. Значит, чтобы узнать, сколько длится лето, нужно сложить длительность каждого месяца.
30 + 31 + 31 = 92 (дней) − длится лето.
Продолжаем рассуждение.
В неделе 7 дней, а всего летом – 92 дня. Значит, нам известна длительность лета и длительность одной недели, но мы не знаем, чему равно количество недель. Значит, чтобы узнать, сколько недель летом, нужно общее количество дней разделить на количество дней в одной неделе.
92 : 7 = (70 + 21 + 1) : 7 = 70 : 7 + 21 : 7 и 1 день = 10 + 3 и 6 дней = 13 нед. и 1 дней – длится лето.
Число 92 нацело на 7 не делится. Разложим число 92 на сумму чисел 70, 21 и 1. Числа 70 и 21 разделим на 7, а число 1 оставим.
Получим 70 : 7 = 10 и 21 : 7= 3, значит летом 13 недель и 1 день.
Записываем ответ.
Ответ: 92 дня; 13 недель и 1 день.
Номер 3.
Назови время, которое показывают часы, используя слова «четверть» и «половина».

Четверть первого. Без четверти час. Половина первого.
1) Помни, что у часов есть две стрелки – длинная и короткая. Длинная стрелка указывает на количество минут, а короткая – на количество часов.
2) Помни о соотношении числовых значений единиц времени.
3) Доля – одна часть из тех, на которые разделили целое.
4) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Четверть – это значит, одна четвертая часть, то есть 1 час разделили на четыре одинаковых части и взяли одну такую часть.
Вспомним, что 1 час = 60 минут.
Рассмотрим часы 1.
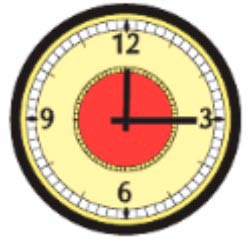
На часах показано одна четвертая часть от часа.
1 час составляет 60 минут. Этот час разделили на 4 части и взяли только одну.
Поэтому, чтобы узнать, сколько содержится в одной четвертой часа нужно разделить целый час в минутах на 4, потому что взяли четвёртую часть.
60 : 4 = 15 (мин) – четверть часа.
Рассмотрим часы 2.
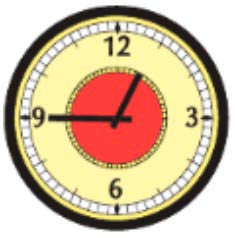
На часах показано, что до целого часа не хватает одной четвертой части до часа. Мы уже знаем, что она четвертая часа равна 15 минут. Чтобы узнать какое будет время на часах, нужно из целого часа в минутах вычесть недостающие 15 минут.
60 – 15 = 45 (мин.) – без четверти час.
Это значит, что до целого часа не хватает одной четвертой или не хватает 15 минут.
Рассмотрим часы 3.
На часах показано одна вторая часа или половина часа.
1 час составляет 60 минут. Этот час разделили на 2 части и взяли только одну.
Поэтому, чтобы узнать, сколько содержится в одной второй часа нужно разделить целый час в минутах на 2, потому что взяли вторую часть.
60 : 2 = 30 (мин) – половина часа или половина первого.
Оформляем задание в тетрадь.
1 часы − 15 (минут) − четверть первого часа.
2 часы − 45 (мин) – без четверти час.
3 часы − 30 (минут) − половина первого часа.
Номер 4.
Таня отрезала от ленты ее пятую часть – 8 дм. Найди длину всей ленты в дециметрах и вырази ее в метрах.
Ответ:
8 ∙ 5 = 40 (дм) – общая длина всей ленты 40 дм = 4 м Ответ: 4 м длина всей ленты.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде чертежа.
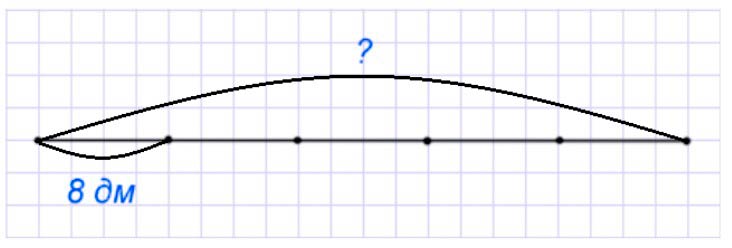
Рассуждаем.
Таня отрезала от ленты пятую часть. Пятая часть составляет 8 дм. Значит, длину ленты разделили на 5 частей и взяли только одну. Соответственно, зная длину части и количество частей можно узнать длину ленты, если длину части умножить на количество частей.
8 ∙ 5 = 40 (дм) − длина ленты.
Продолжаем рассуждение.
Выразим длину в метрах. Так как в 1 метре содержится 10 дециметров, то:
40 : 10 = 4 (м), так как 4 · 10 = 40.
Записываем ответ.
Ответ: длина ленты 4 метра.
Номер 5.
Петя купил упаковку корма для попугая. В упаковке 27 пакетиков. На сколько недель хватит попугаю этого корма, если каждую неделю он съедает по 3 пакетика корма?
Ответ:27 п. – ? н. 3 п. – 1 н. 27 : 3 = 9 (н.) хватит всего Ответ: на 9 недель хватит корма попугаю.
Данная задача: вида «кол-во обоев в 1 рулоне, кол-во рулонов, общее кол-во обоев» характеризуется зависимостями между компонентами:
Кол-во обоев в 1 рулоне · кол-во рулонов = общее кол-во обоев.
Общее кол-во обоев : кол-во рулонов = кол-во обоев в 1 рулоне.
Общее кол-во обоев : кол-во обоев в 1 рулоне = кол-во рулонов.
Оформляем условие в виде таблицы.
Каждую неделю попугай съедает по 3 пакетика корма. Значит, нам известен расход количества пакетиков в неделю, количество недель, но неизвестно общее количество пакетиков.
Заполняю всеми имеющимися данными таблицу:

Рассуждаю.
Из таблицы видно, что общее количество пакетиков, которые съедает попугай складывается из количества пакетиков, расходуемых в каждую неделю. Поэтому, чтобы узнать, на сколько недель хватит 27 пакетиков, нужно общее количество пакетиков разделить на расход пакетиков в 1 неделю.
27 : 3 = 9 (нед.) – хватит 27 пакетиков.
Записываем ответ.
Ответ: на 9 недель хватит корма.
Номер 6.
Проверь, правильно ли решены уравнения.
Ответ:у ∙ 6 = 42 у = 42 : 6 у = 7 7 ∙ 6 = 42 42 = 42 Решено правильно.

1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия умножения и деления и то, что является проверкой для решения уравнения.
Рассуждаем.
у · 6 = 42
у – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
56 : х = 7
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х : 9 = 6
х – неизвестное делимое.
Чтобы найти неизвестное делимое нужно значение частного умножить на делитель.
Решаем уравнение и сравниваем ответы.
y ∙ 6 = 42
y = 42 : 6
y = 7
Уравнение решено правильно, так как 7 = 7.
56 : x = 7
x = 56 : 7
x = 8
Уравнение решено неправильно, так как 8 < 49
x : 9 = 6
x = 6 ∙ 9
x = 54
Уравнение решено неправильно, так как 54 < 56
Записываем ответ.
Ответ: 1 равнение – верно; 2 уравнение – неверно; 3 уравнение – неверно.
Номер 7.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1 2
3 · 8 : 6 = 4
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2) 24 : 6 = 4,так как 6 · 4 = 24
1 2
6 · 4 : 3 = 8
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 6 ∙ 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
2) 24 : 3 = 8, где 3 · 8 = 24
1 2
9 ∙ 4 : 6 = 6
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 9 ∙ 4 = 36,
где 9 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
2) 36 : 6 = 6, так как 6 · 6 = 36
1 2
14 : 2 ∙ 7 = 49
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 14 : 2 = 7, так как 2 · 7 = 14
2) 7 ∙ 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
1 2
27 : 3 ∙ 9 = 81
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 27 : 3 = 9, так как 3 · 9 = 27
2) 9 ∙ 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
1 2
32 : 4 ∙ 8 = 64
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 32 : 4 = 8, так ка 4 · 8 = 32
2) 8 ∙ 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2 1
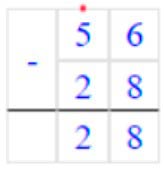
56 − (32 − 4) = 28
В данном выражении присутствуют действия вычитания и скобки. Вначале выполняем вычитание в скобках, а потом вычитание вне скобок.
1) 32 – 4 = 32 – (2 + 2) = (32 – 2) – 2 = 30 – 2 = 28
2) 56 − 28 = 28
2 1
85 – (65 + 20) = 0
В данном выражении присутствуют действия вычитания и скобки. Вначале выполняем вычитание в скобках, а потом вычитание вне скобок.
1) 65 + 20 = (60 + 20) + 5 = 80 + 5 = 85
2) 85 − 85 = 0
2 1
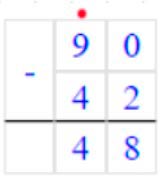
90 − (62 − 20) = 48
В данном выражении присутствуют действия вычитания и скобки. Вначале выполняем вычитание в скобках, а потом вычитание вне скобок.
1) 62 – 20 = (60 – 20) + 92 – 0) = 40 + 2 = 42
2) 90 − 42 = 48
0 : 9 = 0
0 : 24 = 0
0 ∙ 33 = 0
Если нуль разделить или умножить на число (не равное нулю), то получится нуль.
Оформляем задание в тетрадь.
3 · 8 : 6 = 24 : 6 = 4
6 · 4 : 3 = 24 : 3 = 8
9 · 4 : 6 = 36 : 6 = 6
14 : 2 · 7 = 7 · 7 = 49
27 : 3 · 9 = 9 · 9 = 81
32 : 4 · 8 = 8 · 8 = 64
56 – (32 – 4) = 56 – 28 = 28
85 – (65 + 20) = 85 – 85 = 0
90 – (62 – 20) = 90 – 42 = 48
0 : 9 = 0
0 : 24 = 0
0 · 33 = 0
Номер 8.
1) Из чисел 6, 2, 15 и 5 составь две суммы так, чтобы значение одной было в 3 раза меньше значения другой суммы.
2) Из тех же чисел составь две разности так, чтобы значение одной было в 3 раза больше значения другой разности.
1) 15 + 6 = 21
2 + 5 = 7
2) 15 − 6 = 9
5 − 2 = 3
1) «в 3 раза меньше», значит, вычисляется делением.
2) «в 3 раза больше», значит, вычисляется умножением.
Составим суммы.
Сумма – это результат сложения.
15 + 6 = 21 – первая сумма.
2 + 5 = 7 – вторая сумма.
Делаем проверку.
Проверяю, что значение одной суммы в 3 раза меньше значения другой:
21 : 7 = 3, так как 7 · 3 = 21.
Значит сумма (2 + 5) в 3 раза меньше суммы (15 + 6).
Составим разность.
Разность – это результат вычитания.
15 – 6 = 9 – первая разность.
5 – 2 = 3 – вторая разность.
Делаем проверку.
Проверяю, что значение одной разности в 3 раза больше значения другой:
9 : 3 = 3, так как 3 · 3 = 9.
Значит разность (15 – 6) в 3 раза больше разности (5 – 2).
Задание внизу страницы
Какую часть года составляют 3 месяца?
Ответ:12 : 3 = 4 (ч.) – составляют 3 месяца Ответ: 3 месяца составляют четвёртую часть года.
1) Помни о том, какие существуют единицы измерения времени: сутки, неделя, месяц, год.
Оформляем условие в виде краткой записи или чертежа.
Один год – целое, состоит из 12 месяцев.
Краткая запись:
Целое – 12 месяцев
? часть – 3 месяца.
Чертёж:
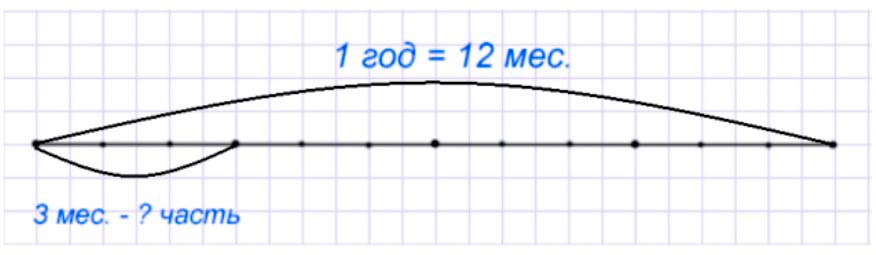
Рассуждаем.
Нам нужно узнать, какую часть составляют 3 месяца. Для этого, нужно общее количество месяцев разделить на количество одной части, чтобы узнать, какую часть года они составляют.
12 : 3 = 4 (часть) – составляет 3 месяца.
Значит, 3 месяца – это одна четвертая часть года.
Это значит весь год разделили на 4 равные части и взяли одну такую часть и это равно 3 месяцам.
Записываем ответ.
Ответ: 3 месяца – это четвертая часть года.
Задание на полях страницы
Набери множителями:

24 = 4 ∙ 6
24 = 24 ∙ 1
24 = 8 ∙ 3
24 = 6 ∙ 4
24 = 1 ∙ 24
24 = 3 ∙ 8
Вспомни зависимость между компонентами и результатом действия умножения и деления и то, что является проверкой для решения уравнения.
Устные рассуждения.
Умножая данные числа нужно набрать число 24.
Записываем произведения.
24 · 1 = 24,
где 24 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
8 · 3 = 24,
где 8 – одинаковое слагаемое, а 3 количество одинаковых слагаемых.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.