Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 77

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 10.
Реши уравнения, подбирая значения х.
Ответ:
х · 38 = 38
х = 38 : 38
х = 1
Проверка:
1 · 38 = 38
38 = 38
Ответ: х =1
х · 8 = 0
х = 0 : 8
х = 0
Проверка:
0 · 8 = 0
0 = 0
Ответ: х = 0
26 - х = 0
х = 26 - 0
х = 26
Проверка:
26 - 26 = 0
0 = 0
Ответ: х = 26
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия умножения и деления.
Рассмотрим уравнения.
х · 38 = 38
Данное уравнение основано на арифметическом действии умножения. Известен второй множитель и значение произведения. При этом они равны. Такое возможно только если первый множитель равен единице, потому что если 1 умножить на любое число, то получится это же число.
х · 8 = 0
Данное уравнение основано на арифметическом действии умножения. Известен второй множитель и значение произведения. При этом значение произведения равно нулю. Такое возможно, только если увеличивать ноль на любое число. Соответственно, первый множитель равен нулю.
26 – х = 0
Данное уравнение основано на арифметическом действии вычитания. Известно уменьшаемое и значение разности. При этом, значение разности равно нулю. Такое возможно, только если из числа вычитать это же число. Соответственно, вычитаемое равно уменьшаемому.
Решаем уравнение.
х · 38 = 38,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х · 8 = 0,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
26 – х = 0
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 26 – 0
х = 26
Выполняем проверку.
х · 38 = 38
Проверка: вместо неизвестного подставим число 1.
1 · 38 = 38
38 = 38 – верно.
х · 8 = 0
Проверка: вместо неизвестного подставим число 0.
0 · 8 = 0
0 = 0 – верно.
26 – х = 0
Проверка: вместо неизвестного подставим число 26.
26 – 26 = 0
0 = 0 – верно.
Оформляем задание в тетрадь.
х ∙ 38 = 38
Вспомни правило умножения на 1. Если число умножить на единицу, то получится тоже самое число.
х = 1.
х ∙ 8 = 0
Если произведение равно 0, то значит один из множителей тоже равен 0.
х = 0.
26 – х = 0
Если разность равно 0, то значит уменьшаемое и вычитаемое это одно и тоже число.
х = 26.
Номер 11.
Вспомни, как можно узнать неизвестное слагаемое, вычитаемое. Реши уравнения.
Ответ:
Вспомни названия компонентов действия вычитания и сложения, а также зависимости между компонентами и результатами действий сложения и вычитания.
Рассмотрим уравнения.
30 + х = 56,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
m – 14 = 80,
m – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
70 – к = 47,
к – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
Решаем уравнения.
30 + х = 56
х = 56 – 30
х = 26
m − 14 = 80
m = 80 + 14
m = 94
70 − k = 47
k = 70 − 47
k = 23
Выполним проверку.
30 + х = 56 Проверка: вместо неизвестного подставим число 26. 30 + 26 = 56
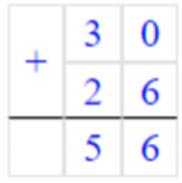
56 = 56 – верно.
m – 14 = 80
Проверка: вместо неизвестного подставим число 94.
94 – 14 = 80
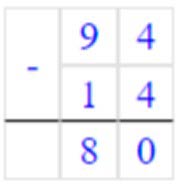
80 = 80 – верно.
70 - k = 47
Проверка: вместо неизвестного подставим число 23.
70 – 23 = 47
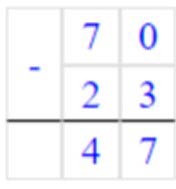
47 = 47 – верно
Оформляем задание в тетрадь.
30 + х = 56
Чтобы найти один из слагаемых, нужно из суммы вычесть второе слагаемое.
х = 56 – 30
х = 26
m − 14 = 80
Чтобы найти неизвестное уменьшаемое, нужно к разности и вычитаемое сложить.
m = 80 + 14
m = 94
70 − k = 47
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
k = 70 − 47
k = 23
Номер 12.
Сравни, не вычисляя, значения выражений.
Ответ:
7 ∙ 9 = 9 ∙ 7
63 = 63
7 + 9 = 9 + 7
16 = 16
38 – 4 < 38
34 < 38
36 : 4 > 36 : 6
9 > 6
7 ∙ 8 > 7 ∙ 7
56 > 49
7 + 8 > 7 + 7
15 > 14
1) Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
где а · 3,
а – первый множитель,
3 – количество множителей.
2) Помни о зависимости между компонентами и результатом действия умножения.
Рассмотрим выражения.
Рассмотрим 7 · 9 и 9 · 7,
Данные выражения равны по переместительному свойству умножения, потому что от перестановки мест множителей значение произведения не изменяются.
7 · 9 = 9 · 7
Ставим знак равно.
Рассмотрим 7 + 9 и 9 + 7
Данные выражения равны по переместительному свойству сложения, потому что от перестановки мест слагаемых значение суммы не изменяется.
7 + 9 = 9 + 7
Ставим знак равно.
Рассмотрим 38 – 4 и 38,
Выражение слева меньше, потому что в каждом из выражений левой и правой части есть один и тот же компонент: 38, но в левой части его уменьшают на 4 единицы, а в правой – с числом никаких действий не производят.
38 – 4 < 38
Ставим знак меньше.
Рассмотрим 36 : 4 и 36 : 6
Значение выражение слева больше, потому что в левой и правой части есть одно и то же число: 36. Но в левой части его уменьшают в 4 раза, а в правой – в 6 раз. При этом, 4 < 6, значит, значение выражения в левой части больше, чем значение выражения правой части.
36 : 4 > 36 : 6
Ставим знак больше.
Рассмотрим 7 · 8 и 7 · 7
Значение выражения слева больше, чем значение выражения справа, потому что одно и то же число в левой части повторяют 8 раз, а в правой – 7 раз.
7 · 8 > 7 · 7
Ставим знак больше.
Рассмотрим 7 + 8 и 7 + 7
Значение суммы в левой части больше, чем значение суммы в правой, потому что одно и то же число в левой части увеличивают на 8, а в правой – на 7.
7 + 8 > 7 + 7
Ставим знак больше.
Выполним проверку.
Проверим вычислением, что 7 · 9 = 9 · 7
7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 7= 63,
где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выражения равны.
Проверим вычислением, что 7 + 9 = 9 + 7
7 + 9 = 7 + (3 + 6) = (7 + 3) + 6 = 10 + 6 = 16
Представим число 9 в виде суммы чисел 3 и 6. Вначале к числу 7 прибавим число 3, а потом прибавим число 6.
9 + 7 = 9 + (1 + 6) = (9 + 1) + 6 = 10 + 6 = 16
Представим число 7 в виде суммы чисел 1 и 6. Вначале к числу 9 прибавим число 1, а потом прибавим число 6.
Выражения равны.
Проверяю вычислением, что 38 – 4 < 38
38 – 4 = (30 + 8) – 4 = 30 + (8 – 4) = 30 + 4 = 34
34 < 38
Первое выражение меньше, чем второе выражение.
Проверяю вычислением, что 36 : 4 > 36 : 6
36 : 4 = 9,
так как 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 6 = 6,
так как 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
9 > 6
Первое выражение больше, чем второе выражение.
Проверяю вычислением, что 7 · 8 > 7 · 7
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
56 > 49
Первое выражение больше, чем второе выражение.
Проверяю вычислением, что 7 + 8 > 7 + 7
7 + 8 = 7 + (3 + 5) = (7 + 3) + 5 = 10 + 5 = 15
Представим число 8 в виде суммы чисел 3 и 5. Вначале к числу 7 прибавим число 3, а потом прибавим число 5.
7 + 7 = 7+ (3 + 4) = (7 + 3) + 4 = 10 + 4 = 14
Представим число 7 в виде суммы чисел 3 и 4. Вначале к числу 7 прибавим число 3, а потом прибавим число 4.
15 > 14
Первое выражение больше, чем второе выражение.
Оформляем задание в тетрадь.
7 ∙ 9 = 9 ∙ 7 – от перемены места множителей произведение не меняется.
7 ∙ 9 = 63
9 ∙ 7 = 63
7 + 9 = 9 + 7 – от перестановки слагаемых сумма не меняется.
7 + 9 = 16
9 + 7 = 16
38 - 4 < 38 – если из числа вычесть другое число, то изначальное число уменьшиться.
38 – 4 = 34
34 < 38
36 : 4 > 36 : 6 – при одинаковом делимом, чем больше делитель, тем меньше частное, то есть если 4 < 6, то 36 : 4 > 36 : 6.
36 : 4 = 9
36 : 6 = 6
9 > 6
7 ∙ 8 > 7 ∙ 7 – при одинаковом первом множителе, чем больше второй множитель, тем больше и произведение, то есть если 8 > 7, то и 7 ∙ 8 > 7 ∙ 7.
7 ∙ 8 = 56
7 ∙ 7 = 49
56 > 49
7 + 8 > 7 + 7 - при одинаковом первом слагаемом, чем больше второй слагаемое, тем больше и сумма, то есть если 8 > 7, то и 7 + 8 > 7 + 7.
7 + 8 = 15
7 + 7 = 14
15 > 14
Номер 13.
Составь верные равенства и неравенства, используя выражения:
1) 9 ∙ 3, 30 − 6, 3 ∙ 9, 30 − 3;
2) 6 ∙ 9, 7 ∙ 8, 60 − 6, 32 + 8, 9 ∙ 6.
1) Равенства:
9 ∙ 3 = 3 ∙ 9
3 ∙ 9 = 30 − 3
9 ∙ 3 = 30 − 3
Неравенства:
3 ∙ 9 > 30 − 6
30 − 6 < 30 − 3
9 ∙ 3 > 30 − 6
2) Равенства:
30 − 3 = 9 ∙ 3
6 ∙ 9 = 60 − 6
60 − 6 = 9 ∙ 6
Неравенства:
7 ∙ 8 > 32 + 8
32 + 8 < 9 ∙ 6
32 + 8 < 60 − 6
1) Прежде, чем составлять верные равенства и неравенства, вычисли значение каждого выражения.
2) Равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знака равно.
3) равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знаков больше или меньше.
Вычислим значения выражений.
9 · 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
30 – 6 = 24
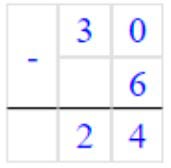
Вычитаем единицы. От числа 0 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 – 6 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 2 дес.,
Записываем в разряде десятков число 2.
Читаем ответ: 24.
3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
30 – 3 = 27
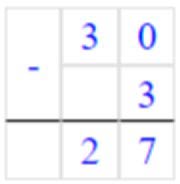
Вычитаем единицы. От числа 0 мы не можем отнять 3.
Занимаем 1 дес. = 10 ед., 10 - 3 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 72 дес.,
Записываем в разряде десятков число 2.
Читаем ответ: 27.
Составим равенства и неравенства.
Равенства:
9 ∙ 3 = 3 ∙ 9
3 ∙ 9 = 30 – 3
9 ∙ 3 = 30 − 3
Неравенства:
3 ∙ 9 > 30 – 6
30 − 6 < 30 − 3
9 ∙ 3 > 30 – 6
Вычислим значения выражений.
6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
60 – 6 = 54
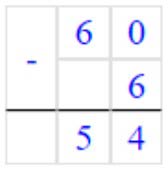
Вычитаем единицы. От числа 0 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 – 6 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. Было 6 дес., мы занимали 1 дес, осталось 6 – 1 = 5 дес.,
Записываем в разряде десятков число 5.
Читаем ответ: 54.
32 + 8 = 40
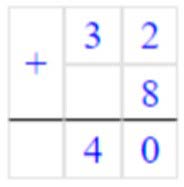
Складываем единицы. 2 + 8 = 10 – получилось 1 дес. и 0 ед.
Записываем в разряде единиц число 0, а 1 дес. запоминаем.
Складываем десятки. 1 дес. мы запомнили, занчит 3 + 1 = 4 – получилось десяток.
Записываем в разряде десятков число 4.
Читаем ответ: 40.
9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Составим равенства и неравенства.
Равенства:
30 − 3 = 9 ∙ 3
6 ∙ 9 = 60 − 6
60 − 6 = 9 ∙ 6
Неравенства:
7 ∙ 8 > 32 + 8
32 + 8 < 9 ∙ 6
32 + 8 < 60 – 6
Номер 14.
Ответ:8 ∙ 7 = 56 15 : 3 = 5 7 ∙ 9 = 63 54 : 9 = 6 8 ∙ 6 = 48 14 : 2 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Выполним умножение:
8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
8 · 6 = 48,
где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Выполним деление:
15 : 3 = 5,
так как 3 · 5 = 15,
где 3 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
54 : 9 = 6,
так как 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
14 : 2 = 7,
так как 2 · 7 = 14,
где 2 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Расставляем порядок действий и выполняем вычисления.
1 2
63 : 9 · 3 = 21
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 63 : 9 = 7, так ка 9 · 7 = 63
2) 7 ∙ 3 = 21
1 2
20 : 4 ∙ 8 = 40
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 20 : 4 = 5, так как 4 · 5 = 20
2) 5 ∙ 8 = 40
1 2
49 : 7 ∙ 4 = 28
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 49 : 7 = 7, так как 7 · 7 = 49
2) 7 ∙ 4 = 28
2 1
85 − (46 + 18) = 21
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – вычитание.
1) 46 + 18 = 64
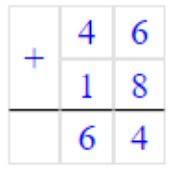
Складываем единицы. 6 + 8 = 14 – получилось 1 дес. и 4 ед.
Записываем в разряде единиц число 4, а 1 дес. запоминаем.
Складываем десятки. 4 + 1 = 5 и ещё 1 дес., который запомнили 5 + 1 = 6 – получилось десяток.
Записываем в разряде десятков число 6.
Читаем ответ: 64.
2) 85 − 64 = 21
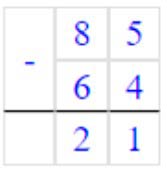
Вычитаем единицы. 5 − 4 = 1 – получилось единиц.
Записываем в разряде единиц число 1.
Вычитаем десятки. 8 − 6 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 21.
2 1
27 + (40 − 12) = 55
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – сложение.
1) 40 – 12 = 28
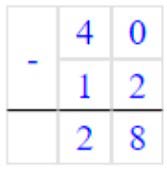
Вычитаем единицы. От числа 0 мы не можем отнять 2.
Занимаем 1 дес. = 10 ед., 10 – 2 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 4 дес., мы занимали 1 дес, осталось 4 – 1 = 3 дес.,
3 – 1 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 28.
2) 27 + 28 = 55
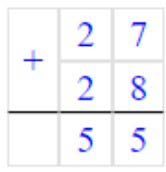
Складываем единицы. 7 + 8 = 15 – получилось 1 дес. и 5 ед.
Записываем в разряде единиц число 5, а 1 дес. запоминаем.
Складываем десятки. 2 + 2 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 55.
2 1
94 – (39 + 17) = 38
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – вычитание.
1) 39 + 17 = 56
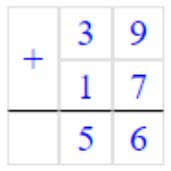
Складываем единицы. 9 + 7 = 16 – получилось 1 дес. и 6 ед.
Записываем в разряде единиц число 6, а 1 дес. запоминаем.
Складываем десятки. 3 + 1 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 56.
2) 94 − 56 = 38
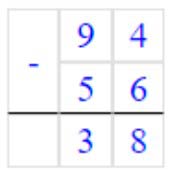
Вычитаем единицы. От числа 4 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 + 4 = 14 ед., 14 – 6 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 9 дес., мы занимали 1 дес, осталось 9 – 1 = 8 дес.,
8 – 5 = 3 – получилось десятков.
Записываем в разряде десятков число 3.
Читаем ответ: 38.
Oформляем задание в тетрадь.
8 ∙ 7 = 56
7 ∙ 9 = 63
8 ∙ 6 = 48
15 : 3 = 5
54 : 9 = 6
14 : 2 = 7
63 : 9 · 3 = 7 · 3 = 21
20 : 4 · 8 = 5 · 8 = 40
49 : 7 · 4 = 7 · 4 = 28
85 – (46 + 18) = 85 – 64 = 21
27 + (40 – 12) = 27 + 23 = 50
94 – (39 + 17) = 94 – 56 = 38
Номер 15.
1) Какие из чисел от 18 до 81 делятся на 9?
2) Какие из чисел: 16, 24, 32 – делятся без остатка на 4? на 3? на 8? на 6?
3) Запиши три числа, которые делятся и на 2, и на 3. Проверь, делятся ли эти числа на 6.
1) 18, 27, 36, 45, 54, 63, 72, 81. 2) на 4 : 16, 24, 32; на 8 : 16, 24, 32; на 3 : 24; на 6 : 24. 3) на 2 и на 3 : 6, 12, 18, 6 : 6 = 1, 12 : 6 = 2, 18 : 6 = 3.
1)делятся на 9, т.е. являются результатом таблицы умножения 9.
2)Без остатка на 4, 3, 8, 6, т.е. делятся нацело.
3)Делятся и на 2 и на 3, т.е. одновременно, в одно и то же время.
Рассмотрим задание 1.
Вспомним таблицу умножения на 9.
Результат умножения на 9 и есть числа, которые делятся на 9 без остатка.
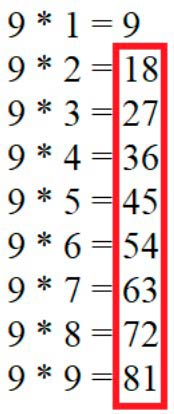
Значит, выписываю числа: 18, 27, 36, 45, 54, 63, 72, 81.
Рассмотрим задание 2.
Числа, которые делятся без остатка на 4:
16 : 4 = 4, так как 4 · 4 = 16,
где 4 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
24 : 4 = 6, так как 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
32 : 4 = 8, так как 4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Числа, которые делятся без остатка на 3:
16 : 3 – не делится,
так как нет такого числа, которое при умножении на 3 дал бы результат 16.
24 : 3 = 8, так как 3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
32 : 3 – не делится,
так как нет такого числа, которое при умножении на 3 дал бы результат 32.
Числа, которые делятся без остатка на 8:
16 : 8 = 2, так как 8 · 2 = 16,
где 8 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
24 : 8 = 3, так как 8 · 3 = 24,
где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
32 : 8 = 4,так как 8 · 4 = 32,
где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Числа, которые делятся без остатка на 6:
16 : 6 - не делится,
так как нет такого числа, которое при умножении на 6 дал бы результат 16.
24 : 6 = 4, так как 6 · 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
32 : 6 – не делится,
так как нет такого числа, которое при умножении на 6 дал бы результат 32.
Рассмотрим задание 3.
Рассмотрим числа, которые делятся на 2:
2, 4, 6, 8, 10, 12, 14, 16, 18.
Рассмотрим числа, которые делятся на 3:
3, 6, 9, 12, 15, 18, 21.
Числа, которые будут делится и на 2 и на 3:
6, 12, 18.
Числа, которые делятся и на и на 3, так же будут делится и на 6.
6 : 6 = 1, так как 6 · 1 = 6
12 : 6 = 2, так как 6 · 2 = 12
18 : 6 = 3, так как 6 · 3 = 18
Оформляем задание в тетрадь.
1) на 9 делятся: 18, 27, 36, 45, 54, 63, 72, 81.
18 : 9 = 2
27 : 9 = 3
36 : 9 = 4
45 : 9 = 5
54 : 9 = 6
63 : 9 = 7
72 : 9 = 8
81 : 9 = 9
2) на 4 делятся: 16, 24, 32.
16 : 4 = 4
24 : 4 = 6
32 : 4 = 8
на 3 делятся: 24
24 : 3 = 8
на 8 делятся: 16, 24, 32.
16 : 8 = 2
24 : 8 = 3
32 : 8 = 4
на 6 делится: 24
24 : 6 = 4
3) если число делится на 2 и на 3, значит оно делится на 6.
на 2 и на 3 делятся числа 6, 12, 18.
6 : 6 = 1
12 : 6 = 2
18 : 6 = 3
Номер 16.
9 одинаковых блокнотов стоят 72 р.
1) Сколько стоят 7 таких блокнотов? 4 блокнота? 2) Сколько таких блокнотов можно купить на 40 р.? на 64 р.?
Ответ:
Задача 1.
1) 72 : 9 = 8 (р.) – стоит один блокнот. 2) 8 ∙ 7 = 56 (р.) – стоит 7 блокнотов. 3) 8 ∙ 4 = 32 (р.) – стоят 4 блокнота Ответ: 56 рублей, 32 рубля.
Задача 2.
1-й способ решения: 1) 72 : 9 = 8 (р.) – стоит 1 блокнот. 2) 40 : 8 = 5 (б.) – можно купить на 40 рублей. 3) 64 : 8 = 8 (б.) – можно купить на 4 рубля. Ответ: 5 блокнотов и 8 блокнотов.
2-й способ решения: 1) 72 : 9 = 8 (р.) – стоит 1 блокнот. 2) 8 ∙ 7 = 56 (р.) – стоит 7 блокнотов. 3) 8 ∙ 4 = 32 (р.) – стоит 4 блокнота. 4) 40 : 8 = 5 (б.) 5) 64 : 8 = 8 (б.) Ответ: 56 рублей стоят 7 блокнотов и 32 рубля стоят 4 блокнота; 5 блокнотов можно купить на 40 рублей и 8 блокнотов можно купить на 64 рубля.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена блокнота · количество блокнотов = общая стоимость блокнотов.
Общая стоимость блокнотов : цена блокнота = количество блокнотов.
Общая стоимость блокнотов : количество блокнотов = цена блокнота.
Оформляем условие в виде таблицы.
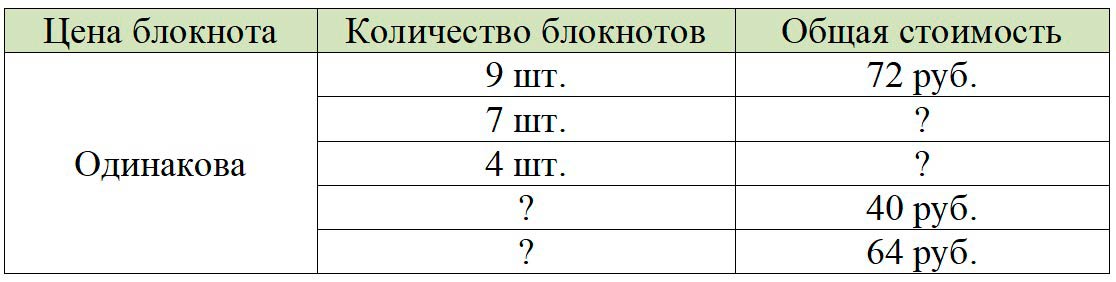
Рассуждаем.
Из таблицы видно, что цена блокнота одинаковая. А чтобы узнать сколько стоит 1 блокнот, нужно общую стоимость блокнота разделить на количество блокнотов.
72 : 9 = 8 (р.) – стоит один блокнот.
Решаем первую часть задачи.
Общая стоимость всех блокнотов складывается из стоимости каждого из семи блокнотов. Значит, чтобы узнать, сколько стоит 7 блокнотов, нужно сложить стоимости всех блокнотов.
Но цена блокнота одинаковая, поэтому сложением одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько стоят все блокноты вместе, нужно цену блокнота умножить на количество.
8 ∙ 7 = 56 (р.) – стоит 7 блокнотов.
Рассуждаем.
Чтобы узнать, сколько стоит 4 блокнота, нужно сложить стоимости всех блокнотов.
Но цена блокнота одинаковая, поэтому сложением одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько стоят все блокноты вместе, нужно цену блокнота умножить на количество.
8 ∙ 4 = 32 (р.) – стоят 4 блокнота.
Решаем вторую часть задачи.
Общая стоимость всех блокнота складывается из стоимостей каждого из блокнотов. Поэтому, чтобы узнать, сколько блокнотов купили, нужно общую стоимость блокнотов разделить на цену блокнота.
40 : 8 = 5 (б.) – можно купить на 40 рублей.
Рассуждаем.
Общая стоимость всех блокнота складывается из стоимостей каждого из блокнотов. Поэтому, чтобы узнать, сколько блокнотов купили, нужно общую стоимость блокнотов разделить на цену блокнота.
64 : 8 = 8 (б.) – можно купить на 64 рубля.
Оформляем решение по действиям.
1) 72 : 9 = 8 (р.) – стоит один блокнот.
2) 8 ∙ 7 = 56 (р.) – стоит 7 блокнотов.
3) 8 ∙ 4 = 32 (р.) – стоят 4 блокнота.
4) 40 : 8 = 5 (б.) – можно купить на 40 рублей.
5) 64 : 8 = 8 (б.) – можно купить на 64 рубля.
Записываем ответ.
Ответ: 56 рублей и 32 рубля; 5 блокнотов и 8 блокнотов.
Номер 17.
Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?
Ответ:
1-й способ решения: 1) 15 : 5 = 3 (м) – одна занавеска. 2) 21 : 3 = 7 (з.) – можно сшить из 21 м тюля. 3) 9 ∙ 3 = 27 (м) – тюли понадобится для 9 занавесок. Ответ: 7 занавесок можно сшить из 21 м тюля; 27 м тюля нужно на пошив 9 занавесок.
2-й способ решения: 21 : (15 : 5) = 21 : 3 = 7 (з.) – можно сшить из 21 тюля. 15 : 5 ∙ 9 = 3 ∙ 9 = 27 (м) – тюли понадобится для 9 занавесок. Ответ: 7 занавесок; 27 м тюля.
Данная задача: вида «расход на 1 занавеску, количество занавесок, общее количество тюля» характеризуется зависимостями между компонентами:
Расход на 1 занавеску · кол-во занавесок = общее кол-во тюля.
Общее кол-во тюля : кол-во занавесок = расход на 1 занавеску.
Общее кол-во тюля : расход на 1 занавеску = кол-во занавесок.
Оформляем условие в виде таблицы.
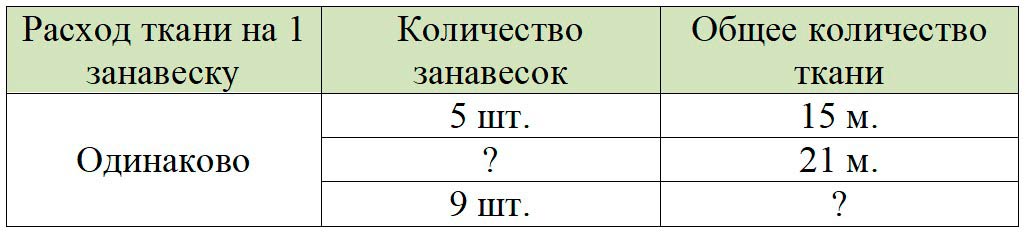
Рассуждаем.
Из таблицы видно, что общее количество ткани складывается из суммы ткани, расходуемой на каждую занавеску. Значит, чтобы узнать расход на 1 занавеску, нужно общее количество ткани разделить на количество занавесок.
15 : 5 = 3 (м) – пойдёт на одну занавеску.
Продолжаем рассуждение.
Мы узнали, что расход ткани на 1 занавеску равно 3 м. Теперь нам известно общее количество ткани. Значит, нам известен расход ткани на 1 занавеску, общее количество ткани, но неизвестно, сколько таких занавесок сшили.
Чтобы узнать, сколько занавесок сшили, нужно общее количество ткани разделить на расход ткани на 1 занавеску.
21 : 3 = 7 (з.) – можно сшить из 21 м тюля.
Рассуждаем.
Из таблицы видно, что общее количество ткани складывается из количества ткани, расходуемое на пошив каждой из 9 занавесок. Значит, чтобы узнать общее количество ткани, нужно расход ткани на каждую занавеску сложить.
Но количество ткани, расходуемое на 1 занавеску одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 3 = 27 (м) – тюли понадобиться для 9 занавесок.
Записываем ответ.
Ответ: 7 занавесок; 27 м тюля.
Номер 18.
Из каких трех фигур можно сложить треугольник? Запиши их номера.
Начерти и вырежи такой треугольник. Покажи сгибанием, что этот треугольник – симметричная фигура.

Из фигур №1, №2, №3.

Решить задачу проще, если производить реальные действия, т.е. начертить такие фигуры и вырезать их из листа клетчатой бумаги, а затем – сложить из них прямоугольник.
Составим треугольник двумя способами.
1 вариант: из фигур - 1, 2, 3.
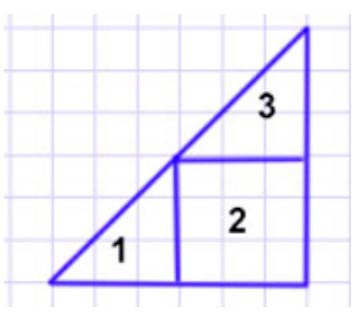
2 вариант: из фигур - 1, 3, 4.
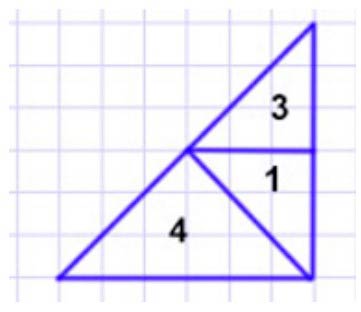
Ось симметрии.
Ось симметрии – это линия, по которой можно сложить фигуру так, что две части при налодении совпаут, а площадь частей будут равны.
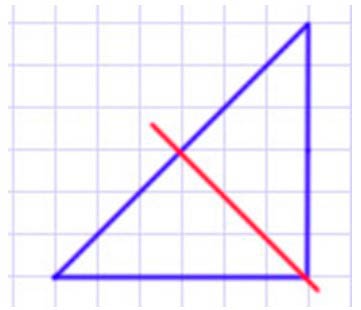
Ось симметрии обозначена красной линией.
Номер 25.
Назови наибольшее число до 30, которое делится на 7; на 8; на 9.
Ответ:На 7: 28. На 8: 24. На 9: 27.
1) Делится нацело на 7, 8, 9, т.е. делится без остатка.
2) Вспомни таблицу умножения чисел 7, 8, 9.
Вносним таблицы умножения на 7, на 8 и на 9.
.jpg)
Рассуждаем.
В таблице умножения найдём наибольшее частное, которе не больше 30.
Меньше 30, значит, расположено на луче натуральных чисел левее чсила 30.
Отчеркнём и затем в каждом столбце выберем наибольшее частное.
Оформляем задание в тетрадь.
На 7 – это число 28.
28 : 7 = 4
На 8 – это число 24.
24 : 8 = 3
На 9 – это число 27.
27 : 9 = 3.
Номер 26.
В первый класс школы в этом году поступили 67 человек. Их распределили по классам так: в 1 А — 22 ученика, в 1 Б — столько же, в 1 В — остальных детей. Сколько учеников в 1 В классе?
Ответ:Всего — 67 уч. 1 А — 22 уч. 1 Б — 22 уч. 1 В — ? уч. 1) 22 + 22 = 44 (уч.) — в 1 А и 1 Б 2) 67 – 44 = 23 (уч.) Ответ: 23 ученика в 1 В классе.
«всего», значит вычисляется сложением.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
В 1А распределили 22 ученика, а в 1Б – столько же. Общее количество детей, которые были там, складывается из количества детей обоих классов. Значит, чтобы узнать, сколько детей было в 1А и 1Б классе, нужно сложить количество детей обоих классов.
22 + 22 = 44 (уч.) – в 1 А и 1 Б.
Продолжаем рассуждение.
Общее количество детей в первых классах складывается из количества детей 1А, 1Б и 1В классов. Значит, чтобы узнать, сколько детей было в 1В классе, нужно из общего количества детей вычесть общее количество детей 1А и 1Б.
67 – 44 = 23 (уч.) – 1 В.
Записываем ответ.
Ответ: 23 ученика в 1 В классе.
Решение выражением: 67 – (22 + 22) = 23 (уч.), где 22 + 22 – количество детей в 1А и 1Б.
Рассмотрим все решения задачи.
Выражение основано на правиле вычитания суммы из числа. Вычислить значение выражения можно тремя способами, поэтому и решения задачи существует тоже три:
Решение 1:
67 – (22 + 22) = 67 – 44 = 23
В первом действии вычисляю количество детей, которые учатся в 1А и 1Б, а во втором – сколько детей учатся в 1В классе.
Решение 2:
67 – (22 + 22) = (67 – 22) – 22 = 45 – 22 = 23
В первом действии вычисляю, сколько всего детей в 1Б и 1В, а во втором – сколько детей в 1В классе.
Решение 3:
67 – (22 + 22) = (67 – 22) – 22 = 45 – 22 = 23
В первом действии вычисляю, сколько всего детей в 1А и 1В, а во втором – сколько детей в 1В классе.
Номер 27.
Во сколько раз 7 меньше, чем 28? чем 42? Во сколько раз 48 больше, чем 6? чем 8? На сколько 74 больше, чем 20? чем 12? чем 4? На сколько 18 меньше, чем 40? чем 28? чем 80?
Ответ:28 : 7 = 4 раза 42 : 7 = 6 раз 48 : 6 = 8 раз 48 : 8 = 6 раз. 74 − 20 = 54 раза 74 − 12 = 62 раза 74 − 4 = 70 раз 40 − 18 = 22 раза 28 − 18 = 10 раз 80 − 18 = 62 раза
1) Чтобы понять, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Вычисляется делением.
2) Чтобы понять, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее. Вычисляется делением.
3) Чтобы понять, на сколько одно число большее другого, нужно из большего числа вычесть меньшее. Вычисляется вычитанием.
4) Чтобы понять, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее. Вычисляется вычитанием.
Рассмотрим задание 1.
28 : 7 = 4, так как 7 · 4 = 28,
где 7 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Число 7 меньше числа 28 в 4 раза.
42 : 7 = 6, так как 7 · 6 = 42,
где 7 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Число 7 меньше числа 42 в 6 раз.
Рассмотрим задание 2.
48 : 6 = 8, так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Число 48 больше числа 6 в 8 раз.
48 : 8 = 6, так как 8 · 6 = 48,
где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Число 48 больше числа 8 в 6 раз.
Рассмотрим задание 3.
74 – 20 = (70 – 20) + 4 = 50 + 4 = 54
Число 74 представим в виде суммы чисел 70 и 4. Вначале из числа 70 вычтем число 20, а потом к полученной разности прибавим число 4.
Число 74 больше числа 20 на 54.
74 – 12 = 74 – (4 + 8) = (74 – 4) – 8 = 70 – 8 = 62
Число 12 представим в виде суммы чисел 4 и 8. Вначале из числа 74 вычтем число 4, а потом вычтем число 8.
Число 74 больше числа 12 на 62.
74 – 4 = 70 + (4 – 4) = 70 + 0 = 70
Число 74 представим в виде суммы чисел 70 и 4. Вначале из числа 4 вычтем число 4, а потом к полученной разности прибавим число 70.
Число 74 больше числа 4 на 70.
Рассмотрим задание 4.
40 – 18 = 40 – (10 + 8) = (40 – 10) – 8 = 30 – 8 = 22
Число 18 представим в виде суммы чисел 10 и 8. Вначале из числа 40 вычтем число 10, а потом вычтем число 8.
Число 18 меньше числа 40 на 22.
28 – 18 = 28 – (10 + 8) = (28 – 8) – 10 = 20 – 10 = 10
Число 18 представим в виде суммы чисел 10 и 8. Вначале из числа 28 вычтем число 8, а потом вычтем число 10.
Число 18 меньше числа 28 на 10.
80 – 18 = 80 – (10 + 8) = (80 – 10) – 8 = 70 – 8 = 62
Число 18 представим в виде суммы чисел 10 и 8. Вначале из числа 80 вычтем число 10, а потом вычтем число 8.
Число 18 меньше числа 80 на 62.
Номер 28.

Увеличь в 8 раз
1 ∙ 8 = 8
9 ∙ 8 = 72
3 ∙ 8 = 24
6 ∙ 8 = 48
7 ∙ 8 = 56
4 ∙ 8 = 32
Уменьши в 9 раз
27 : 9 = 3
45 : 9 = 5
72 : 9 = 8
36 : 9 = 4
54 : 9 = 6
63 : 9 = 7
1) Увеличь в 8 раз, т.е. умножь на 8.
2) Уменьши в 9 раз, т.е. раздели на 9.
Промежуточные вычисления.
Увеличь в 8 раз – это значит данное число умножить на 8.
1 · 8 = 8,где 1 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Уменьши в 9 раз – это значит данное число разделить на 9.
27 : 9 = 3,
так как 9 · 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
45 : 9 = 5,
так как 9 · 5 = 45,
где 9 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
72 : 9 = 8,
так как 9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
36 : 9 = 4,
так как 9 · 4 = 36,
где 9 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
54 : 9 = 6,
так как 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
63 : 9 = 7,
так как 9 · 7 = 63,
где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
Увеличь в 8 раз – это значит умножить на 8.
1 ∙ 8 = 8
9 ∙ 8 = 72
3 ∙ 8 = 24
6 ∙ 8 = 48
7 ∙ 8 = 56
4 ∙ 8 = 32
Уменьши в 9 раз – это значит разделить на 9.
27 : 9 = 3
45 : 9 = 5
72 : 9 = 8
36 : 9 = 4
54 : 9 = 6
63 : 9 = 7
Номер 29.
35 + 15 : 5 + 2 (35 + 15) : 5 + 2 42 : 6 · 7 32 : 4 · 8 63 : 7 · 5 81 : 9 · 6
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
2 1 3
35 + 15 : 5 + 2 = 40
В данном выражении присутствуют действия сложения и деление. Вначале выполняем действие деление, а потом сложения по порядку слева направо.
1 2 3
(35 + 15) : 5 + 2 = 12
В данном выражении присутствуют действия сложения и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом действие деление и последним – действие сложение вне скобок.
1 2
42 : 6 · 7 = 49
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1 2
32 : 4 · 8 = 64
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1 2
63 : 7 · 5 = 45
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку сева направо.
1 2
81 : 9 · 6 = 54
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку сева направо.
Выполняем вычисления по действиям.
2 1 3
35 + 15 : 5 + 2 = 40
1) 15 : 5 = 3, так как 5 · 3 = 15
2) 35 + 3 = 38
3) 38 + 2 = 40
1 2 3
(35 + 15) : 5 + 2 = 12
1) 35 + 15 = 50
2) 50 : 5 = 10, так как 5 · 10 = 50
3) 10 + 2 = 12
1 2
42 : 6 · 7 = 49
1) 42 : 6 = 7, так как 6 · 7 = 42
2) 7 ∙ 7 = 49
1 2
32 : 4 · 8 = 64
1) 32 : 4 = 8, так как 4 · 8 = 32
2) 8 ∙ 8 = 64
1 2
63 : 7 · 5 = 45
1) 63 : 7 = 9, так как 7 · 9 = 63
2) 9 ∙ 5 = 45
1 2
81 : 9 · 6 = 54
1) 81 : 9 = 9, так как 9 · 9 = 81
2) 9 ∙ 6 = 54
Оформляем задание в тетрадь.
35 + 15 : 5 + 2 = 35 + 3 + 2 = 35 + 5 = 40
(35 + 15) : 5 + 2 = 50 : 5 + 2 = 10 + 2 = 12
42 : 6 · 7 = 7 · 7 = 49
32 : 4 · 8 = 8 · 8 = 64
63 : 7 · 5 = 9 · 5 = 45
81 : 9 · 6 = 9 · 6 = 54
Номер 30.
Площадь листа цветной бумаги 100 см2. Из него вырезали 9 квадратов, площадью по 9 см2 каждый. Найди площадь оставшейся части листа цветной бумаги.
Ответ:Было — 100 см2 Вырезали — 9 кв. по 9 см2 Осталось — ? см2 1) 9 · 9 = 81 (см2) — площадь вырезанных квадратов. 2) 100 – 81 = 19 (см2) Ответ: 19 см2 площадь оставшейся части.
1) Помни, что у прямоугольника есть две величины, необходимые для вычисления площади: длина и ширина.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Оформляем условие в виде краткой записи.
Было – 100 см2 Вырезали – 9 кв. по 9 см2 Осталось – ?
Рассуждаем.
Общая площадь фигуры складывается из площадей всех фигур, из которых состоит большая фигура.
Значит, чтобы узнать, какова площадь вырезанной части, нужно узнать сумму площадей всех маленьких квадратов. Получается, нужно сложить площадь каждого маленького квадрата.
Но площадь маленького квадрата одинаковая. Значит, сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 9 = 81 (см2) – площадь вырезанных квадратов.
Продолжаем рассуждение.
Мы узнали, что общая площадь квадрата складывается из площади вырезанной части и оставшейся.
Значит, чтобы узнать, фигура с какой площадью осталась, нужно из площади большого квадрата вычесть площадь вырезанной части.
100 − 81 = 19 (см2) – площадь оставшейся части.
Записываем ответ.
Ответ: 19 площадь оставшейся части.
Решение выражением: 100 – 9 · 9 = 19 (см2), где 9 · 9 – площадь вырезанной части.
Номер 31.
Сделай чертёж к задаче и реши её.
От прямоугольника, длины сторон которого 5 см и 3 см, отрезали полоску со сторонами 3 см и 1 см. Найди площадь оставшейся части.

1) 5 – 1 = 4 (см) — длина оставшейся части. 2) 4 · 3 = 12 (см2) Ответ: 12 см2 площадь оставшейся части.
1) Площадь фигуры измеряется в квадратных единицах.
2) Помни, что у прямоугольника есть две величины, необходимые для вычисления площади: длина и ширина.
3) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Оформляем условие в виде чертежа.
.jpg)
Рассуждаем.
Длина стороны большого прямоугольника складывается из длины оставшейся части и отрезанной.
Значит, чтобы узнать, какова длина оставшегося прямоугольника, нужно из длины большого прямоугольник отнять длину маленького.
5 – 1 = 4 (см) – длина оставшейся части.
Продолжаем рассуждение.
Мы узнали недостающую длину оставшейся части. Нам известна другая сторона – 3 см.
Площадь прямоугольника произведение двух его сторон. Значит, чтобы узнать, какова площадь оставшейся части, нужно длину умножить на ширину.
4 ∙ 3 = 12 (см2) – площадь оставшейся части.
Записываем ответ.
Ответ: 12 см2 площадь оставшейся части.
Решение выражением: (5 – 1) · 3 = 12 (см2), где 5 – 1 – длина оставшейся части.
Номер 32.
Начерти план участка прямоугольной формы со сторонами 4 м и 9 м, изображая 1 м2 одной клеткой. Покажи на плане, что огурцами занято 12 м2, а помидорами — на 4 м2 больше, чем огурцами. Сколько квадратных метров участка остались свободными?
Ответ:
1) 12 + 4 = 16 (м2) — занято помидорами. 2) 2 · 4 = 8 (м2) — осталось свободными. Ответ: 8 м2
1) Площадь фигуры измеряется в квадратных единицах.
2) Помни, что у прямоугольника есть две величины, необходимые для вычисления площади: длина и ширина.
3) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
4) «на 4 м2 больше», значит, вычисляется вычитанием.
Рассуждаем.
Для начала, чтобы понять, сколько клеток всего умещается на плане участка на чертеже, нужно вычислить площадь участка в реальном масштабе.
Для того, чтобы вычислить площадь участка, нужно длину умножить на ширину.
4 ∙ 9 = 36 (м2) – площадь участка.
Теперь мы знаем, что площадь участка в реальном масштабе – 36 м2, тогда весь чертеж должен состоять из 36 клеток.
Продолжаем рассуждение.
Огурцами занято 12 м2, значит 12 клеток, а помидорами – на 4 м2 больше, чем огурцами. На 4 м2 больше, значит, что столько же, сколько огурцами и еще 4 м2.
12 + 4 = 16 (м2) – площадь под помидоры.
Продолжаем рассуждение.
Чтобы узнать сколько занято под овощи, нужно сложить площадь под огурцы и площадь под помидоры.
12 + 16 = 28 (м2) – занято под овощи или засаженная часть.
Продолжаем рассуждение.
При этом мы знаем, что общая площадь участка складывается из площадей частей, засаженных огурцами, помидорами и свободной.
Значит, чтобы узнать, какая часть участка свободна, нужно из общей площадь участка вычесть площадь засаженной.
36 – 28 = 8 (м2) – осталось.
Начертим план участка.
Чтобы начертить план нужно узнать длину каждой части. Известно, что ширина та же – 4 м, где 1 м на местности равен 1 клетки на плане.
12 : 4 = 3 (м) – длина под огурцы.
16 : 4 = 4 (м) – длина под помидоры.
8 : 4 = 2 (м) – длина оставшейся части.
.jpg)
Записываем ответ.
Ответ: 8 м2 свободно.
Задание на полях страницы.

42 : 6 = 7 28 : 4 = 7 56 : 8 = 7 21 : 7 = 3 35 : 5 = 7 70 : 10 = 7 63 : 9 = 7 Ответ: Лишнее выражение: 21 : 7 = 3, потому что значение выражения равно 3, а в других выражениях значение равно 7.
Чтобы понять, какое выражение лишнее, рассмотри все с разных точек зрения: из каких компонентов состоит, на каком арифметическом действии основано и наконец, каково значение каждого выражения.
Вычислим и сравним значения всех выражений.
42 : 6 = 7, так как 6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
28 : 4= 7, так как 4 · 7 = 28, где 4 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
56 : 8 = 7, так как 8 · 7 = 56, где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
21 : 7 = 3, так как 7 · 3 = 21, где 7 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
35 : 5 = 7, так как 5 · 7 = 35, где 5 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
70 : 10 = 7, так как 10 · 7 = 70, где 10 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
63 : 9 = 7, так как 9 · 7 = 63, где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Делаем вывод.
Лишнее выражение – 21 : 7 = 3, потому что значение этого равенства отличается от значений других выражений, в остальных примерах частное равно 7.
Записываем ответ.
Ответ: выражение 21 : 7 = 3 – лишнее.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.