Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 76

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Что узнали. Чему научились
Номер 1.
В новом пятиэтажном доме 80 квартир. На каждом этаже заселили по 8 квартир. Сколько квартир осталось заселить?
Ответ:
Всего – 80 кв.
Заселили – 5 эт. по 8 кв.
Осталось – ? кв.
1-й способ решения:
1) 8 ∙ 5 = 40 (кв.) – заселили.
2) 80 − 40 = 40 (кв.)
Ответ: 40 квартир осталось заселить в новом доме.
2-й способ решения: 80 - 8 ∙ 5 = 80 – 40 = 40 (кв.) – осталось. Ответ: 40 квартир.
Данная задача: вида «кол-во квартир на этаже, кол-во этажей, общее кол-во квартир» характеризуется зависимостями между компонентами:
Кол-во квартир на этаже · кол-во этажей = общее кол-во квартир.
Общее кол-во квартир : кол-во квартир на этаже = кол-во этажей.
Общее кол-во квартир : кол-во этажей = кол-во квартир на этаже.
Оформляем условие в виде краткой записи.
Всего – 80 кв.
Заселили – 5 эт. по 8 кв.
Осталось – ? кв.
Рассуждаем.
Общее количество квартир на всех этажах складывается из количества квартир на каждом этаже. Поэтому, чтобы узнать, сколько квартир было на всех этажах, нужно сложить количество квартир на каждом из 5 этажей.
Но количество квартир на каждом этаже одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.
8 ∙ 5 = 40 (кв.) – всего заселили.
Продолжаем рассуждение.
Общее количество квартир складывается из количества квартир, которые уже заселили и тех, что заселить осталось. Соответственно, чтобы узнать, сколько квартир осталось заселить, нужно из общего количества квартир вычесть количество заселенных.
80 − 40 = 40 (кв.) – осталось заселить.
Записываем ответ.
Ответ: 40 квартир осталось заселить.
Решение выражением:
80 – 8 · 5 = 40 (кв.), где 8 · 5 – количество квартир, которые уже заселили.
Номер 2.
Поставь вопрос так, чтобы задача решалась двумя действиями; реши задачу.
1) В школьном дворе росло 12 берез, а рябин в 4 раза меньше.
2) На первом этаже школы 9 учебных помещений, а на втором – на 2 больше.
3) На строительстве дома работали 10 плотников, а маляров в 2 раза больше.
Задача 1: Сколько деревьев росло в школьном дворе?

1) 12 : 4 = 3 (р.) – рябина.
2) 12 + 3 = 15 (д.)
Ответ: 15 деревьев росло в школьном дворе.
Задача 2:
Сколько помещений на двух этажах школы?

1) 9 + 2 = 11 (п.) – на втором этаже.
2) 9 + 11 = 20 (п.)
Ответ: 20 помещений на двух этажах.
Задача 3:
Сколько рабочих работало на стройке?

1) 10 ∙ 2 = 20 (м.) – работало на стройке. 2) 10 + 20 = 30 (р.) Ответ: 30 рабочих работало на стройке.
1) Задача 1: «в 4 раза больше», значит, вычисляется умножением «всего», значит, вычисляется сложением, знак плюс.
2)Задача 2: «на 2 помещения больше», значит, вычисляется сложением, знак плюс «всего», значит, вычисляется сложением.
3)Задача 3: «в 2 раза больше», значит, вычисляется умножением «всего», значит, вычисляется сложением.
Ставим вопрос и оформляем условие в виде краткой записи.
Сколько деревьев росло в школьном дворе?
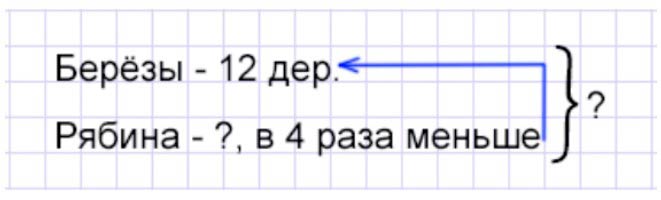
Рассуждаем.
В школьном дворе росло 12 берез, а рябин – в 4 раза меньше. Соответственно, чтобы узнать, сколько рябин росло в школьном дворе, нужно количество берез разделить на 4.
12 : 4 = 3 (дер.) – росло рябин в школьном дворе.
Продолжаем рассуждение.
Общее количество деревьев в школьном дворе складывается из количества берез и рябин, поэтому, чтобы узнать, сколько деревьев было во дворе, нужно сложить количество берез и рябин.
12 + 3 = 15 (дер.) – всего растёт в школьном дворе.
Записываем ответ.
Ответ: 15 деревьев росло в школьном дворе.
Решение выражением:
12 + 12 : 4 = 15 (дер.), где 12 : 4 – количество рябин.
Ставим вопрос и оформляем условие в виде краткой записи.
Сколько помещений на двух этажах школы?
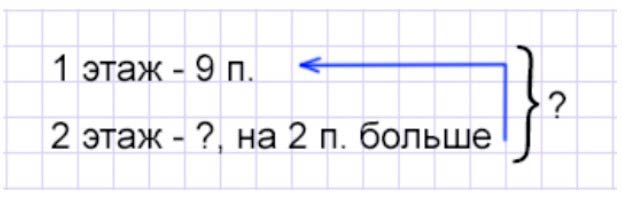
Рассуждаем.
На первом этаже школы 9 учебных помещение, а на втором – на 2 больше. Значит, что на втором этаже столько же помещений, сколько на первом и еще 2 помещения. Соответственно, чтобы узнать, сколько помещений на втором этаже, нужно к количеству помещений на первом этаже прибавить 2 помещения.
9 + 2 = 11 (уч. п.) – на втором этаже.
Продолжаем рассуждение.
Общее количество помещений складывается из количества помещений на первом и втором этаже. Значит, чтобы узнать, сколько помещений в школе, нужно сложить количество помещений на обоих этажах.
9 + 11 = 20 (п.) – помещений на двух этажах школы.
Записываем ответ.
Ответ: 20 помещений на двух этажах.
Решение выражением:
9 + (9 + 2) = 20 (п.), где 9 + 2 – количество помещений на втором этаже.
Ставим вопрос и оформляем условие в виде краткой записи.
Сколько рабочих работало на стройке?
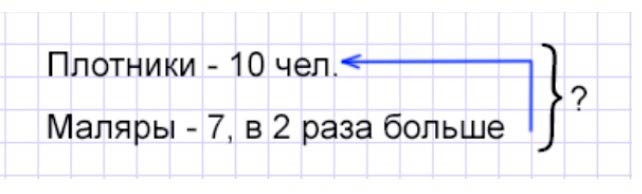
Рассуждаем.
На строительстве дома работали 10 плотников, а маляров – в 2 раза больше. Значит, чтобы узнать, сколько маляров работало на строительстве, нужно количество плотников умножить на 2.
10 ∙ 2 = 20 (м.) – работало на стройке.
Продолжаем рассуждение.
Общее количество рабочих на стройке складывается из количества маляров и плотников. Значит, чтобы узнать, сколько рабочих было на стройке, нужно сложить количество маляров и плотников.
10 + 20 = 30 (р.) – всего работало на стройке.
Записываем ответ.
Ответ: 30 рабочих работало на стройке.
Решение выражением:
10 + 10 · 2 = 30 (р.), где 10 · 2 – количество маляров.
Номер 3.
В магазин привезли фрукты в ящиках: яблоки – по 9 кг в ящике, а груши – по 8 кг в ящике. Объясни, что означают выражения:
9 + 8 9 ∙ 3 8 ∙ 4 8 ∙ 4 + 9 9 ∙ 3 + 8
Ответ:9 + 8 – столько груш и яблок в двух ящиках. 9 ∙ 3 – столько яблок в трёх ящиках. 8 ∙ 4 – столько груш в четырёх ящиках. 8 ∙ 4 + 9 – столько груш в трёх ящ., и яблок в первом ящ. 9 ∙ 3 + 8 – столько яблок в трёх ящ. и груш в первом ящике.
Данная задача: вида «вместимость 1 ящика, количество ящиков, общее количество фруктов» характеризуется зависимостями между компонентами:
Вместимость 1 ящика · количество ящиков = общее количество фруктов.
Общее количество фруктов : количество ящиков = вместимость 1 ящика.
Общее количество фруктов : вместимость 1 ящика = количество ящиков.
Оформляем условие в виде таблицы.
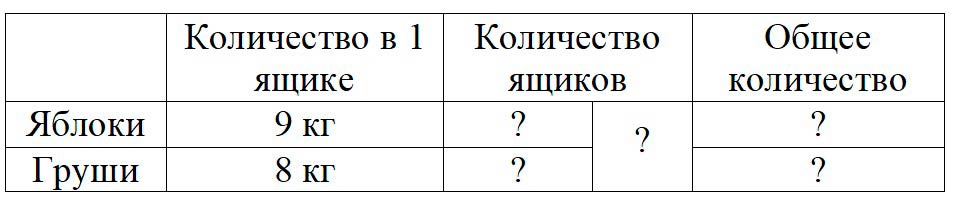
Рассуждаем.
Мы знаем, сколько фруктов в одном ящике с яблоками и в одном ящике с грушами. Но не известно какова масса этих двух ящиков.
Чтобы это узнать, нужно массу одного ящика с яблоками сложить с массой одного ящика с грушами.
9 + 8 = 17 (кг) – столько груш и яблок в двух ящиках.
Продолжаем рассуждение.
В одном ящике с яблоками содержится 9 кг фруктов, а в одном ящике с грушами – 8 кг.
Чтобы узнать какая масса фруктов в нескольких ящиках, нужно массу одного ящика умножить на количество ящиков.
9 ∙ 3 = 27 (кг) – столько яблок в трёх ящиках.
8 ∙ 4 = 32 (кг) – столько груш в четырёх ящиках.
Продолжаем рассуждение.
Мы узнали, чему равняется масса груш в 4 ящиках и знаем массу одного ящика яблок. Чтобы узнать общую массу, нужно массу 4 ящиков с грушами сложить массу одного ящика с яблоками.
8 ∙ 4 + 9 = 32 + 9 = 41 (кг) – столько груш в 4 ящиках и яблок в 1 ящике.
Продолжаем рассуждение.
Мы узнали, чему равняется масса яблок в 3 ящиках и знаем массу одного ящика груш. Чтобы узнать общую массу, нужно массу 3 ящиков с яблоками сложить массу одного ящика с грушами.
9 ∙ 3 + 8 = 27 + 8 = 35 (кг) – столько яблок в 3 ящиках и груш в 1 ящике.
Оформляем задание в тетрадь.
9 + 8 = 17 (кг) – столько груш и яблок в двух ящиках.
9 ∙ 3 = 27 (кг) – столько яблок в трёх ящиках.
8 ∙ 4 = 32 (кг) – столько груш в четырёх ящиках.
8 ∙ 4 + 9 = 41 (кг) – столько груш в 4 ящиках и яблок в первом ящике.
9 ∙ 3 + 8 = 35 (кг) – столько яблок в трёх ящиках и груш в одном ящике.
Номер 4.
Какие из чисел от 42 до 63 делятся на 7 без остатка?
Ответ:42 : 7 = 6 49 : 7 = 7 56 : 7 = 8 63 : 7 = 9 Ответ: 42, 49, 56, 63
1) Делятся без остатка на 7, значит, являются результатами таблицы умножения 7.
2) Вспомни таблицу умножения 7.
Выпишем все числа от 42 до 63.
42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63.
Выпишем числа, которые делятся на 7 без остатка.
Вспомним таблицу умножения на 7.
7 · 6 = 42
7 · 7 = 49
7 · 8 = 56
7 · 9 = 63
Данные числа – это результат умножения на 7.
Значит, выписываем числа 42, 4, 56, 63.
Номер 5.
Подбери делимое и делитель.
Ответ:
90 : 10 = 9
9 : 1 = 9
36 : 4 = 9
63 : 7 = 9
18 : 2 = 9
45 : 5 = 9
72 : 8 = 9
27 : 3 = 9
54 : 6 = 9
81 : 9 = 9
1) Вспомни названия компонентов действия деления и зависимость между компонентами и результатом действия деления:
Делимое – это то число, которе делят.
Делитель – это то число, на которое делят.
2) Нам известно значение частного – 9, значит, необходимо вспомнить таблицу умножения и деления 9:
Вспомним таблицу умножения на 9.
9 · 1 = 9
9 · 2 = 18
9 · 3 = 27
9 · 4 = 36
9 · 5 = 45
9 · 6 = 54
9 · 7 = 63
9 · 8 = 72
9 · 9 = 81
9 · 10 = 90
Рассуждаем.
9 : 1 = 9, 9 – делимое, 1 – делитель
18 : 2 = 9, 18 – делимое, 2 – делитель
27 : 3 = 9, 27 – делимое, 3 – делитель
36 : 4 = 9, 36 – делимое,42 – делитель
45 : 5 = 9, 45 – делимое, 5 – делитель
54 : 6 = 9, 54 – делимое, 6 – делитель
63 : 7 = 9, 63 – делимое, 7 – делитель
72 : 8 = 9, 72 – делимое, 8 – делитель
81 : 9 = 9, 81 – делимое, 9 – делитель
90 : 10 = 9, 90 – делимое, 10 – делитель.
Номер 6.
Ответ:9 ∙ 5 = 45 56 : 8 = 7 4 ∙ 9 = 36 54 : 9 = 6 6 ∙ 7 = 42 49 : 7 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним умножение.
9 · 5 = 45,
где 9 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним деление.
56 : 8 = 7, так как 8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
54 : 9 = 6, так как 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
49 : 7 = 7, так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Расставляем порядок действий и выполняем вычисления.
1 2
42 : 6 ∙ 9 = 63
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 42 : 6 = 7, так как 6 · 7 = 42
2) 7 ∙ 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
1 2
32 : 8 ∙ 3 = 12
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 32 : 8 = 4,так как 8 · 4 = 32
2) 4 ∙ 3 = 12,
где 4 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
1 2
27 : 3 ∙ 6 = 54
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 27 : 3 = 9, так как 3 · 9 = 27
2) 9 ∙ 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
2 1
8 ∙ (20 − 14) = 48
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
1) 20 – 14 = 6
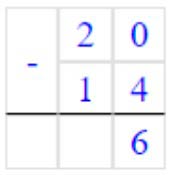
Вычитаем единицы. От числа 0 мы не можем отнять 4.
Занимаем 1 дес. = 10 ед., 10 – 4 = 6 – получилось единиц.
Записываем в разряде единиц число 6.
Вычитаем десятки. Было 2 дес., мы занимали 1 дес, осталось 2 – 1 = 1 дес.,
1 – 1 = 0 – получилось десятков.
В разряде десятков цифры нет.
Читаем ответ: 4.
2) 8 ∙ 6 = 48,
где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
1 2
(36 + 12) : 6 = 8
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – деление.
1) 36 + 12 = 48
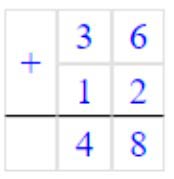
Складываем единицы. 6 + 2 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Складываем десятки. 3 + 1 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 48.
2) 48 : 6 = 8,
так как 6 · 8 = 48
1 2
(90 – 42) : 8 = 6
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 90 – 42 = 48

Вычитаем единицы. От числа 0 мы не можем отнять 2.
Занимаем 1 дес. = 10 ед., 10 – 2 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 9 дес., мы занимали 1 дес, осталось 9 – 1 = 8 дес.,
8 – 4 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 48.
2) 48 : 8 = 6, так как 8 · 6 = 48
Оформляем задание в тетрадь.
9 ∙ 5 = 45
4 ∙ 9 = 36
6 ∙ 7 = 42
56 : 8 = 7
54 : 9 = 6
49 : 7 = 7
42 : 6 · 9 = 7 · 9 = 63
32 : 8 · 3 = 4 · 3 = 12
27 : 3 · 6 = 9 · 6 = 54
8 · (20 – 14) = 8 · 6 = 48
(36 + 12) : 6 = 48 : 6 = 8
(90 – 42) : 8 = 48 : 8 = 6
Номер 7.
8 карандашей стоят 24 р.
1) Сколько стоят 7 таких карандашей?
2) Сколько таких карандашей может купить Света, если у нее только 20 р.? Сколько ей должны дать сдачи?
Задача 1:

1-й способ решения: 1) 24 : 8 = 3 (руб.) – стоит 1 карандаш. 2) 3 ∙ 7 = 21 (руб.) Ответ: 21 рубль стоят 7 карандашей.
2-й способ решения: 24 : 8 ∙ 7 = 3 ∙ 7 = 21 (руб.) – стоят 7 карандашей Ответ: 21 рубль.
Задача 2:
Было – 20 руб.
Купила – ? к. по 3 руб.
Осталось – ? руб.
20 : 3 = 6 (ост.2)
Ответ: 6 карандашей можно купить на 20 рублей, сдачу 2 рубля получит Света.
Данная задача: вида «цена карандаша, количество карандашей, общая стоимость» характеризуется зависимостями между компонентами:
Цена карандаша · количество карандашей = общая стоимость.
Общая стоимость : цена карандаша = количество карандашей.
Общая стоимость : количество карандашей = цена карандаша.
Оформляем условие в виде таблицы.
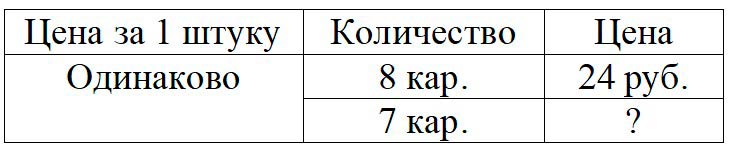
Рассуждаем.
Нам известно количество карандашей и общая стоимость всех карандашей, но неизвестно – сколько стоит 1 карандаш. Из таблицы видно, что чтобы узнать цену карандаша, нужно общую стоимость карандашей разделить на их количество.
24 : 8 = 3 (руб.) – стоит 1 карандаш.
Продолжаем рассуждение.
Нам известны, цена 1 карандаша и их количество, но неизвестно, сколько стоят 7 таких карандашей.
При этом, общая стоимость всех карандашей складывается из стоимости каждого карандаша. Значит, чтобы узнать, сколько стоят все карандаши, нужно сложить стоимости всех 7 карандашей.
Но цена одного карандаша одинаковая, значит, сложение одинаковых слагаемых можно заменить умножением.
3 ∙ 7 = 21 (руб.) – стоят 7 карандашей.
Записываем ответ.
Ответ: 21 рубль стоит 7 карандашей.
Решение выражением:
(24 : 8) · 7 = 21 (руб.), где 24 : 8 – цена 1 карандаша.
Оформляем условие в виде краткой записи.
Было – 20 руб.
Купила – ? к. по 3 руб.
Осталось – ? руб.
Рассуждаем.
Нам известны, цена 1 карандаша и сколько общее количество денег на покупку, но неизвестно, сколько можно купить карандашей и какова будет сдача.
При этом, общая стоимость всех карандашей складывается из стоимости каждого карандаша.
Но цена одного карандаша одинаковая, значит, чтобы узнать сколько можно купить карандашей нужно количество денег разделить на стоимость одного карандаша.
20 : 3 = 6 (ост.2) (кар.) – может купить Света и останется 2 рубля.
Записываем ответ.
Ответ: 6 карандашей, сдача 2 рубля.
Номер 8.
Периметр треугольника равен 48 см. Длина одной его стороны 16 см, а другой – 18 см. Найди длину третьей стороны этого треугольника.
Ответ:
1-й способ решения: 1) 16 + 18 = 34 (см) – длина двух сторон треугольника. 2) 48 − 34 = 14 (см) – длина третьей стороны треугольника. Ответ: длина третьей стороны составляет 14 см.
2-й способ решения: 1) 48 – 16 = 32 (см) – сумма длин второй и третьей стороны 2) 32 – 18 = 14 (см) – длина третьей стороны Ответ: 14 см.
3-й способ решения: 48 – 16 – 18 = 32 – 18 = 14 (см) – длина 3 стороны или 48 – (16 + 18) = 48 – 34 = 14 (см) – длина 3 стороны Ответ: 14 см.
1) Треугольник – замкнутая ломаная.
2) Решение задачи сводится к выражению, основанном на правиле вычитания суммы из числа: а – (в + с) = (а – в) – с.
Оформляем условие в виде краткой записи.
Периметр – 48 см
Длина первой стороны – 16 см
Длина второй стороны – 18 см
Длина третьей стороны – ?
Рассуждаем.
Длина ломаной – сумма длин всех отрезков-звеньев.
Треугольник – замкнутая ломаная, значит, периметр треугольника – сумма длин всех его сторон. Соответственно, чтобы узнать периметр треугольника, нужно измерить длины всех его сторон, а полученные значения сложить.
Периметр треугольника равен сумме длин всех сторон. Нам известны длины двух сторон, а третьей – нет.
Найдём сумму двух сторон треугольника.
16 + 18 = 34 (см) – сумма длин двух сторон треугольника.
Продолжаем рассуждение.
Чтобы узнать, какова длина третьей стороны, нужно из периметра треугольника вычесть сумму двух других сторон.
48 – 34 = 14 (см) – длина третьей стороны треугольника.
Записываем ответ.
Ответ: 14 см длина третьей стороны.
Рассмотрим все способы решения.
Решение задачи сводится к выражению:
48 – (16 + 18), где 16 + 18 – сумма длин двух других сторон.
Выражение основано на правиле вычитания суммы из числа. Вычислить значение данного выражения можно тремя способами, поэтому и решения задачи существует тоже три:
1 решение:
48 – (16 + 18) = 48 – 34 = 14
В первом действии вычисляю сумму длин двух известных сторон, а во втором – длину третьей стороны через вычитание из периметра суммы длин двух других сторон.
2 решение:
48 – (16 + 18) = (48 – 18) – 16 = 30 – 16 = 14
В первом действии вычисляю суммы длин второй и третьей стороны, а во втором – какова длина третьей стороны, через вычитание из суммы сторон длину второй.
3 решение:
48 – (16 + 18) = (48 – 16) – 18 = 32 – 18 = 14
В первом действии вычисляю, сколько в сумме составляют первая и третья сторона, а во втором – какова длина третьей стороны, через вычитание из суммы сторон длину первой.
Номер 9.
1) Из каких трёх фигур можно сложить прямоугольник? Запиши их номера. Найди два способа.
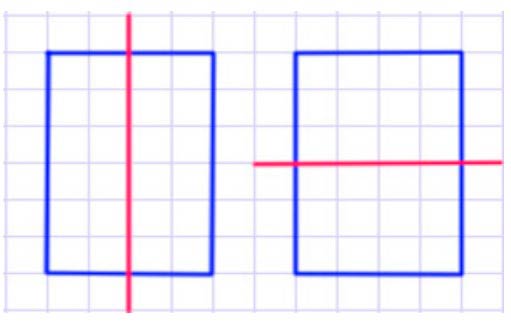
2) Начерти такой прямоугольник и проведи в нём оси симметрии.

1 способ: 1,3,4. 2 способ: 1,2,4.

Решить задачу проще, если производить реальные действия, т.е. начертить такие фигуры и вырезать их из листа клетчатой бумаги, а затем – сложить из них прямоугольник.
Составим прямоугольник разными способами.
Способ решения 1.;
Прямоугольник можно составить из фигур 1, 2, 4
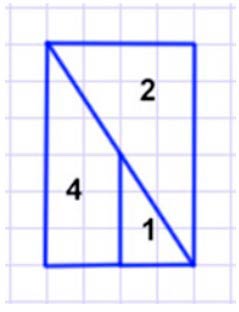
Получится пямоугольник со сторонами 2 см и 3 см.
Способ решения 2.;
Прямоугольник можно сосотавить из следующих фигур 1, 3, 4.
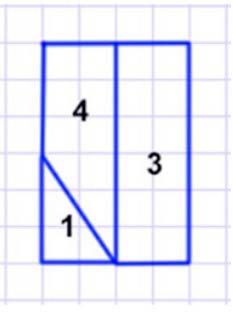
Получится пямоугольник со сторонами 2 см и 3 см.
Ось симметрии.
Ось симметрии – это линия, по которой можно сложить фигуру так, что две части при наложениисовпадут, а полощади частей будут равными.
У данной фигуры две оси симметрии:
1 ось симметрии – вертикальная.
2 ось симметрии – горизонтальная.
Номер 19.
Из 14 мотков шерсти бабушка связала носки, затратив на каждую пару по 2 мотка. Внукам она подарила 3 пары носков. Сколько ещё пар носков у неё осталось?
Ответ:Было – 14 м. Связала – ? п. по 2 м. Отдала – 3 п. Осталось – ? п. 1) 14 : 2 = 7 (п.) – носков связала бабушка. 2) 7 – 3 = 4 (п.) Ответ: 4 пары носков у неё осталось.
Данная задача: вида «расход шерсти на 1 пару, кол-во пар, общий расход шерсти» характеризуется зависимостями между компонентами:
Расход шерсти на 1 пару · кол-во пар = общий расход шерсти.
Общий расход шерсти : расход шерсти на 1 пару = кол-во пар.
Общий расход шерсти : кол-во пар = расход шерсти на 1 пару.
Оформляем условие в виде таблицы.
Из 14 мотков шерсти бабушка связала носки, затратив на каждую пару по 2 мотка. Значит, нам известен расход шерсти на 1 пару, общее количество мотков, но неизвестно – сколько пар носков было связано.
Значит, заполняю всеми имеющимися данными таблицу:
.jpg)
Рассуждаю.
Из таблицы видно, что общее количество потраченной шерсти складывается из расхода шерсти на каждую пару. Поэтому, чтобы узнать, сколько пар носков связала бабушка, нужно общее количество шерсти разделить на расход шерсти на 1 пару.
14 : 2 = 7 (п.) – носков связала бабушка.
Продолжаем рассуждение.
Мы узнали, что всего бабушка связала 7 мотков. Общее количество связанных носков складывается из количества подаренных носков и оставшихся. Поэтому, чтобы узнать, сколько носков у нее осталось, нужно из общего количество пар носков вычесть количество подаренных.
7 − 3 = 4 (п.) – носков осталось.
Записываем ответ.
Ответ: 4 пары носков осталось.
Решение выражением: 14 : 2 – 3 = 4 (п.), где 14 : 2 – количество пар носков, которые связала бабушка.
Номер 20.
Два мальчика плыли навстречу друг другу. Один проплыл до встречи 27 м, а другой – на 4 м меньше. Какое расстояние было между ними сначала? Рассмотри схематический чертёж и реши задачу.

1) 27 – 4 = 23 (м) – проплыл второй мальчик. 2) 27 + 23 = 50 (м) – расстояние между ними. Ответ: 50 метров было между мальчиками сначала.
1) «на 4 м меньше», значит, вычисляется вычитанием.
2) «всего», значит, вычисляется сложением.
Оформляем условие в виде схематического чертежа.
.jpg)
Рассуждаем.
Один пловец проплыл 27 метров, а второй – на 4 метра меньше. Значит, что второй пловец проплыл столько же, сколько первый пловец, но без 4 метров. Поэтому, чтобы узнать, сколько метров проплыл второй пловец, нужно из расстояния, которое проплыл первый пловец вычесть 4 метра.
27 − 4 = 23 (м) – проплыл второй мальчик.
Продолжаем рассуждение.
Общее расстояние, которое было между мальчиками складывается из расстояния, которое проплыл первый мальчик и второй. Значит, чтобы узнать, на каком расстоянии находились друг от друга мальчики, нужно сложить расстояния, которые проплыли оба мальчика.
27 + 23 = 50 (м) – расстояние между ними.
Записываем ответ.
Ответ: 50 метров расстояние между мальчиками.
Решение выражением: 27 + (27 – 4) = 50 (м), где 27 – 4 – расстояние, которое проплыл второй пловец.
Номер 21.
Соревновались в плавании 12 учеников, в беге на 6 учеников больше, чем в плавании, а в гимнастике в 2 раза меньше учеников, чем в беге. Сколько учеников соревновались в гимнастике?


1) 12 + 6 = 18 (уч.) – соревновались в беге. 2) 18 : 2 = 9 (уч.) Ответ: 9 учеников соревновались в гимнастике.
1) «на 6 учеников больше», значит, вычисляется сложением.
2) «в 2 раза меньше», значить, вычисляется делением.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
В плавании соревновались 12 учеников, а в беге – на 6 учеников больше. Значит, что в беге участвовали столько детей, сколько в плавании и еще 6 учеников.
Поэтому, чтобы узнать, сколько детей участвовало в беге, нужно к количеству пловцов прибавить 6 детей.
12 + 6 = 18 (уч.) – соревновались в беге.
Продолжаем рассуждение.
В соревнованиях по гимнастике участвовало в 2 раза меньше учеников, чем в беге. Соответственно, чтобы узнать, сколько детей участвовало в соревнованиях по гимнастике, нужно общее количество детей, участвовавших в беге разделить на 2.
18 : 2 = 9 (уч.) − соревновались в гимнастике.
Записываем ответ.
Ответ: 9 учеников соревновались в гимнастике.
Решение выражением: (12 + 6) : 2 = 9 (уч.), где 12 + 6 – количество участников соревнований в беге.
Номер 22.
Для школьного зала купили 50 новых стульев. 10 стульев поставили на сцену, а остальные – в зал, по 8 стульев в каждом ряду. Сколько рядов из новых стульев получилось?
Ответ:Всего – 50 ст. Сцена – 10 ст. Зал – ? р. по 8 ст. 1) 50 – 10 = 40 (ст.) – поставили в зал. 2) 40 : 8 = 5 (р.) Ответ: 5 рядов стульев было в зале.
Данная задача: вида «кол-во стульев в ряду, кол-во рядов, общее кол-во стульев» характеризуется зависимостями между компонентами:
Кол-во стульев в 1 ряду · кол-во рядов = общее кол-во стульев.
Общее кол-во стульев : кол-во стульев в 1 ряду = кол-во рядов.
Общее кол-во стульев : кол-во рядов = кол-во стульев в 1 ряду.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Для школьного зала купили 50 новых стульев. При этом общее количество стульев складывается из количества стульев, которые поставили на сцену и в зал. Поэтому, чтобы узнать, сколько стульев поставили в зал, нужно из общего количество стульев вычесть количество стульев, поставленных на сцену.
50 − 10 = 40 (ст.) – поставили в зал.
Продолжаем рассуждение.
Общее количество стульев складывается из количества стульев каждого ряда. Значит, чтобы узнать, сколько радов со стульями было, нужно общее количество стульев разделить на количество стульев в 1 ряду.
40 : 8 = 5 (р.) - стульев было в зале.
Записываем ответ.
Ответ: 5 рядов стульев было в зале.
Решение выражением: (50 – 10) : 8 = 5 (р.), где 50 – 10 – количество стульев в зале.
Номер 23.
Повар 3 дня расходовал по 9 кг крупы. После этого у него осталось 13 кг крупы. Задай во-просы, чтобы решение задачи было сначала та-ким: 9 · 3 – 13; а затем таким: 9 · 3 + 13.
Ответ:
Было – ? кг
Расходовал – 3 дн. по 9 кг
Осталось – 13 кг
На сколько кг крупы больше расходовали, чем осталось?
9 · 3 – 13 = 14 (кг)
Ответ: на 14 кг больше израсходовали крупы, чем осталось.
Сколько кг крупы было сначала?
9 · 3 + 13 = 40 (кг)
Ответ: 40 кг крупы было сначала.
Данная задача: вида «кол-во стульев в ряду, кол-во рядов, общее кол-во стульев» характеризуется зависимостями между компонентами:
Кол-во стульев в 1 ряду · кол-во рядов = общее кол-во стульев.
Общее кол-во стульев : кол-во стульев в 1 ряду = кол-во рядов.
Общее кол-во стульев : кол-во рядов = кол-во стульев в 1 ряду.
Оформляем условие в виде таблицы.
.jpg)
Задаем первый вопрос.
На сколько кг крупы больше расходовали, чем осталось?
9 · 3 – 13 = 14 (кг)
Ответ: на 14кг.
Задаем второй вопрос.
Сколько кг крупы было сначала?
9 · 3 + 13 = 40 (кг)
Ответ: 40 кг было.
Номер 24.
Реши уравнения:
56 + a = 82, 87 – c = 52.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом сложения и вычитания.
Рассмотрим уравнения.
56 + а = 82,
а – неизвестное второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
87 – с = 52,
с – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
Решаем уравнение.
56 + a = 82
a = 82 − 56
a = 26
87 − c = 52
c = 87 − 52
c = 35
Выполняем проверку.
56 + а = 82
Проверка: вместо неизвестного подставим число 26.
56 + 26 = (50 + 20) + (6 + 6) = 70 + 12 = (70 + 10) + 2 = 80 + 2 = 82
82 = 82 – верно.
87 – с = 52
Проверка: вместо неизвестного подставим число 35.
87 – 35 = (80 – 30) + (7 – 5) = 50 + 2 = 52
52 = 52 – верно.
Задание на полях страницы.


Вспомни зависимость между компонентами и результатом действия сложения и вычитания.
Рассуждаем.
Количество единиц вычитаемого неизвестно, но узнать количесвто единиц вычитаемого можно, если из единиц уменьшаемого вычесть единицы значения разности.
Из 7 нельзя вычесть 9, значит у десятков уменьшаемого занимаем единицу, тогда 1 дес. + 7 ед. = 17 ед.
17 ед. – 9 ед. = 8 ед.
В вычитаемом 8 единиц.
Продолжаем рассуждение.
Количесвто десятков уменьшаемого неизвестно, но количесвто десятков уменьшаемого можно узнать, если сложить количество десятков вычитаемого и значение разности.
Значит, 3 дес. + 5 дес. = 8 дес. и ещё 1 дес., который занимали при вычислении единиц. 8 дес. + 1 дес. = 9 дес.
В уменьшаемом 9 десятков.
Записываем ответ.
Получим равенство: 97 – 38 = 59.
Запишем равенство в столбик:
-(2023).jpg)
Рассуждаем.
В равенстве неизвестно первое слагаемое. Но известно второе слагаеоме и значение суммы. Значит, чтобы найти первое слагаемое, нужно из значение суммы вычесть второе слагаемое.
Значит, 84 – 57 = 27
Первое слагаемое – 27.
Записываем ответ.
Получим равенство: 27 + 57 = 84.
Запишем равенство в столбик:
-(2023).jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.