Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 75

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 75

Номер 5.

По прямой лесной тропинке друг за другом бегут волк, лиса и заяц. Расстояние между зайцем и волком 7 м, а между зайцем и лисой 4 м. Какое расстояние может быть между лисой и волком? Кто за кем бежит?
Звери могут бежать по тропинке в таком порядке:
Расстояние между лисой и волком будет ☐ м.
Порядок может быть и другим.
Расстояние между лисой и волком будет ☐ м.
В каком еще порядке звери могли следовать друг за другом?
Выполни чертеж в тетради и определи расстояние между лисой и волком для этого случая.

Ответ:

Расстояние между лисой и волком будет 4 + 7 = 11 м. Расстояние между лисой и волком будет 7 + 4 = 11 м. Волк – лиса – заяц. Расстояние между волком и лисой 7 − 4 = 3 м.

Подсказка:

1) Перечислим еще раз все условия:
Расстояние между зайцем и волком – 7 метров.
Расстояние между зайцем и лисой – 4 метра.

2)Порядок следования животных важен, для определения расстоянии между ними.

Рассмотрим 1 случай.

Шаг 1.
Оформляем условие в виде рисунка.

Шаг 2.
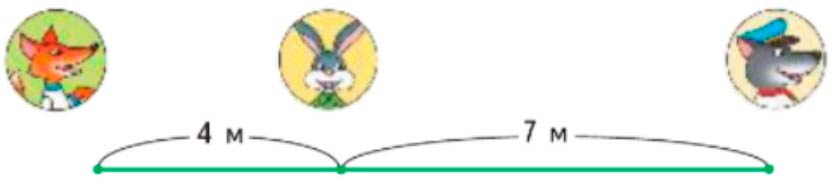
Рассуждаем.

Звери могут бежать по тропинке в таком порядке: Лиса – заяц – волк.
Рассмотяние между лисой и волком складывается из расстояний между лисой и зайцем и расстоянием между зайцем и волком.
Значит, чтобы узнать, какое расстояние между лисой и волком, нужно сложить расстояние между лисой и зайцем с расстоянием между зайцем и волком.

4 + 7 = 11 (м) – расстояние между лисой и волком.

Шаг 3.
Записываем ответ.

Ответ: расстояние между лисой и волком 11 метров.

Рассмотрим 2 случай.

Шаг 1.
Оформяляем условие в в иде рисунка.

Шаг 2.
Рассуждаем.

Звери могут бежать по тропинке в таком порядке: Волк – заяц – лиса.
Расстояние между лисой и волком складывается из расстояний между волком и зайцем и расстоянием между айцем и лисой.
Значит, чтобы узнать, какое расстояние между лисой и волком, нужно сложить расстояние между лисой и зайцем с расстоянием между зайцем и волком.

7 + 4 = 11 (м) – расстояние между лисой и волком.

Шаг 3.
Записываем ответ.

Ответ: расстояние между лисой и волком 11 метров.

Рассмотрим 3 случай.

Шаг 1.
Оформяляем условие в в иде рисунка.

Шаг 2.
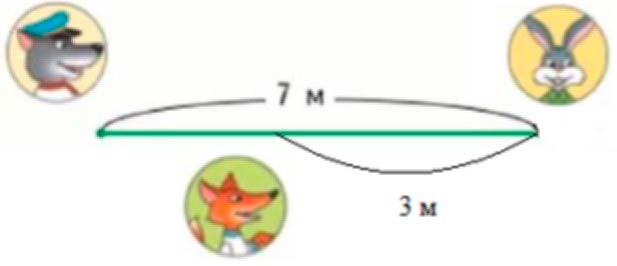
Рассуждаем.

Звери могут бежать по тропинке в таком порядке: Волк – лиса – заяц.
Расстояние между лисой и волком складывается из разницы между расстоянием волком и зайцем и расстоянием зайца и лисы.
Значит, чтобы узнать, какое расстояние между волком и лисой, нужноиз расстояния между волком и зайцем вычесть расстояние между лисой и зайцем.

7 – 4 = 3 (м) – расстояние между лисой и волком.

Шаг 3.
Записваем ответ.

Ответ: расстояние между лисой и волком 3 метра.

Номер 6.

Рассмотри рисунок.
Выбери высказывания, верные для данного рисунка.
1) Если фигура зеленого цвета, то это треугольник.
2) Все фигуры красного цвета – прямоугольники.
3) Все фигуры не красного цвета – треугольники.
Составь еще одно высказывание, верное для данного рисунка.

Ответ:

Верные: 2, 3. Синяя фигура – не прямоугольник.

Подсказка:

1) Доказывай все высказывания или опровергай их, подбирая обоснования или опровержения.

2) Помни, что фигуру называют по количество углов. Опиши сначала все, а потом узнаешь, какие высказывания верны, а какие – нет.

Шаг 1.
Рассмотрим и опишем фигуры.

Опишем все фигуры по из свойствам: количесвто углов, цвет, размер.

Фигура 1 – большой красный прямоугольник;
Фигура 2 – маленький голубой треугольник;
Фигура 3 – большой зелёный трекгольник;
Фигура 4 – большой красный четырёхугольник (квадрат).

Шаг 2.
Рассмотрим высказывания.

1) Если фигура зеленого цвета, то это треугольник – верно, так какна рисунке только она фигура зелёного цвета и это треугольник.

2) Все фигуры красного цвета − прямоугольники – верно, так как на рисунке два красных прямоугольника – под номерами 1 и 4, но фигура 4 – это квадрат, а квадрат – это прямоугольник, у которгоьо все стороны равны.

3) Все фигуры не красного цвета − треугольники – верно, так как на рисунке красных фигур две и это четырёхугольники. А треугольник цветом – голубой и зелёный.

4) Фигура красного цвета состоит из четырех сторон – верно, так как синяя фигура только олна и это четырёхугольник.

Своё высказывание:
Синяя фигура – не прямоугольник, верно, так как на рисунке только одна синяя фигура и это треугольник.

Шаг 3.
Записываем ответ.

Ответ: все высказывания верны.
Своё высказывание: синяя фигура – не прямоугольник.

математика 3 класс Моро 1 часть страница 75. Год 2023

Номер 10.

Реши уравнения, подбирая значения х.

x · 38 = 38 x · 8 = 0 26 – x = 0

Ответ:

х · 38 = 38 х = 38 : 38 х = 1 Проверка: 1 · 38 = 38 Ответ: х = 1
х · 8 = 0 х = 0 : 8 х = 0 Проверка: 0 · 8 = 0 Ответ: х = 0
26 - х = 0 х = 26 - 0 х = 26 Проверка: 26 - 26 = 0 Ответ: х = 26

Подсказка:

1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.

2) Вспомни зависимость между компонентами и результатом действия умножения и деления.

Шаг 1.
Рассмотрим уравнения.

х · 38 = 38
Данное уравнение основано на арифметическом действии умножения. Известен второй множитель и значение произведения. При этом они равны. Такое возможно только если первый множитель равен единице, потому что если 1 умножить на любое число, то получится это же число.

х · 8 = 0
Данное уравнение основано на арифметическом действии умножения. Известен второй множитель и значение произведения. При этом значение произведения равно нулю. Такое возможно, только если увеличивать ноль на любое число. Соответственно, первый множитель равен нулю.

26 – х = 0
Данное уравнение основано на арифметическом действии вычитания. Известно уменьшаемое и значение разности. При этом, значение разности равно нулю. Такое возможно, только если из числа вычитать это же число. Соответственно, вычитаемое равно уменьшаемому.

Шаг 2.
Решаем уравнение.

х · 38 = 38,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.

х · 8 = 0,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.

26 – х = 0
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 26 – 0
х = 26

Шаг 3.
Выполняем проверку.

х · 38 = 38
Проверка: вместо неизвестного подставим число 1.
1 · 38 = 38
38 = 38 – верно.

х · 8 = 0
Проверка: вместо неизвестного подставим число 0.
0 · 8 = 0
0 = 0 – верно.

26 – х = 0
Проверка: вместо неизвестного подставим число 26.
26 – 26 = 0
0 = 0 – верно.

Шаг 4.
Оформляем задание в тетрадь.

х ∙ 38 = 38
Вспомни правило умножения на 1. Если число умножить на единицу, то получится тоже самое число.
х = 1.

х ∙ 8 = 0
Если произведение равно 0, то значит один из множителей тоже равен 0.
х = 0.

26 – х = 0
Если разность равно 0, то значит уменьшаемое и вычитаемое это одно и тоже число.
х = 26.

Номер 11.

Реши уравнения.

30 + x = 56 m – 14 = 80 70 – k = 47

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 75. Номер 11

Подсказка:

Вспомни названия компонентов действия вычитания и сложения, а также зависимости между компонентами и результатами действий сложения и вычитания.

Шаг 1.
Рассмотрим уравнения.

30 + х = 56,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.

m – 14 = 80,
m – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.

70 – к = 47,
к – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.

Шаг 2.
Решаем уравнения.

30 + х = 56
х = 56 – 30
х = 26

m − 14 = 80
m = 80 + 14
m = 94

70 − k = 47
k = 70 − 47
k = 23

Шаг 3.
Выполним проверку.

30 + х = 56
Проверка: вместо неизвестного подставим число 26.
30 + 26 = 56

56 = 56 – верно.

m – 14 = 80
Проверка: вместо неизвестного подставим число 94.
94 – 14 = 80

80 = 80 – верно.

70 - k = 47
Проверка: вместо неизвестного подставим число 23.
70 – 23 = 47

47 = 47 – верно.

Шаг 4.
Оформляем задание в тетрадь.

30 + х = 56
Чтобы найти один из слагаемых, нужно из суммы вычесть второе слагаемое.
х = 56 – 30
х = 26

m − 14 = 80
Чтобы найти неизвестное уменьшаемое, нужно к разности и вычитаемое сложить.
m = 80 + 14
m = 94

70 − k = 47
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
k = 70 − 47
k = 23

Номер 12.

Сравни, не вычисляя, значения выражений.

7 · 9 ◯ 9 · 7 7 + 9 ◯ 9 + 7 38 – 4 ◯ 38 36 : 4 ◯ 36 : 6 7 · 8 ◯ 7 · 7 7 + 8 ◯ 7 + 7

Проверь себя вычислениями.

Ответ:

7 · 9 = 9 · 7 63 = 63
7 + 9 = 9 + 7 16 = 16
38 – 4 < 38 34 < 38
36 : 4 > 36 : 6 9 > 6
7 · 8 > 7 · 7 56 > 49
7 + 8 > 7 + 7 15 > 14

Подсказка:

1) Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
где а · 3,
а – первый множитель,
3 – количество множителей.
2) Помни о зависимости между компонентами и результатом действия умножения.

Шаг 1.
Рассмотрим выражения.

Рассмотрим 7 · 9 и 9 · 7
Данные выражения равны по переместительному свойству умножения, потому что от перестановки мест множителей значение произведения не изменяются.
7 · 9 = 9 · 7
Ставим знак равно.

Рассмотрим 7 + 9 и 9 + 7
Данные выражения равны по переместительному свойству сложения, потому что от перестановки мест слагаемых значение суммы не изменяется.
7 + 9 = 9 + 7
Ставим знак равно.

Рассмотрим 38 – 4 и 38
Выражение слева меньше, потому что в каждом из выражений левой и правой части есть один и тот же компонент: 38, но в левой части его уменьшают на 4 единицы, а в правой – с числом никаких действий не производят.
38 – 4 < 38
Ставим знак меньше.

Рассмотрим 36 : 4 и 36 : 6
Значение выражение слева больше, потому что в левой и правой части есть одно и то же число: 36. Но в левой части его уменьшают в 4 раза, а в правой – в 6 раз. При этом, 4 < 6, значит, значение выражения в левой части больше, чем значение выражения правой части.
36 : 4 > 36 : 6
Ставим знак больше.

Рассмотрим 7 · 8 и 7 · 7
Значение выражения слева больше, чем значение выражения справа, потому что одно и то же число в левой части повторяют 8 раз, а в правой – 7 раз.
7 · 8 > 7 · 7
Ставим знак больше.

Рассмотрим 7 + 8 и 7 + 7
Значение суммы в левой части больше, чем значение суммы в правой, потому что одно и то же число в левой части увеличивают на 8, а в правой – на 7.
7 + 8 > 7 + 7
Ставим знак больше.

Шаг 2.
Выполним проверку.

Проверим вычислением, что 7 · 9 = 9 · 7
7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 7= 63,
где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выражения равны.

Проверим вычислением, что 7 + 9 = 9 + 7

7 + 9 = 7 + (3 + 6) = (7 + 3) + 6 = 10 + 6 = 16

Представим число 9 в виде суммы чисел 3 и 6. Вначале к числу 7 прибавим число 3, а потом прибавим число 6.
9 + 7 = 9 + (1 + 6) = (9 + 1) + 6 = 10 + 6 = 16

Представим число 7 в виде суммы чисел 1 и 6. Вначале к числу 9 прибавим число 1, а потом прибавим число 6.
Выражения равны.

Проверяю вычислением, что 38 – 4 < 38

38 – 4 = (30 + 8) – 4 = 30 + (8 – 4) = 30 + 4 = 34

34 < 38
Первое выражение меньше, чем второе выражение.

Проверяю вычислением, что 36 : 4 > 36 : 6
36 : 4 = 9,
так как 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 6 = 6,
так как 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
9 > 6
Первое выражение больше, чем второе выражение.

Проверяю вычислением, что 7 · 8 > 7 · 7
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
56 > 49
Первое выражение больше, чем второе выражение.

Проверяю вычислением, что 7 + 8 > 7 + 7

7 + 8 = 7 + (3 + 5) = (7 + 3) + 5 = 10 + 5 = 15

Представим число 8 в виде суммы чисел 3 и 5. Вначале к числу 7 прибавим число 3, а потом прибавим число 5.

7 + 7 = 7+ (3 + 4) = (7 + 3) + 4 = 10 + 4 = 14

Представим число 7 в виде суммы чисел 3 и 4. Вначале к числу 7 прибавим число 3, а потом прибавим число 4.
15 > 14
Первое выражение больше, чем второе выражение.

Шаг 3.
Оформляем задание в тетрадь.

7 ∙ 9 = 9 ∙ 7 – от перемены места множителей произведение не меняется.
7 ∙ 9 = 63
9 ∙ 7 = 63

7 + 9 = 9 + 7 – от перестановки слагаемых сумма не меняется.
7 + 9 = 16
9 + 7 = 16

38 - 4 < 38 – если из числа вычесть другое число, то изначальное число уменьшиться.
38 – 4 = 34
34 < 38

36 : 4 > 36 : 6 – при одинаковом делимом, чем больше делитель, тем меньше частное, то есть если 4 < 6, то 36 : 4 > 36 : 6
36 : 4 = 9
36 : 6 = 6
9 > 6

7 ∙ 8 > 7 ∙ 7 – при одинаковом первом множителе, чем больше второй множитель, тем больше и произведение, то есть если 8 > 7, то и 7 ∙ 8 > 7 ∙ 7.
7 ∙ 8 = 56
7 ∙ 7 = 49
56 > 49

7 + 8 > 7 + 7 - при одинаковом первом слагаемом, чем больше второй слагаемое, тем больше и сумма, то есть если 8 > 7, то и 7 + 8 > 7 + 7.
7 + 8 = 15
7 + 7 = 14
15 > 14

Номер 13.

Составь верные равенства и неравенства, используя выражения:

1) 9 · 3, 30 – 6, 3 · 9, 30 – 3; 2) 6 · 9, 7 · 8, 60 – 6, 32 + 8, 9 · 6

Ответ:

1) Равенства: 9 · 3 = 3 · 9 3 · 9 = 30 – 3 9 · 3 = 30 – 3
Неравенства: 3 · 9 > 30 – 6 30 – 6 < 30 – 3 9 · 3 > 30 – 6
2) Равенства: 30 – 3 = 9 · 3 6 · 9 = 60 – 6 60 – 6 = 9 · 6
Неравенства: 7 · 8 > 32 + 8 32 + 8 < 9 · 6 32 + 8 < 60 – 6

Подсказка:

1) Прежде, чем составлять верные равенства и неравенства, вычисли значение каждого выражения.

2) Равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знака равно.

3) равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знаков больше или меньше.

Задание 1.

Шаг 1.
Вычислим значения выражений.

9 · 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
30 – 6 = 24

Вычитаем единицы. От числа 0 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 – 6 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 2 дес.,
Записываем в разряде десятков число 2.
Читаем ответ: 24.

3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
30 – 3 = 27

Вычитаем единицы. От числа 0 мы не можем отнять 3.
Занимаем 1 дес. = 10 ед., 10 - 3 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 72 дес.,
Записываем в разряде десятков число 2.
Читаем ответ: 27.

Шаг 2.
Составим равенства и неравенства.

Равенства:
9 ∙ 3 = 3 ∙ 9
3 ∙ 9 = 30 – 3
9 ∙ 3 = 30 − 3

Неравенства:
3 ∙ 9 > 30 – 6
30 − 6 < 30 − 3
9 ∙ 3 > 30 – 6

Задание 2.

Шаг 1.
Вычислим значения выражений.

6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

60 – 6 = 54

Вычитаем единицы. От числа 0 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 – 6 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. Было 6 дес., мы занимали 1 дес, осталось 6 – 1 = 5 дес.,
Записываем в разряде десятков число 5.
Читаем ответ: 54.

32 + 8 = 40

Складываем единицы. 2 + 8 = 10 – получилось 1 дес. и 0 ед.
Записываем в разряде единиц число 0, а 1 дес. запоминаем.
Складываем десятки. 1 дес. мы запомнили, занчит 3 + 1 = 4 – получилось десяток.
Записываем в разряде десятков число 4.
Читаем ответ: 40.

9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

Шаг 2.
Составим равенства и неравенства.

Равенства:
30 − 3 = 9 ∙ 3
6 ∙ 9 = 60 − 6
60 − 6 = 9 ∙ 6

Неравенства:
7 ∙ 8 > 32 + 8
32 + 8 < 9 ∙ 6
32 + 8 < 60 – 6

Номер 14.

8 · 7 15 : 3 63 : 9 · 3 85 – (46 + 18) 7 · 9 54 : 9 20 : 4 · 8 27 + (40 – 12) 8 · 6 14 : 2 49 : 7 · 4 94 – (39 + 17)

Ответ:

8 · 7 = 56 15 : 3 = 5 7 · 9 = 63 54 : 9 = 6 8 · 6 = 48 14 : 2 = 7

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 75. Номер 14

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.

4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.

Шаг 1.
Выполним умножение.

8 · 7 = 56, где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

8 · 6 = 48, где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

Шаг 2.
Выполним деление.

15 : 3 = 5, так как 3 · 5 = 15, где 3 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

54 : 9 = 6, так как 9 · 6 = 54, где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

14 : 2 = 7, так как 2 · 7 = 14, где 2 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

Шаг 3.
Расставляем порядок действий и выполняем вычисления.

1 2
63 : 9 · 3 = 21
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 63 : 9 = 7, так ка 9 · 7 = 63
2) 7 ∙ 3 = 21

1 2
20 : 4 ∙ 8 = 40
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 20 : 4 = 5, так как 4 · 5 = 20
2) 5 ∙ 8 = 40

1 2
49 : 7 ∙ 4 = 28
В данном выражении присутствуют действия умножение и деление – они равносильны. Значит, выполняем действия по порядку слева направо.
1) 49 : 7 = 7, так как 7 · 7 = 49
2) 7 ∙ 4 = 28

2 1
85 − (46 + 18) = 21
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – вычитание.
1) 46 + 18 = 64

Складываем единицы. 6 + 8 = 14 – получилось 1 дес. и 4 ед.
Записываем в разряде единиц число 4, а 1 дес. запоминаем.
Складываем десятки. 4 + 1 = 5 и ещё 1 дес., который запомнили 5 + 1 = 6 – получилось десяток.
Записываем в разряде десятков число 6.
Читаем ответ: 64.

2) 85 − 64 = 21

Вычитаем единицы. 5 - 4 = 1 – получилось единиц.
Записываем в разряде единиц число 1.
Вычитаем десятки. 8 - 6 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 21.

2 1
27 + (40 − 12) = 55
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – сложение.
1) 40 – 12 = 28

Вычитаем единицы. От числа 0 мы не можем отнять 2.
Занимаем 1 дес. = 10 ед., 10 – 2 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 4 дес., мы занимали 1 дес, осталось 4 – 1 = 3 дес.,
3 – 1 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 28.

2) 27 + 28 = 55

Складываем единицы. 7 + 8 = 15 – получилось 1 дес. и 5 ед.
Записываем в разряде единиц число 5, а 1 дес. запоминаем.
Складываем десятки. 2 + 2 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 55.

2 1
94 − (39 + 17) = 38
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – вычитание.

1) 39 + 17 = 56

Складываем единицы. 9 + 7 = 16 – получилось 1 дес. и 6 ед.
Записываем в разряде единиц число 6, а 1 дес. запоминаем.
Складываем десятки. 3 + 1 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 56.

2) 94 − 56 = 38

Вычитаем единицы. От числа 4 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 + 4 = 14 ед., 14 – 6 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 9 дес., мы занимали 1 дес, осталось 9 – 1 = 8 дес.,
8 – 5 = 3 – получилось десятков.
Записываем в разряде десятков число 3.
Читаем ответ: 38.

Шаг 4.
Оформляем задание в тетрадь.

8 ∙ 7 = 56
7 ∙ 9 = 63
8 ∙ 6 = 48

15 : 3 = 5
54 : 9 = 6
14 : 2 = 7

63 : 9 · 3 = 7 · 3 = 21
20 : 4 · 8 = 5 · 8 = 40
49 : 7 · 4 = 7 · 4 = 28

85 – (46 + 18) = 85 – 64 = 21
27 + (40 – 12) = 27 + 23 = 50
94 – (39 + 17) = 94 – 56 = 38

Номер 15.

1) Какие из чисел от 18 до 81 делятся на 9? 2) Какие из чисел: 16, 24, 32 – делятся без остатка на 4? на 3? на 8? на 6? 3) Запиши три числа, которые делятся и на 2, и на 3. Проверь, делятся ли эти числа на 6.

Ответ:

1) 18, 27, 36, 45, 54, 63, 72, 81. 2) на 4 : 16, 24, 32; на 8 : 16, 24, 32; на 3 : 24; на 6 : 24. 3) на 2 и на 3 : 6, 12, 18, 6 : 6 = 1, 12 : 6 = 2, 18 : 6 = 3

Подсказка:

1) Делятся на 9, т.е. являются результатом таблицы умножения 9.
2) Без остатка на 4, 3, 8, 6, т.е. делятся нацело.
3) Делятся и на 2 и на 3, т.е. одновременно, в одно и то же время.

Шаг 1.
Рассмотрим задание 1.

Вспомним таблицу умножения на 9.
Результат умножения на 9 и есть числа, которые делятся на 9 без остатка.

Значит, выписываю числа: 18, 27, 36, 45, 54, 63, 72, 81.

Шаг 2.
Рассмотрим задание 2.

Числа, которые делятся без остатка на 4:

16 : 4 = 4, так как 4 · 4 = 16, где 4 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

24 : 4 = 6, так как 4 · 6 = 24, где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

32 : 4 = 8, так как 4 · 8 = 32, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

Числа, которые делятся без остатка на 3:

16 : 3 – не делится, так как нет такого числа, которое при умножении на 3 дал бы результат 16.

24 : 3 = 8, так как 3 · 8 = 24, где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

32 : 3 – не делится, так как нет такого числа, которое при умножении на 3 дал бы результат 32.

Числа, которые делятся без остатка на 8:

16 : 8 = 2, так как 8 · 2 = 16, где 8 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.

24 : 8 = 3, так как 8 · 3 = 24, где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.

32 : 8 = 4,так как 8 · 4 = 32, где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

Числа, которые делятся без остатка на 6:

16 : 6 – не делится, так как нет такого числа, которое при умножении на 6 дал бы результат 16.

24 : 6 = 4, так как 6 · 4 = 24, где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

32 : 6 – не делится,так как нет такого числа, которое при умножении на 6 дал бы результат 32.

Шаг 3.
Рассмотрим задание 3.

Рассмотрим числа, которые делятся на 2:
2, 4, 6, 8, 10, 12, 14, 16, 18.

Рассмотрим числа, которые делятся на 3:
3, 6, 9, 12, 15, 18, 21.

Числа, которые будут делится и на 2 и на 3:
6, 12, 18.

Числа, которые делятся и на и на 3, так же будут делится и на 6.

6 : 6 = 1, так как 6 · 1 = 6
12 : 6 = 2, так как 6 · 2 = 12
18 : 6 = 3, так как 6 · 3 = 18

Шаг 4.
Оформляем задание в тетрадь.

1) на 9 делятся: 18, 27, 36, 45, 54, 63, 72, 81.
18 : 9 = 2
27 : 9 = 3
36 : 9 = 4
45 : 9 = 5
54 : 9 = 6
63 : 9 = 7
72 : 9 = 8
81 : 9 = 9

2) на 4 делятся: 16, 24, 32.
16 : 4 = 4
24 : 4 = 6
32 : 4 = 8
на 3 делятся: 24
24 : 3 = 8
на 8 делятся: 16, 24, 32.
16 : 8 = 2
24 : 8 = 3
32 : 8 = 4
на 6 делится: 24
24 : 6 = 4

3) если число делится на 2 и на 3, значит оно делится на 6.
на 2 и на 3 делятся числа 6, 12, 18.
6 : 6 = 1
12 : 6 = 2
18 : 6 = 3

Номер 16.

9 одинаковых блокнотов стоят 72 р.

1) Сколь ко стоят 7 таких блокнотов? 4 блокнота? 2) Сколько таких блокнотов можно купить на 40 р.? на 64 р.?

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 75. Номер 16

1) 72 : 9 = 8 (р.) – стоит 1 блокнот. 2) 8 · 7 = 56 (р.) – стоит 7 блокнотов. 3) 8 · 4 = 32 (р.) – стоит 4 блокнота. 4) 40 : 8 = 5 (б.) – можно купить на 40 рублей 5) 64 : 8 = 8 (б.) – можно купить на 64 рубля Ответ: 56 рублей нужно на 7 блокнотов и 32 рубля на 4 блокнота; 5 блокнотов можно купить на 40 рублей и 8 блокнотов на 64 рубля.

Подсказка:

Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:

Цена блокнота · количество блокнотов = общая стоимость блокнотов.
Общая стоимость блокнотов : цена блокнота = количество блокнотов.
Общая стоимость блокнотов : количество блокнотов = цена блокнота.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Из таблицы видно, что цена блокнота одинаковая. А чтобы узнать сколько стоит 1 блокнот, нужно общую стоимость блокнота разделить на количество блокнотов.

72 : 9 = 8 (р.) – стоит один блокнот.

Шаг 3.
Решаем первую часть задачи.

Общая стоимость всех блокнотов складывается из стоимости каждого из семи блокнотов. Значит, чтобы узнать, сколько стоит 7 блокнотов, нужно сложить стоимости всех блокнотов.
Но цена блокнота одинаковая, поэтому сложением одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько стоят все блокноты вместе, нужно цену блокнота умножить на количество.

8 ∙ 7 = 56 (р.) – стоит 7 блокнотов.

Шаг 4.
Рассуждаемю.

Чтобы узнать, сколько стоит 4 блокнота, нужно сложить стоимости всех блокнотов.
Но цена блокнота одинаковая, поэтому сложением одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько стоят все блокноты вместе, нужно цену блокнота умножить на количество.

8 ∙ 4 = 32 (р.) – стоят 4 блокнота.

Шаг 5.
Решаем вторую часть задачи.

Общая стоимость всех блокнота складывается из стоимостей каждого из блокнотов. Поэтому, чтобы узнать, сколько блокнотов купили, нужно общую стоимость блокнотов разделить на цену блокнота.

40 : 8 = 5 (б.) – можно купить на 40 рублей.

Шаг 6.
Рассуждаем.

Общая стоимость всех блокнота складывается из стоимостей каждого из блокнотов. Поэтому, чтобы узнать, сколько блокнотов купили, нужно общую стоимость блокнотов разделить на цену блокнота.

64 : 8 = 8 (б.) – можно купить на 64 рубля.

Шаг 7.
Оформляем решение по действиям.

1) 72 : 9 = 8 (р.) – стоит один блокнот.
2) 8 ∙ 7 = 56 (р.) – стоит 7 блокнотов.
3) 8 ∙ 4 = 32 (р.) – стоят 4 блокнота.
4) 40 : 8 = 5 (б.) – можно купить на 40 рублей.
5) 64 : 8 = 8 (б.) – можно купить на 64 рубля.

Шаг 8.
Записываем ответ.

Ответ: 56 рублей и 32 рубля; 5 блокнотов и 8 блокнотов.

Номер 17.

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 75. Номер 17

1) 15 : 5 = 3 (м) – одна занавеска. 2) 21 : 3 = 7 (з.) – можно сшить из 21 м тюля. 3) 9 · 3 = 27 (м) – тюли понадобиться для 9 занавесок. Ответ: 7 занавесок можно сшить из 21 метра тюля; 27 м тюля нужно на пошив 9 занавесок.

Подсказка:

Данная задача: вида «расход на 1 занавеску, количество занавесок, общее количество тюля» характеризуется зависимостями между компонентами:

Расход на 1 занавеску · кол-во занавесок = общее кол-во тюля.
Общее кол-во тюля : кол-во занавесок = расход на 1 занавеску.
Общее кол-во тюля : расход на 1 занавеску = кол-во занавесок.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Из таблицы видно, что общее количество ткани складывается из суммы ткани, расходуемой на каждую занавеску. Значит, чтобы узнать расход на 1 занавеску, нужно общее количество ткани разделить на количество занавесок.

15 : 5 = 3 (м) – пойдёт на одну занавеску.

Шаг 3.
Продолжаем рассуждение.

Мы узнали, что расход ткани на 1 занавеску равно 3 м. Теперь нам известно общее количество ткани. Значит, нам известен расход ткани на 1 занавеску, общее количество ткани, но неизвестно, сколько таких занавесок сшили.
Чтобы узнать, сколько занавесок сшили, нужно общее количество ткани разделить на расход ткани на 1 занавеску.

21 : 3 = 7 (з.) – можно сшить из 21 м тюля.

Шаг 4.
Продолжаем рассуждение.

Из таблицы видно, что общее количество ткани складывается из количества ткани, расходуемое на пошив каждой из 9 занавесок. Значит, чтобы узнать общее количество ткани, нужно расход ткани на каждую занавеску сложить.
Но количество ткани, расходуемое на 1 занавеску одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением.

9 ∙ 3 = 27 (м) – тюли понадобиться для 9 занавесок.

Шаг 5.
Записываем ответ.

Ответ: 7 занавесок; 27 м тюля.

Номер 18.

Из каких трёх фигур можно сложить треугольник? Запиши их номера. Начерти и вырежи такой треугольник. Как показать, что этот треугольник – симметричная фигура?

Ответ:

Из фигур №1, №2, №3.

Подсказка:

Решить задачу проще, если производить реальные действия, т.е. начертить такие фигуры и вырезать их из листа клетчатой бумаги, а затем – сложить из них прямоугольник.

Шаг 1.
Составим треугольник двумя способами.