Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 66

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 66

Номер 1.

На чертеже изображен 1 дм², который разбит на квадратные сантиметры. Объясни, как подсчитать, сколько квадратных сантиметров содержится в квадратном дециметре.

Ответ:

1-й способ решения: Сторона квадрата равна 10 см, а площадь квадрата равна произведению его сторон: 10 ∙ 10 = 100 см² Тогда, 1 дм² = 100 см² Таким образом в квадратном дециметре содержится 100 квадратных сантиметров.

2-й способ решения: Посчитай количество квадратов – 100. Значит 1 дм² = 100 см²

Подсказка:

1) 1 дм² – это еще одна единица измерения площади.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Шаг 1.
Рассмотрим 1 способ решения.

Рассмотрим квадрат 1 дм², который разбит на квадратные сантиметры.
Стороны квадрата равны, в них укладывается 10 квадратов со стороной 1 см, значит, сторона большого квадрата – 10 см, т.е. 1 дм, потому что 10 см = 1 дм.

Выходит, что площадь большого квадрата со стороной 10 см равна 100 см², потому что:
а · а = 10 см · 10 см = 100 см².

И 100 см² = 1 дм², ведь стороны 10 см = 1 дм.

Шаг 2.
Рассмотрим 2 способ решения.

Мы знаем, что площадь квадрата равна 1 дм² и он разбит на квадраты со стороной 1 см. Значит площадь маленького квадрата равна:
1 см · 1 см = 1 см²

Чтобы узнать площадь квадрата в см² можно посчитать количество квадратов из которых он состоит.
Их количество – 100.

Значит, площадь квадрата равна 100 см².
Значит, 1 дм² = 100 см²

Шаг 3.
Записываем ответ.

Ответ: 1 дм² = 100 ².

Номер 2.

На обороте обложки учебника изображен квадрат площадью 1дм². Красными линиями выделены два прямоугольника. Найди площадь каждого из них.

Ответ:

1) 5 ∙ 5 = 25 см² 2) 6 ∙ 8 = 48 см² Ответ: площадь первого прямоугольника 25 см², площадь второго прямоугольника 48 см².

Подсказка:

Площадь фигуры измеряется в квадратных единицах.

Шаг 1.
Рассмотрим первый прямоугольник.

Квадрат со сторой 1 дм² разбит на 100 квадратов со стороной 1 см, так как 10 см = 1 дм.

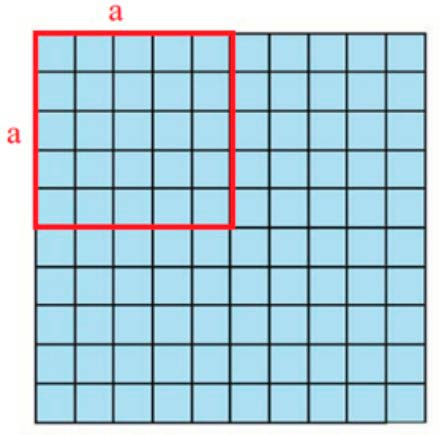
Первый прямоугольник состоит из 5 квадратов в 1 см в длину и из 5 квадратов в 1 см в ширину. Значит это фигура квадрат со стороной 5 см.

Чтобы вычислить площадь, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).

Длина и ширина у квадрата одинакова и равна 5 см.
5 см · 5 см = 25 см² – площадь квадрата со сторной 5 см.
Проверить это можно если сосчитаем количесвто клеток – их 25.

Шаг 2.
Рассмотрим второй пярмоугольник.

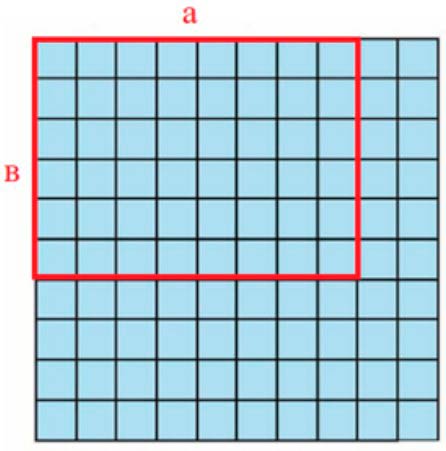
Первый прямоугольник состоит из 8 квадратов в 1 см в длину и из 6 квадратов в 1 см в ширину. Значит это прмяоугльник со сторонами 8 см и 6 см.

У прямоугольника длина равна 8 см, а ширина равна 6 см.
8 см · 6 см = 48 см² – площадь прямоугольника со сторнами 8 см и 6 см.
Проверить это можно если сосчитаем количесвто клеток – их 48.

Шаг 3.
Оформляем задание в тетрадь.

Первый прямоугольник состоит из 5 квадратов в 1 см в длину и из 5 квадратов в 1 см в ширину. Это фигура квадрат.

5 ∙ 5 = 25 (см²) − площадь первого прямоугольника (квадрата).

Второй прямоугольник состоит из 8 квадратов в 1 см в длину и из 6 квадратов в 1 см в ширину.
6 ∙ 8 = 48 (см²) − площадь второго прямоугольника.

Ответ: площадь первого прямоугольника – 25 см² второго – 48 см².

Номер 3.

Высота зеркала прямоугольной формы 10 дм, а ширина 5 дм. Чему равна площадь зеркала?

Ответ:

а = 10 дм b = 5 дм S = ? дм² S = a ∙ b S = 10 ∙ 5 S = 50 дм² Ответ: Площадь зеркала составляет 50 дм².

Подсказка:

1) Площадь фигуры измеряется в квадратных единицах.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Шаг 1.
Оформляем условие в виде краткой записи.

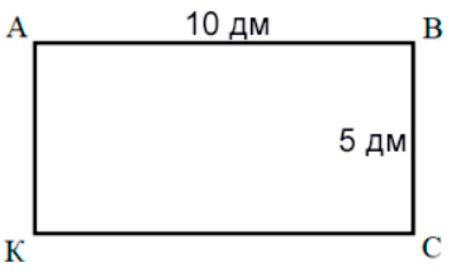
Длина – 10 дм
Ширина – 5 дм
Площадь – ?

Шаг 2.
Рассуждаем.

Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).

Дина равна 10 дм, а ширина равна 5 дм.

10 дм · 5 дм = (5 · 10) дм² = 50 дм² – площадь зеркала.

Шаг 3.
Записываем ответ.

Ответ: площадь зеркала 50 дм².

Задание на полях страницы

Занимательные рамки:

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 66, задание внизу страницы

Проверка:
Первая занимательная рамка:
14 + 15 + 7 = 21 + 15 = 36
7 + 11 + 18 = 18 + 18 = 36
14 + 4 + 18 = 18 + 18 = 36

Вторая занимательная рамка:
18 + 4 + 50 = 22 + 50 = 72
18 + 44 + 10 = 28 + 44 = 72
10 = 12 + 50 = 22 + 50 = 72

Подсказка:

Занимательные рамки – рамки, в которых числа, стоящие на одной прямой, образуют в сумме число, записанное в центре рамки.

Рассмотрим рамку 1.

Шаг 1.
Рассуждаем.

Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – это число 36.

Шаг 2.
Находим неизвестные числа.

14 + 15 + 7 = 29 + 7 = 36
14 + 4 + 18 = 18 + 18 = 36
7 + 11 + 18 = 36

Шаг 3.
Заполняем рамку числами.

Рассмотрим рамку 2.

Шаг 1.
Рассуждаем.

Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – этот число 72.

18 + 44 + 10 = 62 + 10 = 72
18 + 4 + 50 = 68 + 4 = 72
10 + 12 + 50 = 60 + 12 = 72

Шаг 2.
Заполняем рамку числами.

математика 3 класс Моро 1 часть страница 66. Год 2023

Узнаем новую единицу площади — квадратный метр.

Площадь квадрата, сторона которого 1 м, — это единица площади — квадратный метр. Слова «квадратный метр» при числах записывают так: 8 м², 20 м².
Этой единицей пользуются, например, при измерении площади комнаты, дома, сада.

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 66. Recomended-block

Номер 1.

Измерь длину и ширину класса. Узнай площадь класса в квадратных метрах.

Ответ:

Длина класса 8 м Ширина класса 4 м Вычисляю площадь класса:8 · 4 = 32 м² Ответ: площадь класса равна 32 м².

Подсказка:

1) 1 м² – это еще одна единица измерения площади.

2) Классная комната может иметь форму квадрата или прямоугольника.

3) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

4) Измерь длину и ширину класса с помощью рулетки.

Шаг 1.
Измерим ширину и длину классаю

Мы Вам представляем возможное решение данного задания.

Длина класса – 8 м
Ширина класса – 4 м

Значит класс имеет форму прямоугольника со сторонами 8 м и 4 м.

Шаг 2.
Вычислим площадь.

Номер 2.

1) Большие площади комнат, квартир, домов, земельных участков, городов и т. п. на бумаге изображают в уменьшенном виде. Например, на рисунке изображён план дачного участка, на котором за 1 м² условно принята одна клетка. Площадь дома на плане 42 клетки, значит, настоящая его площадь 42 м².
2) Найди по плану площадь сада.

Ответ:

9 · 5 = 45 м² Ответ: площадь сада 45 м².

Подсказка:

1) 1 м² – это еще одна единица измерения площади.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Шаг 1.
Рассмотрим рисунок.

На рисунке изображён план дачного участка. Нам нужно найти площадь сада.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Чтобы это сделать найдём длину и ширину сада на плане и на мместности.

Длина сада на плане равна 9 клеток, так как 1 клетка на плане равна 1 м на местности, значит:
9 · 1 м = 9 м – длина сада на местности.
Ширина сада на плане равна 5 клеток, так как 1 клетка на лпане равна 1 м на местности, значит:
5 · 1 м = 5 м – ширина сада на местности.

Шаг 2.
Найдём площадь сада.

Шаг 3.
Запишем ответ.

Ответ: площадь сада 45 м².

Номер 3.

Ответ:

Подсказка:

1) 9 · с, значит, число 9 умножить на с, т.е. увеличить в с раз.

2) а : 8, значит, число а разделить на 8, т.е. уменьшить число в 8 раз.

Таблица 1.

Шаг 1.
Промежуточные вычисления.

Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.

9 · с, если:

с = 9, то 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

с = 8, то 9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

с = 7, то 9 · 7 = 63,
где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

с = 6, то 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

с = 5, то 9 · 5 = 45,
где 9 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

Шаг 2.
Заполним таблицу.

Таблица 2.

Шаг 1.
Промежуточные вычисления.

а : 8 , если:

а = 64, то 64 : 8 = 8, так как 8 · 8 = 64,

где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

а = 56, то 56 : 8 = 7, так как 8 · 7 = 56,

где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

а = 48, то 48 : 8 = 6, так как 8 · 6 = 48,

где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

а = 40, то 40 : 8 = 5, так как 8 · 5 = 40,

где 8 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

а = 32, то 32 : 8 = 4, так как 8 · 4 = 32,

где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

Шаг 2.
Заполним таблицу.

Конец страницы

Переход на другие страницы

Содержание

Информация на этой странице была полезной?

★★★★★

0/5 (0 голосов)

Нашли ошибку на сайте? Помогите нам ее исправить!

Сообщить об ошибке

С подпиской рекламы не будет

Подключите премиум подписку со скидкой в 40% за 149 ₽

Подключить