Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 63

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
У Сережи 5 монет по 10 к., а у Володи одна монета – 50 к.
1) Поставь вопрос, чтобы задача решалась так: 10 ∙ 5 + 50.
2) Поставь к тому же условию другой вопрос, чтобы задача решалась так: 10 ∙ 5 − 50.
Задача 1:
Сколько всего денег у Серёжи и Володи?
10 ∙ 5 + 50 = 100 (к.)
100 копеек = 1 рубль
Ответ: у мальчиков 1 рубль.
Задача 2:
На сколько денег у Сережи больше, чем у Володи?
10 ∙ 5 − 50 = 0 (к.)
Ответ: у них денег поровну.
Задача 1:
Вопрос: Сколько всего денег у Серёжи и Володи?
Задача 2:
Вопрос: На сколько денег у Сережи больше, чем у Володи?
Оформляем условие в виде краткой записи.
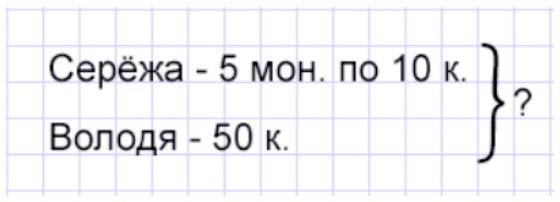
Рассуждаем.
У Серёжи 5 монет по 10 копеек. Общее количество денег у него складывается из количества денег в каждой монете. Поэтому, чтобы узнать, сколько денег у Серёжи, нужно сложить количество денег в каждой монете. Вычисляется сложением.
Но количество денег в одной монете одинаковое, значит, все монеты равны. Поэтому, сложение одинаковых слагаемых можно заменить умножением.
10 · 5 = 50 (к.) – денег у Серёжи.
Продолжаем рассуждение.
Общее количество денег складывается из денег Сережи и Володи, значит, чтобы узнать, сколько денег было у мальчиков всего, нужно сложить количества денег обоих.
50 + 50 = 100 (к.) = 1 руб. – всего денег.
Записываем ответ.
Ответ: у мальчиков 1 рубль.
Решение выражением: 10 · 5 + 50 = 100 (к.) = 1 руб.,
где 10 · 5 – количество денег Сережи.
Оформляем условие в виде краткой записи.

Рассуждаем.
У Серёжи 5 монет по 10 копеек. Общее количество денег у него складывается из количества денег в каждой монете. Поэтому, чтобы узнать, сколько денег у Серёжи, нужно сложить количество денег в каждой монете. Вычисляется сложением.
Но количество денег в одной монете одинаковое, значит, все монеты равны. Поэтому, сложение одинаковых слагаемых можно заменить умножением. 10
10 · 5 = 50 (к.) – денег у Серёжи.
Продолжаем рассуждение.
Теперь мы знаем сколько денег у обоих мальчиков. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. То есть, чтобы узнать, на сколько денег у одного мальчика больше, чем у другого, нужно из количества денег Сережи вычесть количество денег Володи.
50 – 50 = 0 (к.) – денег поровну.
Записываем ответ.
Ответ: у них денег поровну.
Решение выражением: 10 · 5 – 50 = 0 (к.),
где 10 · 5 – количество денег Сережи.
Номер 2.
Ответ:9 ∙ 4 = 36 6 ∙ 3 = 18 7 ∙ 8 = 56 1 ∙ 3 = 3 8 ∙ 9 = 72 0 ∙ 3 = 0

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Вычислим умножение:
9 · 4 = 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
Расставляем порядок действий и выполняем вычисления.
1 2
56 : 8 · 5 = 35
В выражении присутствуют действия умножение и деление – они равноправны. Поэтому выполняем действия по порядку слева направо.
1) 56 : 8 = 7, так как 8 · 7 = 56
2) 7 ∙ 5 = 35
1 2
64 : 8 ∙ 7 = 56
В выражении присутствуют действия умножение и деление – они равноправны. Поэтому выполняем действия по порядку слева направо.
1) 64 : 8 = 8, так как 8 · 8 = 56
2) 8 ∙ 7 = 56
1 2
42 : 7 ∙ 8 = 48
В выражении присутствуют действия умножение и деление – они равноправны. Поэтому выполняем действия по порядку слева направо.
1) 42 : 7 = 6, так как 6 · 7 = 42
2) 6 ∙ 8 = 48
2 1
91 − (6 + 85) = 0
В выражении присутствуют действия сложение и вычитание, а также скобки. Вначале выполняем действие в скобках – сложение, а потом вне скобок – вычитание.
1) 6 + 85 = (1 + 5) + 85 = 1 + (5 + 85) = 1 + 90 = 91
Представим число 6 в виде суммы чисел 1 и 5. Вначале к числу 85 прибавим число 5, а потом прибавим число 1.
2) 91 − 91 = 0
Если из числа вычесть само число, то получится нуль.
1 2
55 + 8 − 29 = 34
В выражении присутствуют действия сложение и вычитание – они равноправны. Поэтому выполняем действия по порядку слева направо.
1) 55 + 8 = 55 + (5 + 3) = (55 + 5) + 3 = 60 + 3 = 63
Представим число 8 в виде суммы чисел 5 и 3. Вначале к числу 55 прибавим число 5, а потом прибавим число 3.
2) 63 − 29 = 63 – (23 + 6) = (63 – 23) – 6 = 40 – 6 = 34
Число 29 представим в виде суммы чисел 23 и 6. Из числа 63 вначале вычтем число 23, а потом вычтем число 6.
1 2
41 − 5 + 36 = 72
В выражении присутствуют действия сложение и вычитание – они равноправны. Поэтому выполняем действия по порядку слева направо.
1) 41 – 5 = 41 – (1 + 4) = (41 – 1) – 4 = 40 – 4 = 36
Представим число 5 в виде суммы чисел 1 и 4. Вначале из числа 41 вычтем число 1, а потом вычтем число 4.
2) 36 + 36 = 36 + (4 + 32) = (36 + 4) + 32 = 40 + 32 = 72
Представим число 36 в виде суммы чисел 4 и 32. Вначале к числу 36 прибавим число 4, а потом число 32.
Вычислим умножение.
6 ∙ 3 = 18
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
1 ∙ 3 = 3
Если число умножить на 1, то оно не изменится.
0 ∙ 3 = 0
Если число умножить на нуль, то получится нуль.
Оформляем задание в тетрадь.
9 ∙ 4 = 36
7 ∙ 8 = 56
8 ∙ 9 = 72
56 : 8 · 5 = 7 · 5 = 35
64 : 8 · 7 = 8 · 7 = 56
42 : 7 · 8 = 6 · 8 = 48
91 – (6 + 85) = 91 – 91 = 0
55 + 8 – 29 = 63 – 29 = 34
41 – 5 + 36 = 36 + 36 = 72
6 · 3 = 18
1 · 3 = 3
0 · 3 = 0
Номер 3.
Заполни таблицу и расскажи, как при одном и том же делимом менялся делитель и как - частное.
Ответ:
Вспомни названия компонентов действий деления, а также – зависимости между компонентами и результатом действий деления.
Промежуточные вычисления.
Чтобы найти частное нужно делимое разделить на делитель.
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Заполним таблицу.
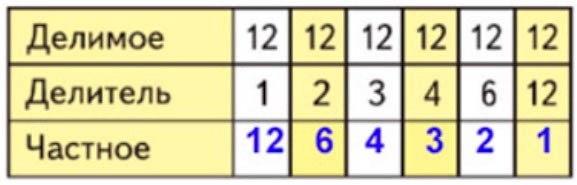
Делаем вывод.
Делимое не изменяется, а делитель увеличивается. Значит, значение частного уменьшается.
Номер 4.
Сравни задачи, сравни их решения.
1) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько стоят 5 таких наборов?
2) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько таких наборов бумаги можно купить на 60 р.?
Задача 1:

1-й способ решения: 1) 80 : 8 = 10 (руб.) – стоит один набор. 2) 10 ∙ 5 = 50 (руб.) Ответ: 50 рублей стоит 5 наборов.
2-й способ решения: 80 : 8 ∙ 5 = 10 ∙ 5 = 50 (р.) – стоят 5 наборов.
Задача 2:

1-й способ решения: 1) 80 : 8 = 10 (руб.) – стоит один набор. 2) 60 : 10 = 6 (н.) Ответ: 6 наборов можно купить на 60 рублей.
2-й способ решения: 60 : (80 : 8 ) = 60 : 10 = 6 (н.) – можно купить наборов на 60 р.
Похожи задачи сюжетом. В обеих неизвестно, сколько стоит 1 набор бумаги. Разница в том, что в первой задаче нужно узнать, сколько стоят 5 наборов (стоимость). А во второй задаче – сколько наборов можно купить (количество).
Данные задачи: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
цена · количество = стоимость.
стоимость : цена = количество.
стоимость : количество = цена.
Оформляем условие в виде таблицы.
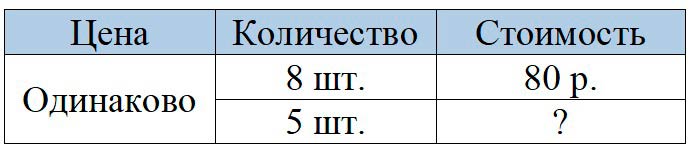
Рассуждаем.
8 одинаковых наборов цветной бумаги стоят 80 рублей. Значит, известно количество наборов и общая стоимость бумаги, но неизвестно цена одного набора цветной бумаге. По таблице видно, что чтобы узнать, сколько стоит один набор бумаги, нужно общую стоимость наборов разделить на количество наборов.
80 : 8 = 10 (руб.) – стоит один набор.
Продолжаем рассуждение.
Мы знаем, что один набор бумаги стоит 10 рублей, а 5 таких наборов – неизвестно рублей. Нам известна цена бумаги, количество наборов, но неизвестна общая стоимость всех наборов. По таблице видно, что общая стоимость 5 наборов складывается из стоимостей каждого набора. Поэтому, вычисляется сложением.
Но цена набора одинаковая. Поэтому сложение одинаковых слагаемых можно заменить умножением.
10 ∙ 5 = 50 (р.) – стоят 5 наборов.
Записываем ответ.
Ответ: 50 рублей стоит 5 наборов.
Решение выражением: 80 : 8 · 5 = 50 (р.),
где 80 : 8 – цена пачки бумаги.
Оформляем условие в виде таблицы.

Рассуждаем.
8 одинаковых наборов цветной бумаги стоят 80 рублей. Значит, известно количество наборов и общая стоимость бумаги, но неизвестно цена одного набора цветной бумаге. По таблице видно, что чтобы узнать, сколько стоит один набор бумаги, нужно общую стоимость наборов разделить на количество наборов.
80 : 8 = 10 (руб.) – стоит один набор.
Продолжаем рассуждение.
Мы знаем, что цена набора – 10 рублей и известная общая стоимость бумаги – 60 рублей. Но неизвестно, сколько наборов можно купить за эти деньги. Значит, известна цена набора и общая стоимость, а количество наборов – неизвестно. Из таблицы видно, что чтобы узнать, количество наборов, нужно общую стоимость наборов разделить на цену набора.
60 : 10 = 6 (н.) – можно купить на 60 р.
Записываем ответ.
Ответ: 6 наборов можно купить на 60 рублей.
Решение выражением: 60 : (80 : 8) = 6 (н.),
где 80 : 8 – цена 1 набора бумаги.
Сходство задач.
Задачи одинаковы тем, что нам известна общая стоимость определенного количества наборов. Также одинаковы первое действие, при котором мы находим сколько стоит цена за 1 набор.
Различие задач.
Различны задачи в том, что нам нужно найти. В первой задаче - стоимость 5 наборов, а во второй задаче – количество наборов на 60 рублей. Поэтому и вторые действия будут разные.
Номер 5.
Ответ:
Перебирай все возможные арифметические действия, производи с ними действия, чтобы понять, каково верное решение.
Рассуждаем.
Расставим знаки действия, чтобы выражения стали верными.
26 – 6 – 7 = 20 – 7 = 13В выражении присутствуют действия вычитания. Выполним их по порядку слева направо.
7 + 9 + 2 = 16 + 2 = 18
В выражении присутствуют действия сложения. Выполним их по порядку слева направо.
9 + 9 + 2 = 18 + 2 = 20
В выражении присутствуют действия сложения. Выполним их по порядку слева направо.
9 · 2 – 2 = 18 – 2 = 16
В данном выражении присутствуют действия вычитание и умножение. Выполним вначале умножение, а потом вычитание.
2 · 2 – 4 = 4 – 4 = 0
В данном выражении присутствуют действия вычитание и умножение. Выполним вначале умножение, а потом вычитание.
8 · 9 – 2 = 72 – 2 = 70
В данном выражении присутствуют действия вычитание и умножение. Выполним вначале умножение, а потом вычитание.
8 · 4 – 2 = 32 – 2 = 30
В данном выражении присутствуют действия вычитание и умножение. Выполним вначале умножение, а потом вычитание.
40 : 5 · 7 = 8 · 7 = 56
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполним действия по порядку слева направо.
Оформляем задание в тетрадь
26 − 6 − 7 = 13
7 + 9 + 2 = 18
9 + 9 + 2 = 20
9 ∙ 2 − 2 = 16
2 ∙ 2 − 4 = 0
8 ∙ 9 − 2 = 70
8 ∙ 4 − 2 = 30
40 : 5 ∙ 7 = 56
Номер 6.
Сравни уравнения каждой пары и скажи, не вычисляя, в каком из них значение х будет больше.
Ответ:
х + 34 = 68
х + 38 = 68
В первом уравнении значение x будет больше, так как второе слагаемое меньше, а значение суммы одинаковое.
96 − х = 15
96 − x = 18
В первом уравнении значение x будет больше, так как уменьшаемое одинаковое, а значение разности меньше.
х − 29 = 60
х − 39 = 60
Во втором уравнении значение x будет больше, так как вычитаемое больше, а значение разности одинаковое.
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения.
Рассмотрим уравнения.
х + 34 = 68 и х + 38 = 68
Значение суммы у двух уравнений одинаковое. Значение суммы скдладывается из суммы первого и второго слагаемых. Во атором уравнении второе слагаемое больше.
96 – х = 15 и 96 – х = 18
Уменьшаемое в уравнениях одинаковое, а значение разности разное. В первом уравнении оно меньше, чем во втором уравнении.
х – 29 = 60 и х = 39 = 60
Значение разности в двух уравнениях одинаково. Вычитаемое в первом уравнении меньше, чем во втором уравнении.
Сравним неизвестные.
x + 34 = 68
x + 38 = 68
В первом уравнении неизвестное х больше, так как при одинаковой сумме второе слагаемое меньше.
96 − x = 15
96 − x = 18
В первом уравнении неизвестное х больше, так как при одинаковом вычитаемом разность меньше.
x − 29 = 60
x − 39 = 60
В первом уравнении неизвестное х меньше, так как при одинаковой разности вычитаемое меньше.
Делаем проверку.
х + 34 = 68
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
х = 68 – 34
х = 34
х + 38 = 68
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
х = 68 – 38
х = 30
34 > 30
Значение неизвестного в первом уравнении больше, чем во втором уравнении.
96 – х = 15
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
х = 96 – 15
х = 81
96 – х = 18
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
х = 96 – 18
х = 78
81 > 78
Значение неизвестного в первом уравнении больше, чем во втором уравнении.
х – 29 = 60
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое.
х = 60 + 29
х = 89
х – 39 = 60
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое.
х = 60 + 39
х = 99
89 < 99
Значение неизвестного во втором уравнении больше, чем в первом уравнении.
Задание внизу страницы
Ответ:24 : 8 = 3 56 : 7 = 8 6 ∙ 8 = 48 8 ∙ 4 = 32
Вспомни названия компонентов действий деления и умножения, а также – зависимости между компонентами и результатом действий деления, умножения.
Рассуждаем.
24 : 8 и 56 : 7 – Нужно найти значение частного.
Чтобы найти неизвестное значение частного, нужно делимое разделитель на делитель.
6 · 8 и 8 · 4 – Нужно найти значение произведения.
Чтобы найти неизвестное значение произведения, нужно первый множитель умножить на второй множитель.
Оформляем задание в тетрадь.
24 : 8 = 6
56 : 7 = 8
6 ∙ 8 = 48
8 ∙ 4 = 32
Задание на полях страницы
Цепочка:

19 + 17 = 36 36 − 12 = 24 24 : 4 = 6 6 ∙ 5 = 30
Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Выполним устные рассуждения.
19 + 17 = 19 + (11 + 6) = (19 + 11) + 6 = 30 + 6 = 36
Представим число 17 в виде суммы чисел 11 и 6. Вначале к числу 19 прибавим число 11, а потом прибавим число 6.
36 – 12 = (32 + 4) – 12 = (32 – 12) + 4 = 20 + 4 = 24
Разложим число 36 на сумму чисел 32 и 4. Вначале из числа 32 вычтем число 12, а потом к полученной разности прибавим число 4.
24 : 4 = 6,
так как 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 5 = 30,
где 6 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
19 + 17 = 36
36 − 12 = 24
24 : 4 = 6
6 ∙ 5 = 30
19 + 17 = 36 → 36 − 12 = 24 → 24 : 4 = 6 → 6 · 5 = 30
Площадь квадрата, сторона которого 1 дм, — это единица площади — квадратный дециметр. Слова «квадратный дециметр» при числах записывают так: 5 дм2, 17 дм2.
Номер 1.
На чертеже изображён 1 дм2, который разбит на квадратные сантиметры.
- Объясни, как подсчитать, сколько квадратных сантиметров содержится в квадратном дециметре.


Сторона квадрата равна 10 см, а площадь квадрата равна произведению его сторон: 10 · 10 = 100 см2 Тогда, 1 дм2 = 100 см2
1) 1 дм2 – это еще одна единица измерения площади.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Рассмотрим 1 способ решения.
Рассмотрим квадрат 1 дм2, который разбит на квадратные сантиметры.
Стороны квадрата равны, в них укладывается 10 квадратов со стороной 1 см, значит, сторона большого квадрата – 10 см, т.е. 1 дм, потому что 10 см = 1 дм.
Выходит, что площадь большого квадрата со стороной 10 см равна 100 дм2, потому что:
а · а = 10 см · 10 см = 100 см2.
И 100 см2 = 1 дм2, ведь стороны 10 см = 1 дм.
Рассмотрим 2 способ решения.
Мы знаем, что площадь квадрата равна 1 дм2 и он разбит на квадраты со стороной 1 см. Значит площадь маленького квадрата равна:
1 см · 1 см = 1 см2
Чтобы узнать площадь квадрата в см2 можно посчитать количество квадратов из которых он состоит.
Их количество – 100.
Значит, площадь квадрата равна 100 см2
Значит, 1 дм2 = 100 см2
Записываем ответ.
Ответ: 1 дм2 = 100 см2.
Номер 2.
На обороте обложки учебника изображён квадрат площадью 1 дм2. Красными линиями выделены два прямоугольника. Найди площадь каждого из них.
Ответ:1) 5 ∙ 5 = 25 см2 2) 6 ∙ 8 = 48 см2 Ответ: площадь первого прямоугольника 25 см2, площадь второго прямоугольника 48 см2.
Площадь фигуры измеряется в квадратных единицах.
Рассмотрим первый прямоугольник.
Квадрат со сторой 1 дм2 разбит на 100 квадратов со стороной 1 см, так как 10 см = 1 дм.
-(2023).jpg)
Первый прямоугольник состоит из 5 квадратов в 1 см в длину и из 5 квадратов в 1 см в ширину. Значит это фигура квадрат со стороной 5 см.
Чтобы вычислить площадь, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Длина и ширина у квадрата одинакова и равна 5 см.
5 см · 5 см = 25 cм2 – площадь квадрата со сторной 5 см.
Проверить это можно если сосчитаем количесвто клеток – их 25.
Рассмотрим второй пярмоугольник.
-(2023).jpg)
Первый прямоугольник состоит из 8 квадратов в 1 см в длину и из 6 квадратов в 1 см в ширину. Значит это прмяоугльник со сторонами 8 см и 6 см.
Чтобы вычислить площадь, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
У прямоугольника длина равна 8 см, а ширина равна 6 см.
8 см · 6 см = 48 cм2 – площадь прямоугольника со сторнами 8 см и 6 см.
Проверить это можно если сосчитаем количесвто клеток – их 48.
Оформляем задание в тетрадь.
Первый прямоугольник состоит из 5 квадратов в 1 см в длину и из 5 квадратов в 1 см в ширину. Это фигура квадрат.
5 ∙ 5 = 25 (cм2) − площадь первого прямоугольника (квадрата).
Второй прямоугольник состоит из 8 квадратов в 1 см в длину и из 6 квадратов в 1 см в ширину.
6 ∙ 8 = 48 (cм2) − площадь второго прямоугольника.
Ответ: площадь первого прямоугольника – 25 cм2 второго – 48 cм2.
Номер 3.
Высота зеркала прямоугольной формы 10 дм, а ширина 5 дм. Чему равна площадь зеркала?
Ответ:а = 10 дм b = 5 дм S = ? дм2 S = a ∙ b S = 10 ∙ 5 S = 50 дм2 Ответ: Площадь зеркала составляет 50 дм2.
1) Площадь фигуры измеряется в квадратных единицах.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Оформляем условие в виде краткой записи.
.jpg)
Длина – 10 дм
Ширина – 5 дм
Площадь – ?
Рассуждаем.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Дина равна 10 дм, а ширина равна 5 дм.
10 дм · 5 дм = (5 · 10) дм2 = 50 дм2 – площадь зеркала.
Записываем ответ.
Ответ: площадь зеркала 50 дм2.
Задание на полях страницы.


Проверка:
Первая рамка:
14 + 15 + 7 = 14 + 22 = 36
7 + 11 + 18 = 18 + 18 = 36
14 + 4 + 18 = 18 + 18 = 36
Вторая рамка:
18 + 44 + 10 = 28 + 44 = 72
10 + 12 + 50 = 22 + 50 = 72
18 + 4 + 50 = 22 + 50 = 72
Занимательные рамки – рамки, в которых числа, стоящие на одной прямой, образуют в сумме число, записанное в центре рамки.
Рассуждаем.
Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – это число 36.
Находим неизвестные числа.
14 + 15 + 7 = 29 + 7 = 36
14 + 4 + 18 = 18 + 18 = 36
7 + 11 + 18 = 36
Заполняем рамку числами.
-(2023).jpg)
Рассуждаем.
Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – этот число 72.
18 + 44 + 10 = 62 + 10 = 72
18 + 4 + 50 = 68 + 4 = 72
10 + 12 + 50 = 60 + 12 = 72
Заполняем рамку числами.
-(2023).jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.