Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 62

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Вычисли и запомни!

8 ∙ 8 = 64 64 : 8 = 8 8 ∙ 9 = 72 9 ∙ 8 = 72 72 : 8 = 9 72 : 9 = 8
Номер 1.
Ответ:
9 ∙ 8 = 72 64 : 8 = 8
8 ∙ 8 = 64 56 : 8 = 7
7 ∙ 7 = 49 72 : 8 = 9
5 ∙ 2 = 10 36 : 4 = 9
3 ∙ 9 = 27 27 : 3 = 9
2 ∙ 6 = 12 18 : 2 = 9

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления.
Выполним умножение.
9 · 8 = 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним деление.
64 : 8 = 8,
так как 8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
56 : 8 = 7,
так как 8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
72 : 8 = 9,
так как 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
Расставляем порядок действий и выполняем вычисления.
2 1
96 − 56 : 8 = 89
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем деление, а потом вычитание.
1) 56 : 8 = 7, так как 7 · 8 = 56
2) 96 − 7 = 96 – (6 + 1) = (96 – 6) – 1 = 90 – 1 = 89
Число 7 представим в виде суммы чисел 6 и 1. Вначале из числа 96 вычтем число 6, а потом вычтем число 1.
1 2
21 : 3 + 18 = 25
В данном выражении присутствуют действия сложение и деление. Вначале выполняем деление, а потом сложение.
1) 21 : 3 = 7, так как 3 · 7 = 21
2) 7 + 18 = (5 + 2) + 18 = 5 + (2 + 18) = 5 + 20 = 25
Число 7 представим в виде суммы чисел 5 и 2. Вначале к числу 18 прибавим число 2, а потом прибавим число 5.
2 1
40 − 15 : 5 = 37
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем деление, а потом вычитание.
1) 15 : 5 = 3, так как 3 · 5 = 15
1) 40 − 3 = (30 + 10) – 3 = 30 + (10 – 3) = 30 + 7 = 37
Число 40 представим в виде суммы чисел 30 и 10. Вначале из числа 10 вычтем число 3, а потом к числу 30 прибавим полученную разность.
Выполним умножение.
5 · 2 = 10,
где 5 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
2 · 6 = 12,
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Выполним деление.
36 : 4 = 9,
так как 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
26 : 3 = 9,
так как 3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
18 : 2 = 9,
так как 2 · 9 = 18,
где 2 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
9 ∙ 8 = 72
8 ∙ 8 = 64
7 ∙ 7 = 49
64 : 8 = 8
56 : 8 = 7
72 : 8 = 9
96 – 56 : 8 = 96 – 7 = 89
21 : 3 + 18 = 7 + 18 = 25
40 – 15 : 5 = 40 – 3 = 37
5 ∙ 2 = 10
3 ∙ 9 = 27
2 ∙ 6 = 12
36 : 4 = 9
27 : 3 = 9
18 : 2 = 9
Номер 2.
Ответ:
с · 8, значит, умножить число на 8, то есть увеличить в 8 раз.
Промежуточные вычисления.
с · 8, если:
с = 1, то 1 · 8 = 8,
Если любое число умножить на 1, то число не изменится.
с = 2, то 2 · 8 = 16,
где 2 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 3, то 3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 4, то 4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 5, то 5 · 8 = 40,
где 5 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 6, то 6 · 8 = 48, где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 7, то 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 8, то 8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
с = 9, то 9 · 8 = 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
Заполним таблицу.
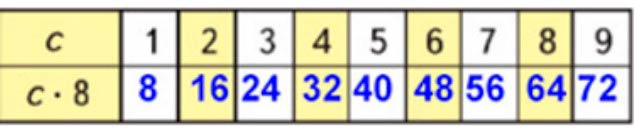
Номер 3.
В зоомагазине в 6 аквариумах 54 рыбки, поровну в каждом. Сколько аквариумов занимают 27 рыбок?
Ответ:
1-й способ решения: 1) 54 : 6 = 9 (р.) – в одном аквариуме. 2) 27 : 9 = 3 (акв.) Ответ: 3 аквариума потребуется для 27 рыбок.
2-й способ решения: 27 : (54 : 6) = 27 : 9 = 3 (акв.) - потребуется для 27 рыбок. Ответ: 3 аквариума.
Данная задача: вида «кол-во рыб в 1 аквариуме, кол-во аквариумов, общее кол-во рыб» характеризуется зависимостями между компонентами:
Кол-во рыб в 1 аквариуме · кол-во аквариумов = общее кол-во рыб.
Общее кол-во рыб : кол-во аквариумов = кол-во рыб в 1 аквариуме.
Общее кол-во рыб : кол-во рыб в 1 аквариуме = кол-во аквариумов.
Оформляем условие в виде таблицы.
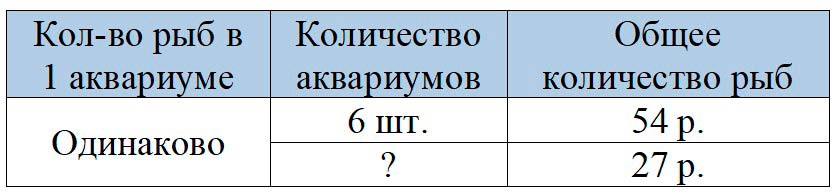
Рассуждаем.
В 6 аквариумах 54 рыбки. Значит, известно количество аквариумов и общее количество рыбы, но неизвестно количество рыб в 1 аквариуме. Из таблицы видно, что количество рыб в 1 аквариуме одинаковое, значит, чтобы узнать, сколько рыбы было в 1 аквариуме, нужно общее количество рыбы разделить на количество аквариумов.
54 : 6 = 9 (р.) – в одном аквариуме.
Продолжаем рассуждение.
Мы узнали, что в 1 аквариуме – 9 рыбок, а всего рыбок – 27. Неизвестно, сколько аквариумов потребовалось. Значит, чтобы узнать, сколько аквариумов нужно, нужно общее количество рыб разделить на количество рыб в 1 аквариуме.
27 : 9 = 3 (акв.) - потребуется для 27 рыбок.
Записываем ответ.
Ответ: 3 аквариума потребуется для 27 рыбок.
Решение выражением: 27 : (54 : 6) = 3 (акв.),
где 54 : 6 – количество рыб в 1 аквариуме.
Номер 4.
1) В огороде собрали 24 кг лука, чеснока в 4 раза меньше, чем лука, а моркови в 5 раз больше, чем чеснока. Сколько килограммов моркови собрали?
2) Составь задачу по выражению (15 : 3) ∙ 2.
Задача 1:

1-й способ решения: 1) 24 : 4 = 6 (кг) – собрали чеснока. 2) 6 ∙ 5 = 30 (кг) Ответ: всего собрали 30 кг моркови.
2-й способ решения: 24 : 4 ∙ 5 = 6 ∙ 5 = 30 (кг) - собрали моркови. Ответ: 30 кг.
Задача 2: Карандаш стоит 15 р., а ластик в 3 раза дешевле карандаша, ручка в 2 раза дороже ластика. Сколько стоит ручка?
Задача 1:
1) «в 4 раза меньше», значит, вычисляется делением.
2) «в 5 раз больше», значит, вычисляется умножением.
Задача 2:
Карандаш стоит 15 р., а ластик в 3 раза дешевле карандаша, ручка в 2 раза дороже ластика. Сколько стоит ручка?
Оформляем условие в виде краткой записи.
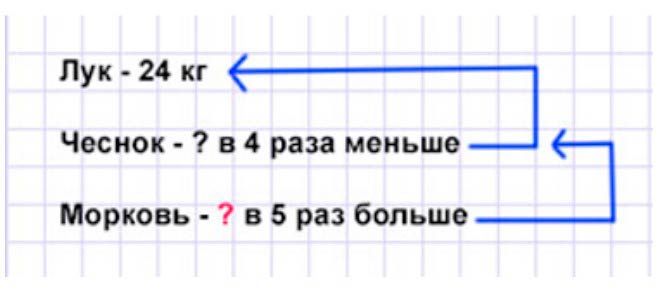
Рассуждаем.
В огороде собрали 24 кг лука, а чеснока в 4 раза меньше. Значит, чтобы узнать, сколько чеснока собрали, нужно общее количество лука разделить на 4.
24 : 4 = 6 (кг) – собрали чеснока.
Продолжаем рассуждение.
Мы узнали, что в огороде собрали 6 кг чеснока. А моркови собрали в 5 раз больше, чем чеснока. Значит, чтобы узнать, сколько моркови собрали, нужно количество чеснока умножить на 5.
6 ∙ 5 = 30 (кг) - собрали моркови.
Записываем ответ.
Ответ: 30 кг собрали моркови.
Решение выражением: (24 : 4) · 5 = 30 (кг),
где 24 : 4 – количество чеснока который собрали.
Оформляем условие в виде краткой записи.

Рассуждаем.
Карандаш стоит 15 рублей, а ластик – в 3 раза дешевле карандаша. Значит, чтобы узнать, сколько стоит ластик, нужно стоимость карандаша разделить на 3.
15 : 3 = 5 (руб.) – стоит ластик.
Продолжаем рассуждение.
Ластик стоит 5 рублей, а ручка – в 2 раза дороже. Чтобы узнать, сколько стоит ручка, нужно стоимость ластика умножить на 2.
5 · 2 = 10 (руб.) – стоит ручка.
Записываем ответ.
Ответ: 10 рублей стоит ручка.
Решение выражением: (15 : 3) · 2 = 10 (руб.),
где 15 : 3 – стоимость ластика.
Номер 5.
Начерти прямоугольник ABCD, длины сторон которого 8 см и 2 см. Найди его площадь и периметр.
Ответ:
Р = 8 + 8 + 2 + 2 = 20 (см) S = 2 ∙ 8 = 16 (см2) Ответ: периметр прямоугольника составляет 20 см, а площадь прямоугольника - S 16 см2
1) Площадь фигуры измеряется в квадратных сантиметрах (см2).
2) Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Начертим прямоугольник.
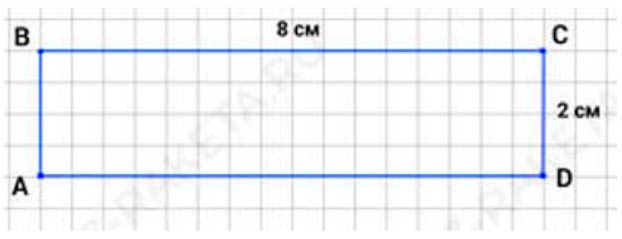
Длина – 8 см
Ширина – 2 см
Периметр – ?
Площадь – ?
Рассуждаем.
У прямоугольника длина равна – 8 см, а ширина – 2 см. Значит для того чтобы вычислить площадь прямоугольника умножим длину на ширину.
8 · 2 = 16 (см2) – площадь прямоугольника.
Продолжаем рассуждение.
Периметр – это сумма длин всех сторон.
Периметр прямоугольника можно вычислить несколькими способами:
Способ 1: сложить все стороны.
8 + 8 + 2 + 2 = (8 + 2) + (8 + 2) = 10 + 10 = 20 (см).
Споосб 2: поотдельности длину и ширину умножить на 2, а потом полученные произвдения сложить.
8 · 2 + 2 · 2 = 16 + 4 = 20 (см).
Споосб 3: сложить длину и ширину и полученную сумму умножить на 2.
(8 + 2) · 2 = 10 · 2 = 20 (см).
Записываем ответ.
Ответ: площадь – 18 см2; периметр 20 см.
Номер 6.
Реши уравнения, в которых неизвестное находят вычитанием.
Ответ:
Уравнение х - 27 = 54 не подходит, т.к. неизвестное находится сложением.
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения.
Рассмотрим уравнения.
Проанализируем все уравнения, посмотрим, чем является неизвестное, т.е. каким компонентом, чтобы понять, как найти неизвестный компонент, зная два других.
х – 27 = 54,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое. Неизвестное находится сложением.
100 – х = 63,
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности. Неизвестное находится вычитанием.
х + 18 = 67,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое. Неизвестное находится вычитанием.
Решим уравнения.
Решим уравнения, в которых неизвестное находят вычитанием. Это второе и третье уравнения.
100 − x = 63
x = 100 − 63
x = 37
x + 18 = 67
x = 67 − 18
x = 49
Делаем проверку.
100 – х = 63
Проверка: вместо неизвестного подставим число 37.
100 – 37 = (90 + 10) – 37 = (90 – 30) + (10 – 7) = 60 + 3 = 63
63 = 63 – верно.
х + 18 = 67
Проверка: вместо неизвестного подставим число 49.
49 + 18 = 49 + (1 + 17) = (49 + 1) + 17 = 50 + 17 = 67
67 = 67 – верно.
Оформляем задание в тетрадь.
х – 27 = 54
х – уменьшаемое, находится сложением вычитаемого и разности.
100 − x = 63
x = 100 − 63
x = 37
x + 18 = 67
x = 67 − 18
x = 49
Номер 7.
Одинаковые фигуры обозначают одинаковые числа. Какое число прячется под треугольником? под квадратом? под кругом?

Под треугольником прячется число 2. Под квадратом прячется число 4. Под кругом прячется число 3. Проверка: 12 = 3 · 2 · 2 12 = 3 · 4 24 = 2 · 2 · 2 · 3 24 = 2 · 3 · 6
1) Рассуждение начни со второго выражения.
2) Вспомни, каковы компоненты действия умножения и какими они могут быть при значении произведения 12.
Рассмотрим 1 и 2 выражение.
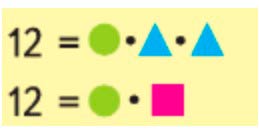
Из первых двух выражений видно, что 1 квадрат равен произведению 2 треугольникам и данное произведение не превышает 12.
= ▲ · ▲
Подходит только один вариант, где произведение не превышало число 12:
4 = 2 ∙ 2
Значит, 4 – квадрат, а 2 – треугольник.
Рассмотрим 4 выражение.

Вместо квадрата подставим число 4, а вместо треугольника число 2.
Получим выражение:
24 = 2 · ◯ · 4
Упростим выражение умножив 2 на 4.
24 = 8 · ◯
Круг – это неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
◯ = 24 : 8
◯ = 3
Делаем проверку.
Во все выражения подставим вместо треугольник число 2, вместо квадрата число 4, вместо круга число 3.
12 = 3 ∙ 2 ∙ 2
3 · 2 · 2 = 6 · 2 = 12
12 = 12 - верно.
12 = 3 ∙ 4
3 · 4 = 12
12 = 12 – верно.
24 = 2 ∙ 2 ∙ 2 ∙ 3
2 · 2 · 2 · 3 = 4 · 6 = 24
24 = 24 – верно.
24 = 2 ∙ 3 ∙ 4
2 · 3 · 4 = 6 · 4 = 24
24 = 24 – верно.
Записываем ответ.
Ответ: треугольник – 2, квадрат – 4, круг – 3.
Задание внизу страницы
Ответ:8 ∙ 9 = 72 28 : 7 = 4 16 + 20 : 4 = 16 + 5 = 21 3 ∙ 8 = 24 32 : 8 = 4
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
40 Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий и выполняем вычисления.
8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
28 : 7 = 4,
так как 7 · 4 = 28,
где 7 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
В данном выражении присутствуют действия сложение и умножение. Вначале выполняем умножение, а потом сложение.
1) 20 : 4 = 5, так как 4 · 5 = 20
2) 16 + 5 = 16 + (4 + 1) = (16 + 4) = 1 = 20 + 1 = 21
Представим число 5 в виде суммы чисел 4 и 1. Вначале к числу 16 прибавим число 4, а потом прибавим число 1.
3 · 8 = 24,
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
32 : 8 = 4,
так как 8 · 4 = 32,
где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
8 ∙ 9 = 72
28 : 7 = 4
16 + 20 : 4 = 16 + 5 = 21
3 ∙ 8 = 24
32 : 8 = 4
Номер 1.
42 : 6 + 91 : 9 27 : 9 + 41 7 · 6 – 9 · 4 72 : 9 + 72 : 8 61 – 48 : 8 9 · 6 – 45 : 9 36 : 4 – 18 : 2 36 + 8 · 8 8 · 4 + 56 :7
Ответ:
42 : 6 + 81 : 9 = 7 + 9 = 16
72 : 9 + 72 : 8 = 8 + 9 = 17
36 : 4 – 18 : 2 = 9 – 9 = 0
27 : 9 + 41 = 3 + 41 = 44
61 – 48 : 8 = 61 – 6 = 55
36 + 8 · 8 = 36 + 64 = 100
7 · 6 – 9 · 4 = 42 – 36 = 6
9 · 6 – 45 : 9 = 54 – 5 = 49
8 · 4 + 56 : 7 = 32 + 8 = 40
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
40 Для выполнения задания обращайся к таблице умножения и деления.
Выполняем вычисления.
42 : 6 + 81 : 9 = 16
1) 42 : 6 = 7
2) 81 : 9 = 9
3) 7 + 9 = 16
72 : 9 + 72 : 8 = 17
1) 72 : 9 = 8
2) 72 : 8 = 9
3) 8 + 9 = 17
36 : 4 – 18 : 2 = 0
1) 36 : 4 = 9
2) 18 : 2 = 9
3) 9 – 9 = 0
27 : 9 + 41 = 44
1) 27 : 9 = 3
2) 3 + 41 = 44
61 – 48 : 8 = 55
1) 48 : 8 = 6
2) 61 – 6 = 55
36 + 8 · 8 = 100
1) 8 · 8 = 64
2) 36 + 64 = 100
7 · 6 – 9 · 4 = 6
1) 7 · 6 = 42
2) 9 · 4 = 36
3) 42 – 36 = 6
9 · 6 – 45 : 9 = 49
1) 9 · 6 = 54
2) 45 : 9 = 5
3) 54 – 5 = 49
8 · 4 + 56 : 7 = 40
1) 8 · 4 = 32
2) 56 : 7 = 8
3) 32 + 8 = 40
Оформляем задание в тетрадь.
42 : 6 + 81 : 9 = 7 + 9 = 16
72 : 9 + 72 : 8 = 8 + 9 = 17
36 : 4 – 18 : 2 = 9 – 9 = 0
27 : 9 + 41 = 3 + 41 = 44
61 – 48 : 8 = 61 – 6 = 55
36 + 8 · 8 = 36 + 64 = 100
7 · 6 – 9 · 4 = 42 – 36 = 6
9 · 6 – 45 : 9 = 54 – 5 = 49
8 · 4 + 56 : 7 = 32 + 8 = 40
Номер 2.


Чтобы найти делимое, нужно делитель умножить на частное.
Чтобы найти делитель, нужно делимое разделить на частное.
Выполняем вычисления.
3 · 8 = 24
24 : 4 = 6
3 : 3 = 1
49 : 7 = 7
6 · 7 = 42
72 : 9 = 8
56 : 8 = 7
Заполняем таблицу.
.jpg)
Номер 3.
В 9 коробок разложили поровну 72 машинки. Сколько машинок в 7 таких коробках?
Ответ:9 к. — 72 м 7 к. — ? м. 1) 72 : 9 = 8 (м) — в одной коробке 2) 8 · 7 = 56 (м). Ответ: 56 машинок всего в 7 таких коробках
Краткая запись — это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие задачи в виде краткой записи.
9 к. — 72 м
7 к. — ? м.
Рассуждаем.
Вычислим, сколько машинок в одной коробке, для этого количество машинок в девяти коробках разделим на количество коробок.
1) 72 : 9 = 8 (м) — в одной коробке
Продолжаем рассуждение.
Теперь мы можем узнать, сколько машинок в семи коробках, для этого количество машинок в одной коробке умножим на 7.
2) 8 · 7 = 56 (м)
Записываем ответ.
Ответ: 56 машинок в семи коробках.
Номер 4.
В книге 90 страниц. В первый день Оля прочитала 15 страниц, а во второй день — на 5 страниц больше. Сколько страниц этой книги Оле осталось прочитать?
Ответ:
1) 15 + 5 = 20 (стр.) - прочитала Оля во второй день.
2) 90 - 20 = 70 (стр.) - книги осталось прочитать.
Ответ: 70 страниц осталось прочитать Оли от всей книги.
Краткая запись — это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие задачи в виде краткой записи.
Всего – 90 стр.
1 день – 15 стр.
2 день – ?, на 5 стр. >, чем в 1-й день.
Осталось – ?
Рассуждаем.
Чтобы узнать, сколько страниц Оля прочитала во второй день, нужно к количеству страниц, прочитанных в первый день прибавить 5, потому что известно, что во второй день Оля прочитала на пять страниц больше, чем в первый.
1) 15 + 5 = 20 (стр.) – прочитала во второй день
Продолжаем рассуждение.
Узнаем, сколько страниц Оля прочитала за первый и второй дни вместе.
2) 15 + 20 = 35 (стр.) – прочитала за два дня
Продолжаем рассуждение.
Чтобы узнать, сколько страниц осталось прочитать, нужно из общего количества страниц вычесть количество страниц, которое Оля уже прочитала.
3) 90 – 35 = 55 (стр.)
Записываем ответ.
Ответ: 55 страниц осталось прочитать.
Номер 5.
На столе лежали карандаши. После того как половину всех карандашей Таисия убрала в пенал, на столе осталось 5 карандашей. Сколько карандашей было на столе?
Ответ:
Было - ? шт.
Убрали - ? шт., половина
Осталось - ? шт.
5 · 2 = 10 (шт.) - карандашей было на столе
Ответ: 10 карандашей было на столе всего.
Повторим таблицу умножения.
Рассуждаем.
Известно, что убрала Таисия половину, а осталось 5, значит 5 - это вторая половина.
5 · 2 = 10 (к.)
Записываем ответ.
Ответ: 10 карандашей было.
Номер 6.
В первый день каникул Дима катался на лыжах 30 минут, во второй день — в 2 раза дольше, а в третий день столько, сколько в два первых дня вместе. Сколько минут Дима катался на лыжах в третий день?
Ответ:
1) 30 · 2 = 60 (мин) - катался на лыжах Дима в первый день
2) 30 + 60 = 90 (мин) - Дима катался на лыжах в третий день.
Ответ: 90 минут катался на лыжах Дима в третий день.
Краткая запись — это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие задачи в виде краткой записи.
.jpg)
Рассуждаем.
Узнаем, сколько минут катался Дима во второй день, для этого время катания в первый день умножаем на 2, потому что известно, что во второй день он катался в 2 раза дольше.
1) 30 · 2 = 60 (мин) − катался во второй день
Продолжаем рассуждение.
Чтобы узнать, сколько минут катался Дима в третий день, нужно сложить вместе количество времени, которое Дима катался в первый и второй день.
2) 30 + 60 = 90 (мин)
Записываем ответ.
Ответ: 90 минут катался Дима в третий день.
Номер 7.
Построй линейную диаграмму, используя решение задачи 6. Покажи на диаграмме, сколько минут Дима катался на лыжах в каждый день каникул.
Ответ:
Столбчатая диаграмма - это схема в виде прямоугольной области, на которой столбиками показаны данные. Значение каждой числовой группы показывается высотой столбика и соответствует шкале.
В линейной диаграмме столбики заменяют линии. С помощью такой диаграммы удобно сравнивать показатели и выполнять различные действия с полученными значениями.
Вспомним данные задачи №6.
1 день – 30 мин.
2 день – 60 мин.
3 день – 90 мин.
Построим диаграмму.
.jpg)
Номер 8.
Начерти ломаную из трёх звеньев, длина которой 14 см. При этом длина одного звена 3 см, а другое — в 2 раза длиннее.
Ответ:1 з. – 3 см 2 3. В 2 > см 3 з. – ? см Всего 14 см 1) 3 · 2 = 6 (см) — второе звено 2) 14 – 3 – 6 = 5 (см) — третье звено Ответ: :Длины звеньев ломаной: 3 см, 5 см, 6 см

Ломаная – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.
Оформляем условие задачи в виде краткой записи.
1 зв. – 3 см
2 зв. – в 2 > см, чем 1 звено.
3 зв. – ? см
Всего – 14 см
Рассуждаем.
Узнаем, чему равна длина второго звена, для этого длину первого звена умножим на 2, потому что известно, что оно в 2 раза длиннее.
1) 2 · 3 = 6 (см) – второе звено.
Продолжаем рассуждение.
Чтобы узнать, чему равна длина третьего звена, нужно из длины всей ломаной вычесть длину первого и второго звеньев.
2) 14 – 3 – 6 = 5 (см) – третье звено.
Записываем ответ.
Ответ: 3 см, 5 см, 6 см.
Чертим ломаную.
.jpg)
Номер 9.
Как рассадить 45 цыплят в 9 клеток так, чтобы во всех клетках было:
1) равное число цыплят;
2) разное число цыплят.
1) 45 : 9 = 5 (ц) — в каждой клетке 2) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 (ц) — в первой клетке 1 цыпленок, во второй клетке 2 цыпленка, то есть, в каждой последующей клетке на одного цыпленка больше
Деление – разбивание определенного количества предметов на равные части.
Рассадим цыплят, чтоб в каждой клетке было одинаково.
Чтобы во всех клетках было одинаковое количество цыплят, нужно количество цыплят разделить на количество клеток.
1) 45 : 9 = 5 (ц) – в каждой клетке.
Рассадим цыплят, чтоб в каждой клетке было разное количество.
2) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 (ц) — в первой клетке 1 цыпленок, во второй клетке 2 цыпленка, то есть, в каждой последующей клетке на одного цыпленка больше.
Задание внизу страницы.
7 · 9 54 : 9 7 · 8 72 : 8 9 · 9
Ответ:7 · 9 = 63 54 : 9 = 6 7 · 8 = 56 72 : 8 = 9 9 · 9 = 81
Повторим таблицу умножения.
Выполняем вычисления.
7 · 9 = 63
54 : 9 = 6
7 · 8 = 56
72 : 8 = 9
9 · 9 = 81
Оформляем задание в тетрадь.
7 · 9 = 63
54 : 9 = 6
7 · 8 = 56
72 : 8 = 9
9 · 9 = 81
Задание на полях страницы.

9 : 9 = 1 18 : 9 = 2 27 : 9 = 3 36 : 9 = 4 45 : 9 = 5 54 : 9 = 6 Лишнее число 35, оно не делится на 9
Повторим таблицу умножения.
Выполним вычисления, чтобы узнать, какое число лишнее.
9 : 9 = 1
18 : 9 = 2
27 : 9 = 3
36 : 9 = 4
45 : 9 = 5
54 : 9 = 6
Лишнее число 35, оно не делится на 9.
Запишем ответ.
Ответ: 35 – лишнее число.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.