Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 55

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 23.
Сравни задачи. В чем их различия? Реши задачи и объясни, чем различаются их решения.
1) В одной книге 60 страниц, а в другой – 10. Во сколько раз больше страниц в одной книге, чем в другой?
2) В одной книге 60 страниц, а в другой – 10. На сколько больше страниц в одной книге, чем в другой?
Задачи похожи тем, что мы знаем, сколько страниц в первой и во второй книгах. Различаются вопросами. В первой просят узнать, во сколько раз больше страниц в одной книге, чем в другой. Во второй задаче – на сколько больше. Поэтому и решение будут разными: в первой с помощью деления, во второй – с помощью вычитания.
Задача 1:

60 : 10 = 6 (раз)
Ответ: в 6 раз больше страниц в одной книге, чем во второй.
Задача 2:

60 − 10 = 50 (стр.) Ответ: на 50 страниц больше в одной книге, чем во второй.
1) Задача 1: Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) Задача 2: Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
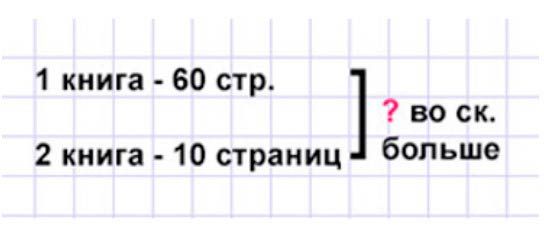
Рассуждаем.
В первой книге 60 страниц, а во второй – 10 страниц. Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Значит, нужно количество книг первой книги разделить на количество книг второй книги.
60 : 10 = 6 (раз) – во сколько больше.
Записываем ответ.
Ответ: в 6 раз больше.
Оформляем условие в виде краткой записи.
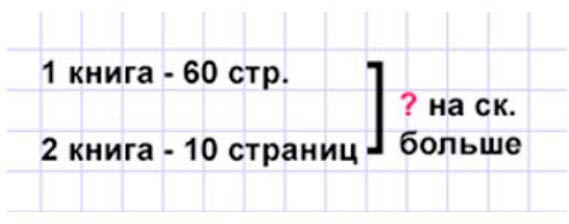
Рассуждаем.
В первой книге 60 страниц, а во второй – 10 страниц. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее, т.е. из количества страниц первой книги вычесть количество страниц второй книги.
60 − 10 = 50 (стр.) – на сколько больше.
Записываем ответ.
Ответ: на 50 страниц больше.
Сравним задачи.
Задачи похожи данными. Различаются вопросами. В первой просят узнать, во сколько раз больше страниц в одной книге, чем в другой - вычисляется делением. Во второй задаче – на сколько больше – вычисляется вычитанием. В итоге решение и ответ будут разные.
Номер 24.
Ответ:
1) а · 6, значит, увеличить число в 6 раз, т.е. умножить на 6.
2) а + 6, значит, прибавить к числу 6, т.е. увеличить на 6 единиц.
Рассмотрим первый столбец.
При а = 8
а · 6 = 8 · 6 = 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество слагаемых.
а + 6 = 8 + 6 = 8 + (2 + 4) = (8 + 2) + 4 = 10 + 4 = 14
Рассмотрим второй столбец.
Получается уравнение:
а + 6 = 10
а – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
а = 10 – 6
а = 4.
При а = 4;
а · 6 = 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Рассмотри третий столбец.
Получается уравнение:
а · 6 = 18
а – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
а = 18 : 6
а = 3
При а = 3
а + 6 = 3 + 6 = 9
Рассмотрим четвёртый столбец.
При а = 7
а · 6 = 7 · 6 = 42,
где 7 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
а + 6 = 7 + 6 = 7 + (3 + 3) = (7 + 3) + 3 = 10 + 3 = 13
Рассмотрим пятый столбик.
Получается уравнение:
а · 6 = 24
а – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
а = 24 : 6
а = 4
При а = 4;
а + 6 = 4 + 6 = 10
Рассмотрим шестой столбик.
При а = 5;
а · 6 = 5 · 6 = 30,
где а – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
а + 6 = 5 + 6 = 5 + (5 + 1) = (5 + 5) + 1 = 10 + 1 = 11
Рассмотрим седьмой столбик.
Получается уравнение:
а + 6 = 15
а – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
а = 15 – 6
а = 9
При а = 9;
а · 6 = 9 · 6 = 6 · 9 = 54
Применяем переместительное свойство умножения,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Подставим числа в таблицу.
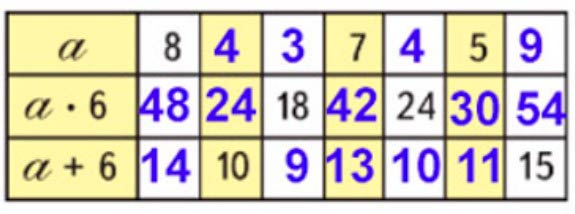
Номер 25.
1) Начерти прямоугольник, длины сторон которого 6 см и 2 см, и найди его периметр.
2) Начерти другой прямоугольник, периметр которого равен периметру начерченного прямоугольника, а длина одной из сторон равна 3 см.

1-й способ решения: Р = 6 ∙ 2 + 2 ∙ 2 = 16 см
2-й способ решения: (6 + 2) ∙ 2 = 8 ∙ 2 = 16 (см) – периметр АВСD
3-й способ решения: 6 ∙ 2 + 2 ∙ 2 = 12 + 4 = 16 (см) – периметр АВСD
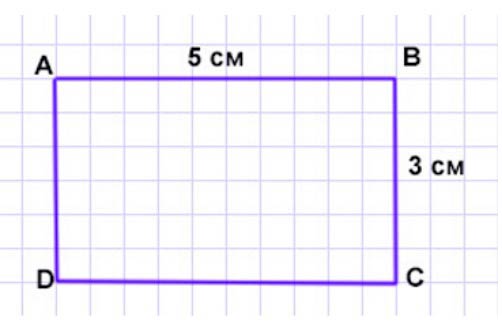
2)
Р = 16 см Если ширина 3 см, то длина: 16 : 2 - 3 = 5 см
Прямоугольник – замкнутая ломаная, четырехугольник, у которого все углы прямые, а стороны попарно равны.
Начертим прямоугольник.
Начертим прямоугольник со сторонами 6 см и 2 см.
Назовём полученный прямоугольник АВСD.
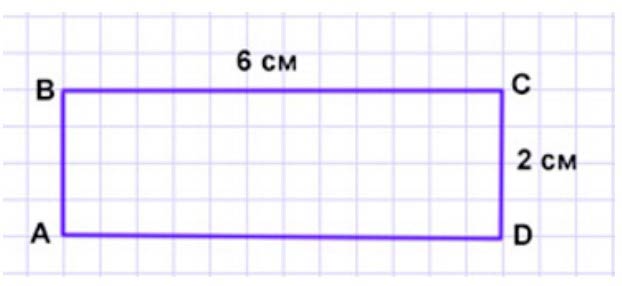
Рассуждаем.
Периметр прямоугольник – сумма длин всех его сторон.
При этом периметр многоугольника можно вычислить несколькими способами:
1 способ: а + в + а + в – сложение всех сторон.
2 способ: а · 2 + в · 2 – каждую сторону умножить на 2 и полученные результаты сложить.
3 способ: (а + в) · 2 – сложить две стороны прямоугольника и результат умножить на 2.
Найдём периметр.
Найдём периметр прямоугольника 3 способами:
Способ 1:
6 см + 2 см + 6 см + 2 см = 8 см + 8 см = 16 см – периметр АВСD
Способ 2:
(6 + 2) ∙ 2 = 8 ∙ 2 = 16 (см) – периметр АВСD
Способ 3:
6 ∙ 2 + 2 ∙ 2 = 12 + 4 = 16 (см) – периметр АВСD
Периметр прямоугольник равен 16 см.
Рассуждаем.
Нужно начертить другой прямоугольник такой, чтобы у него был такой же периметр, то есть 16 см, а стороны были иными.
Периметр прямоугольника равен 16 см. Значит сумма двух сторон равна половине периметра прямоугольника.
16 : 2 = 8 (см) – сумма длин прямоугольника.
Продолжаем рассуждение.
Сумма длин двух сторон равна 8 см, а длина одной из стороны равна 3 см. Значит, чтобы узнать, чему равна длина второй стороны , нужно из общей длины двух сторон вычесть длину известной стороны.
8 см – 3 см = 5 см – длина второй стороны.
Начертим прямоугольник.
Получается, необходимо начертить прямоугольник со сторонами 3 см и 5 см.
Номер 26.
Собрали 18 кг вишни. Из них взяли на компот 3 кг вишни, а на варенье в 4 раза больше, чем на компот. Составь различные выражения и объясни, что они обозначают.
Ответ:3 ∙ 4 – сколько взяли вишни на варенье. 18 − (3 + 3 ∙ 4) – сколько вишни осталось 3 + 3 ∙ 4 – сколько взяли вишни на компот и варенье.
«в 4 раза больше», значит, вычисляется умножением.
Оформляем условие в виде краткой записи.
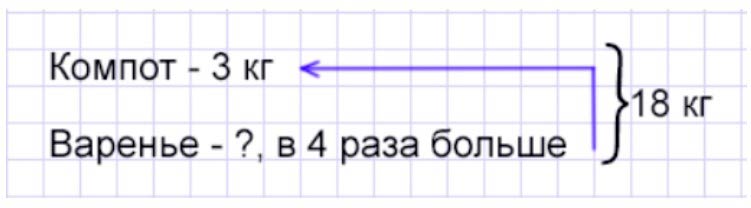
Рассуждаем.
Собрали 18 кг вишни, а взяли – 3 кг на компот и некоторое количество на варенье. На варенье потратили в 4 раза больше ягоды, чем на компот. Значит, чтобы узнать, сколько вишни потратили на варенье, нужно умножить количество ягоды на компот на 4.
3 · 4 – выражение для вычисления количества вишни на ягоды.
Продолжаем рассуждение.
Общее количество потраченной ягоды складывается из количества ягоды, потраченной на варенье и компот. Значит, чтобы узнать, сколько ягоды потратили всего, нужно сложить количество ягоды на компот и варенье.
3 + 3 · 4 – выражение для вычисления количества потраченной ягоды.
Продолжаем рассуждение.
Общее количество собранной вишни складывается из количества потраченной вишни и оставшейся. Значит, чтобы узнать, сколько ягоды осталось, нужно из общего количества вишни вычесть количество потраченной.
18 – (3 + 3 · 4) – выражение для вычисления количества оставшейся ягоды.
Оформляем задание в тетрадь.
3 ∙ 4 = 12 (кг) − вишни взяли на варенье.
3 + 3 ∙ 4 = 3 + 12 = 15 (кг) − взяли на компот и варенье.
18 − (3 + 3 ∙ 4) = 18 − 15 = 3 (кг) – осталось ягоды.
Номер 27.
Тетрадь стоит 8 р., а книга – в 4 раза дороже, чем тетрадь. На сколько рублей тетрадь дешевле, чем книга?
Ответ:

1-й способ решения:
1) 8 ∙ 4 = 32 (руб.) – стоит книга.
2) 32 − 8 = 24 (руб.)
Ответ: тетрадь дешевле книги на 24 рубля.
2-й способ решения: 8∙ 4 – 8 = 32 – 8 = 24 (руб.) – на сколько меньше. Ответ: на 24 рубля.
1) «в 4 раза больше», значит, вычисляется умножением.
2) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
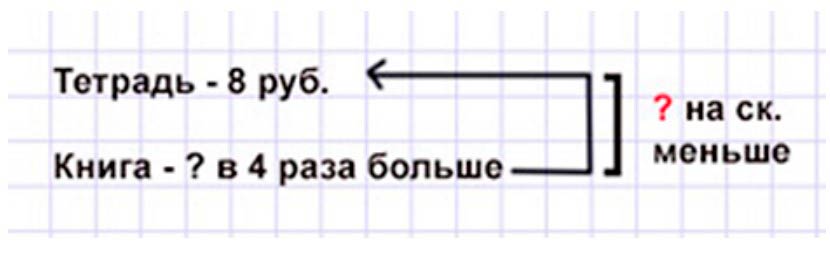
Рассуждаем.
Тетрадь стоит 8 рублей, а книга – в 4 раза дороже. Значит, чтобы узнать, сколько стоит книга, нужно стоимость тетради умножить на 4.
8 ∙ 4 = 32 (руб.) – стоит книга.
Продолжаем рассуждение.
Тетрадь стоит 8 рублей, а книга – 32 рубля. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее, значит из стоимости книги вычесть стоимости тетради.
32 − 8 = 24 (руб.) – на сколько тетрадь дешевле книги.
Записываем ответ.
Ответ: тетрадь дешевле книги на 24 рубля.
Решение выражением:
8 · 4 – 8 = 24 (руб.).
Номер 28.
Начерти четырехугольник, в котором 2 прямых угла, один тупой и один острый угол.
Ответ:
Помни о том, что угол – геометрическая фигура, стороны которой лежат на лучах, выходящих из одной точки.
Рассуждаем.
Помни о видах углов:
Прямой – угол, градусная мера которого – 90 градусов.
Острый – угол, градусная мера которого меньше 90 градусов.
Тупой – угол, градусная мера которого меньше тупого, но больше прямого.
Начертим четырёхугольник.
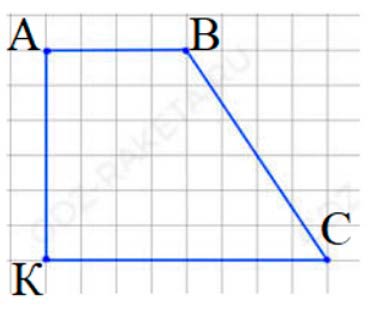
АВСК – четырёхугольник, где:
ВАК = АКС – прямые углы.
АВС – тупой угол.
ВСК – острый угол.
Номер 29.
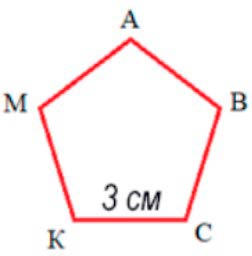
Из куска проволоки сначала сделали треугольник, как на рисунке, а затем пятиугольник с равными сторонами. Найди длину стороны пятиугольника.

1-й способ решения: 1) 6 + 7 + 2 = 15 (см) – периметр треугольника. 2) 15 : 5 = 3 (см) Ответ: длины сторон пятиугольника равна 3 см.
2-й способ решения: (6 + 7 + 2) : 5 = 15 : 5 = 3 см – длина стороны пятиугольника. Ответ: 3 см.
1) Треугольник – геометрическая фигура, многоугольник у которого 3 угла и три стороны.
2) Пятиугольник – геометрическая фигура, многоугольник у которого 5 углов и пять сторон.
Рассуждаем.
Треугольник – замкнутая ломаная. Длина ломаной – сумма длин всех отрезков-звеньев, а периметр треугольника – сумма длин всех его сторон. Значит, чтобы узнать, каков периметр треугольника, нужно измерить длины всех отрезков, а полученные значения сложить.
Измерим длинны сторон треугольника.
1 сторона – 6 см,
2 сторона – 7 см,
3 сторона – 2 см.
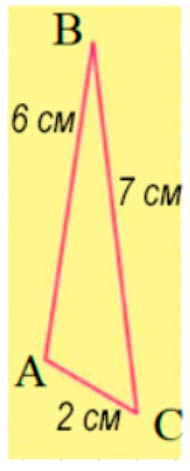
Найдём периметр треугольника.
Чтобы найти периметр треугольника нужно все стороны треугольника сложить.
6 см + 7 см + 2 см = 15 см – периметр треугольника.
Продолжаем рассуждение.
Нам нужно найти сторону пятиугольника, у которого периметр равен 15 см. Данный пятиугольник с равными сторонами, значит, чтобы найти длину стороны нужно периметр разделить на количество сторон.
15 : 5 = 3 (см) – длина стороны пятиугольника.
Номер 30.
Мальчик вошел в лифт на третьем этаже и, проехав 2 этажа, вышел из лифта. На каком этаже мальчик мог выйти из лифта?
Ответ:1) 3 + 2 = 5 (эт.) – мог выйти мальчик. 2) 3 − 2 = 1 (эт.) – мог выйти мальчик. Ответ: на 5 этаже и на 1 этаже мог выйти мальчик из этого лифта.
Лифт – устройство, позволяющее жителям многоквартирных домов передвигаться быстро между этажами: подниматься на некоторую высоту и опускаться.
Рассмотрим случай, когда лифт поехал вверх.
Проиллюстрируем:
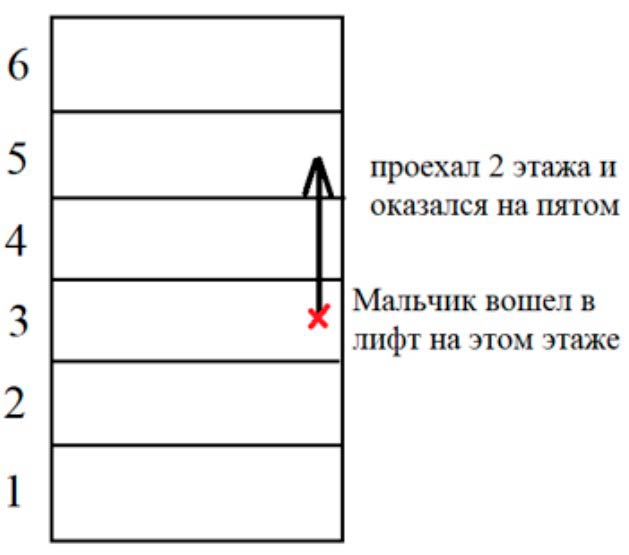
Значит мальчик вышел на 5 этаже.
Рассмотрим случай, когда лифт поехал вниз.
Проиллюстрируем:
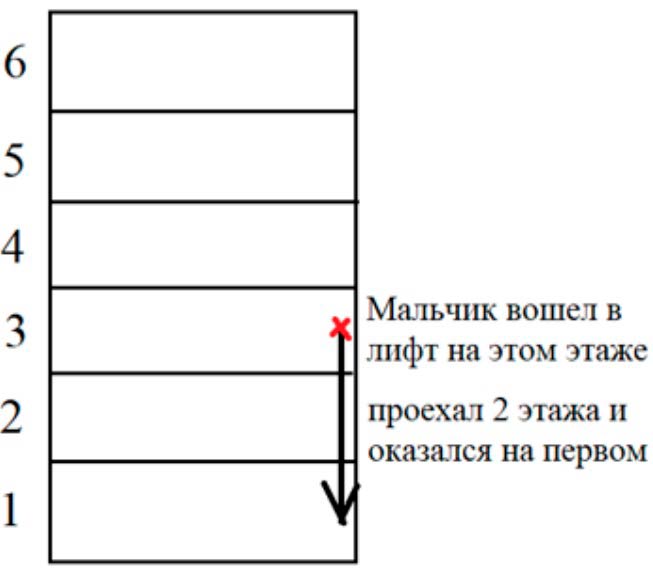
Значит мальчик вышел на 1 этаже.
Оформляем задание в тетрадь.
Возможно, что проехать 2 этажа можно вверх или вниз.
1 вариант:
3 + 2 = 5 (эт.) – мог выйти мальчик.
2 вариант:
3 − 2 = 1 (эт.) – мог выйти мальчик.
Ответ: на 5 этаже или на 1 этаже.
Задание внизу страницы
Номер 6.
В строительном отряде было 19 юношей и 9 девушек. Они разбились на бригады по 7 человек. Сколько получилось бригад?
Ответ:
1) 19 + 9 = 28 (чел.) – было в строительном отряде.
2) 28 : 7 = 4 (бр.)
Ответ: 4 бригады получилось.
Данная задача: вида «кол-во человек в бригаде, кол-во бригад, общее кол-во человек» характеризуется зависимостями между компонентами:
Кол-во человек в бригаде · кол-во бригад = общее кол-во человек.
Общее кол-во человек : кол-во бригад = кол-во человек в бригаде.
Общее кол-во человек : кол-во человек в бригаде = кол-во бригад.
Оформляем условие в виде таблицы.
Общее количество человек в отряде – неизвестно, но известно, что 19 юношей и 9 девушек, а количество человек в одной бригаде – 7 человек. Неизвестно количество бригад. Заполняю всеми имеющимися данными таблицу:
.jpg)
Рассуждаем.
Общее количество человек в студенческом строительном отряде складывается из количества юношей и девушек. Соответственно, чтобы узнать, сколько было всего людей, нужно сложить количества юношей и девушек.
19 + 9 = 28 (чел.) – было в студенческом отряде.
Продолжаем рассуждение.
Количество человек, работающих в одной бригаде одинаковое, значит, чтобы узнать, сколько бригад получилось, нужно общее количество человек разделить на количество человек в одной бригаде.
28 : 7 = 4 (бр.) – всего бригад.
Записываем ответ.
Ответ: 4 бригады получилось.
Решение выражением: (19 + 9) : 7 = 4 (бр.)
Номер 7.
Составь задачи по выражениям.
1) 3 ∙ 8 + 6
2) 5 ∙ 4 - 15
Задача 1:
Миша купил 8 конфеты по 3 рублей за штуку и вафлю за 6 р. Сколько Миша истратил денег?

Ответ: 30 рублей истратил Миша на покупки.
Задача 2:
Ручка стоит 15 р., ластик – 5 рублей, а тетрадь в 4 раза дороже ластика. На сколько рублей тетрадь стоит дороже ручки?

Ответ: на 5 рублей тетрадь стоит дороже ручки.
1) Задача 1: Миша купил 8 конфеты по 3 рублей за штуку и вафлю за 6 р. Сколько Миша истратил денег?
2) Задача 2: Ручка стоит 15 р., ластик – 5 рублей, а тетрадь в 4 раза дороже ластика. На сколько рублей тетрадь стоит дороже ручки?
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
Миша купил 8 конфет по 3 рубля за штуку. Значит, нам известна цена, количество, но неизвестна общая стоимость покупки. При этом общая стоимость покупки складывается из стоимости всех конфет. Значит, чтобы узнать, сколько стоят все конфеты, нужно их стоимости сложить.
Но цена конфет одинаковая, значит заплатили равное количество денег. Значит, сложением одинаковых слагаемых можно заменить умножением.
3 · 8 = 24 (руб.) – стоимость 8 конфет.
Продолжаем рассуждение.
Общая стоимость покупки складывается из стоимости вафли и конфет. Поэтому, чтобы узнать, сколько стоит вся покупка, нужно сложить стоимости конфет и вафли.
24 + 6 = 30 (руб.) – стоимость покупки.
Записываем ответ.
Ответ: 30 рублей истратил Миша.
Решение выражением:
3 ∙ 8 + 6 = 30 (руб.)
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
Ластик стоит 5 рублей, а тетрадь – в 4 раза дороже ластика. Значит, тетрадь стоит 4 раза по тому, сколько стоит ластик. Поэтому, чтобы узнать, сколько стоит тетрадь, нужно стоимость ластика умножить на 4.
5 · 4 = 20 (руб.) – стоимость тетради.
Продолжаем рассуждение.
Тетрадь стоит 20 рублей, а ручка – 15 рублей. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. То есть, чтобы узнать, на сколько дороже стоит тетрадь, нужно из стоимости тетради вычесть стоимости ручки.
20 – 15 = 5 (руб.) – на сколько тетрадь дороже ручки.
Записываем ответ.
Ответ: на 5 рублей тетрадь дороже ручки.
Решение выражением:
5 ∙ 4 – 15 = 5 (руб.)
Номер 8.
63 : 7 9 ∙ 7
56 : 8 6 ∙ 6
48 : 8 7 ∙ 7
8 ∙ 3 - 3 ∙ 8
7 ∙ 6 - 6 ∙ 7
4 ∙ 8 - 8 ∙ 3
54 - 24 : 6 + 40
90 - 21 + 42 : 7
35 - 30 : 5 + 25
63 : 7 = 9 9 ∙ 7 = 63
56 : 8 = 7 6 ∙ 6 = 36
48 : 8 = 6 7 ∙ 7 = 49

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7.
Выполним деление.
63 : 7 = 9,
так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
56 : 8 = 7,
так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
48 : 8 = 6,
так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 количество одинаковых слагаемых.
Выполним умножение.
9 · 7 = 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
1 3 2
8 · 3 − 3 · 8 = 0
1) 8 ∙ 3 = 24
2) 3 ∙ 8 = 24
3) 24 − 24 = 0
1 3 2
7 ∙ 6 − 6 ∙ 7 = 0
1) 7 ∙ 6 = 42
2) 6 ∙ 7 = 42
3) 42 − 42 = 0
1 3 2
4 ∙ 8 − 8 ∙ 3 = 8
1) 4 ∙ 8 = 32
2) 8 ∙ 3 = 3 · 8 = 24
3) 32 − 24 = 8
2 1 3
54 − 24 : 6 + 40 = 90
1) 24 : 6 = 4
2) 54 – 4 = 50
3) 50 + 40 = 90
2 1 3
90 – 21 + 42 : 7 = 75
1) 42 : 7 = 6
2) 90 – 21 = 90 – (20 + 1) = (90 – 20) – 1 = 70 – 1 = 69
3) 69 + 6 = 69 + (1 + 5) = (69 + 1) + 5 = 70 + 5 = 75
2 1 3
35 – 30 : 5 + 25 = 54
1) 30 : 5 = 6
2) 35 – 6 = 35 – (5 + 1) = (35 – 5) – 1 = 30 – 1 = 29
3) 29 + 25 = 29 + (1 + 24) = (29 + 1) + 24 = 30 + 24 = 54
Оформляем задание в тетрадь.
63 : 7 = 9
56 : 8 = 7
48 : 8 = 6
9 ∙ 7 = 63 6 ∙ 6 = 36 7 ∙ 7 = 49
8 · 3 – 3 · 8 = 0, так как 8 · 3 = 3 · 8, по переместительному свойству умножения.
7 · 6 – 6 · 7 = 0, так как 7 · 6 = 6 · 7, по переместительному свойству умножения.
4 · 8 – 8 · 3 = 32 – 24 = 8
54 – 24 : 6 + 40 = 54 – 4 + 40 = 50 + 40 = 90
90 – 21 + 42 : 7 = 90 – 21 + 6 = 69 + 6 = 75
35 – 30 : 5 + 25 = 35 – 6 + 25 = 29 + 25 = 54
Номер 9.
Начерти на клетчатой бумаге и вырежи прямоугольник и два треугольника, как на чертеже.
Составь из этих фигур четырёхугольник; пятиугольник.

Четырехугольник.

Пятиугольник.

1) Четырехугольник – фигура, у которой четыре угла.
2) Треугольник – фигура, у которой три угла.
3) Пятиугольник – фигура, у которой 5 углов.
Начертим и вырежем фигуры.
Начерти квадрат со стороной 2 см. Внутри квадрата проведи диагональ слева направо. Вырежи квадрат и разрежь его на два треугольника по диагонали.
Начерти прямоугольник со сторонами 4 см и 2 см, вырежи его.
-(2023).jpg)
Составим четырёхугольник.
Четырёхугольник из данных фигур можно составить несколькими способами:
Способ 1. К одной из сторон прямоугольника подставь квадрат из двух треугольников и получится прямоугольник со сторонами 6 см и 2 см.
-(2023).jpg)
Способ 2. Раздели квадрат на два равных треугольника по диагонали и подставь их к прямоугольнику по разным сторонам. Треугольники ты можешь повернуть в любую сторону.
-(2023).jpg)
Составим пятиугольник.
Два треугольника подставь к прямоугольнику сверху или снизу, как крыша у домика и получится пятиугольник.
-(2023).jpg)
Задание внизу страницы.
Сосчитай, сколько квадратных сантиметров в каждой фигуре (задание 9, рис. 1, 2).
Ответ:В красном квадрате 4 см2.
В зелёном прямоугольнике 8 см2.
1) Площадь фигуры – часть плоскости, которая ограничена линией и которую, занимает фигура.
2) Чтобы узнать площадь фигуры, нужно сосчитать количество клеток плоскости.
3) Площадь фигуры вычисляется в квадратных сантиметрах.
Рассуждаем.
Рассмотрим розовую фигуру. Разделим фигуру на квадратики со сторонами 1 см и посчитаем количество квадратиков.
-(2023).jpg)
Площадь одного квадратика со стороной 1 см равна 1 см2.
Таких квадратиков получилось 4.
1 · 4 = 4 (см2)
Значит площадь квадрата равна 4 см2.
Продолжаем рассуждение.
Рассмотрим зелёную фигуру. Разделим фигуру на квадратики со сторонами 1см и посчитаем количество квадратиков.
-(2023).jpg)
Площадь одного квадратика со стороной 1 см равна 1 см2.
Таких квадратиков в прямоугольнике 8.
1 · 8 = 8 (см2)
Значит площадь прямоугольника 8 см2.
Записываем ответ.
Ответ: Площадь кварата – 4 см2, площадь прямоугольника – 8 см2.
Задание на полях страницы.
Начерти:


Ось симметрии – это линия, по которой можно сложить так, что она разобьется на две равные части, которые при наложении совпадут, а значит, имеют равные площади.
Начертим фигуру.
Фигура состоит из 6 квадратов со сторонами 1 см и 4 ромбом.
-(2023).jpg)
Найдём оси симметрии.
В данной фигуре две оси симметрии – горизонтальная и вертикальная.
На рисунке ось симметрии показана синей линией. Если чертёж согнуть по оси симметрии, то рисунки совпадут.
-(2023).jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.