Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 54

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 17.
В цирковом представлении участвовали 3 собачки, а голубей было в 4 раза больше. На сколько больше было голубей, чем собачек?
Ответ:

1-й способ решения:
1) 3 ∙ 4 = 12 (шт.) – голуби.
2) 12 − 3 = 9 (шт.)
Ответ: голубей было на 9 больше, чем собачек.
2-й способ решения: 3 ∙ 4 – 3 = 12 – 3 = 9 (шт.) – на столько больше Ответ: на 9 голубей больше.
1) «в 3 раза больше», значит, вычисляется умножением.
2) «на ? больше», значит, вычисляется вычитанием.
Оформляем условие в виде краткой записи.
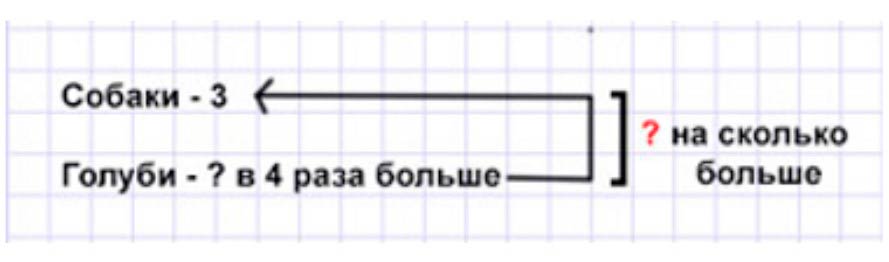
Рассуждаем.
В представлении участвовали 3 собачки, а голубей было в 4 раза больше. В 4 раза больше, значит, 4 раза по количеству собачек. Соответственно, чтобы узнать, сколько голубей участвовало в представлении, нужно количество собачек умножить на 4.
3 · 4 = 12 (шт.) – голуби.
Продолжаем рассуждение.
В представлении участвовали 3 собачки и 12 голубей. Чтобы узнать, на сколько больше было голубей, чем собачек, нужно вычесть из большего количества меньшее, значит из количества голубей нужно вычесть количество собачек.
12 − 3 = 9 (шт.) – на сколько голубей больше, чем собак.
Записываем ответ.
Ответ: на 9 голубей больше.
Решение выражением:
3 · 4 – 3 = 9 шт.
Номер 18.
В хоре «Мисолька» 15 дошкольников, учеников начальной школы на 7 больше, а старшеклассников столько, сколько дошкольников и учеников начальной школы вместе. Сколько ...?
Ответ:Сколько старшеклассников было в хоре?

1) 15 + 7 = 22 (чел.) – начальная школа. 2) 15 + 22 = 37 (чел.) Ответ: 37 старшеклассников в хоре.
1) «на 7 больше», значит, вычисляется сложением.
2) Вопрос: Сколько старшеклассников было в хоре?
Оформляем условие в виде краткой записи.
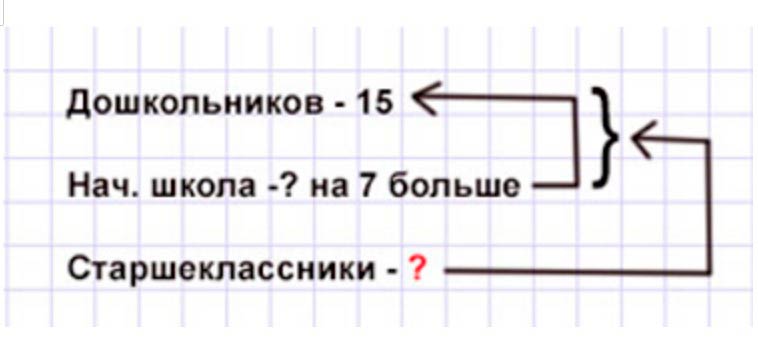
Рассуждаем.
В хоре было 15 дошкольников, а учеников начальной школы на 7 больше. Значит, что учеников начальной школы было столько, сколько дошкольников и еще 7 учеников. Получается, чтобы узнать, сколько было учеников начальной школы, нужно к количеству дошкольников прибавить 7 учеников.
15 + 7 = 22 (чел.) – начальная школа.
Продолжаем рассуждение.
Старшеклассников было столько, сколько дошкольников и учеников начальной школы вместе. Значит, чтобы узнать, сколько было старшеклассников, нужно сложить количество дошкольников и учеников начальной школы.
15 + 22 = 37 (чел.) – старшеклассники.
Записываем ответ.
Ответ: 37 старшеклассников в хоре.
Решение выражением:
15 + (15 + 7) = 37 (чел.).
Номер 19.
2 механика открыли автомастерскую. В день они ремонтировали по 3 машины. Сколько машин они отремонтировали за 6 дней?
Ответ:
1 день – 2 чел. по 3 м.
6 дней – ? м.
1-й способ решения:
1) 2 ∙ 3 = 6 (м.) – ремонтировали в день оба механика.
2) 6 ∙ 6 = 36 (м.)
Ответ: 36 машин отремонтировали за 6 дней.
2-й способ решения: 2 ∙ 3 ∙ 6 = 6 ∙ 6 = 36 (м.) – отремонтировали за 6 дней. Ответ: 36 машин.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в краткой записи.
1 день – 2 чел. по 3 м.
6 дней – ? м.
Рассуждаем.
2 механика в день ремонтировали по 3 машины. Значит, чтобы узнать, сколько всего машин они ремонтировали за день, нужно сложить количество отремонтированных машин обоими механиками.
Но каждый механик ремонтировал одинаковое количество машин. Поэтому, сложение одинаковых слагаемых можно заменить умножением.
3 · 2 = 6 (м.) – ремонтировали в день оба механика.
Продолжаем рассуждение.
Получается, за день они ремонтируют 6 машин, а за 6 дней – неизвестное количество. При этом, общее количество отремонтированных машин складывается из количества машин, отремонтированных в каждый из дней. Соответственно, нужно сложить все отремонтированные машины в каждый из 6 дней.
Но количество отремонтированных машин в каждый из дней одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением.
6 · 6 = 36 (м.) - отремонтировали за 6 дней.
Запишем ответ.
Ответ: 36 машин отремонтируют за 6 дней.
Решение выражением:
(2 · 3) · 6 = 36 (м.).
Номер 20.
1) На сколько 36 больше, чем 4; 6; 9?
Во сколько раз 36 больше, чем 4; 6; 9?
2) На сколько 10 меньше, чем 80; 90; 100?
Во сколько раз 10 меньше, чем 80; 90; 100?
1) 36 − 4 = 32 – на 32
36 − 6 = 30 – на 30
36 − 9 = 27 – на 27
36 : 4 = 9 – в 9 раз
36 : 6 = 6 – в 6 раз
36 : 9 = 4 – в 4 раз
2) 80 − 10 = 70 – на 70
90 − 10 = 80 – на 80
100 − 10 = 90 – на 90
80 : 10 = 8 – в 8 раз
90 : 10 = 9 – в 9 раз
100 : 10 = 10 – в 10 раз
1) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
3) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
4) Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Рассмотрим задание 1.
Узнаем на сколько 36 больше, чем:
Число 4:
36 – 4 = 30 + (6 – 4) = 30 + 2 = 32
Число 36 больше числа 4 на 32.
Число 6:
36 – 6 = 30 + (6 – 6) = 30 + 0 = 30
Число 36 больше числа 6 на 30.
Число 9:
36 – 9 = 36 – (6 + 3) = (36 – 6) – 3 = 30 – 3 = 27
Число 36 больше числа 9 на 27.
Узнаем во сколько раз 36 больше, чем:
Число 4:
36 : 4 = 9,
так как 4 · 9 = 36
Число 36 больше числа 4 в 9 раз.
Число 6:
36 : 6 = 6,
так как 6 · 6 = 36
Число 36 больше числа 6 в 6 раз.
Число 9:
36 : 9 = 4,
так как 4 · 9 = 36
Число 36 больше числа 9 в 4 раза.
Рассмотрим задание 2.
Узнаем на сколько 10 меньше, чем:
Число 80:
80 – 10 = 70
Число 10 меньше числа 80 на 70.
Число 90:
90 – 10 = 80
Число 10 меньше числа 90 на 80.
Число 100:
100 – 10 = 90
Число 10 меньше числа 100 на 90.
Во сколько раз 10 меньше, чем:
Число 80:
80 : 10 = 8
Число 10 меньше числа 80 в 8 раз.
Число 90:
90 : 10 = 9
Число 10 меньше числа 90 в 9 раз.
Число 100:
100 : 10 = 10
Число 10 меньше числа 100 в 10 раз.
Оформляем задание в тетрадь.
1)
36 − 4 = 32 – на 32
36 − 6 = 30 – на 30
36 − 9 = 27 – на 27
36 : 4 = 9 – в 9 раз
36 : 6 = 6 – в 6 раз
36 : 9 = 4 – в 4 раз
2)
80 − 10 = 70 – на 70
90 − 10 = 80 – на 80
100 − 10 = 90 – на 90
80 : 10 = 8 – в 8 раз
90 : 10 = 9 – в 9 раз
100 : 10 = 10 – в 10 раз
Номер 21.
1) Найди значение суммы d + 39, если d = 57, d = 8, d = 1 и d = 0.
2) Найди значение разности 65 − b, если b = 65, b = 60, b = 49, b = 6, b = 5 и b = 0.
1) d + 39
Если d = 57, то 57 + 39 = 96
Если d = 8, то 8 + 39 = 47
Если d = 1, то 1 + 39 = 40
Если d = 0, то 0 + 39 = 39
2) 65 – b
Если b = 65, то 65 − 65 = 0
Если b = 60, то 65 − 60 = 5
Если b = 49, то 65 − 49 = 16
Если b = 6, то 65 − 6 = 59
Если b = 5, то 65 − 5 = 60
Если b = 0, то 65 − 0 = 65
1) d + 39, значит, увеличить число на 39 единиц, т.е. вычисляется сложением.
2) 65 – b, значит, вычесть из числа 65 единиц, т.е. вычисляется вычитанием.
Рассуждаем.
d + 39, если:
d = 57, то 57 + 39 = 57 + (33 + 6) = (57 + 33) + 6 = 90 + 6 = 96
Число 39 разложим на сумму чисел 33 и 6. К числу 57 вначале прибавим число 33, а потом прибавим число 6.
d = 8, то 8 + 39 = (7 + 1) + 39 = (39 + 1) + 7 = 40 + 7 = 47
Число 8 разложим на сумму чисел 1 и 7. К числу 39 вначале прибавим число 1, а потом прибавим число 7.
d = 1, то 1 + 39 = 30 + (1 + 9) = 30 + 10 = 40
Единицы сложим с единицами, а десятки с десятками.
0 + 39 = 39
Если к числу прибавить нуль, то число не изменится.
Оформляем задание в тетрадь.
d + 39, если:
d = 57, то 57 + 39 = 96
d = 8, то 8 + 39 = 47
d = 1, то 1 + 39 = 40
d = 0, то 0 + 39 = 39
Рассуждаем.
65 – b, если:
b = 65, то 65 – 65 = 0
Если из числа вычесть само число, то получится нуль.
b = 60, то 65 – 60 = (60 – 60) + 5 = 0 + 5 = 5
Десятки вычитаем из десяток, а единицы вычитаем из единиц.
b = 49, то 65 – 49 = 65 – (45 + 4) = (65 – 45) – 4 = 20 – 4 = 16
Число 49 разложим на сумму чисел 45 и 4. Вначале из числа 65 вычтем число 45, а потом вычтем число 4.
b = 6, то 65 – 6 = 65 – (5 + 1) = (65 – 5) – 1 = 60 – 1 = 59
Число 6 разложим на сумму чисел 5 и 1. Вначале из числа 65 вычтем число 5, а потом вычтем число 1.
b = 5, то 65 – 5 = 60 + (5 – 5) = 60 + 0 = 60
Десятки вычитаем из десяток, а единицы вычитаем из единиц.
b = 0, то 65 – 0 = 65
Если из числа вычесть нуль, то число не изменится.
Оформляем задание в тетрадь.
65 – b, если:
b = 65, то 65 − 65 = 0
b = 60, то 65 − 60 = 5
b = 49, то 65 − 49 = 16
b = 6, то 65 − 6 = 59
b = 5, то 65 − 5 = 60
b = 0, то 65 − 0 = 65
Номер 22.
Начерти два отрезка так, чтобы длина одного была 4 см, а длина другого – в 3 раза больше. Обозначь отрезки буквами и узнай, на сколько сантиметров один из них короче другого.
Ответ:1) 4 ∙ 3 = 12 (см) – длина второго отрезка. 2) 12 − 4 = 8 (см) Ответ: отрезок АВ на 8 см короче отрезка CD.

1) Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками. Отрезок имеет длину, т.е расстояние от точки до точки.
2) В 3 раза больше, значит, вычисляется умножением.
3) «на ? меньше», значит, вычисляется вычитанием.
Оформляем условие в виде краткой записи.
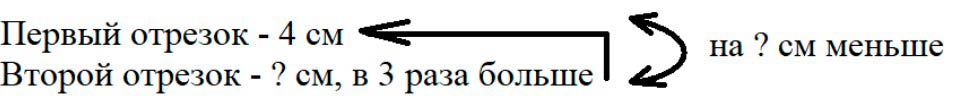
Рассуждаем.
Длина первого отрезка – 4 см, а второго неизвестна, но она в 3 раза больше, чем первого. Значит, чтобы узнать, какова длина второго отрезка, нужно длину первого отрезка умножить на 3.
4 ∙ 3 = 12 (см) – длина второго отрезка.
Продолжаем рассуждение.
Длина первого отрезка – 4 см, а второго – 12 см. Чтобы узнать, на сколько сантиметров длина одного отрезка меньше, чем длина большего, нужно из длины большего отрезка вычесть длину меньшего.
12 − 4 = 8 (см) – на сколько первый отрезок короче первого.
Начертим отрезки.
Начертим отрезок АВ = 4 см и отрезок СК = 12 см.
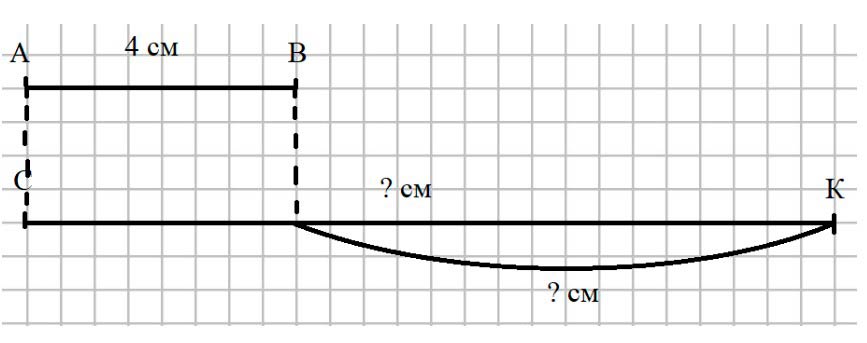
Записываем ответ.
Ответ: отрезок АВ на 8 см короче отрезка CD.
Решение выражением:
4 · 3 – 4 = 8 (см).
Задание на полях страницы
Цепочка:

Ответ:
24 − 6 = 18 18 + 7 = 25 25 : 5 = 5 5 ∙ 9 = 45
1) Выполни действия по порядку.
2) Первая красная шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
24 – 6 = 24 – (4 + 2) = (24 – 4) – 2 = 20 – 2 = 18
Число 6 разложим на сумму чисел 4 и 2. Вначале из числа 24 вычтем число 4, а потом вычтем число 2.
18 + 7 = 18 + (2 + 5) = (18 + 2) + 5 = 20 + 5 = 25
Число 7 разложим на сумму чисел 2 и 5. Вначале к числу 18 прибавим число 2, а потом прибавим число 5.
25 : 5 = 5,
так как 5 · 5 = 25.
5 · 9 = 45,
где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
24 − 6 = 18
18 + 5 = 25
25 : 5 = 5
5 ∙ 9 = 45
24 - 6 = 18 → 18 + 5 = 25 → 25 : 5 = 5 → 5 · 9 = 45
Квадратный сантиметр
Будем учиться измерять площади фигур в квадратных сантиметрах.
Площадь квадрата сторона которого 1 см, – это единица площади – квадратный сантиметр.
Слова «квадратный сантиметр» при числах записывают так: 4 см2, 12 см2.

В прямоугольнике АВСD поместилось 7 квадратных сантиметров. Значит, площадь прямоугольника АВСD равна 7 см2.
Номер 1.
Сосчитай, сколько квадратных сантиметров в каждой фигуре. Сравни площади этих фигур.

1 ф. – 8 см2
2 ф. – 7 см2
Площадь первой фигуры больше площади второй фигуры.8 см2 > 7 см2
1) Площадь фигуры – часть плоскости, на которой она лежит. Чтобы узнать площадь фигуры, нужно посмотреть, из скольких одинаковых клеток она составлена.
2) Помни, что площадь фигуры выражается в квадратных сантиметрах.
Найдём площадь первой фигуры.
Голубая фигура имеет 8 одинаковых клеток. Значит площадь фигуры равна 8 см2, так как площадь оной клетки 1 см2.
1 · 8 = 8 (см2) – площадь голубой фигуры.
Найдём пощадь второй фигуры.
Розовая фигура имеет 7 олинаковых клеток. Значит площадь фигуры равна 7 см2 так как площадь оной клетки 1 см2.
1 · 7 = 7 (см2) – площадь розовой фигуры.
Сравниваем пощади фигур.
Чтобы узнать площадь какой фигуры больше, нужно сравнить числовые значения площадей.
8 см2 > 7 см2 – значит площадь голубой фигуры больше площади розовой фигуры.
Записываем ответ.
Ответ: площадь первой фигуры больше площади второй фигуры.
Номер 2.
Каждое из чисел 72, 56, 48, 64 уменьши на 40, а результат уменьши в 4 раза.
Ответ:
1) Уменьши на 40, значит, вычти 40, т.е. уменьши число на 40 единиц.
2) Уменьши в 4 раза, значит, раздели на 4.
Рассуждаем.
Уменьшить число на 40 – это значит из числа нужно вычесть 40.
Результат уменьшить в 4 раза. значит нужно разделить на 4.
Выражение для вычисления: (а – 40) : 4, где а – заданное число.
Вычисляем.
(а – 40) : 4, если:
а = 72, то (72 – 40) : 4 = 8
1) 72 – 40 = 32
2) 32 : 4 = 8
а = 56, то (56 – 40) : 4 = 4
1) 56 – 40 = 16
2) 16 : 4 = 4
а = 48, то (48 – 40) : 4 = 2
1) 48 – 40 = 8
2) 8 : 4 = 2
а = 64, то (64 – 40) : 4 = 6
1) 64 – 40 = 24
2) 24 : 4 = 6
Оформляем задание в тетрадь.
(72 – 40) : 4 = 32 : 4 = 8
(56 – 40) : 4 = 16 : 4 = 4
(48 – 40) : 4 = 8 : 4 = 2
(64 – 40) : 4 = 24 : 4 = 6
Номер 3.
Каждое из чисел 12, 20, 28, 36 уменьши в 4 раза, а результат увеличь в 7 раз.
Ответ:
1) Уменьшить в 4 раза, значит, разделить на 4.
2) Увеличить в 7 раз, значит, умножить на 7.
Рассуждаем.
Уменьшить число в 4 раза – это значит разделить число на 4.
Увеличить результат в 7 раз, значит умножить его на 7.
Выражение для вычисления: а : 4 · 7, где а – заданное число.
Вычислим.
а : 4 · 7, если:
а = 12, то 12 : 4 · 7 = 21
1) 12 : 4 = 3, так как 4 · 3 = 12
2) 3 · 7 = 21
а = 20, то 20 : 4 · 7 = 35
1) 20 : 4 = 5, так как 5 · 4 = 20
2) 5 · 7 = 35
а = 28, то 28 : 4 · 7 = 49
1) 28 : 4 = 7, так как 4 · 7 = 28
2) 7 · 7 = 49
а = 36, то 36 : 4 · 7 = 63
1) 36 : 4 = 9, так как 4 9 = 36
2) 9 · 7 = 7 · 9 = 63
Оформляем задание в тетрадь.
12 : 4 ∙ 7 = 3 ∙ 7 = 21
20 : 4 ∙ 7 = 5 ∙ 7 = 35
28 : 4 ∙ 7 = 7 ∙ 7 = 49
36 : 4 ∙ 7 = 9 ∙ 7 = 63
Номер 4.
На 4 дня лошади нужно 32 кг овса. (Ежедневная норма выдачи овса одна и та же.) Сколько килограммов овса нужно лошади на 6 дней, если норма выдачи в день не изменится?
Ответ:
1) 32 : 4 = 8 (кг) – на один день.
2) 8 ∙ 6 = 48 (кг)
Ответ: 48 кг овса нужно на 6 дней.
Данная задача: вида «расход на 1 день, количество дней, общий расход» характеризуется зависимостями между компонентами:
Расход на 1 день · количество дней = общий расход.
Общий расход : расход на 1 день = количество дней.
Общий расход : количество дней = расход на 1 день.
Для того, чтобы решить задачу, лучше разбить ее на две подзадачи:
Оформляем условие в виде таблицы .
На 4 дня лошади нужно 32 кг овса. Значит, известно количество дней и общий расход, но неизвестен расход в 1 день. Заполняю всеми известными данными таблицу:
-(2023).jpg)
Рассуждаем.
Расход овса в 1 день одинаковый. Значит, чтобы узнать, сколько овса расходуется в 1 день, нужно общий расход овса разделить на количество дней.
32 : 4 = 8 (кг) – на один день.
Оформляем условие в виде таблицы.
В первой задаче мы узнали, каков расход овса за 1 день. Теперь необходимо узнать, сколько кг овса нужно, чтобы кормить лошадь 6 дней. Значит, нам известен расход овса в 1 день и количество дней, а общий расход – нет. Заполняю всеми имеющимися данными таблицу:
-(2023).jpg)
Рассуждаем.
Общий расход овса на 6 дней складывается из количества овса, расходуемого в каждый из дней. Соответственно, чтобы узнать, сколько овса израсходовали за 6 дней, нужно сложить количества овса, расходуемы за 6 дней.
Но количество овса, расходуемое за 1 день одинаковое. Значит, сложение одинаковых слагаемых можно заменить умножением.
8 · 6 = 48 (кг) – на 6 дней.
Оформляем решение.
1) 32 : 4 = 8 (кг) – на один день.
2) 8 ∙ 6 = 48 (кг) – на 6 дней.
Записываем ответ.
Ответ: 48 кг овса нужно на 6 дней.
Решение выражением:
32 : 4 ∙ 6 = 8 ∙ 6 = 48 (кг)
Номер 5.
Из 21 кг свежей малины получается 3 кг сухой. Сколько взяли свежей малины, если получили 5 кг сухой?
Ответ:21 кг – 3 кг
? кг – 5 кг
1) 21 : 3 = 7 (кг) – чтобы получить 1 кг сухой.
2) 5 ∙ 7 = 35 (кг)
Ответ: 35 кг нужно взять свежей малины.
Данная задача: вида «расход на 1 день, количество дней, общий расход» характеризуется зависимостями между компонентами:
Расход на 1 день · количество дней = общий расход.
Общий расход : расход на 1 день = количество дней.
Общий расход : количество дней = расход на 1 день
Для того, чтобы решить задачу, лучше разбить ее на две подзадачи.
Оформляем условие в виде таблицы.
Из 21 кг свежей малины получают 7 кг сухой. Неизвестно, каково соотношение свежей и сухой малины.
Заполняю всеми известными данными из условия задачи таблицу:
-(2023).jpg)
Рассуждаем.
Из таблицы видно, что чтобы узнать соотношение между двумя состояниями малины, нужно количество свежей малины разделить на количество сухой.
21 : 3 = 7 (кг) – чтобы получить 1 кг сухой.
Оформляем условие в виде таблицы.
Соотношение сухой малины и свежей равно 7 кг, а количество сухой малины, которую получили равно 5 кг. Неизвестно, сколько свежей малины взяли, чтобы приготовить такое количество сухой. Заполняю всеми имеющимися данными таблицу:
-(2023).jpg)
Рассуждаю.
Из таблицы видно, что чтобы узнать, сколько свежей малины вязли для приготовления 5 кг сухой, нужно соотношение видов малин умножить на количество сухой малины.
5 · 7 = 35 (кг) – взяли малины для 5 кг сухой.
Оформляем условие в виде таблицы.
-(2023).jpg)
Оформляем решение.
1) 21 : 3 = 7 (кг) – чтобы получить 1 кг сухой.
2) 7 ∙ 5 = 35 (кг) – для 5 кг сухой.
Записываем ответ.
Ответ: 35 кг нужно взять свежей малины.
Решение выражением:
21 : 3 ∙ 5 = 35 (кг)
Задание на полях страницы.
Цепочка:

72 : 8 = 9
9 ∙ 4 = 36
36 + 6 = 42
42 : 7 = 6
1) Выполни действия по порядку.
2) Первая лиловая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
72 : 8 = 9, так как 8 · 9 = 72, где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 4 = 4 · 9 = 36, где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых. Применяем переместительное свойство умножения.
36 + 6 = 36 + (4 + 2) = (36 + 4) + 2 = 40 + 2 = 42
Разложим число 6 на сумму чисел 4 и 2. Вначале к числу 36 прибавим число 4, а потом прибавим число 2.
42 : 7 = 6, так как 6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
72 : 8 = 9
9 ∙ 4 = 36
36 + 6 = 42
42 : 7 = 6
b>72 : 8 = 9 → 9 · 4 = 36 → 36 + 6 = 42 → 42 : 7 = 6
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.