Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 48

Шаг 1.
Рассуждаем и выполняем вычисления.

7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

63 : 7 = 9,
так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

56 : 8 = 7,
так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

  1   2
4 · 6 : 8 = 3
1) 4 · 6 = 24
2) 24 : 8 = 3
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.

    1   2
54 : 6 · 5 = 45
1) 54 : 6 = 9
2) 9 · 5 = 5 · 9 = 45
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.

      1     2
(55 – 7) : 6 = 8
1) 55 – 7 = 55 – (5 + 2) = (55 – 5) – 2 = 50 – 2 = 48

2) 48 : 6 = 8
В данном выражении присутствуют действия вычитание и деление, а также скоби. Поэтому вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.

     2      1
28 : (32 – 25) = 4
1) 32 – 25 = 32 – (22 + 3) = (32 – 22) – 3 = 10 – 3 = 7

2) 28 : 7 = 4
В данном выражении присутствуют действия вычитание и деление, а также скоби. Поэтому вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.

Шаг 2.
Оформляем задание в тетрадь.

7 ∙ 8 = 56
7 ∙ 7 = 49

63 : 7 = 9
56 : 8 = 7

4 ∙ 6 : 8 24 : 8 = 3
54 : 6 ∙ 5 = 9 · 5 = 45
(55 − 7) : 6 = 48 : 6 = 8
28 : (32 − 25) = 28 : 7 = 4

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
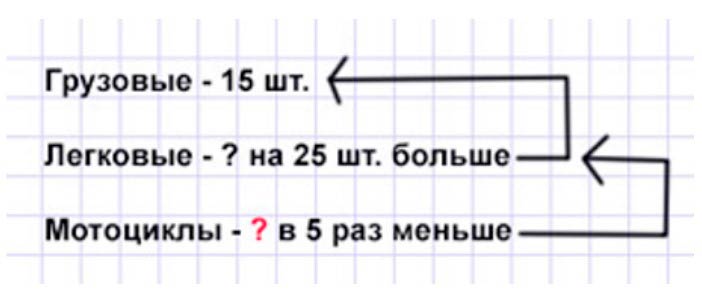
Рассуждаем.

На стоянке было 15 грузовых машин, а легковых – на 25 машин больше. Значит, что легковых машин было столько, сколько грузовых и еще 25 машин. Соответственно, чтобы узнать, сколько легковых машин было, нужно к количеству грузовых прибавить 25 машин.

1) 15 + 25 = 40 (шт.) – легковых машин было на стоянке.

Шаг 3.
Продолжаем рассуждение.

Мотоциклов было в 5 раз меньше, чем легковых машин. Значит, чтобы узнать, сколько мотоциклов было на стоянке, нужно количество легковых машин разделить на 5.

2) 40 : 5 = 8 (шт.) – было мотоциклов на стоянке.

Шаг 4.
Записываем ответ.

Ответ: 8 мотоциклов.

Решение выражением:
(15 + 25) : 5 = 8 (шт.).

Шаг 1.
Измерим отрезки.

Измерим отрезки с помощью линейки.

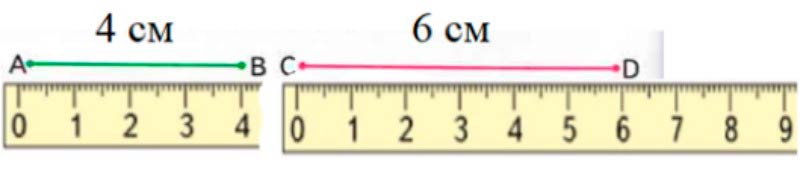
АВ = 4 см
CD = 6 см

Шаг 2.
Оформляем условие в виде краткой записи.

Шаг 3.
Рассуждаем.

Длина отрезка АВ = 4 см, а отрезка которого нужно начертить – неизвестно, но он должен быть в 2 раза больше, чем отрезок АВ. В 2 раза больше, значит, 2 раза по длине отрезка АВ.
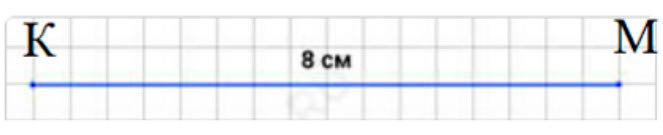
Соответственно, чтобы узнать, какова длина отрезка, нужно длину отрезка АВ умножить на 2. Назовем получившийся отрезок – отрезком КМ.

4 · 2 = 8 (см) – длина отрезка КМ.

Начертим отрезок КМ = 8 см с помощью линейки:

Шаг 4.
Продолжаем рассуждать.

Длина отрезка CD = 6 см, а отрезка которого нужно начертить – неизвестно, но он должен быть в 2 раза меньше, чем отрезок CD. В 2 раза меньше, значит половина от отрезка CD.
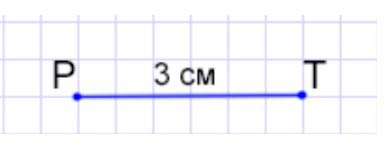
Соответственно, чтобы узнать, какова длина отрезка, нужно длину отрезка CD разделить на 2. Назовем получившийся отрезок – отрезком РТ.

6 : 2 = 3 (см) – длина отрезка РТ, так как 3 · 2 = 6.

Начертим отрезок РТ = 3 см с помощью линейки:

Шаг 5.
Оформляем задание в тетрадь.

Первый отрезок:
4 ∙ 2 = 8 (см) – длина отрезка, который в 2 раза больше АВ.

Второй отрезок:
6 : 2 = 3 (см) – длина отрезка, который в 2 раза меньше CD.

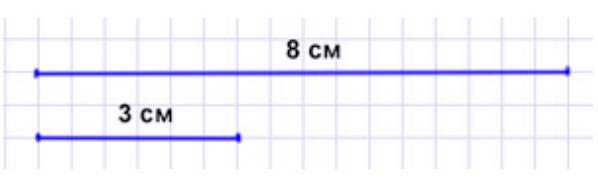
Ответ: 8 см и 3 см.

Шаг 1.
Оформляем условие в виде краткой записи.

Было – 8 л
Добавили – 40 л
Израсходовали – 25 л
Осталось – ? л

Шаг 2.
Рассуждаем.

В бензобаке было 8 литров бензина. Добавили 40 литров. Добавили, то есть бензина в баке стало на 40 литров больше. Соответственно, чтобы узнать, сколько бензина стало, нужно к количеству бензина прибавить количество добавленного.

8 + 40 = 48 (л) – после добавки бензина.

Шаг 3.
Продолжаем рассуждение.

После покупки израсходовали 25 литров бензина. Израсходовали, значит, его стало меньше. Поэтому, чтобы узнать, сколько бензина осталось, нужно из общего количества бензина вычесть количество истраченного.

48 − 25 = 23 (л) – бензина осталось в бензобаке.

Шаг 4.
Записываем ответ.

Ответ: 23 литра бензина.

Решение выражением:
(8 + 40) – 25 = 23 (л).

Шаг 1.
Рассмотрим фигуры.

Для удобства вычисления количества клеток в фигурах, разобьем фигуры на участки.

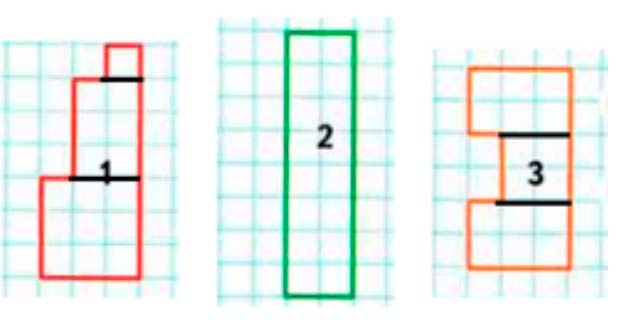
1 фигура состоит:
– из трёх строк по 3 клетки;
– из трёх строк по 2 клетки;
– одной клетки.

2 фигура состоит:
– из восьми строк по 2 клетки.

3 фигура состоит:
– из двух строк по 3 клетки;
– из двух строк по 2 клетки;
– из трёх строк по 3 клетки.

Шаг 2.
Вычислим.

Общее количество клеток складывается из количества клеток всех участков.

1 фигура:
3 · 3 + 3 · 2 + 1 = 9 + 6 + 1 = 16 (клеток).

2 фигура:
8 · 2 = 2 · 8 = 16 (клеток).

3 фигура:
2 · 3 + 2 · 2 + 2 · 3 = 6 + 4 + 6 = 16 (клеток).

Сравним количество клеток в фигурах:
16 кл. = 16 кл. = 16 кл.

Число клеток в фигурах одинаково.

Шаг 3.
Рассмотрим фигуры на симметрию.

Фигура 1 не имеет симметрию.

Фигура 2 имеет две оси симметрии – горизонтальную и вертикальную.

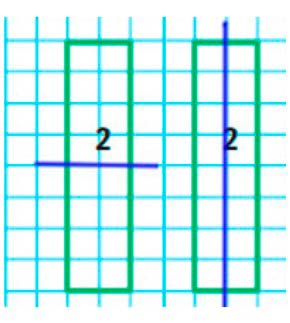
Фигура 3 имеет одну симметрию – горизонтальную.

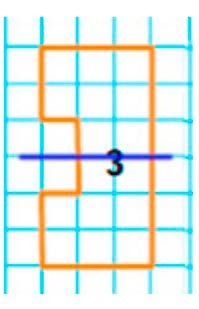
Вывод: фигуры 2 и 3 имеют ось симметрии.

Шаг 1.
Рассуждаем.

Сравним 6 · 2 + 6 · 4 и 6 · 6

Вычислим левую часть:
  1    3    2
6 · 2 + 6 · 4 = 12 + 24 = 36

Выражение состоит из действий сложение и умножение, поэтому вначале выполняем умножение по порядку слева направо, а потом сложение.

Вычислим правую часть:
6 · 6 = 36
Сравним: 36 = 36
Значит, 6 · 2 + 6 · 4 = 6 · 6

Сравним 7 · 3 – 3 · 2 и 3 · 4

Вычислим левую часть:
  1    3    2
7 · 3 – 3 · 2 = 21 – 6 = 15

Выражение состоит из действий вычитание и умножение, поэтому вначале выполняем умножение по порядку слева направо, а потом вычитание.

Вычислим правую часть:
3 · 4 = 12
Сравним: 15 > 12
Значит, 7 · 3 – 3 · 2 > 3 · 4

Сравним 35 : 5 + 10 : 5 и 45 : 5

Вычислим левую часть:
    1    3     2
35 : 5 + 10 : 5 = 7 + 2 = 9

Вычислим правую часть:
45 : 5 = 9
Сравним: 9 = 9
Значит, 35 : 5 + 10 : 5 = 45 : 5

Сравним 32 : 8 + 16 : 8 и 40 : 8

Вычислим левую часть:
    1    3     2
32 : 8 + 16 : 8 = 4 + 2 = 6

Вычислим правую часть:
40 : 8 = 5
Сравним: 6 > 5
Значит, 32 : 8 + 16 : 8 > 40 : 8

Шаг 2.
Запишем сравнение в тетрадь.

6 ∙ 2 + 6 ∙ 4 = 6 ∙ 6, так как 36 = 36
7 ∙ 3 − 3 ∙ 2 > 3 ∙ 4, так как 15 > 12
35 : 5 + 10 : 5 = 45 : 5, так как 9 = 9
32 : 8 + 16 : 8 > 40 : 8, так как 6 > 5

Шаг 1.
Рассуждаем.

а · 10 = 90
а – неизвестный множитель.
Подумай сколько раз нужно сложить число 10, чтобы получилось 90.
Число 10 нужно сложить 9 раз. Также сложение одинаковых слагаемых можно заменить умножением, поэтому число 10 нужно умножить на 9, чтобы получить 90.
а = 10

12 : b = 2
b – неизвестный делитель.
Вспомни таблицу умножения на 2. На какое число нужно умножить число 2, чтобы получить 12. Это число 6.
b = 6

х : 7 = 8
х – неизвестное делимое.
Вспомни таблицу умножения на 7. Какое число получится при умножении 7 на 8. Это число 56.
х = 56

Шаг 2.
Выполняем проверку.

а · 10 = 90
Проверка: вместо неизвестного а подставим число 9.
9 · 10 = 90
90 = 90 – верно.

12 : b = 2
Проверка: вместо неизвестного b поставим число 6.
12 : 6 = 2
2 = 2 – верно.

х : 7 = 8
Проверка: вместо неизвестного х подставим число 56.
56 : 7 = 8
8 = 8 – верно.

Шаг 3.
Оформляем задание в тетрадь.

а ∙ 10 = 90
а = 9

12 : b = 2
b = 6

х : 7 = 8
х = 56

Шаг 1.
Вычислим умножение.

9 · 7 = 7 · 9 = 63
Применяем переместительное свойство умножения и таблицу умножения на 7.

Шаг 2.
Вычислим деление.

49 : 7 = 7
так как 7 · 7 = 49
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

Шаг 3.
Расставляем порядок действий и выполняем вычисления.

    1    2
12 : 3 · 5 = 20
1) 12 : 3 = 4
2) 4 · 5 = 20

      1      2
(39 + 9) : 8 = 6
1) 39 + 9 = 39 + (8 + 1) = (39 + 1) + 8 = 40 + 8 = 48
2) 48 : 8 = 6

Шаг 4.
Оформляем задание в тетрадь.

9 ∙ 7 = 63
49 : 7 = 7
12 : 3 ∙ 5 = 4 · 5 = 20
(39 + 9) : 8 = 48 : 8 = 6