Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 40

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Вычисли и запомни!

5 ∙ 5 = 25 25 : 5 = 5 5 ∙ 6 = 30 6 ∙ 5 = 30 30 : 5 = 6 30 : 6 = 5 5 ∙ 7 = 35 7 ∙ 5 = 35 35 : 5 = 7 35 : 7 = 5 5 ∙ 8 = 40 8 ∙ 5 = 40 40 : 5 = 8 4 = 50 : 8 5 ∙ 9 = 45 9 ∙ 5 = 45 45 : 5 = 9 45 : 9 = 5
Номер 1.
Из чисел от 1 до 20 выпиши по порядку те, которые делятся без остатка на 5; на 4.
Ответ:Делятся на 5: 5, 10, 15, 20. Делятся на 4: 4, 8, 12, 16, 20.
1) Делятся без остатка на 5, т.е. нужно выписать числа, которые являются результатом умножения числа 5 на любые числа, т.е результаты таблиц умножения 5.
2) Делятся без остатка на 4, т.е. нужно выписать числа, которые являются результатом умножения 4 на любые числа, т.е результаты таблиц умножения 4.
Рассмотрим таблицу умножения на 5 до произведения 20.
5 · 1 = 5
5 · 2 = 10
5 · 3 = 15
5 · 4 = 20
Рассмотрим таблицу умножения на 4 до произведения 20.
4 · 1 = 4
4 · 2 = 8
4 · 3 = 12
4 · 4 = 16
4 · 5 = 20
Выпишем числа.
Полученные произведения и есть числа, которые делятся на 5, на 4.
Делятся без остатка на 5: 5, 10, 15, 20
Делятся без остатка на 4: 4, 8, 12, 16, 20
Номер 2.
Ответ:7 ∙ 5 = 35 45 : 9 = 5 24 : 8 = 3 5 ∙ 9 = 45 35 : 5 = 7 27 : 9 = 3

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
7 · 5 = 5 · 7 = 35
Применим переместительный закон и таблицу умножения на 5.
5 · 9 = 45
Применим таблицу умножения на 5.
45 : 9 = 5
Вспомним таблицу умножения.
Какое число при умножении на 9 даёт результат 45.
Это число 5, так как 5 · 9 = 45.
35 : 5 = 7
Вспомним таблицу умножения.
Какое число при умножении на 5 даёт результат 35.
Это число 7, так как 5 · 7 = 35.
24 : 8 = 3
Вспомним таблицу умножения.
Какое число при умножении на 8 даёт результат 24.
Это число 3, так как 3 · 8 = 24.
27 : 9 = 3
Вспомним таблицу умножения.
Какое число при умножении на 9 даёт результат 27.
Это число 3, так как 3 · 9 = 27.
3 · 9 + (21 – 4)
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действия в скобках – вычитание, потом умножение и последним действием – сложение.
18 : (16 – 17) · 2
В данном выражении присутствуют действия вычитание, умножение и деление, а также скобки. Вначале выполняем действия в скобках – вычитание, потом деление и последним действием – умножение.
Расставим порядок действий.
2 3 1
3 · 9 + (21 – 14)
2 1 3
18 : (16 – 17) · 2
Выполним письменное умножение.
7 · 5 = 5 · 7 = 35
5 · 9 = 45
45 : 9 = 5
35 : 5 = 7
24 : 8 = 3
27 : 9 = 3
2 3 1
3 · 9 + (21 – 4) = 44
1) 21 – 4 = 17
2) 3 ∙ 9 = 27
3) 27 + 17 = 44
2 1 3
18 : (16 – 7) · 2 = 4
1) 16 – 7 = 9
2) 18 : 9 = 2
3) 2 ∙ 2 = 4
Номер 3.
В куске было 24 м ткани. Из 10 м этой ткани сшили детские костюмы, а из остальной ткани – 7 одинаковых детских пальто. Сколько метров ткани израсходовали на одно пальто?
Ответ:
Всего – 24 м
Костюмы – 10 м
Пальто – 7 шт. по ? м
1-й способ решения:
1) 24 − 10 = 14 (м) – ткани осталось на 7 пальто.
2) 14 : 7 = 2 (м)
Ответ: 2 метра ткани расходовали на одно пальто.
2-й способ решения: (24 – 10) : 7 = 14 : 7 = 2 (м) – ткани израсходовали на одно пальто. Ответ: 2 метра.
Помни, что умножение – замена одинаковых слагаемых произведением, где:
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в виде краткой записи.
Всего – 24 м
Детские костюмы – 10 м
Пальто – 7шт. по ? м
Рассуждаем.
Общее количество ткани складывается из количества ткани, которая пошла на пошив костюмов и на пошив детских пальто. Поэтому, чтобы узнать, сколько метров ткани пошло на пошив пальто, нужно из общего количества ткани вычесть количество ткани на пошив костюмов.
24 − 10 = 14 (м) – ткани осталось на 7 пальто.
Продолжаем рассуждения.
Теперь нам известно, сколько всего ткани израсходовали на пошив 7 пальто, но неизвестен общий расход. А он одинаковый.
Чтобы узнать, сколько метров ткани израсходовали на пошив одного пальто, нужно общее количество ткани разделить на количество пальто.
14 : 7 = 2 (м) – ткани на одно пальто.
Записываем ответ.
Ответ: 2 метра.
Решение в виде выражения: (24 – 10) : 7 = 2 (м),
где 24 – 10 – количество ткани, израсходованной на пошив детских пальто.
Номер 4.
Из сетки с мячами взяли 4 мяча, и в ней еще осталось 12 мячей. На сколько мячей больше осталось, чем взяли?
Ответ:

12 − 4 = 8 (м.)
Ответ: на 8 мячей больше осталось, чем взяли.
«на ? больше», значит, вычисляется вычитанием.
Оформляем условие в виде краткой записи.
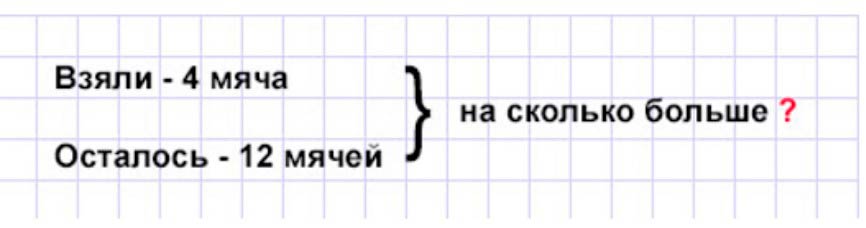
Рассуждаем.
Из сетки взяли 4 мяча, а осталось – 12 мячей. Поэтому, чтобы узнать, на сколько мячей больше осталось, чем взяли, нужно из большего количества мячей вычесть меньшее. Т.е. из количества мячей, которые остались, вычесть количество взятых мячей.
12 – 4 = 8 (м.)
Записываем ответ.
Ответ: на 8 мячей.
Номер 5.
В выражение b + 18 подставь вместо b число 0; 2; 5; 10. Запиши выражения и вычисли их значения. Наблюдай, как изменяются значения выражений.
Ответ:b + 18, если b = 0, то 0 + 18 = 18 b = 2, то 2 + 18 = 20 b = 5, то 5 + 18 = 23 b = 10, то 10 + 18 = 28 Второе слагаемое не меняется, а первое увеличивается, поэтому увеличивается и сумма.
Вычисление значений выражения сводится к применению правил:
Правило прибавления числа к сумме: (а + в) + с = (а + с) + в.
Правило прибавления суммы к числу: а + (в + с) = (а + в) + с.
Рассуждаем.
Вместо b нужно подставить данные числа.
b + 18, если:
b = 0, то 0 + 18 = 18
b = 2, то 2 + 18 = 2 + (10 + 8) = 10 + (2 + 8) = 10 + 10 = 20,
Использовали правило прибавления суммы к числу.
b = 5, то 5 + 18 = (2 + 3) + 18 = 3 + (2 + 18) = 20 + 3 = 23,
Использовали правило прибавления числа к сумме.
b = 10, то 10 + 18 = 10 + (10 + 8) = (10 + 10) + 8 = 20 + 8 = 28,
Использовали правило прибавления суммы к числу.
Делаем вывод.
Второе слагаемое неизменно, а первое увеличивается, поэтому увеличивается и сумма.
Оформляем задание в тетрадь.
b + 18, если:
b = 0, то 0 + 18 = 18
b = 2, то 2 + 18 = 20
b = 5, то 5 + 18 = 23
b = 10, то 10 + 18 = 28
Номер 6.
Футбольная команда провела 3 матча, забив в ворота соперника 3 мяча и пропустив в свои ворота 1 мяч. Первый матч команда выиграла, второй свела вничью, а третий проиграла. С каким счетом мог закончиться каждый матч?
Ответ:Первый матч – 0:3. Второй матч – 0:0. Третий матч – 1:0.
Подумай, с каким исходом может закончиться матч, чтобы понять, с каким счетом закончился каждый матч.
Разбираем возможные варианты.
В любом футбольном матче возможны три исход:
Победа: команда забила голов больше.
Проигрыш: команда забила голов меньше.
Ничья: забито командами равное количество голов.
Рассуждаем.
Футбольная команда провела 3 матча, при этом за все игры забили 3 раза, а пропустили – 1 мяч.
Первый матч: команда проиграла.
Значит, противоположная команда забила больше голов, чем сама команда, а так как команда пропустила только 1 мяч, значит счёт 1 : 0 в пользу команды противника.
Второй матч: ничья.
Ничья – это значит, что счет был равным.
А так как команда противников больше голов не забивала, значит счёт 0 : 0.
Третий матч: команда выиграла.
Значит команда забила больше мячей, чем команда соперников, а она забила 3 мяча, поэтому счёт 0 : 3.
Записываем ответ.
1−й матч: 1 : 0;
2−й матч: 0 : 0;
3−й матч: 0 : 3.
Задание внизу страницы
Ответ:8 ∙ 5 = 40 30 : 5 = 6 36 : 4 = 9

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5.
Рассуждаем.
8 · 5 = 5 · 8 = 40,
Применяем переместительное свойство умножения и таблицу умножения на 5.
30 : 5 = 6
Вспомним таблицу умножения на 5.
Какое число при умножении на 5 даёт результат 30.
Это число 6, так как 5 · 6 = 30.
36 : 4 = 9
Вспомним таблицу умножения на 4.
Какое число при умножении на 4 даёт результат 36.
Это число 9, так как 4 · 9 = 36.
6 · 5 + (40 – 18) = 52
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действия в скобках – вычитание, потом умножение и последним действием – сложение.
Расставим порядок действий.
2 3 1
6 · 5 + (40 – 18) = 52
Оформляем задание в тетрадь.
8 ∙ 5 = 40
30 : 5 = 6
36 : 4 = 9
2 3 1
6 · 5 + (40 – 18) = 52
1) 40 – 18 = 22
2) 6 ∙ 5 = 30
3) 30 + 22 = 52
Задание на полях страницы
Магический квадрат:

Ответ:

25 + 30 + 23 = 48 + 30 = 78
24 + 26 + 28 = 50 + 28 = 78
29 + 22 + 27 = 29 + 49 = 78
25 + 24 + 29 = 49 + 29 = 78
30 + 26 + 22 = 30 + 48 = 78
23 + 28 + 27 = 50 + 28 = 78
25 + 26 + 27 = 51 + 27 = 78
29 + 26 + 23 = 29 + 49 = 78
Магический квадрат – квадрат, в котором числа, стоящие на одной прямой по горизонтали, вертикали и диагонали в сумме образуют одинаковое число.
Узнаем магическую сумму.
Чтобы узнать магическую сумму, сложим числа по диагонали слева направо.
25 + 26 + 27 = 78 – магическая сумма.
В данном магическом квадрате по горизонтали, вертикали и диагонали сумма цифр должна равняться 78.
Рассмотрим первый столбец.
В столбце отсутствует второе число.
25 + + 29 = 78
Упростим выражение сложив числа 25 и 29.
54 + = 78
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 54 = 24 – недостающее число в первом столбце.
.jpg)
Рассмотрим вторую строчку.
В строчке отсутствует третье число.
24 + 26 + = 78
Упростим выражение сложив числа 24 и 26.
50 + = 78
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 50 = 28 – недостающее число во второй строке.
.jpg)
Рассмотрим третью строчку.
В строчке отсутствует второе число.
29 + + 27= 78
Упростим выражение сложив числа 29 и 27.
56 + = 78
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 56 = 22 – недостающее число во третьей строчке.
.jpg)
Рассмотри второй столбец.
В столбце отсутствует первое число.
+ 26 + 22 = 78
Упростим выражение сложив числа 26 и 22.
+ 48 = 78
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 48 = 30 – недостающее число во втором столбце.
.jpg)
Рассмотрим третью строчку.
В строке отсутствует первое число.
+ 28 + 27 = 78
Упростим выражение сложив числа 28 и 27.
+ 55 = 78
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 55 = 23 – недостающее число в третьей строке.
.jpg)
Получившийся квадрат является магическим, так как сумма 78 во всех линиях.
Умножение и деление с числом 7
Номер 1.
Рассмотри рисунки. Составь по каждому из них числовые выражения и найди их значения.

7 · 3 = 21 42 : 7 = 6
7 · 2 = 14 28 : 7 = 4
7 · 5 = 35 63 : 7 = 9
7 · 8 = 56 21 : 7 = 3
7 · 4 = 28 35 : 7 = 5
7 · 6 = 42 49 : 7 = 7
7 · 9 = 63 56 : 7 = 8
7 · 7 = 49 14 : 7 = 2
Повторим таблицу умножения.
Рассмотрим рисунки.
.jpg)
Выполним вычисления по рисункам.
7 · 3 = 21 42 : 7 = 6
7 · 2 = 14 28 : 7 = 4
7 · 5 = 35 63 : 7 = 9
7 · 8 = 56 21 : 7 = 3
7 · 4 = 28 35 : 7 = 5
7 · 6 = 42 49 : 7 = 7
7 · 9 = 63 56 : 7 = 8
7 · 7 = 49 14 : 7 = 2
Оформляем задание в тетрадь.
7 · 3 = 21 42 : 7 = 6
7 · 2 = 14 28 : 7 = 4
7 · 5 = 35 63 : 7 = 9
7 · 8 = 56 21 : 7 = 3
7 · 4 = 28 35 : 7 = 5
7 · 6 = 42 49 : 7 = 7
7 · 9 = 63 56 : 7 = 8
7 · 7 = 49 14 : 7 = 2
Номер 2.
7 · 8 63 : 7
7 · 7 56 : 8
4 · 6 : 8 (55 - 7) : 6
54 : 6 · 5 28 : (32 - 25)
7 ∙ 8 = 56 63 : 7 = 9
7 ∙ 7 = 49 56 : 8 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6, 7.
Рассуждаем и выполняем вычисления.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
63 : 7 = 9,
так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
56 : 8 = 7,
так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
1 2
4 · 6 : 8 = 3
1) 4 · 6 = 24
2) 24 : 8 = 3
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.
1 2
54 : 6 · 5 = 45
1) 54 : 6 = 9
2) 9 · 5 = 5 · 9 = 45
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.
1 2
(55 − 7) : 6 = 8
1) 55 – 7 = 55 – (5 + 2) = (55 – 5) – 2 = 50 – 2 = 48
2) 48 : 6 = 8
В данном выражении присутствуют действия вычитание и деление, а также скоби. Поэтому вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
2 1
28 : (32 – 25) = 4
1) 32 – 25 = 32 – (22 + 3) = (32 – 22) – 3 = 10 – 3 = 7
2) 28 : 7 = 4
В данном выражении присутствуют действия вычитание и деление, а также скоби. Поэтому вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
Оформляем задание в тетрадь.
7 ∙ 8 = 56
7 ∙ 7 = 49
63 : 7 = 9
56 : 8 = 7
4 ∙ 6 : 8 24 : 8 = 3
54 : 6 ∙ 5 = 9 · 5 = 45
(55 − 7) : 6 = 48 : 6 = 8
28 : (32 − 25) = 28 : 7 = 4
Номер 3.
На стоянке было 15 грузовых машин, легковых на 25 машин больше, чем грузовых, а мотоциклов в 5 раз меньше, чем легковых машин. Сколько мотоциклов было на стоянке?
Ответ:
1) 15 + 25 = 40 (шт.) – легковых было на стоянке.
2) 40 : 5 = 8 (шт.)
Ответ: 8 мотоциклов было на стоянке.
1) «на 25 машин больше», значит, вычисляется сложением.
2) «в 5 раз меньше», значит, вычисляется делением.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
На стоянке было 15 грузовых машин, а легковых – на 25 машин больше. Значит, что легковых машин было столько, сколько грузовых и еще 25 машин. Соответственно, чтобы узнать, сколько легковых машин было, нужно к количеству грузовых прибавить 25 машин.
1) 15 + 25 = 40 (шт.) – легковых машин было на стоянке.
Продолжаем рассуждение.
Мотоциклов было в 5 раз меньше, чем легковых машин. Значит, чтобы узнать, сколько мотоциклов было на стоянке, нужно количество легковых машин разделить на 5.
2) 40 : 5 = 8 (шт.) – было мотоциклов на стоянке.
Записываем ответ.
Ответ: 8 мотоциклов.
Решение выражением:
(15 + 25) : 5 = 8 (шт.)
Номер 4.
Рассмотри чертёж и начерти два отрезка так, чтобы длина одного была в 2 раза больше длины отрезка АВ, а длина другого – в 2 раза меньше длины отрезка CD.


Первый отрезок: 4 ∙ 2 = 8 (см)
Второй отрезок: 6 : 2 = 3 (см)
1) Отрезок - геометрическая фигура, часть прямой, ограниченная с двух сторон точками. Отрезок имеет длину, т.е. расстояние от точки до точки.
2) «в 2 раза больше», значит, вычисляется умножением.
3) «в 2 раза меньше», значит, вычисляется делением.
Измерим отрезки.
Измерим отрезки с помощью линейки.
-(2023).jpg)
АВ = 4 см
CD = 6 см
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
Длина отрезка АВ = 4 см, а отрезка которого нужно начертить – неизвестно, но он должен быть в 2 раза больше, чем отрезок АВ. В 2 раза больше, значит, 2 раза по длине отрезка АВ.
Соответственно, чтобы узнать, какова длина отрезка, нужно длину отрезка АВ умножить на 2. Назовем получившийся отрезок – отрезком КМ.
4 · 2 = 8 (см) – длина отрезка КМ.
Начертим отрезок КМ = 8 см с помощью линейки:
-(2023).jpg)
Продолжаем рассуждать.
Длина отрезка CD = 6 см, а отрезка которого нужно начертить – неизвестно, но он должен быть в 2 раза меньше, чем отрезок CD. В 2 раза меньше, значит половина от отрезка CD.
Соответственно, чтобы узнать, какова длина отрезка, нужно длину отрезка CD разделить на 2. Назовем получившийся отрезок – отрезком РТ.
6 : 2 = 3 (см) – длина отрезка РТ, так как 3 · 2 = 6.
Начертим отрезок РТ = 3 см с помощью линейки:
-(2023).jpg)
Оформляем задание в тетрадь.
Первый отрезок:
4 ∙ 2 = 8 (см) – длина отрезка, который в 2 раза больше АВ.
Второй отрезок:
6 : 2 = 3 (см) – длина отрезка, который в 2 раза меньше CD.
-(2023).jpg)
Ответ: 8 см и 3 см.
Номер 5.
В бензобаке машины было 8 л бензина. При заправке машины добавили 40 л бензина. За день израсходовали 25 л бензина.
Задай вопрос и реши задачу.
Было – 8 л
Добавили – 40 л
Израсходовали – 25 л
Осталось – ? л
Сколько литров бензина осталось в бензобаке?
1) 8 + 40 = 48 (л) – после добавки бензина.
2) 48 - 25 = 23 (л)
Ответ: 23 литра бензина осталось в бензобаке.
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Поставим вопрос к задаче.
Вопрос к задаче: Сколько литров бензина осталось в бензобаке?
Оформляем условие в виде краткой записи.
Было – 8 л
Добавили – 40 л
Израсходовали – 25 л
Осталось – ? л
Рассуждаем.
В бензобаке было 8 литров бензина. Добавили 40 литров. Добавили, то есть бензина в баке стало на 40 литров больше. Соответственно, чтобы узнать, сколько бензина стало, нужно к количеству бензина прибавить количество добавленного.
8 + 40 = 48 (л) – после добавки бензина.
Продолжаем рассуждение.
После покупки израсходовали 25 литров бензина. Израсходовали, значит, его стало меньше. Поэтому, чтобы узнать, сколько бензина осталось, нужно из общего количества бензина вычесть количество истраченного.
48 − 25 = 23 (л) − бензина осталось в бензобаке.
Записываем ответ.
Ответ: 23 литра бензина.
Решение выражением:
(8 + 40) – 25 = 23 (л)
Номер 6.
1) Сравни число клеток в фигурах.
2) Запиши номера симметричных фигур

1) Фигура 1: 6 ∙ 2 + 3 + 1 = 16 к.
Фигура 2: 8 ∙ 2 = 16 к.
Фигура 3: 6 ∙ 2 + 2 + 2 = 16 к.
В каждой фигуре по 16 клеток.
1) Симметричные фигуры: 2, 3.

Ось симметрии – линия, проведенная в фигуре, по которой можно сложить фигуру так, что равные части совпадут.
Рассмотрим фигуры.
Для удобства вычисления количества клеток в фигурах, разобьем фигуры на участки.
-(2023).jpg)
1 фигура состоит:
– из трёх строк по 3 клетки;
– из трёх строк по 2 клетки;
– одной клетки.
2 фигура состоит:
– из восьми строк по 2 клетки.
3 фигура состоит:
– из двух строк по 3 клетки;
– из двух строк по 2 клетки;
– из трёх строк по 3 клетки.
Вычислим.
Общее количество клеток складывается из количества клеток всех участков.
1 фигура:
3 · 3 + 3 · 2 + 1 = 9 + 6 + 1 = 16 (клеток)
2 фигура:
8 · 2 = 2 · 8 = 16 (клеток)
3 фигура:
2 · 3 + 2 · 2 + 2 · 3 = 6 + 4 + 6 = 16 (клеток)
Сравним количество клеток в фигурах:
16 кл. = 16 кл. = 16 кл.
Число клеток в фигурах одинаково.
Рассмотрим фигуры на симметрию.
Фигура 1 не имеет симметрию.
Фигура 2 имеет две оси симметрии – горизонтальную и вертикальную.
-(2023).jpg)
Фигура 3 имеет одну симметрию – горизонтальную.
-(2023).jpg)
Вывод: фигуры 2 и 3 имеют ось симметрии.
Номер 7.
6 · 2 + 6 · 4 ◯ 6 · 6
7 · 3 - 3 · 2 ◯ 3 · 4
35 : 5 + 10 : 5 ◯ 45 : 5
32 : 8 + 16 : 8 ◯ 40 : 8

Прежде, чем поставить знак больше, меньше, равно, нужно вычислить значение выражений в левой и правой части, а полученные значения сравнить.
Рассуждаем.
Сравним 6 · 2 + 6 · 4 и 6 · 6
Вычислим левую часть:
1 3 2
6 · 2 + 6 · 4 = 12 + 24 = 36
Выражение состоит из действий сложение и умножение, поэтому вначале выполняем умножение по порядку слева направо, а потом сложение.
Вычислим правую часть:
6 · 6 = 36
Сравним: 36 = 36
Значит, 6 · 2 + 6 · 4 = 6 · 6
Сравним 7 · 3 – 3 · 2 и 3 · 4
Вычислим левую часть:
1 3 2
7 · 3 – 3 · 2 = 21 – 6 = 15
Выражение состоит из действий вычитание и умножение, поэтому вначале выполняем умножение по порядку слева направо, а потом вычитание.
Вычислим правую часть:
3 · 4 = 12
Сравним: 15 > 12
Значит, 7 · 3 – 3 · 2 > 3 · 4
Сравним 35 : 5 + 10 : 5 и 45 : 5
Вычислим левую часть:
1 3 2
35 : 5 + 10 : 5 = 7 + 2 = 9
Вычислим правую часть:
45 : 5 = 9
Сравним: 9 = 9
Значит, 35 : 5 + 10 : 5 = 45 : 5
Сравним 32 : 8 + 16 : 8 и 40 : 8
Вычислим левую часть:
1 3 2
32 : 8 + 16 : 8 = 4 + 2 = 6
Вычислим правую часть:
40 : 8 = 5
Сравним: 6 > 5
Значит, 32 : 8 + 16 : 8 > 40 : 8
Запишем сравнение в тетрадь.
6 ∙ 2 + 6 ∙ 4 = 6 ∙ 6, так как 36 = 36
7 ∙ 3 − 3 ∙ 2 > 3 ∙ 4, так как 15 > 12
35 : 5 + 10 : 5 = 45 : 5, так как 9 = 9
32 : 8 + 16 : 8 > 40 : 8, так как 6 > 5
Номер 8.
Реши уравнения подбором
а · 10 = 90
12 : b = 2
x : 7 = 8
а ∙ 10 = 90
а = 90 : 10
а = 9
Проверка:
9 ∙ 10 = 90
90 = 90
Ответ: а = 9
12 : b = 2
b = 12 : 2
b = 6
Проверка:
12 : 6 = 2
2 = 2
Ответ: b = 6
х : 7 = 8
х = 8 ∙ 7
х = 56
Проверка:
56 : 7 = 8
8 = 8
Ответ: х = 56
1) Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия умножения и деления.
Рассуждаем.
а · 10 = 90
а – неизвестный множитель.
Подумай сколько раз нужно сложить число 10, чтобы получилось 90.
Число 10 нужно сложить 9 раз. Также сложение одинаковых слагаемых можно заменить умножением, поэтому число 10 нужно умножить на 9, чтобы получить 90.
а = 9
12 : b = 2
b – неизвестный делитель.
Вспомни таблицу умножения на 2. На какое число нужно умножить число 2, чтобы получить 12. Это число 6.
b = 6
х : 7 = 8
х – неизвестное делимое.
Вспомни таблицу умножения на 7. Какое число получится при умножении 7 на 8. Это число 56.
х = 56
Выполняем проверку.
а · 10 = 90
Проверка: вместо неизвестного а подставим число 9.
9 · 10 = 90
90 = 90 – верно.
12 : b = 2
Проверка: вместо неизвестного b поставим число 6.
12 : 6 = 2
2 = 2 – верно.
х : 7 = 8
Проверка: вместо неизвестного х подставим число 56.
56 : 7 = 8
8 = 8 – верно.
Оформляем задание в тетрадь.
а ∙ 10 = 90
а = 90 : 10
а = 9
Проверка:
9 ∙ 10 = 90
90 = 90
12 : b = 2
b = 12 : 2
b = 6
Проверка:
12 : 6 = 2
2 = 2
х : 7 = 8
х = 8 ∙ 7
х = 56
Проверка:
56 : 7 = 8
8 = 8
Задание внизу страницы.
9 ∙ 7 49 : 7
12 : 3 ∙ 5 (39 + 9) : 8
9 ∙ 7 = 63 49 : 7 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3, 4, 5, 6, 7.
Выполним умножение.
9 · 7 = 7 · 9 = 63
Применяем переместительное свойство умножения и таблицу умножения на 7.
Выполним деление.
49 : 7 = 7,
так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Расставим порядок действий и выполним вычисления.
1 2
12 : 3 · 5 = 20
1) 12 : 3 = 4
2) 4 · 5 = 20
1 2
(39 + 9) : 8 = 6
1) 39 + 9 = 39 + (8 + 1) = (39 + 1) + 8 = 40 + 8 = 48
2) 48 : 8 = 6
Оформим задание в тетрадь.
9 ∙ 7 = 63
49 : 7 = 7
12 : 3 ∙ 5 = 4 · 5 = 20
(39 + 9) : 8 = 48 : 8 = 6
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.