Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 24

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 24

Порядок выполнения действий

Номер 1.

Сравни выражения каждой пары: какие действия в них выполняются? В каком порядке выполняются эти действия и почему?

Ответ:

38 − 10 + 6 = 28 + 6 = 34 В первом примере сначала выполняют действие разность, а затем сложение, потому что при отсутствии скобок вычитание и сложение выполняются в том порядке, в котором они написаны: слева направо.
38 − (10 + 6) = 38 − 16 = 22 В этом примере сначала производится действие в скобках, а затем вычитание вне скобок.
24 : 3 ∙ 2 = 8 ∙ 2 = 16 В этом примере сначала производится действие деления, а затем умножения, потому что при отсутствии скобок умножение и деление выполняются в том порядке, в котором они написаны: слева направо.
24 : (3 ∙ 2) = 24 : 6 = 4 В этом примере сначала производится действие в скобках, а затем деление вне скобок.

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитание. Слева направо.

Шаг 1.
Рассмотрим примеры.

38 − 10 + 6 = 28 + 6 = 34
В данном примере присутствуют только действия сложение и вычитание – они равноправны. Поэтому действия выполняются по порядку слева направо: сначала - разность, а потом сложение.

38 − (10 + 6) = 38 − 16 = 22
В данном примере присутствуют действия сложение и вычитание, а также скобки. Действия в скобках выполняются первыми. Поэтому сначала производится сложение в скобках, а потом вычитание вне скобок.

24 : 3 ∙ 2 = 8 ∙ 2 = 16
В данном примере присутствуют только действия умножение и деление – они равноправны. Поэтому действия выполняются по порядку слева направо: сначала - деление, а потом умножение.

24 : (3 ∙ 2) = 24 : 6 = 4
В данном примере присутствуют действия умножение и деление, а также скобки. Действия в скобках выполняются первыми. Поэтому сначала производится умножение в скобках, а потом деление вне скобок.

Шаг 2.
Расставим действия.

1 2
38 − 10 + 6

2 1
38 − (10 + 6)

1 2
24 : 3 ∙ 2

2 1
24 : (3 ∙ 2)

Номер 2.

Объясни, как надо выполнять действия.

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 24 номер 2

Так как в примере есть скобки, то сначала производится действие в них. Затем по правилу идет действие умножения, а потом сложения.

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 24 номер 2-1

Так как в примере скобок нет, то действия производятся в таком порядке: сначала деление и умножение по порядку (слева направо), затем вычитание и сложение по порядку (слева направо).

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.

Шаг 1.
Рассмотрим примеры.

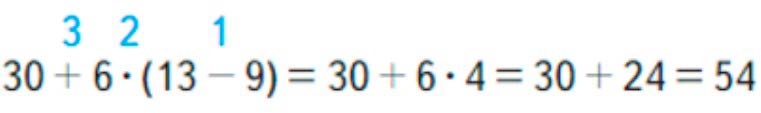
В данном примере есть действия умножение, сложение и вычитание, а также скобки. Поэтому сначала выполняем действие, записанное в скобках – вычитание, потом выполняем умножение и последним действие – сложение.

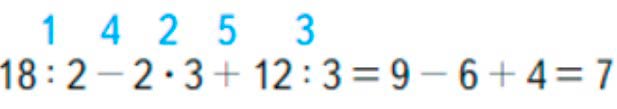
В данном примере есть действия умножение, деление, сложение и вычитание. Скобок в примере нет. Вначале выполняем действия умножение и деление по порядку слева направо, а лишь потом сложение и вычитание по порядку слева направо.

Шаг 2.
Выполним вычитания по действиям.

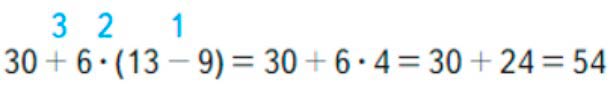
1) 13 – 9 = 4
2) 6 · 4 = 24
3) 30 + 24 = 54

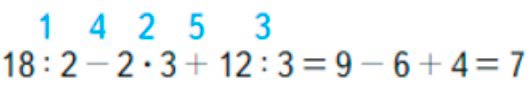
1) 18 : 2 = 9
2) 2 · 3 = 6
3) 12 : 3 = 4
4) 9 – 6 = 3
5) 3 + 4 = 7

Номер 1.

Вычисли

1) 30 + 15 - 6
60 - 7 + 18
18 : 3 + 4 · 3
2 · 8 + 21 : 7
12 + 6 : 2 - 7 · 2
37 + 9 - 6 : 2 · 3

2) 70 : (3 + 7) + 24
60 : 6 · 3 - 18
100 - (24 - 18) · 3
100 - (72 - 67) · 2

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 24, номер 1

Подсказка:

Вспомним таблицу умножения, а также порядок действий.

Шаг 1.
Выполняем вычисления.

30 + 15 − 6 = 39
1) 30 + 15 = 45
2) 45 − 6 = 39

60 − 7 + 18 = 71
1) 60 − 7 = 53
2) 53 + 18 = 71

18 : 3 + 4 · 3 = 18
1) 18 : 3 = 6
2) 4 · 3 = 12
3) 6 + 12 = 18

2 · 8 + 21 : 7 = 19
1) 2 · 8 = 16
2) 21 : 7 = 3
3) 16 + 3 = 19

12 + 6 : 2 − 7 · 2 = 1
1) 6 : 2 = 3
2) 7 · 2 = 14
3) 12 + 3 = 15
4) 15 − 14 = 1

37 + 9 − 6 : 2 · 3 = 37
1) 6 : 2 = 3
2) 3 · 3 = 9
3) 37 + 9 = 46
4) 46 − 9 = 37

70 : (3 + 7) + 24 = 31
1) 3 + 7 = 10
2) 70 : 10 = 7
3) 7 + 24 = 31

60 : 6 · 3 − 18 = 12
1) 60 : 6 = 10
2) 10 · 3 = 30
3) 30 − 18 = 12

100 − (24 − 18) · 3 = 82
1) 24 − 18 = 6
2) 6 · 3 = 18
3) 100 − 18 = 82

100 − (72 − 67) · 2 = 90
1) 72 − 67 = 5
2) 5 · 2 = 10
3) 100 − 10 = 90

Шаг 2.
Оформляем задание в тетрадь.

Номер 2.

Ответ:

Подсказка:

Если произведение двух множителей разделить на один из них, получится другой множитель.

Шаг 1.
Выполняем вычисления.

8 · 3 = 24
21 : 7 = 3
8 : 4 = 2
15 : 5 = 3
6 · 3 = 18
18 : 2 = 9

Шаг 2.
Оформляем задание в тетрадь.

Номер 3.

Упаковщица уложила в коробку 2 ряда жёлтых кубиков, по 8 кубиков в ряду, и 16 красных кубиков. Сколько всего кубиков было в коробке?

Ответ:

Жёлтые – 2 р. по 8 к.
Красные – 16 к.
Всего – ? к.

1) 2 ∙ 8 = 16 (к.) – желтых.
2) 16 + 16 = 32 (к.)
Ответ: 32 кубика всего в коробке.

Подсказка:

Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.

Шаг 1.
Оформляем задание в виде краткой записи.

Жёлтые – 2 р. по 8 к.
Красные – 16 к.
Всего – ? к.

Шаг 2.
Рассуждаем.

Узнаем, сколько продавец положила в коробку желтых кубиков, для этого количество рядов с желтыми кубиками умножим на количество кубиков в ряду.

1) 2 · 8 = 16 (к.) – желтых.

Шаг 3.
Продолжаем рассуждение.

Узнаем, сколько красных и желтых кубиков в коробке, для этого сложим количество тех и других вместе.

2) 16 + 16 = 32 (к.)

Шаг 4.
Записываем ответ.

Ответ: 32 кубика всего в коробке.

Номер 4.

В трёх одинаковых рядах 24 стула. Сколько стульев в каждом ряду? Сколько стульев в двух таких рядах? в десяти рядах?

Ответ:

3 р. – 24 ст.
1 р. – ? ст.
2 р. – ? ст.
10р. – ? ст.

1) 24 : 3 = 8 (ст.) – в одном ряду.
2) 8 · 2 = 16 (ст.) – в двух рядах.
3) 8 · 10 = 80 (ст.) – в 10 рядах
Ответ: в одном ряду 8 стульев; в двух рядах 16 стульев; в 10 рядах 80 стульев.

Подсказка:

Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.

Шаг 1.
Оформляем задание в виде краткой записи.

3 р. – 24 ст.
1 р. – ? ст.
2 р. – ? ст.
10р. – ? ст.

Шаг 2.
Рассуждаем.

Узнаем, сколько стульев в одном ряду, для этого количество стульев в трех рядах разделим на 3.

1) 24 : 3 = 8 (ст.) – в одном ряду.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько стульев в двух рядах, нужно количество стульев в одном ряду умножить на 2.

2) 8 · 2 = 16 (ст.) – в двух рядах.

Шаг 4.
Продолжаем рассуждение.

Чтобы узнать, сколько стульев в десяти рядах, нужно количество стульев в одном ряду умножить на 10.

3) 8 · 10 = 80 (ст.) – в 10 рядах.

Шаг 5.
Записываем ответ.

Ответ: в одном ряду 8 стульев; в двух рядах 16 стульев; в 10 рядах 80 стульев.

Номер 5.

Высота берёзы 15 м, а рябины 3 м. На сколько метров берёза выше рябины? Во сколько раз берёза выше рябины?

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 24, номер 5

1) 15 - 3 = 12 (м.) – береза выше рябины.
2) 15 : 3 = 5 (р.) – береза выше рябины.
Ответ: на 12 метров берёза выше рябины; в 5 раз берёза выше рябины.

Подсказка:

Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.

Шаг 1.
Оформляем задание в виде краткой записи.

Шаг 2.
Рассуждаем.

Чтобы узнать, на сколько береза выше рябины, нужно из высоты березы вычесть высоту рябины.

1) 15 − 3 = 12 (м.) – береза выше рябины.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, во сколько раз береза выше рябины, нужно высоту березы разделить на высоту рябины.

2) 15 : 3 = 5 (р.) – береза выше рябины.

Шаг 4.
Записываем ответ.

Ответ: на 12 метров выше; в 5 раз выше.

Номер 6.

1) Найди периметр каждого многоугольника.
2) Сколько осей симметрии у каждой фигуры?

Ответ:

1) Периметр синего квадрата:
25 + 25 + 25 + 25 = 100 (мм)
100 мм = 10 см
Ответ: периметр ABCD равен 10 см.

Периметр красного треугольника:
3 + 3 + 3 = 3 ∙ 3 = 9 (см)
Ответ: периметр KLM равен 9 см.

Периметр зелёного прямоугольника:
(3 + 3) + (2 + 2) = 6 + 4 = 10 (см)
Ответ: периметр NOPT равен 10 см.

2) В квадрате 4 оси симметрии.
В треугольнике 3 оси симметрии.
В прямоугольнике 2 оси симметрии.

Подсказка:

Ось симметрии – это прямая или воображаемая линия, которая делит геометрическую фигуру на две зеркально одинаковых фигуры.

Шаг 1.
Рассмотрим фигуры.

Измерим длины сторон каждой из фигур.

Шаг 2.
Вычислим периметр каждой фигуры.

Периметр синего квадрата:
25 + 25 + 25 + 25 = 100 (мм)
100 мм = 10 см
Ответ: периметр ABCD равен 10 см.

Периметр красного треугольника:
3 + 3 + 3 = 3 ∙ 3 = 9 (см)
Ответ: периметр KLM равен 9 см.

Периметр зелёного прямоугольника:
(3 + 3) + (2 + 2) = 6 + 4 = 10 (см)
Ответ: периметр NOPT равен 10 см.

Шаг 3.
Сосчитаем оси симметрии каждой фигуры.

В квадрате 4 оси симметрии.
В треугольнике 3 оси симметрии.
В прямоугольнике 2 оси симметрии.

Номер 7.

В двух вазах было 13 яблок. Когда из одной вазы взяли 2 яблока, а в другую добавили 3 яблока, яблок в вазах стало поровну. Сколько яблок было в каждой вазе сначала?

Ответ:

1) 13 - 2 + 3 = 14 (ябл.) – стало в двух вазах.
2) 14 : 2 = 7 (ябл.) – стало в одной вазе.
3) 7 + 2 = 9 (ябл.) – было в одной вазе.
4) 7 - 3 = 4 (ябл.) – было во второй вазе.
Ответ: в первой вазе было 9 яблок, во второй 4 яблока.

Подсказка:

Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.

Шаг 1.
Оформляем задание в виде краткой записи.

Шаг 2.
Рассуждаем.

Чтобы узнать, сколько яблок стало в двух вазах, нужно из 13 яблок, которые были изначально, вычесть 2 яблока, которые взяли из первой вазы. Затем к полученному количеству прибавить 3 яблока, которые были добавлены во вторую вазу.

1) 13 − 2 + 3 = 14 (яб.) – стало в двух вазах.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько яблок стало в одной вазе, нужно количество яблок в двух вазах разделить на 2.

2) 14 : 2 = 7 (яб.) – стало в одной вазе.

Шаг 4.
Продолжаем рассуждение.

Чтобы узнать, сколько яблок было в первой вазе, нужно к количеству яблок в одной вазе (стало) прибавить 2.

3) 7 + 2 = 9 (яб.) – было в первой вазе.

Шаг 5.
Продолжаем рассуждение.

Чтобы узнать, сколько яблок было во второй вазе, нужно из количества яблок в одной вазе (стало) вычесть 3.

4) 7 − 3 = 4 (яб.) – было во второй вазе.

Шаг 6.
Записываем ответ.

Ответ: в первой вазе было 9 яблок, во второй 4 яблока.

Задание внизу страницы

72 - (47 - 20) : 3 = ⬜
21 : (15 - 8) · 9 = ⬜

Ответ: