Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 23

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
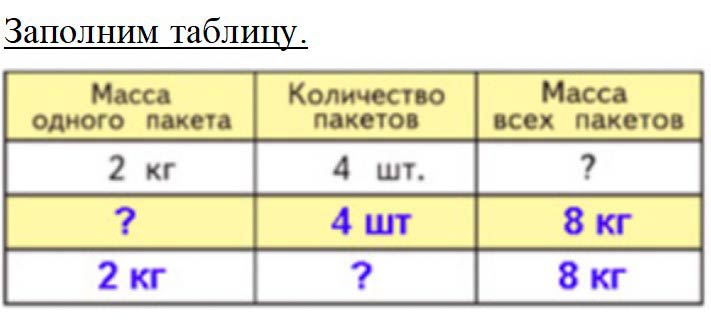
Запиши задачи кратко в таблицу и реши их.
1) Масса пакета с мукой 2 кг. Узнай массу 4 таких пакетов.
2) Масса 4 одинаковых пакетов с мукой 8 кг. Узнай массу одного пакета.
3) Масса одного пакета с мукой 2 кг. Сколько пакетов потребуется, чтобы разложить в них поровну 8 кг муки?
Задача 1:
2 ∙ 4 = 8 (кг) – масса всех пакетов.
Ответ: масса четырёх пакетов восставляет 8 кг.
Задача 2:
8 : 4 = 2 (кг) – масса одного пакета.
Ответ: масса одного пакета составляет 2 кг.
Задача 3:
8 : 2 = 4 (пак.) – потребуется.
Ответ: 4 пакета потребуется, чтобы разложить 8 кг муки.

Данная задача характеризуется зависимостями между элементами:
Масса 1 пакета · количество пакетов = общая масса.
Общая масса : масса 1 пакета = количество пакетов.
Общая масса : количество пакетов = масса 1 пакета.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, какова общая масса всех пакетов с мукой, нужно массу 1 пакета умножить на количество пакетов.
2 · 4 = 8 (кг) – масса 4 пакетов.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, какова масса одного пакета, нужно общую массу пакетов разделить на количество пакетов.
8 : 4 = 2 (кг) – масса одного пакета.
Записываем ответ.
Ответ: 2 кг.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать количество пакетов, нужно общую массу муки всех пакетов разделить на массу 1 пакета.
8 : 2 = 4 (шт.) – количество пакетов.
Записываем ответ.
Ответ: 4 пакета.
Номер 2.
Составь свою задачу на нахождение массы нескольких одинаковых посылок, если известны масса одной посылки и количество таких посылок, и реши ее.
Ответ:
Школьники отправили в детский сад 4 посылки с игрушками. Масса одной посылки 5 кг. Сколько кг игрушек отправили школьники? 5 ∙ 4 = 20 (кг) Ответ: 20 кг игрушек отправили школьники.
Данная задача характеризуется зависимостями между элементами:
Масса 1 посылки · количество посылок = общая масса.
Общая масса : масса 1 посылки = количество посылок.
Общая масса : количество посылок = масса 1 посылки.
Составим задачу.
Школьники отправили в детский сад 20 кг игрушек в посылках. Масс одной посылки 5 кг. Сколько посылок отправили школьники?
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, общую массу посылок, массу одной посылки умножить на количество посылок.
7 · 5 = 35 (кг) – общая масса посылок
Записываем ответ.
Ответ: 35 кг.
Номер 3.
Рассмотри ряд чисел и запиши пропущенные числа.
Ответ:1) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. 2) 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
1) Прежде, чем дополнить ряд чисел, необходимо выявить закономерность, т.е. правило, как он составлен.
2) Для этого рассмотри числа с разных сторон: сколько в нем знаков, на что они делятся, из каких цифр составлены.
Рассмотрим первый ряд чисел.
Числа идут по возрастанию через одно число, значит это числа, которые без остатка делятся на 2, т.е. четные.
Рассмотрим второй ряд чисел.
Числа идут по возрастанию через два числа, значит это числа, которые делятся без остатка на 3, т.е. являются результатами таблицы умножения на три.
Дополним ряды.
1) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
2) 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
Номер 4.
К произведению чисел 5 и 3 прибавь число 35.
Ответ:1-й способ решения:

2-й способ решения: 5 ∙ 3 + 35 = 15 + 35 = 50.
Вычисление значений выражения сводится к применению правила:
а + (в + с) = (а + в) + с – прибавления суммы к числу:
Составим выражение.
Произведение чисел 5 и 3 – это значит, что число 5 нужно умножить на 3.
5 · 3 – произведение.
Теперь к данному произведению нужно прибавить число 35, значит получим выражение:
5 · 3 + 35.
Найдём значение выражения.
5 · 3 + 35 = 15 + 35 = 15 + (30 + 5) = (15 + 5) + 30 = 20 + 30 = 50
Вначале число 5 умножили на 3, а потом к полученному произведению прибавили 35 по правилу прибавление суммы к числу.
Номер 5.
Для ремонта дома сначала привезли 18 бревен, а потом еще 15. Осталось привезти 9 бревен. Поставь вопрос и реши задачу.
Ответ:
Сколько бревен потребовалось для ремонта дома?
1-й способ решения:
1) 18 + 15 = 33 (бр.) – привезли.
2) 33 + 9 = 42 (бр.)
Ответ: 42 бревна всего потребовалось.
2-й способ решения: 18 + 15 + 9 = 42 (б.) – нужно всего. Ответ: 42 бревна.
Вопрос задачи: Сколько бревен потребовалось для ремонта дома?
Оформляем условие в виде краткой записи.

Рассуждаем.
Узнаем количество привезенных брёвен. Общее количество бревен, которые привезли сначала, складывается из количества бревен первой и второй группы. Значит, чтобы узнать, сколько бревен привезли сначала, нужно сложить две группы бревен.
18 + 15 = 33 (бр.) – привезли всего
Продолжаем рассуждения.
Узнаем общее количество брёвен.
Общее количество бревен, которые привезли, складывается из количества бревен, которые привезли сначала, и которые привезли потом. Значит, чтобы узнать, сколько бревен привезли всего, нужно сложить бревна, которые привезли сначала и которые привезли потом.
33 + 9 = 42 (бр.) – нужно для ремонта дома.
Записываем ответ.
Ответ: 42 бревна.
Решение с помощью выражения:
(18 + 15) + 9 = 42 (бр.)
Номер 6.
Ответ:
Вычисление значений выражения сводится к применению правил:
(а + в) + с = (а + с) + в – прибавление числа к сумме;
а – (в + с) = (а – в) – с – вычитание суммы из числа;
(а + в) – с = (а – с) + в – вычитание числа из суммы.
Выполним устные рассуждения.
26 + 17 + 3 = 26 + (17 + 3) = 26 + 20 = 40 + 6 = 46
Сначала складываем числа 17 и 3, а потом к полученной сумме прибавляем число 26.
Применяем правило прибавление числа к сумме.
45 – 20 – 9 = (45 – 20) – 9 = 25 – 9 = 25 – (5 + 4) = (25 – 5) – 4 = 20 – 4 = 16
Вначале из числа 45 вычтем число 20, а потом из полученной разноси вычтем число 9.
Чтобы из числа 25 вычесть число 9, разложим число 9 на сумму чисел 5 и 4, из числа 25 вначале вычтем число 5, а потом вычтем число 4.
Применяем правило вычитание суммы из числа.
65 – 60 + 95 = (65 + 95) – 60 = 160 – 60 = 100
Сначала складываем числа 65 и 95, а потом из полученной суммы вычитаем число 60.
Применяем правило вычитание суммы из числа.
37 + 8 + 22 = 37 + (8 + 22) = 37 + 30 = 60
Сначала складываем числа 8 и 22, а потом к полученной сумме прибавляем число 37.
Применяем правило прибавление числа к сумме.
1 · 7 · 10 – 25 = 70 – 25 = (70 – 20) – 5 = 50 – 5 = 45
Чтобы из числа 70 вычесть число 25, разложим число 25 на сумму чисел 20 и 5, потом из числа 70 сначала вычтем число 20, а потом число 5.
Применяем правило вычитание суммы из числа.
0 · 3 · 10 + 40 = 0 + 40 = 40
При умножении любого числа на ноль получается ноль.
Оформляем задание в тетрадь.
26 + 17 + 3 = 26 + (17 + 3) = 46
45 − 20 − 9 = 25 – 9 = 16
65 − 60 + 95 = 5 + 95 = 100
37 + 8 + 22 = 37 + (8 + 22) = 67
1 ∙ 7 ∙ 10 − 25 = 70 – 25 = 45
0 ∙ 3 ∙ 10 + 40 = 0 + 40 = 40
Номер 7.
Расставь знаки «+» и «–» так, чтобы равенства стали верными.
Ответ:32 − 9 + 7 = 30 18 + 6 − 5 = 19 50 + 5 − 8 = 47 70 − 8 + 6 = 68
1) Выполняй разные действия с числами, перебирай знаки арифметических действий. Пробуй, пока не придешь к верному решению.
2) Вычисление значений выражения сводится к применению правил:
(а + в) + с = (а + с) + в – прибавление числа к сумме;
а – (в + с) = (а – в) – с – вычитание суммы из числа;
(а + в) – с = (а – с) + в – вычитание числа из суммы.
Расставим знаки в выражениях.
32 − 9 + 7 = 30
50 + 5 − 8 = 47
18 + 6 − 5 = 19
70 − 8 + 6 = 68
Проверим вычисления.
32 – 9 + 7 = (32 + 7) – 9 = 39 – 9 = 30
Вначале к числу 32 прибавим число 9, а потом из суммы вычтем число 9.
Применяем правило вычитание числа из суммы.
50 + 5 – 8 = (50 + 5) – 8 = 55 – 8 = 55 – (5 + 3) = (55 – 5) – 3 = 50 – 3 = 47
Вначале к числу 50 прибавим число 5, а потом из полученной суммы вычтем число 8, разложив его на сумму чисел 5 и 3.
Применяем правило вычитание суммы из числа.
18 + 6 – 5 = 18 + (6 – 5) = 18 + 1 = 19
Вначале из числа 6 вычтем число 5, а потом к числу 18 прибавим полученную разность.
Используем правило прибавление числа к сумме.
70 – 8 + 6 = (70 – 8) + 6 = 62 + 6 = 68
Вначале из числа 70 вычтем число 8, а потом к полученной разности прибавим число 6.
Используем правило прибавление числа к сумме.
Оформляем задание в тетрадь.
Номер 8.
Есть ли ось симметрии у отрезка? Начерти любой отрезок. Дай ответ.
Ответ:
Ось симметрии есть, всегда можно провести линию, которая разделит отрезок на две равные половины.

1) Вспомни, что отрезок – геометрическая фигура, представляющая собой часть прямой, ограниченную с двух сторон точками.
2) Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
Рассуждаем.
Отрезок имеет длину, то есть расстояние между точками можно измерить. Поэтому и середину отрезка можно найти, разделив отрезок пополам, а через середину – провести ось симметрии.
Начертим отрезок.
Например, начертим отрезок длинной 5 см = 50 мм – это 10 клеток.
Найдём середину отрезка, поделив длину отрезка пополам.
10 клеток : 2 = 5 клеток = 2 см 5 мм = 25 мм – середина отрезка.
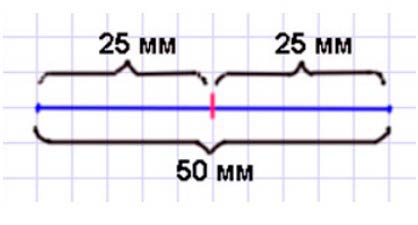
Середина отрезка – это и есть ось симметрии. На рисунке она показана красным цветом.
Задание внизу страницы
Разность чисел 100 и 75 уменьши на 12.
Ответ:
1-й способ решения:

2-й способ решения: (100 – 75) – 12 = 13 1) 100 – 75 = 25 2) 25 – 12 = 13
Вычисление значений выражения сводится к применению правила:
а – (в + с) = (а – в) – с – вычитания суммы из числа.
Составим выражение.
Разность чисел 100 и 75, это значит сто из числа 100 нужно выесть число 75.
100 – 75 – разность.
Теперь эту разность нужно уменьшить на 12, то есть вычесть 12.
И получим выражение: 100 – 75 – 12.
Вычислим выражение.
(100 – 75) – 12 = 25 – 12 = 25 – (5 + 7) = (25 – 5) – 7 = 20 – 7 = 13
Вначале из числа 100 вычтем число 75, а после из получившейся разности вычтем число 12, представив его в виде суммы чисел 5 и 7.
Используем правило вычитание суммы из числа.
Задание на полях страницы
Ребусы:

Ответ:

1) Помни, единицы можно складывать и вычитать только с единицами, десятки – с десятками.
2) Помни, что 1 дес. = 10 ед.
Рассуждаем.
Количество единиц уменьшаемого не известно, но известно количество единиц уменьшаемого и единицы разности.
Чтобы найти неизвестную цифру, нужно сложить количество единиц вычитаемого и единицы разности.
9 ед. + 5 ед. = 14 ед.= 1 дес. 4 ед. – в уменьшаемом 4 единицы.
Вместо первой звёздочки – цифра 4.
Продолжаем рассуждения.
Количество десятков вычитаемого не известно, но известно количество десятков уменьшаемого и количество десятков разности.
Чтобы найти неизвестную цифру, нужно из количества десятков уменьшаемого вычесть количество десятков разности.
7 дес. – 5 дес. = 2 дес. и ещё 1 дес. занимали для вычисления единиц, поэтому 2 дес. – 1 дес. = 1 дес. – в вычитаемом 1 десяток.
Вместо второй звездочки – цифра 1.
Записываем ответ.
Получим равенство:
74 – 15 = 59.
Запишем равенство в столбик:
.jpg)
Рассуждаем.
Количество единиц второго слагаемого неизвестно, но известно количество единиц первого слагаемого и количество единиц суммы.
Нужно подумать при сложении с какой цифрой 9 ед. станут 3 ед.
Это цифра 4, так как 9 ед. + 4 ед. = 13 ед. – это 1 дес. и 3 ед.
Во втором слагаемом 4 единицы.
Вместо первой звездочки – цифра 4.
Продолжаем рассуждения.
2) Количество десятков первого слагаемого неизвестно. Но известно количество десятков второго слагаемого и количество десятков суммы.
Чтобы найти неизвестную цифру, нужно из количества десятков суммы вычесть количество десятков второго слагаемого.
6 дес. – 2 дес. = 4 дес. и ещё занимали 1 дес. для вычисления единиц, потому 4 дес. – 1 дес. = 3 дес. – в первом слагаемом.
Вместо второй звездочки – цифра 3.
Записываем ответ.
Получаем выражение:
39 + 24 = 63
Запишем равенство в столбик:
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.