Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 109
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Изображение математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 109")
Странички для любознательных
Готовимся к олимпиаде
Номер 1.
Какие числа пропущены?
Ответ:20 + 11 + 69 = 100 (6 + 92) : 1 = 98 70 ‒ 35 ‒ 10 = 25 (36 + 14) ∙ 0 = 0 7 ∙ 2 ∙ 2 : 4 = 7 8 ∙ 6 : 48 = 1
Попытайся превратить равенства в уравнения, подставив вместо окошка, х. Реши уравнения.
Рассуждаем.
20 + х + 69 = 100
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
70 − 35 − х = 25
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
7 ∙ х ∙ 2 : 4 = 7
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
(х + 92) : 1 = 98
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
(36 + 14) ∙ х = 0
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
8 ∙ 6 : х = 1
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение разности.
Решим уравнения.
20 + х + 69 = 100
Для упрощения уравнения сложим числа 10 и 69.
89 + х = 100
х = 100 - 89
11 – пропущенное число.
70 − 35 − х = 25
Для упрощения уравнения из числа 70 вычтем число 35.
35 – х = 25
х = 35 - 25
10 – пропущенное число.
7 ∙ х ∙ 2 : 4 = 7
Для упрощения уравнения число 7 умножим на число 2.
14 · х : 4 = 7
Чтобы узнать значение произведения 14 · х нужно число 7 умножить на 4.
х ∙ 14 = 7 · 4
х · 14 = 28
х = 28 : 14
2 – пропущенное число.
(х + 92) : 1 = 98
Чтобы узнать значение суммы х + 92 нужно 98 умножить на 1.
х + 92 = 98 ∙ 1
х + 92 = 98
х = 98 − 92
х = 6
6 – пропущенное число.
(36 + 14) ∙ х = 0
Упростим уравнение вычислив значение в скобках.
50 ∙ х = 0
х = 0 : 50
х = 0
0 – пропущенное число.
8 ∙ 6 : х = 1
Упростим уравнение умножим числа 8 и 6.
48 : х = 1
х = 48 : 1
х = 48
48 – пропущенное число.
Сделаем проверку.
20 + х + 69 = 100
Проверка: вместо неизвестного подставим число 11.
20 + 11 + 69 = 20 + (11 + 69) = 20 + 80 = 100
100 = 100 – верно.
70 − 35 − х = 25
Проверка: вместо неизвестного подставим число 10
70 – 35 – 10 = 35 – 10 = 25
25 = 25 – верно.
7 ∙ х ∙ 2 : 4 = 7
Проверка: вместо неизвестного подставим число 2
7 · 2 · 2 : 4 = 14 · 2 : 4 = 28 : 4 = 7
7 = 7 – верно.
(х + 92) : 1 = 98
Проверка: вместо неизвестного подставим число 6
(6 + 92) : 1 = 98 : 1 = 98
98 = 98 – верно.
(36 + 14) ∙ х = 0
Проверка: вместо неизвестного подставим число 0
(36 + 14) · 0 = 50 · 0 = 0
0 = 0 – верно.
8 ∙ 6 : х = 1
Проверка: вместо неизвестного подставим число 48
8 · 6 : 48 = 48 : 48 = 1
1 = 1 – верно.
Оформляем задание в тетрадь.
20 + 11 + 69 = 100
70 – 35 – 10 = 25
7 · 2 · 2 : 4 = 7
(6 + 92) : 1 = 98
(36 + 14) · 0 = 0
8 · 6 : 48 = 1
Номер 2.
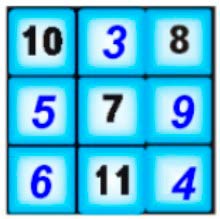
В свободных клетках квадрата 1 размести еще числа 3, 4, 5, 6, 9 так, чтобы получить магический квадрат.
Проверка:
10 + 5 + 6 = 10 + 11 = 21
3 + 7 + 11 = 10 + 11 = 21
8 + 9 + 4 = 8 + 13 = 21
10 + 3 + 8 = 10 + 11 = 21
5 + 7 + 9 = 12 + 9 = 21
6 + 11 + 4 = 10 + 11 = 21
10 + 7 + 4 = 10 + 11 = 21
6 + 7 + 8 = 13 + 8 = 21
Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Пояснение:
Рассмотрим первый магический квадрат.
Сумма в данном магическом квадрате будет равна 21.
Рассмотрим первую строчку.
10 + + 8 = 21
В строчке не хватает второго числа.
Упростим выражение сложив числа 10 и 8.
18 + = 21
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
21 – 18 = 3
3 – недостающее число в первой строке.
Рассмотрим диагональ.
10 + 7 + = 21
В строчке не хватает третьего числа.
Упростим выражение сложив числа 10 и 7.
17 + = 21
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
21 – 17 = 4
4 – недостающее число в диагонали.
Рассмотрим третий столбец.
В столбце не хватает второго числа.
8 + + 4 = 21
Упростим выражение сложив числа 8 и 4.
12 + = 21
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
21 – 12 = 9
9 – недостающее число в третьем столбце строке.
Рассмотрим вторую строку.
В строчке не хватает первого числа.
+ 7 + 9 = 21
Упростим выражение сложив числа 7 и 9.
+ 16 = 21
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
21 – 16 = 5
5 – недостающее число во второй строке.
Рассмотрим третью строчку.
В строчке не хватает первого числа.
+ 11 + 4 = 21
Упростим выражение сложив числа 11 и 4.
+ 15 = 21
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
21 – 15 = 6
6 – недостающее число в третьей строке.
Делаем вывод.
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 21.
Номер 3.
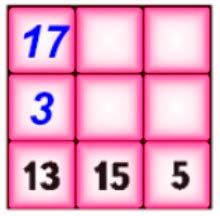
Оставляя на местах числа 13, 15 и 5 в квадрате 2, расставь в его пустые клетки числа 3, 7, 9, 11, 17, 19 так, чтобы получить магический квадрат.
Проверка:
13 + 15 + 5 = 13 + 20 = 33
3 + 11 + 19 = 3 + 30 = 33
17 + 7 + 9 = 17 + 16 = 33
17 + 3 + 13 = 20 + 13 = 33
7 + 11 + 15 = 18 + 15 = 33
9 + 19 + 5 = 14 + 19 = 33
17 + 11 + 5 = 17 + 16 = 33
13 + 11 + 9 = 13 + 20 = 33
Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Найдём магическую сумму.
13 + 15 + 5 = 13 + (15 + 5) = 13 + 20 = 33 – магическая сумма.
Рассмотрим первый столбец.
+ + 13 = 33
В столбце не хватает первого и второго чисел.
Упростим выражение из числа 33 вычтем число 13.
+ = 20
Из чисел 3, 7, 9, 11, 17, 19 нужно составить сумму 20.
20 = 3 + 17
Числа 3 и 17 – недостающие числа в первом столбце.
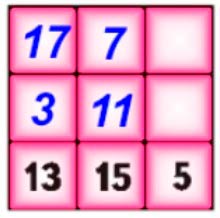
Рассмотрим второй столбец.
+ + 15 = 33
В столбце не хватает первого и второго чисел.
Упростим выражение из числа 33 вычтем число 15.
+ = 18
Из чисел 7, 9, 11, 19 нужно составить сумму 18.
18 = 7 + 11
Числа 7 и 11 – недостающие числа во втором столбце.
Рассмотрим третий столбец.
+ + 5 = 33
В столбце не хватает первого и второго чисел.
Упростим выражение из числа 33 вычтем число 5.
+ = 28
28 = 9 + 19
Числа 9 и 19 – недостающие числа в третьем столбце.
Делаем вывод.
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 33.
Номер 4.
Используя знаки действий и, если надо, скобки, запиши число 10 четырьмя тройками.
Ответ:3 ∙ 3 + 3 : 3 = 10
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Запишем выражения.
Есть несколько вариантов, как можно из четырёх троек получить число 10.
1) 3 ∙ 3 + 3 : 3 = 9 + 1 = 10
2) 3 : 3 + 3 ∙ 3 = 1 + 9 = 10
3) (33 – 3) : 3 = 30 : 3 = 10
Выполним проверку по действиям.
1 3 2
3 · 3 + 3 : 3 = 10
1) 3 · 3 = 9
2) 3 : 3 = 1
3) 9 + 1 = 10
1 3 2
3 : 3 + 3 · 3 = 10
1) 3 : 3 = 1
2) 3 · 3 = 9
3) 1 + 9 = 10
1 2
(33 − 3) : 3 = 10
1) 33 – 3 = 30
2) 30 : 3 = 10, так как 3 · 10 = 30
Номер 5.
Два одинаковых пакета молока и пачка творога стоят 94 р. Две такие же пачки творога и один такой же пакет молока стоят 80 р. На сколько рублей один пакет молока дороже одной пачки творога?
Запиши только ответ.
Ответ: на 14 рублей 1 пачка молока дороже, чем 1 пачка творога.
Попытайся ставить схематический рисунок для решения задачи. По данной модели составить решение будет намного проще.
Оформляем условие в виде рисунка.
По условию два одинаковых пакета молока и пачка творога стоят 94 рубля, а две такие же пачки творога и один такой же пакет молока стоят 80 рублей. Оформим условие задачи.
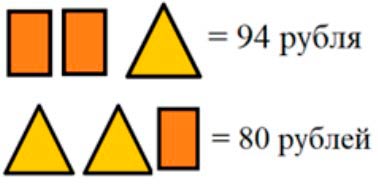
Рассуждаем.
В обоих товарах есть одинаковые товары, вычеркнем их.
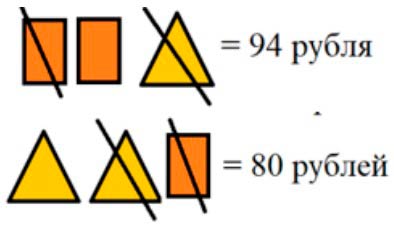
В первом наборе остался пакет молока, а во втором - пачка творога.
При этом, стоимость первой покупки – 94 рубля, а второй – 80 рублей.
Чтобы узнать, на сколько стоимость одной покупки больше стоимости другой, нужно из большей стоимости вычесть меньшую стоимость покупкми.
94 – 80 = 14 (р.) – разницам между покупками.
Значит, разница между пакетом молока и пачкой творога равна 14 рублей.
Получается, что стоимость пакета молока больше стоимости пачки творога на 14 рублей.
Записываем ответ.
Ответ: на 14 рублей 1 пачка молока дороже, чем 1 пачка творога.
Номер 6.
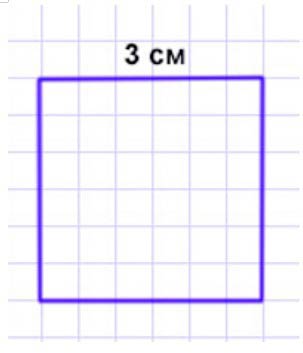
Начерти прямоугольник с периметром 12 см и с наибольшей площадью.
Ответ:Начертим квадрат, он является прямоугольником с равными сторонами.
Р = (а + b) · 2
Р = 12 см, значит, нужно определить такие прямоугольники, периметр которых равен 12.
Это прямоугольники со сторонами:
1 см и 5 см, потому что (1 + 5) · 2 = 6 · 2 = 12 см
2 см и 4 см, потому что (2 + 4) · 2 = 6 · 2 = 12 см
3 см и 3 см, потому что (3 + 3) · 2 = 6 · 2 = 12 см
Получается, чтобы понять, какой прямоугольник начертить, нужно понять, площадь какого из этих прямоугольников больше:
S1 = 1 · 5 = 5 см2
S2 = 2 · 4 = 8 см2
S3 = 3 · 3 = 9 см2
Вывод: необходимо начертить прямоугольник с большей площадью в 9 см2 и стороной в 3 см, который ещё является и квадратом.
1) Чтобы вычислить площадь фигуры, нужно понять, какую часть плоскости она занимает в единицах квадратных единицах измерения.
2) У прямоугольника есть две величины, с помощью которых можно площадь прямоугольника вычислить – длина и ширина.
3) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Рассуждаем.
Необходимо начертить прямоугольник с периметром 12 см и наибольшей площадью.
Периметр – сумма длин всех сторон.
Вычислить периметр прямоугольника можно по формуле: (а + b) · 2 – сумма длины и ширины, умноженная на 2.
Значит, (а + b) · 2 = 12, тогда, сумма длин двух сторон (а + b) = 6 см
Продолжаем рассуждения.
Значит, нужно подумать, сумма каких сторон – 6 см.
Варианты сторон:
1 + 5 = 6
4 + 2 = 6
3 + 3 = 6
Продолжаем рассуждения.
Теперь необходимо вычислить площади прямоугольник с такими длинами сторон и выбрать наибольшую.
1 ∙ 5 = 5 см2
4 ∙ 2 = 8 см2
3 ∙ 3 = 9 см2
Получается, что 9 см2 – наибольшая площадь. Значит, стороны равны 3 см, это квадрат.
Оформляем задание в тетрадь.
Нужно начертить прямоугольник – квадрат со стороной 3 см.
3 ∙ 3 = 9 см2 – площадь.
3 ∙ 4 = 12 (см) – периметр.
Номер 7.
Ленту разрезали на 3 части, затем одну из этих частей разрезали еще на 4 части. На сколько всего частей разрезали ленту? Сколько сделали разрезов?
Ответ:
Ленту разрезали на 6 частей. Всего сделали 5 разрезов.
Чтобы ответить на вопрос задачи лучше выполнить реальные действия, т.е. материальную ленту разрезать на 3 части, а потом еще одну на 4 части.
Разделим ленту на 3 части.
Разобьем одну часть на 4 одинаковые части.
Посчитаем количество получившихся частей и разрезов.
Записываем ответ.
Ответ: ленту разрезали на 6 частей, всего сделали 5 разрезов.
Проверим себя и оценим свои достижения
ТЕКСТЫ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Задания базового уровня
Номер 1.
Вычисли.
7 · 8 9 · 6 63 : 9 72 : 8 42 : 6 28 : 7 36 : 4 56 : 8
Ответ:7 · 8 = 56 9 · 6 = 54 63 : 9 = 7 72 : 8 = 9 42 : 6 = 7 28 : 7 = 4 36 : 4 = 9 56 : 8 = 7
Номер 2.
Найди значения выражений.
35 – 40 : 8 76 – (26 + 40) 9 + 81 : 9 28 – (18 + 9) : 3
Ответ:
Номер 3.
Вычисли.
49 + 38 92 – 57
Ответ:
Номер 4.
Для украшения ёлки приготовили 4 коробки с ёлочными игрушками, по 6 игрушек в каждой коробке. Из них на ёлку повесили 20 игрушек. Сколько игрушек осталось в коробках?
Ответ:Было – 4 к. по 6 игр. Повесили – 20 игр. Осталось – ? игр. 1) 6 · 4 = 24 (игр.) – было в коробках. 2) 24 – 20 = 4 (т.) Ответ: 4 игрушки осталось в коробках.
Номер 5.
В школьную столовую привезли 24 кг яблок, а груш в 3 раза меньше. Сколько всего килограммов яблок и груш привезли в школьную столовую?
Ответ:
1) 24 : 3 = 8 (кг) – груш привезли в столовую. 2) 24 + 8 = 32 (кг) Ответ: 32 кг фруктов привезли в столовую.
Номер 6.
Начерти прямоугольник со сторонами 3 см и 4 см. Найди его периметр и площадь.
Ответ:
S = a · b S = 4 · 3 = 12 см P = (a + b) · 2 P = (4 + 3) · 2 = 7 · 2 = 14
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.