Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 108

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 32.
В мастерской было 3 куска тюля – всего 92 м. Длина первого куска 23 м, а второго – 39 м. Сколько метров тюля в третьем куске?
Ответ:I – 23 м
II – 39 м
III – ? м
Всего – 92 м
1-й способ решения:
1) 23 + 39= 62 (м) – в первом и втором куске.
2) 92 – 62 = 30 (м)
Выражение:
92 – (23 + 39) = 30 (м)
2-й способ решения:
1) 92 – 23 = 69 (м) – во втором и третьем куске.
2) 69 – 39 = 30 (м)
Ответ: длина третьего куска тюля составляет 30 метров.
3-й способ решения:
1) 92 – 23 = 69 (м) – длина второго и третьего куска вместе.
2) 69 – 39 = 30 (м) – длина третьего куска.
Ответ: 30 м тюля.
4-й способ решения:
1) 92 – (23 + 39) = 30 (м) – длина третьего куска.
Ответ: 30 м тюля.
Решение задачи сводится к выражению, основанном на правиле вычитания суммы из числа: а – (в + с) = (а – в) – с.
Оформляем условие в виде краткой записи.
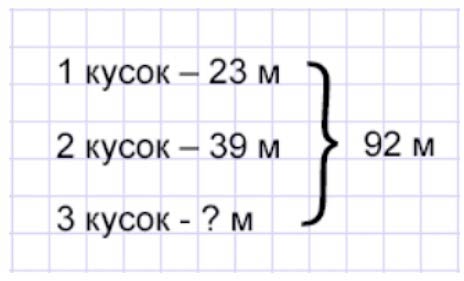
Рассуждаем.
Узнаем сколько метров тюля в первом и втором куске. Чтобы это вычислить нужно количество тюли в первом куске сложить с количеством тюли во втором куске.
23 + 39 = 62 (м) − длина первого и второго куска вместе.
Продолжаем рассуждение.
Общее количество тюля в мастерской складывается из количества тюля в каждом куске. Значит, чтобы узнать, сколько метров тюля в третьем куске, нужно из общего количества тюля вычесть общее количество тюля в двух известных кусках.
92 − 62 = 30 (м) − длина третьего куска.
Записываем ответ.
Ответ: 30 м тюля – длина третьего куска.
Решение выражением:
92 – (23 + 39) = 30 (м), где 23 + 39 – длина первого и второго куска.
Рассмотрим все способы решения задачи.
Решение задачи сводится к выражению: 92 – (23 + 39), основанном на правиле вычитания суммы из числа.
Вычислить значение данного выражения можно тремя способами, поэтому и решения задачи существует три:
Решение 1:
92 – (23 + 39) = 92 – 62 = 30
В первом действии вычисляю количество тюля в двух известных кусках, а во втором – сколько метров тюля в третьем куске.
Решение 2:
92 – (23 + 39) = (92 – 23) – 39 = 69 – 39 = 30
В первом действии вычисляю количество ткани во втором и третьем куске, а во втором – сколько тюля в третьем куске.
Решение 3:
92 – (23 + 39) = (92 – 39) – 23 = 53 – 23 = 30
В первом действии вычисляю количество ткани в первом и третьем куске, а во втором – сколько тюля в третьем куске.
Номер 33.
В марте Нина прочитала 8 сказок, а в апреле – на 2 сказки меньше. Сколько всего сказок она прочитала за эти месяцы?
Ответ:
1-й способ решения:
1) 8 – 2 = 6 (ск.) – в апреле.
2) 8 + 6 = 14 (ск.)
Выражение:
8 + (8 – 2) = 14 (ск.)
Ответ: 14 сказок всего прочитала Нина.
2-й способ решения:
8 + (8 – 2) = 14 (с.) – всего прочитала.
Ответ: 14 сказок.
1) «на 2 сказки меньше», значит, вычисляется вычитанием.
2) «всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.

Рассуждаем.
В марте Нина прочитала 8 сказок, а в апреле – на 2 сказки меньше. На 2 сказки меньше, значит, столько же, сколько в марте, но без 2 сказок.
Чтобы узнать, сколько сказок Нина прочитала в апреле, нужно из количества сказок, прочитанных в марте вычесть 2 сказки.
8 − 2 = 6 (ск.) – прочитала Нина в апреле.
Продолжаем рассуждение.
Общее количество сказок, прочитанных за эти месяцы складывается из количества сказок, прочитанных в марте и апреле. Соответственно, чтобы узнать, сколько сказок прочитала Нина за оба месяца, нужно сложить количество прочитанных сказов в каждый из дней.
8 + 6 = 14 (ск.) − всего прочитала.
Записываем ответ.
Ответ: 14 сказок всего прочитала Нина.
Решение выражением:
8 + (8 – 2) = 14 (ск.), где 8 – 2 – количество сказок, прочитанных в апреле.
Номер 34.
Маме 28 лет, а ее дочке в 7 раз меньше. На сколько лет мама старше дочки?
Ответ:
1-й способ решения:
1) 28 : 7 = 4 (г.) – дочке.
2) 28 – 4 = 24 (г.) – мама старше
Ответ: на 24 года мама старше дочки.
2-й способ решения:
28 – 28 : 7 = 28 – 4 = 24 (года) – на сколько старше.
Ответ: на 24 года.
1) «в 7 раз меньше», значит, вычисляется делением;
2) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
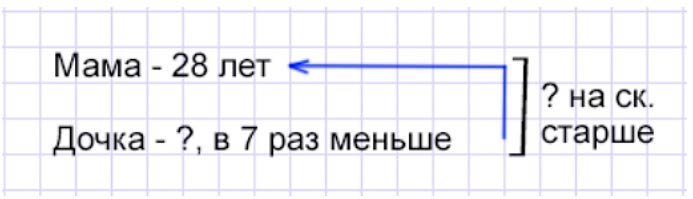
Рассуждаем.
Маме 28 лет, а дочке в 7 раз меньше. Значит, чтобы узнать сколько лет маме, нужно возраст мамы разделить на 7.
28 : 7 = 4 (года) – возраст дочки.
Продолжаем рассуждение.
Мы узнали, что маме – 28 лет, а дочке – 4 года. Чтобы узнать на сколько мама старше дочки, нужно из большего возраста вычесть меньший. То есть, из возраста мамы вычесть возраст дочки.
28 − 4 = 24 (года) – на сколько мама старше дочки.
Записываем ответ.
Ответ: на 24 года мама старше дочки.
Решение выражением:
28 – 28 : 7 = 24 (года), где 28 : 7 – возраст дочери.
Номер 35.
Составь по кратким записям задачи и реши их.

Задача 1:
На прилавке было 25 кг картофеля и 10 кг свёклы. За день продали 18 кг овощей. Сколько килограмм овощей осталось на прилавке?
(25 + 10) − 18 = 17 (кг) – овощей осталось.
Ответ: 17 кг овощей осталось на прилавке.
Задача 2:
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. После того как он сходил в магазин у него осталось 34 рубля. Сколько рублей истратил Коля?
(50 + 10) − 34 = 26 (руб.) – истратил Коля.
Ответ: 26 рублей истратил Коля в магазине.
1) Задача 1:
На прилавке было 25 кг картофеля и 10 кг свёклы. За день продали 18 кг овощей. Сколько килограмм овощей осталось на прилавке?
2) Задача 2:
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. После того как он сходил в магазин у него осталось 34 рубля. Сколько рублей истратил Коля?
Оформляем условие в виде краткой записи.
Было – 25 кг и 10 кг
Продали – 18 кг
Осталось – ?
Рассуждаем.
На прилавке было 25 кг картофеля и 10 кг свеклы. Общее количество овощей складывается из количества овощей каждого вида. Значит, чтобы узнать, сколько овощей было на прилавке, нужно сложить количество картофеля и свёклы.
25 + 10 = 35 (кг) – было всего овощей.
Продолжаем рассуждение.
За день продали 18 кг овощей, значит их стало меньше. Общее количество овощей складывается из количества проданных овощей и оставшихся.
Чтобы узнать, сколько овощей осталось, нужно из общего количества овощей вычесть количество проданных.
35 – 18 = 17 (кг) – осталось.
Записываем ответ.
Ответ: 17 кг осталось овощей.
Решение выражением:
(25 + 10) – 18 = 17 (кг), где 25 + 10 – общее количество овощей.
Рассмотрим все способы решения задачи.
Вычислить значение данного выражения можно двумя способами, поэтому и решения задачи существует два:
Решение 1:
(25 + 10) – 18 = 35 – 18 = 17
В первом действии вычисляем, сколько овощей было на прилавке, а во втором – сколько овощей осталось.
Решение 2:
(25 + 10) – 18 = (25 – 18) + 10 = 7 + 10 = 17
В первом действии вычисляем количество оставшегося картофеля, а во втором – сколько всего овощей осталось.
Оформляем условие в виде краткой записи.
Было – 50 р. и 10 р.
Истратили – ?
Осталось – 34 р.
Рассуждаем.
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. Значит, общее количество денег складывается из количества денег обоих видов. Чтобы узнать, сколько денег было у Коли, нужно сложить количество денег Коли.
50 + 10 = 60 (р.) – было всего денег.
Продолжаем рассуждение.
Коля сходил в магазин и у него осталось 34 рубля. При этом общее количество денег складывается из количества денег потраченных и оставшихся. Соответственно, чтобы узнать, сколько овощей потратил Коля, нужно из общего количества денег вычесть количество потраченных.
60 – 34 = 36 (р.) – денег истратил Коля.
Записываем ответ.
Ответ: 26 рублей истратил Коля.
Решение выражением:
(50 + 10) – 34 = 26 (руб.), где 50 + 10 – общее количество денег.
Рассмотрим все способы решения задачи.
Вычислить значение данного выражения можно двумя способами, поэтому и решения задачи существует два:
Решение 1:
(50 + 10) – 34 = 60 – 34 = 26
В первом действии вычисляем количество денег Коли, а во втором – сколько денег он потратил.
Решение 2:
(50 + 10) – 34 = (50 – 34) + 10 = 16 + 10 = 26
В первом действии вычисляем количество оставшихся бумажных денег, а во втором – сколько денег потратил Коля.
Номер 36.
Вычисли и выполни проверку.
Ответ:
Вспомни зависимость между компонентами и результатом действия вычитания, сложения.
Выполним устные рассуждения.
Вычислим 75 – 27
Вычитаем единицы. От числа 5 мы не можем отнять 7.
Занимаем 1 дес. = 10 ед., 10 + 5 = 15 ед., 15 – 7 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 7 дес., мы занимали 1 дес, осталось 7 – 1 = 6 дес.,
6 – 2 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 48.
Вычислим 39 + 28
Складываем единицы. 9 + 8 = 17 – получилось 1 дес. и 7 ед.
Записываем в разряде единиц число 7, а 1 дес. запоминаем.
Складываем десятки. 3 + 2 = 5 и ещё 1 дес., который запомнили 5 + 1 = 6 – получилось десяток.
Записываем в разряде десятков число 6.
Читаем ответ: 67.
Вычисляем 96 – 49
Вычитаем единицы. От числа 6 мы не можем отнять 9.
Занимаем 1 дес. = 10 ед., 10 + 6 = 16 ед., 16 – 9 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 9 дес., мы занимали 1 дес, осталось 9 – 1 = 8 дес.,
8 – 4 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 47.
Вычисляем 17 + 36
Складываем единицы. 7 + 6 = 13 – получилось 1 дес. и 3 ед.
Записываем в разряде единиц число 3, а 1 дес. запоминаем.
Складываем десятки. 1 + 3 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 53.
Оформляем задание в тетрадь.
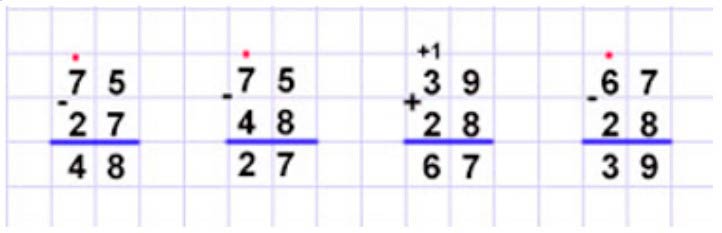
Сделаем проверку.
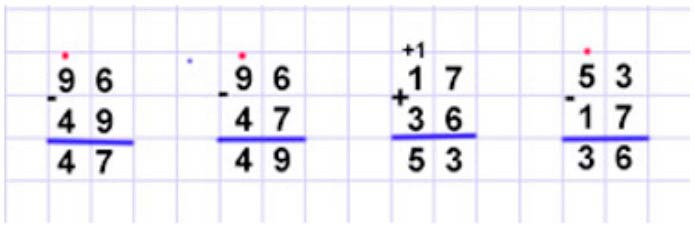
Номер 37.
Реши уравнения.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания, сложения, умножения, деления.
Рассуждаем.
36 – х = 14,
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
х · 26 = 26,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х + 20 = 48,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х – 0 = 19,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х – 44 = 18,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х : 1 = 24,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Решим уравнения.
36 − x = 14
x = 36 − 14
x = 22
x ∙ 26 = 26
x = 26 : 26
x = 1
x + 20 = 48
x = 48 − 20
x = 28
x − 0 = 19
x = 19 + 0
x = 19
x − 44 = 18
x = 18 + 44
x = 62
x : 1 = 24
x = 24 ∙ 1
x = 24
Сделаем проверку.
36 − x = 14
Проверка: вместо х подставим число 22.
36 – 22 = (30 – 20) + (6 – 2) = 10 + 4 = 14
14 = 14 – верно.
x ∙ 26 = 26
Проверка: вместо х подставим число 1.
1 · 26 = 26,
так как при умножении любого числа на 1, получаем тоже самое число.
26 = 26 – верно.
x + 20 = 48
Проверка: вместо х подставим число 28.
28 + 20 = (20 + 20) + (8 + 0) = 40 + 8 = 48
48 = 48 – верно.
x − 0 = 19
Проверка: вместо х подставим число 10.
19 – 0 = 19,
так как если из числа вычесть 0, то число не изменится.
19 = 19 – верно.
x − 44 = 18
Проверка: вместо х подставим число 62.
62 – 44 = 62 – (42 + 2) = (62 – 42) – 2 = 20 – 2 = 18
18 = 18 – верно.
x : 1 = 24
Проверка: вместо х подставим число 24.
24 : 1 = 24,
так как если число разделить на 1, то получим тоже самое число.
24 = 24 – верно.
Оформляем задание в тетрадь.
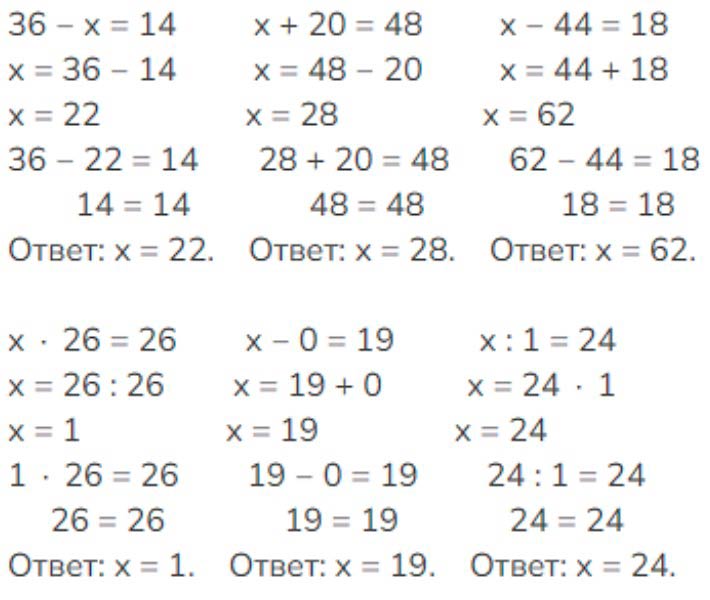
Номер 38.
Найди значения выражений b + c и b − c при b = 30 и c = 14, b = 27 и c = 19.
Ответ:
1) в + с, сумма, значит, вычисляется сложением.
2) в – с, разность, значит, вычисляется вычитанием.
Промежуточные вычисления.
b + с,
если b = 30, c = 14
30 + 14 = (30 + 10) + 4 = 40 + 4 = 44
Складываем по разрядам: единицы складываем с единицами, а десятки - с десятками.
если b = 27, c = 19
27 + 19 = 27 + (13 + 6) = (27 + 13) + 6 = 40 + 6 = 46
Число 19 разложим на сумму чисел 13 и 6. Вначале к числу 27 прибавим число 13, а потом прибавим число 6.
b – с,
если b = 30, c = 14
30 – 14 = 30 – (10 + 4) = (30 – 10) – 4 = 20 – 4 = 16
Число 14 разложим на сумму чисел 10 и 4. Вначале из числа 30 вычтем число 10, а потом число 4.
b = 27, c = 19
27 – 19 = 27 – (17 + 2) = (27 – 17) – 2 = 10 – 2 = 8
Разложим число 19 на сумму чисел 17 и 2. Вначале из числа 27 вычтем число 17, а потом число 2.
Оформляем задание в тетрадь.
При b = 30 и с = 14, то:
b + с = 30 + 14 = 44
b – c = 30 – 14 = 16.
При b = 27 и с = 19, то:
b + с = 27 + 19 = 46
b – c = 27 – 19 = 8.
Номер 39.
Найди длину ломаной и начерти отрезок такой же длины.

2 + 4 + 3 = 9 (см)

1) Ломаная линия – геометрическая фигура, состоящая из звеньев-отрезков, не лежащих на одной прямой.
2) Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками.
3) Длина отрезка – расстояние между точками.
Измерим длину ломанной.
АВСК – ломанная.
С поощоью линейки измерим звенья ломанной.
АВ = 2 см
ВС = 4 см
СК = 3 см
2 см + 4 см + 3 см = 9 см − длина ломаной.
Начертим отрезок.
Так как длина ломанной равна 9 см, то начертим отрезок длиной так же 9 см.

Номер 40.
Проверь себя. Заметь время по часам и выясни, сможешь ли ты правильно выполнить за 2 мин вычисления, записав только ответы.
Ответ:
1 столбик:
12, 30, 63, 48, 18, 32, 45.
2 столбик:
3, 3, 4, 7, 5, 8, 8.
3 столбик:
56, 18, 49, 72, 20, 27, 40.
4 столбик:
9, 7, 3, 8, 6, 9, 4.
1) Окружность – это граница круга, расположенная на плоскости.
2) Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
Начертим окружность.
Окружность чертим с помощью циркуля.
Измеряем расстояние между острым концом и ножкой циркуля 2 см.
Для этого острый конец циркуля должен оставаться в одной точке и расстояние между ножками циркуля не должно меняться.
Окружность состоит из точек, которые равноудалены от одной заданной точки. Это точка называется центром окружности – точка О.
Проведём оси симметрии.
Осей симметрии у окружности бесконечно много. Проведём несколько из них, для примера.
Синими линиями показаны оси симметрии.
Номер 33.
В марте Нина прочитала 8 сказок, а в апреле – на 2 сказки меньше. Сколько сказок Нина прочитала в мае, если за эти три месяца она прочитала 23 сказки?
Ответ:
1) 8 – 2 = 6 (ск.) – прочитала в апреле 2) 8 + 6 = 14 (ск.) – прочитала за 2 месяца 3) 23 – 14 = 9 (ск.) – прочитала в мае Ответ: 9 сказок прочитала Нина в мае
1) «на 2 сказки меньше», значит, вычисляется вычитанием.
2) «всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Чтобы узнать, сколько сказок Нина прочитала в апреле, нужно из количества сказок, прочитанных в марте вычесть 2 сказки.
1) 8 − 2 = 6 (ск.) – прочитала Нина в апреле.
Продолжаем рассуждение.
Чтобы узнать, сколько сказок прочитала Нина за март и апрель вместе, нужно сложить количество прочитанных сказов в каждый из месяцов.
2) 8 + 6 = 14 (ск.) − прочитала за 2 месяца.
Продолжаем рассуждение.
Чтобы узнать, сколько сказок Нина прочитала в мае, нужно из всего количества прочитанных сказок вычесть сказки, которые Нина прочитала в марте и апреле.
3) 23 – 14 = 9 (ск.)
Записываем ответ.
Ответ: 9 сказок.
Номер 34.
Маме 28 лет, а ее дочке в 7 раз меньше. На сколько лет мама старше дочки?
Ответ:
1) 28 : 7 = 4 (г.) – дочке. 2) 28 − 4 = 24 (г.) Ответ: на 24 года мама старше дочки.
1) «в 7 раз меньше», значит, вычисляется делением.
2) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Маме 28 лет, а дочке в 7 раз меньше. Значит, чтобы узнать сколько лет маме, нужно возраст мамы разделить на 7.
28 : 7 = 4 (года) – возраст дочки.
Продолжаем рассуждение.
Мы узнали, что маме – 28 лет, а дочке – 4 года. Чтобы узнать на сколько мама старше дочки, нужно из большего возраста вычесть меньший. То есть, из возраста мамы вычесть возраст дочки.
28 − 4 = 24 (года) – на сколько мама старше дочки.
Записываем ответ.
Ответ: на 24 года мама старше дочки.
Решение выражением: 28 – 28 : 7 = 24 (года), где 28 : 7 – возраст дочери.
Номер 35.
Составь по кратким записям задачи и реши их.

Задача 1:
На прилавке было 25 кг картофеля и 10 кг свёклы. За день продали 18 кг овощей. Сколько килограмм овощей осталось на прилавке?
(25 + 10) − 18 = 17 (кг) – овощей осталось.
Ответ: 17 кг овощей осталось на прилавке.
Задача 2:
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. После того как он сходил в магазин у него осталось 34 рубля. Сколько рублей истратил Коля?
(50 + 10) − 34 = 26 (руб.) – истратил Коля.
Ответ: 26 рублей истратил Коля в магазине.
1) Задача 1:
На прилавке было 25 кг картофеля и 10 кг свёклы. За день продали 18 кг овощей. Сколько килограмм овощей осталось на прилавке?
2) Задача 2:
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. После того как он сходил в магазин у него осталось 34 рубля. Сколько рублей истратил Коля?
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
На прилавке было 25 кг картофеля и 10 кг свеклы. Общее количество овощей складывается из количества овощей каждого вида. Значит, чтобы узнать, сколько овощей было на прилавке, нужно сложить количество картофеля и свёклы.
25 + 10 = 35 (кг) – было всего овощей.
Продолжаем рассуждение.
За день продали 18 кг овощей, значит их стало меньше. Общее количество овощей складывается из количества проданных овощей и оставшихся.
Чтобы узнать, сколько овощей осталось, нужно из общего количества овощей вычесть количество проданных.
35 – 18 = 17 (кг) – осталось.
Записываем ответ.
Ответ: 17 кг осталось овощей.
Решение выражением: (25 + 10) – 18 = 17 (кг), где 25 + 10 – общее количество овощей.
Рассмотрим все способы решения задачи.
Вычислить значение данного выражения можно двумя способами, поэтому и решения задачи существует два:
Решение 1:
(25 + 10) – 18 = 35 – 18 = 17
В первом действии вычисляем, сколько овощей было на прилавке, а во втором – сколько овощей осталось.
Решение 2:
(25 + 10) – 18 = (25 – 18) + 10 = 7 + 10 = 17
В первом действии вычисляем количество оставшегося картофеля, а во втором – сколько всего овощей осталось.
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
У Коли было 50 рублей бумажной купюрой и 10 рублей монетами. Значит, общее количество денег складывается из количества денег обоих видов. Чтобы узнать, сколько денег было у Коли, нужно сложить количество денег Коли.
50 + 10 = 60 (р.) – было всего денег.
Продолжаем рассуждение.
Коля сходил в магазин и у него осталось 34 рубля. При этом общее количество денег складывается из количества денег потраченных и оставшихся. Соответственно, чтобы узнать, сколько овощей потратил Коля, нужно из общего количества денег вычесть количество потраченных.
60 – 34 = 36 (р.) – денег истратил Коля.
Записываем ответ.
Ответ: 26 рублей истратил Коля.
Решение выражением: (50 + 10) – 34 = 26 (руб.), где 50 + 10 – общее количество денег.
Рассмотрим все способы решения задачи.
Вычислить значение данного выражения можно двумя способами, поэтому и решения задачи существует два:
Решение 1:
(50 + 10) – 34 = 60 – 34 = 26
В первом действии вычисляем количество денег Коли, а во втором – сколько денег он потратил.
Решение 2:
(50 + 10) – 34 = (50 – 34) + 10 = 16 + 10 = 26
В первом действии вычисляем количество оставшихся бумажных денег, а во втором – сколько денег потратил Коля.
Номер 36.
Вычисли и выполни проверку.
75 – 27 39 + 28 96 – 49 17 + 34
Ответ:
Вспомни зависимость между компонентами и результатом действия вычитания, сложения.
Выполняем устные рассуждения.
Вычислим 75 – 27
Вычитаем единицы. От числа 5 мы не можем отнять 7.
Занимаем 1 дес. = 10 ед., 10 + 5 = 15 ед., 15 – 7 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 7 дес., мы занимали 1 дес, осталось 7 – 1 = 6 дес.,
6 – 2 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 48.
Вычислим 39 + 28
Складываем единицы. 9 + 8 = 17 – получилось 1 дес. и 7 ед.
Записываем в разряде единиц число 7, а 1 дес. запоминаем.
Складываем десятки. 3 + 2 = 5 и ещё 1 дес., который запомнили 5 + 1 = 6 – получилось десяток.
Записываем в разряде десятков число 6.
Читаем ответ: 67.
Вычисляем 96 – 49
Вычитаем единицы. От числа 6 мы не можем отнять 9.
Занимаем 1 дес. = 10 ед., 10 + 6 = 16 ед., 16 – 9 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 9 дес., мы занимали 1 дес, осталось 9 – 1 = 8 дес.,
8 – 4 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 47.
Вычисляем 17 + 36
Складываем единицы. 7 + 6 = 13 – получилось 1 дес. и 3 ед.
Записываем в разряде единиц число 3, а 1 дес. запоминаем.
Складываем десятки. 1 + 3 = 4 и ещё 1 дес., который запомнили 4 + 1 = 5 – получилось десяток.
Записываем в разряде десятков число 5.
Читаем ответ: 53.
Оформляем задание в тетрадь.
-(2023).jpg)
Делаем проверку.
-(2023).jpg)
Номер 37.
Реши уравнения.
36 – x = 14 x · 26 = 26 x + 20 = 48 x – 0 = 19 x – 44 = 18 x : 1 = 24
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания, сложения, умножения, деления.
Рассуждаем.
36 – х = 14,
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
х · 26 = 26,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х + 20 = 48,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х – 0 = 19,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х – 44 = 18,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х : 1 = 24,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Решим уравнения.
36 − x = 14
x = 36 − 14
x = 22
x ∙ 26 = 26
x = 26 : 26
x = 1
x + 20 = 48
x = 48 − 20
x = 28
x − 0 = 19
x = 19 + 0
x = 19
x − 44 = 18
x = 18 + 44
x = 62
x : 1 = 24
x = 24 ∙ 1
x = 24
Сделаем проверку.
36 − x = 14
Проверка: вместо х подставим число 22.
36 – 22 = (30 – 20) + (6 – 2) = 10 + 4 = 14
14 = 14 – верно.
x ∙ 26 = 26
Проверка: вместо х подставим число 1.
1 · 26 = 26,
так как при умножении любого числа на 1, получаем тоже самое число.
26 = 26 – верно.
x + 20 = 48
Проверка: вместо х подставим число 28.
28 + 20 = (20 + 20) + (8 + 0) = 40 + 8 = 48
48 = 48 – верно.
x − 0 = 19
Проверка: вместо х подставим число 10.
19 – 0 = 19,
так как если из числа вычесть 0, то число не изменится.
19 = 19 – верно.
x − 44 = 18
Проверка: вместо х подставим число 62.
62 – 44 = 62 – (42 + 2) = (62 – 42) – 2 = 20 – 2 = 18
18 = 18 – верно.
x : 1 = 24
Проверка: вместо х подставим число 24.
24 : 1 = 24,
так как если число разделить на 1, то получим тоже самое число.
24 = 24 – верно.
Оформим задание в тетрадь.
.jpg)
Номер 38.
Найди значения выражений b + c и b − c при b = 30 и c = 14, b = 27 и c = 19.
Ответ:
1) в + с, сумма, значит, вычисляется сложением.
2) в – с, разность, значит, вычисляется вычитанием.
Промежуточные вычисления.
b + с,
если b = 30, c = 14
30 + 14 = (30 + 10) + 4 = 40 + 4 = 44
Складываем по разрядам: единицы складываем с единицами, а десятки - с десятками.
если b = 27, c = 19
27 + 19 = 27 + (13 + 6) = (27 + 13) + 6 = 40 + 6 = 46
Число 19 разложим на сумму чисел 13 и 6. Вначале к числу 27 прибавим число 13, а потом прибавим число 6.
b – с,
если b = 30, c = 14
30 – 14 = 30 – (10 + 4) = (30 – 10) – 4 = 20 – 4 = 16
Число 14 разложим на сумму чисел 10 и 4. Вначале из числа 30 вычтем число 10, а потом число 4.
b = 27, c = 19
27 – 19 = 27 – (17 + 2) = (27 – 17) – 2 = 10 – 2 = 8
Разложим число 19 на сумму чисел 17 и 2. Вначале из числа 27 вычтем число 17, а потом число 2.
Оформляем задание в тетрадь.
При b = 30 и с = 14, то:
b + с = 30 + 14 = 44
b – c = 30 – 14 = 16.
При b = 27 и с = 19, то:
b + с = 27 + 19 = 46
b – c = 27 – 19 = 8.
Номер 39.
Найди длину ломаной и начерти отрезок такой же длины.

2 + 4 + 3 = 9 (см)

1) Ломаная линия – геометрическая фигура, состоящая из звеньев-отрезков, не лежащих на одной прямой.
2) Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками.
3) Длина отрезка – расстояние между точками.
Измерим длину ломанной.
АВСК – ломанная.
С поощоью линейки измерим звенья ломанной.
АВ = 2 см
ВС = 4 см
СК = 3 см
2 см + 4 см + 3 см = 9 см − длина ломаной.
Начертим отрезок.
Так как длина ломанной равна 9 см, то начертим отрезок длиной так же 9 см.
.jpg)
Номер 40.
Начерти в тетради окружность с центром в точке О радиусом 2 см. Проведи в окружности 4 оси симметрии.
Ответ:
1) Окружность – это граница круга, расположенная на плоскости.
2) Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
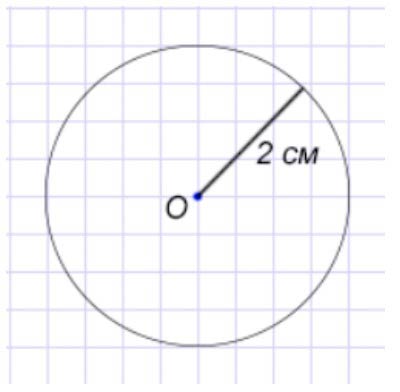
Начертим окружность.
Окружность чертим с помощью циркуля.
Измеряем расстояние между острым концом и ножкой циркуля 2 см.
Для этого острый конец циркуля должен оставаться в одной точке и расстояние между ножками циркуля не должно меняться.
Окружность состоит из точек, которые равноудалены от одной заданной точки. Это точка называется центром окружности – точка О.
-(2023).jpg)
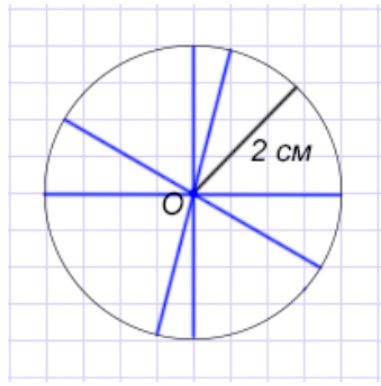
Проведём оси симметрии.
Осей симметрии у окружности бесконечно много. Проведём несколько из них, для примера.
-(2023).jpg)
Синими линиями показаны оси симметрии.
Номер 41.
Проверь себя. Cможешь ли ты правильно выполнить за 2 мин вычисления, записывая только ответы?
4 · 3 6 : 2 7 · 8 27 : 3 6 · 5 12 : 4 3 · 6 56 : 8 9 · 7 36 : 9 7 · 7 15 : 5 6 · 8 42 : 6 8 · 9 64 : 8 2 · 9 25 : 5 4 · 5 36 : 6 8 · 4 24 : 3 9 · 3 81 : 9
Ответ:1 столбик: 12, 30, 63, 48, 18, 32 2 столбик: 3, 3, 4, 7, 5, 8 3 столбик: 56, 18, 49, 72, 20, 27 4 столбик: 9, 7, 3, 8, 6, 9
В случае затруднения обращайся к таблице умножения и деления на форзаце учебника.
Рассуждаем.
Перед тем как начать вычислять поставь повтори таблицу умножения и таймер на часах 2 минуты. Постарайся уложиться за это время. Если не получается, попробуй ещё раз.
Записываем ответы в тетрадь.
1 столбик: 12, 30, 63, 48, 18, 32, 45.
2 столбик: 3, 3, 4, 7, 5, 8, 8.
3 столбик: 56, 18, 49, 72, 20, 27, 40.
4 столбик: 9, 7, 3, 8, 6, 9, 4.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.