Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 106

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 17.
Из одной третьей части бруска красного пластилина вылепили 4 одинаковые вышенки. Сколько таких вишенок можно вылепить из целого бруска пластилина?
Ответ:
4 ∙ 3 = 12 (в.) вишенок можно слепить Ответ: 12 вишенок можно слепить из целого бруска пластилина.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде чертежа.
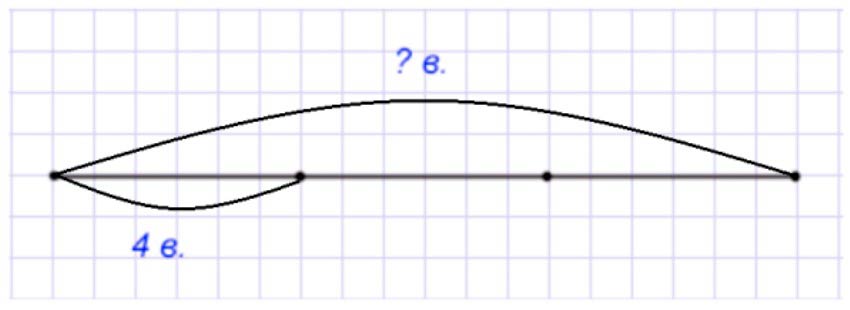
Рассуждаем.
Из одной третьей части бруска вылепили 4 одинаковые вишенки. Значит, весь брусок разделили на 3 части, а взяли только одну. И из этого куска были сделаны 4 одинаковые вишенки.
Соответственно, чтобы узнать, сколько всего вишенок можно вылепить из бруска пластилина, нужно количество вишенок, которые можно вылепить из одной части умножить на количество частей.
4 ∙ 3 = 12 (в.) − из целого бруска.
Записываем ответ.
Ответ: 12 вишенок можно слепить из целого бруска пластилина.
Номер 18.
Заполни пропуски.
Ответ:Одна четвертая часть года – это 3 мес. 12 : 4 = 3. Одна шестая часть суток – это 4 ч. 24 : 6 = 4. Одна десятая часть часа – это 6 мин. 60 : 10 = 6.
1) Помни о том, какие существуют единицы измерения времени: день, неделя, месяц, год.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформим условие в виде чертежа.
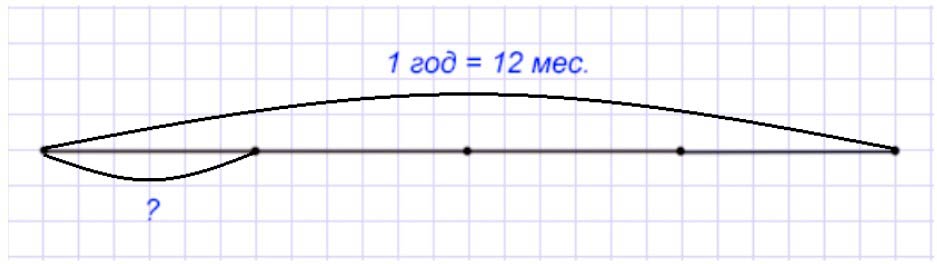
Рассуждаем.
Год – это целое – 12 месяцев. Нужно узнать одну четвертую часть года, значит год разбиваем на 4 части и берем только одну.
12 : 4 = 3 месяца,
Значит, одна четвертая часть года – 3 месяца.
Оформим условие в виде чертежа.
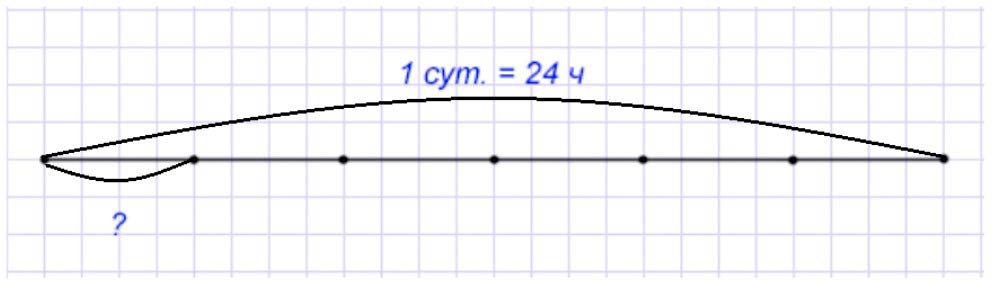
Рассуждаем.
Сутки – это целое – 24 часа. Нужно узнать шестую часть суток, значит сутки разбиваем на 6 частей, а возьмем только одну.
24 : 6 = 4 часа,
Значит, одна шестая часть суток – 4 часа.
Оформим условие в виде чертежа.
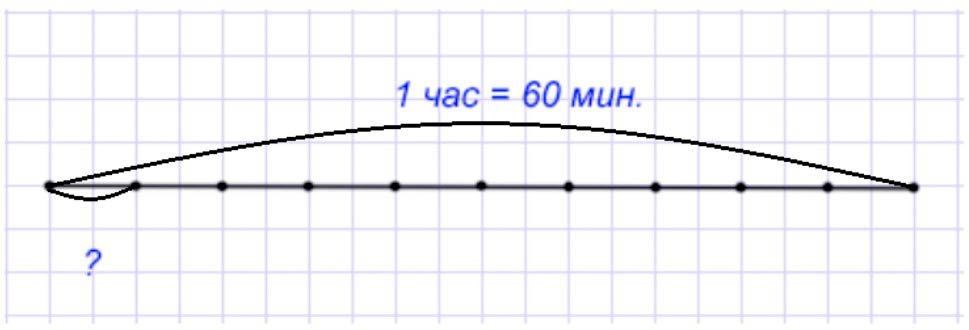
Рассуждаем.
Час – это целое – это 60 минут. Нужно узнать одну десятую часть часа, значит час разобьем на 10 частей, а возьмем только одну, 60 : 10 = 6 минут.
Значит, одна десятая часть часа – 6 минут.
Вычисляем.
Год – 12 месяцев.
12 : 4 = 3 (м.) – четвертая часть года.
Сутки – 24 часа.
24 : 6 = 4 (ч.) – шестая часть чуток.
Час – 60 минут.
60 : 10 = 6 (мин.) – десятая часть часа.
Заполняем пропуски.
Одна четвертая часть года – это 3 мес.
Одна шестая часть суток – это 4 ч.
Одна десятая часть часа – это 6 мин.
Номер 19.
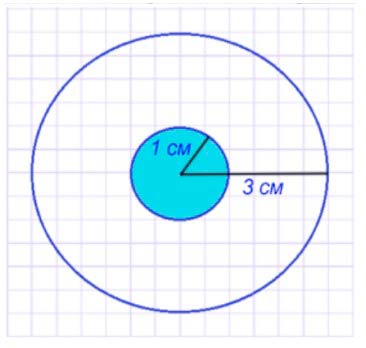
Начерти две окружности с одним центром так, чтобы радиус первой был 3 см, а радиус второй составлял третью часть радиуса первой окружности. Закрась круг с меньшим радиусом.
Ответ:
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Радиус – отрезок, соединяющий центр окружности и любую точку на окружности.
Радиус первой окружности – 3 см, а второй – третья часть радиуса первой.
То есть, 3 см – это целое, делим на 3 части, а берем только одну часть.
3 : 3 = 1 (см) – радиус второй окружности.
Начертим.
Значит, чертим две окружности с центром в одной точке так, чтобы радиус первой окружности – 3 см, а второй – 1 см.
Номер 20.
(Устно.) Скажи, чему равно значение х в каждом из данных уравнений.
Ответ:
36 + х = 36
х = 36 - 36
х = 0
Проверка:
36 + 0 = 36
36 = 36
Ответ:
х = 0
27 : х = 1
х = 27 :1
х = 27
Проверка:
27 : 27 = 1
1 = 1
Ответ:
х = 27
62 · х = 62
х = 62 : 62
х = 1
Проверка:
62 · 1 = 62
62 = 62
Ответ:
х = 1
48 - х = 0
х = 48 - 0
х = 48
Проверка:
48 - 48 = 0
62 = 62
Ответ:
х = 1
1) Помни о том, что при умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
3) Вспомни зависимость между компонентами и результатом действия вычитания, сложения, умножения, деления.
Рассуждаем.
Для выполнения задания решать уравнения не нужно, достаточно проанализировать их и сразу станет понятно значение х.
36 + х = 36
Данное уравнение основано на арифметическом действии сложение. Первое слагаемое равно значению суммы, а второе слагаемое – неизвестно. При этом, первое слагаемое равно значению суммы. Такое возможно только если число увеличивают на 0, значит к числу прибавляют 0.
Значит, х = 0.
48 – х = 0
Данное уравнение основано на арифметическом действии вычитания. При этом уменьшаемое равно 48, а значение разности – 0. Вычитаемое неизвестно. Такое возможно только если из числа вычесть это же число. Получается, х = 48.
27 : х = 1
Данное уравнение основано на действии деления. Делимое равно 27, а значение частного – 1. Делитель неизвестен. Единица при делении получается, только если число делить на это же число.
Получается, х = 27.
х : 9 = 0
Данное уравнение основано на действии деления. Делимое неизвестно, делитель равен 9, а значение частного – 0. 0 при делении числа на число может получится только если 0 делить на любое число.
Значит, х = 0.
62 · х = 62
Данное уравнение основано на действии умножения. Первый множитель равен 62, второй неизвестен, а третий – 62. Первый множитель может быть равен значению произведения, только если число умножают на единицу. Значит, х = 1.
74 : х = 1
Данное уравнение основано на действии деления. Делимое равно 74, а значение частного – 1. Делитель неизвестен. Единица при делении получается, только если число делить на это же число.
Получается, х = 74.
Оформляем задание в тетрадь.
36 + x = 36
x = 0
48 − x = 0
x = 48
27 : x = 1
x = 27
x : 9 = 0
x = 0
62 ∙ x = 62
x = 1
74 : x = 1
x = 74
Номер 21.
На конкурсе «Смекалка» за решение каждой задачи давалось 6 очков, за решение примера – 2 очка. Миша решил 3 задачи и 5 примеров. Сколько очков он набрал?
Ответ:
Всего – ? оч.
1-й способ решения:
6 · 3 + 2 · 5 = 28 (оч.)
Ответ: 28 очков набрал Миша.
2-й способ решения:
6 · 3 + 2 · 5 = 28 (оч.) – всего.
Ответ: 28 очков.
Данная задача: вида «кол-во очков за 1 задание, кол-во заданий, общее кол-во очков» характеризуется зависимостями между компонентами:
Кол-во очков за 1 задание · кол-во заданий = общее кол-во очков.
Общее кол-во очков : кол-во очков за 1 задание = кол-во заданий.
Общее кол-во очков : кол-во заданий = кол-во очков за 1 задание.
Оформляем условие в виде таблицы.

Рассуждаем.
Из задачи видно, что общее количество очков складывается из количества очков за каждую решенную задачу. Значит, чтобы узнать, сколько всего очков заработал Миша за задачи, нужно сложить количество очков за каждую решенную задачу.
Но количество очков, которые дают за 1 задачу одинаковое. Значит, сложение одинаковых слагаемых можно заменить умножением.
3 ∙ 6 = 18 (оч.) – за решённые задачи.
Продолжаем рассуждение.
За каждый пример дают по 2 очка, а решил Миша – 5 примеров. Значит, нам известно количество очков за 1 задание, количество заданий, но неизвестно общее количество очков.
Значит, чтобы узнать, сколько всего очков заработал Миша за примеры, нужно сложить количество очков за каждый решенный пример.
Но количество очков, которые дают за 1 пример одинаковое. Значит, сложение одинаковых слагаемых можно заменить умножением.
2 ∙ 5 = 10 (оч.) – за решённые примеры.
Продолжаем рассуждение.
Общее количество заработанных очков складывается из количества заработанных очков за примеры и задачи. Соответственно, чтобы узнать, сколько всего очков заработал Миша, нужно сложить количество очков, заработанных за примеры и задачи.
18 + 10 = 28 (оч.) – всего набрал Миша.
Записываем ответ.
Ответ: 28 очков набрал Миша.
Решение выражением: 6 · 3 + 2 · 5 = 28 (оч.),
где 6 · 3 – количество очков, заработанных за задачи,
а 2 · 5 – количество очков, заработанных за примеры.
Номер 22.
Назови закрашенные доли круга в порядке их увеличения и в соответствии с этим запиши буквы. Ты получишь зашифрованное слово.

3 = одна шестнадцатая E = одна двенадцатая Р = одна восьмая К = одна шестая А = одна четвертая Л = одна третья О = одна вторая
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Назовем каждую долю.
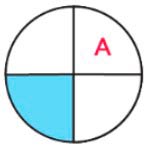
Буква А.
Разбили на 4 части, а закрасили одну такую часть, значит закрашена одна четвертая часть.
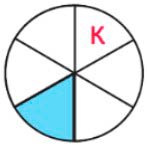
Буква К.
Разбили на 6 частей, а закрасили одну такую часть, значит закрашена одна шестая часть.
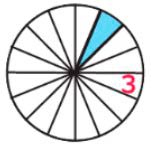
Буква З.
Разбили на 16 частей, а закрасили одну такую часть, значит закрашена одна шестнадцатая часть.
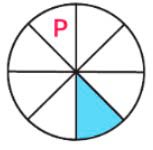
Буква Р.
Разбили на 8 частей, а закрасили одну такую часть, значит закрашена одна восьмая часть.
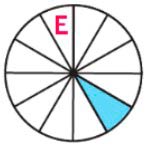
Буква Е.
Разбили на 12 частей, а закрасили одну такую часть, значит закрашена одна двенадцатая часть.
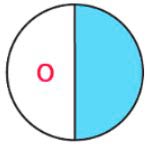
Буква О.
Разбили на 2 части, а закрасили одну такую часть, значит закрашена одна вторая часть.
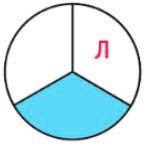
Буква Л.
Разбили на 3 части, а закрасили одну такую часть, значит закрашена одна третья часть.
Расположим доли в порядке увеличения.
Расположим от меньшего к большему. Обрати внимание, что та доля больше, где количество частей, на которые разбили целое, меньше.
3 − одна шестнадцатая часть.
E − одна двенадцатая часть.
Р − одна восьмая часть.
К − одна шестая часть.
А − одна четвертая часть.
Л − одна третья часть.
О − одна вторая часть.
Записываем ответ.
Ответ: Зеркало.
Задание на полях страницы
Ребусы:


Вспомни названия компонентов действия сложения и вычитанием, а также – зависимость между компонентами и результатами действий сложения и вычитания.
Рассуждаем.
Количетво единиц второго слагаемого неизвестно. Но чтобы узнать количество единиц второго слагаемого, нужно из единиц значения суммы вычесть количество единиц первого слагаемого.
Из 6 ед. мы не можем вычесть 7 ед., значит занимаем 1 дес. = 10 ед.,
10 + 6 = 16 ед.
16 ед. – 7 ед. = 9 ед.
Значит, во втором слагаемом 9 единиц.
Продолжаем рассуждение.
Количество десяток в первом слагаемом неизвестно. Но чтобы узнать чему равно количество десятков первого слагаемого, нужно из количества десятков значения суммы вычесть количесвто десятков второго слагаемого.
7 дес. – 2 дес. = 5 дес. и ещё 1 дес. занимали, осталось 5 дес. – 1 дес. = 4 дес.
Значит, в первом слагаемом 4 десятка.
Записываем ответ.
Получим равенство: 47 + 29 = 76.
Запишем равенство в столбик:
.jpg)
Рассуждаем.
Количсетво единиц уменьшаемого неизвестно. Но количсевто единиц уменьшаемого можно узнать, если сложить количество единиц вычитаемого и разности.
Тогда, 5 ед. + 7 ед. = 12 ед – это 1 дес. 2 ед.
Значит, в уменьшаемом 2 единицы.
Продолжаем рассуждение.
Количество десятков вычитаемого неизвестно. Но количество десятков вычитаемого можно узнать, если из количества десятков уменьшаемого вычесть количество десятков значения разности.
8 дес. – 1 дес. = 7 дес. и ещё 1 дес. занимали, осталось 7 дес. – 1 дес. = 6 дес.
Значит, в вычитаемом 6 десятков.
Записываем ответ.
Получим равенство: 82 – 65 = 17.
Запишем равенство в столбик:
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.