Математика 2 класс учебник Моро, Волкова 2 часть ответы – страница 89

- Тип: ГДЗ, Решебник.
- Авторы: Моро М. И., Волкова С. И., Степанова С. В.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 9.
В бассейне занимались три группы пловцов. В первой группе было 12 человек, во второй – на 3 человека меньше, а в третьей – столько, сколько в первой и второй вместе.
Придумай вопрос и реши задачу.

Сколько пловцов в третьей группе?
1) 12 − 3 = 9 (ч.) – во второй группе.
2) 12 + 9 = 21 (ч.) – в третьей группе.
Ответ: 21 человек в третьей группе всего.
Если в задаче есть слова «на... больше», то задача решается сложением, а если « на... меньше», то задача решается вычитанием.
Повтори, как составить краткую запись задачи.
Поставим вопрос к задаче
Вопрос:
Сколько пловцов занимались в третьей группе?
Оформляем условие в виде краткой записи

Рассуждаем
Чтобы узнать, сколько пловцов во второй группе, нужно из количества пловцов в первой группе вычесть 3.
1) 12 − 3 = 9 (ч.) – во второй группе.
Продолжаем рассуждение
Чтобы узнать, сколько пловцов в третьей группе, нужно сложить количество пловцов первой и второй групп вместе.
2) 12 + 9 = 21 (ч.)
Записываем ответ
Ответ: 21 человек в третьей группе.
Номер 10.
Ответ:80 мм = 8 см 28 см = 2 дм 8 см 30 см = 3 дм 65 мм = 6 см 5 мм
Повтори, сколько сантиметров в одном дециметре, сколько миллиметров в одном сантиметре.
Выполняем вычисления
80 мм = 8 см
30 см = 3 дм
28 см = 20 см + 8 см = 2 дм + 8 см = 2 дм 8 см.
65 мм = 60 мм + 5 мм = 6 см + 5 мм = 6 см 5 мм.
Оформляем задание в тетрадь
80 мм = 8 см
30 см = 3 дм
28 см = 2 дм 8 см
65 мм = 6 см 5 мм
Номер 11.
Найди значения:
1) произведения k ∙ 10, если k = 1, k = 3, k = 5, k = 8, k = 10;
2) частного k : 10, если k = 20, k = 60, k = 70, k = 90, k = 100.
1) k ∙ 10
k = 1 1 ∙ 10 = 10
k = 3 3 ∙ 10 = 30
k = 5 5 ∙ 10 = 50
k = 8 8 ∙ 10 = 80
k = 10 10 ∙ 10 = 100
2) k : 10
k = 20 20 : 10 = 2
k = 60 60 : 10 = 6
k = 70 70 : 10 = 7
k = 90 90 : 10 = 9
k = 100 100 : 10 = 10
Повтори, как называются числа при делении и умножении.
Выполняем вычисления
1) k ∙ 10
k = 1 1 ∙ 10 = 10
k = 3 3 ∙ 10 = 30
k = 5 5 ∙ 10 = 50
k = 8 8 ∙ 10 = 80
k = 10 10 ∙ 10 = 100
2) k : 10
k = 20 20 : 10 = 2
k = 60 60 : 10 = 6
k = 70 70 : 10 = 7
k = 90 90 : 10 = 9
k = 100 100 : 10 = 10
Номер 12.
Вычисли и сделай проверку.
Ответ:
Вспомни, как проверить результат сложения и результат вычитания.
Выполняем вычисления

Оформляем задание в тетрадь

Номер 13.
Запиши выражения и вычисли их значения.
1) К сумме чисел 31 и 9 прибавить 14.
2) Из суммы чисел 52 и 8 вычесть 40.
1) (31 + 9) + 14 = 40 + 14 = 54 2) (52 + 8) − 40 = 60 − 40 = 20
Повтори, как называются числа при сложении и вспомни действия с двузначными числами.
Порядок выполнения действий в примерах со скобками.
Выполняем вычисления
1) (31 + 9) + 14 = 40 + 14 = 54
2) (52 + 8) - 40 = 60 - 40 = 20
Номер 14.
На зиму семья заготовила 8 двухлитровых банок компота. Сколько литров компота заготовили?
Составь и реши две задачи, обратные данной.
Заготовили – 8 б. по 2 л
Всего – ? л
1) 8 ∙ 2 = 16 (л) – компота заготовили.
Ответ: 16 литров компота заготовили всего.
Обратная задача 1:
На зиму семья заготовила 16 л компота по 2 л в каждую банку.
Сколько банок компота получилось?
Заготовили – ? б. по 2 л
Всего – 16 л
1) 16 : 2 = 8 (б.) – компота получилось.
Ответ: 8 банок компота по 2 л получилось .
Обратная задача 2:
На зиму семья заготовила 16 л компота в 8 банках.
Сколько литров компота в каждой банке?
Заготовили – 8 б. по ? л
Всего – 16 л
1) 16 : 8 = 2 (л) – компота в одной банке.
Ответ: 2 литра компота в каждой банке.
Повтори, что такое обратная задача.
Оформляем условие в виде краткой записи
Заготовили – 8 б. по 2 л
Всего – ? л
Рассуждаем
Чтобы узнать, сколько литров компота заготовили на зиму, нужно количество банок умножить на количество литров в одной банке.
1) 8 ∙ 2 = 16 (л)
Записываем ответ
Ответ: 16 литров компота заготовили.
Составляем первую задачу обратную данной
На зиму семья заготовила 16 л компота по 2 л в каждую банку.
Сколько банок компота получилось?
Оформляем условие в виде краткой записи
Заготовили – ? б. по 2 л
Всего – 16 л
Рассуждаем
Чтобы узнать, сколько банок компота по 2 литра получилось, нужно все количества компота разделить на 2.
1) 16 : 2 = 8 (б.)
Записываем ответ
Ответ: 8 банок компота получилось.
Составляем вторую задачу обратную данной
На зиму семья заготовила 16 л компота в 8 банках.
Сколько литров компота в каждой банке?
Оформляем условие в виде краткой записи
Заготовили – 8 б. по ? л
Всего – 16 л
Рассуждаем
Чтобы узнать, сколько литров компота в одной банке, нужно все количества компота разделить на количество банок.
1) 16 : 8 = 2 (л)
Записываем ответ
Ответ: 2 литра компота в одной банке.
Номер 15.
Ответ:
(47 − 7) : 2 = 40 : 2 = 20
(84 − 4) : 10 = 80 : 10 = 8
24 − 8 − 8 − 8 = 24 − 24 = 0
12 − 3 − 3 − 3 − 3 = 12 − 12 = 0
Повтори порядок действий при решении числовых выражений со скобками.
Выполняем вычисления
(47 - 7) : 2 = 40 : 2 = 20
(84 - 4) : 10 = 80 : 10 = 8
12 - 3 - 3 - 3 - 3 = 9 - 3 - 3 = 6 - 3 = 0
24 - 8 - 8 - 8 = 16 - 8 - 8 = 8 - 8 = 0
Оформляем задание в тетрадь
(47 − 7) : 2 = 40 : 2 = 20
(84 − 4) : 10 = 80 : 10 = 8
12 − 3 − 3 − 3 − 3 = 12 − 12 = 0
24 − 8 − 8 − 8 = 24 − 24 = 0
Номер 16.
1) Каких фигур на чертеже больше: треугольников или четырехугольников? На сколько?
2) Найди периметр прямоугольника и каждого треугольника, на которые он разделен.
1) На чертеже 5 треугольников и 5 четырёхугольников. Фигур поровну. 5 = 5.
2) Стороны прямоугольника: 20 мм и 26 мм.
20 + 20 + 26 + 26 = 92 мм
Измеряем стороны каждого треугольника в мм и складываем.
Повтори материал о многоугольниках и как определить периметр фигуры.
Посчитаем фигуры на полях страницы и сравним каких фигур больше

Найдем периметры заданных фигур
Прямоугольник образуют треугольники 1 и 2.
Периметр многоугольника равен сумме всех его сторон. В прямоугольнике противоположные стороны равны, тогда, периметр прямоугольника можно найти, умножив сумму двух его соседних сторон на 2. С помощью линейки измеряем стороны прямоугольника, тогда его периметр равен:
(3 + 2) * 2 = 10 (см).
Также с помощью линейки измеряем стороны каждого треугольника, на которые разделён прямоугольник и получаем, что стороны этих треугольников одинаковые, тогда периметр каждого из них равен:
3 + 2 + 4 = 9 (см).
Оформляем задание в тетрадь
Задание 1:
Треугольников 5, четырёхугольников 5.
Одинаковое количество треугольников и четырёхугольников.
Задание 2:
Периметр прямоугольника:
(3 + 2) * 2 = 10 (см)
Периметр каждого треугольника, на которые разделён прямоугольник равен:
3 + 2 + 4 = 9 (см)
Номер 17.
В двух вазах по 18 яблок в каждой. Из первой вазы переложили во вторую 4 яблока. На сколько больше яблок стало во второй вазе, чем в первой?
Ответ:

1) 18 − 4 = 14 (яб.) – осталось в первой вазе.
2) 18 + 4 = 22 (яб.) – стало во второй вазе.
3) 22 − 14 = 8 (яб.) – разница.
Ответ: на 8 яблок стало больше во второй вазе, чем в первой.
Если есть схематический рисунок или чертёж, краткую запись задачи составлять не нужно.
Оформляем условие в виде краткой записи

Рассуждаем
В первой вазе было 18 яблок, из нее переложили 4 яблока во вторую вазу, тогда в первой вазе стало:
1) 18 - 4 = 14 (ябл.) - стало в 1 вазе.
Продолжаем рассуждение
Во второй вазе было 18 яблок, в нее переложили 4 яблока из первой вазы, тогда во второй вазе стало:
2) 18 + 4 = 22 (ябл.) - стало во 2 вазе.
Продолжаем рассуждение
Получается во второй вазе стало больше яблок, чем в первой на
3) 22 - 14 = 8 (ябл.)
Записываем ответ
Ответ: на 8 яблок больше.
Задание внизу страницы
Номер 1.
Вычисли.
7 · 7 – 13 6 · 8 – 23 7 · 9 – 7 · 5
40 – 7 · 4 7 · 9 – 43 8 · 10 – 7 · 8
(21 + 21) : 6 (23 – 16) · 9 10 · (56 – 50)
49
7 · 7 – 13 = 36;
28
40 – 7 · 4 = 12;
42
(21 + 21) : 6 = 7;
48
6 · 8 – 23 = 25;
63
7 · 9 – 43 = 20;
7
(23 – 16) · 9 = 63;
63 35
7 · 9 – 7 · 5 = 28;
80 56
8 · 10 – 7 · 8 = 24;
6
10 · (56 – 50) = 60.
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления
7 · 7 – 13 = 49 – 13 = 36
40 – 7 · 4 = 40 – 28 = 12
(21 + 21) : 6 = 42 : 6 = 7
6 · 8 – 23 = 48 – 23 = 25
7 · 9 – 43 = 63 – 43 = 20
(23 – 16) · 9 = 7 * 9 = 63
7 · 9 – 7 · 5 = 63 – 35 = 28
8 · 10 – 7 · 8 = 80 – 56 = 24
10 · (56 – 50) = 10 * 6 = 60
Оформляем задание в тетрадь
7 · 7 – 13 = 36
40 – 7 · 4 = 12
(21 + 21) : 6 = 7
6 · 8 – 23 = 25
7 · 9 – 43 = 20
(23 – 16) · 9 = 63
7 · 9 – 7 · 5 = 28
8 · 10 – 7 · 8 = 24
10 · (56 – 50) = 60
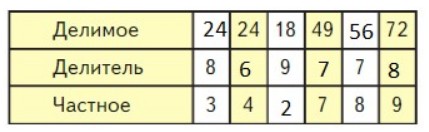
Номер 2.


Вспомним и повторим таблицу умножения.
Рассуждаем и выполняем вычисления
Чтобы найти частное, разделим делимое на делитель:
18 : 9 = 2
Чтобы найти делимое, умножим делитель на частное:
3 * 8 = 24
7 * 8 = 56
Чтобы найти делитель, разделим делимое на частное:
24 : 4 = 6
49 : 7 = 7
72 : 9 = 8
Оформляем задание в тетрадь
Номер 3.
Груз общей массой в 12 кг для доставки разделили поровну для трёх квадрокоптеров. Сколько килограммов груза доставит один квадрокоптер?
Ответ:12 : 3 = 4 (кг) – доставит один квадрокоптер.
Ответ: 4 кг груза доставит один квадрокоптер.
Вспомним и повторим таблицу умножения.
Рассуждаем
Так как вес общего груза для доставки разделили поровну на три квадрокоптера, тогда, чтобы определить вес груза, который перевезет каждый из квадрокоптеров, нужно разделить общий вес на количество квадрокоптеров.
Выполняем вычисления
12 : 3 = 4 (кг)
Записываем ответ
Ответ: 4 кг доставит один квадрокоптер.
Номер 4.
В кафе за шестью столиками сидели по 3 человека, а за тремя столиками – по 4 человека.
Сколько человек было за всеми этими столиками?

1) 3 ∙ 6 = 18 (ч.) – сидели за 6 столами.
2) 4 ∙ 3 = 12 (ч.) – сидели за 3 столами.
3) 18 + 12 = 30 (ч.) – всего.
Ответ: 30 человек всего сидели за столами.
Вспомним из каких частей состоит задача.
Оформляем условие задачи в виде краткой записи
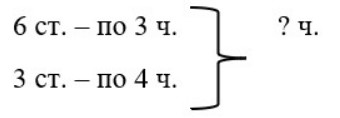
Рассуждаем
Узнаем, сколько человек сидели за шестью столами.
1) 3 ∙ 6 = 18 (ч.) – сидели за 6 столами.
Продолжаем рассуждение
Узнаем, сколько человек сидели за тремя столами.
2) 4 ∙ 3 = 12 (ч.) – сидели за 3 столами.
Продолжаем рассуждение
Узнаем, сколько человек сидели за всеми столами.
3) 18 + 12 = 30 (ч.) – всего.
Записываем ответ
Ответ: 30 человек.
Номер 5.
Начерти 3 отрезка: один длиной 5 см, второй – на 2 см длиннее первого, а третий – в 2 раза длиннее первого.
На сколько сантиметров третий отрезок длиннее второго?
1) 5 + 2 = 7 (см) – длина второго отрезка.
2) 5 ∙ 2 = 10 (см) – длина третьего отрезка.
3) 10 – 7 = 3 (см) – третий отрезок длиннее второго.

Отрезок - это часть прямой, ограниченная с двух сторон.
Вычислим, чему равны длины отрезков
1) 5 + 2 = 7 (см) – длина второго отрезка.
2) 5 ∙ 2 = 10 (см) – длина третьего отрезка.
Начертим отрезки
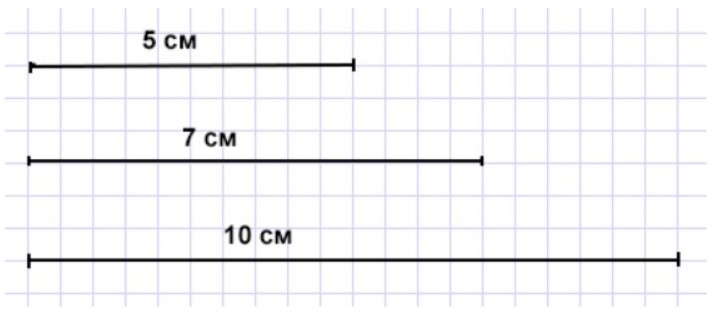
Ответим на вопрос
Узнаем, на сколько см третий отрезок длиннее второго, для этого из длины третьего вычтем длину второго.
10 – 7 = 3 (см) – третий отрезок длиннее второго.
Номер 6.
Вычисли.
25 + 29 38 + 13 57 + 26 64 + 28
21 – 14 43 – 25 40 – 17 54 – 28

1) Помни, что складывать можно только единицы с единицами, а десятки с десятками.
2) Помни вычитать тоже можно только единицы из единиц и десятки из десятков.
3) Помни, что 1 дес. = 10 ед.
Выполняем вычисления
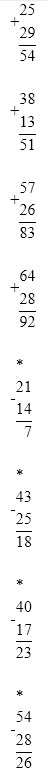
Оформляем задание в тетрадь

Номер 7.
20 〇 16 〇 9 = 27 75 〇 46 〇 6 = 35
38 〇 26 〇 4 = 8 59 〇 7 〇 3 = 49
20 + 16 – 9 = 27;
38 – 26 – 4 = 8;
75 – 46 + 6 = 35;
59 – 7 – 3 = 49.
Равенство – это когда одно количество равно другому.
Выполняем вычисления
20 + 16 – 9 = 36 – 9 = 27
38 – 26 – 4 = 12 – 4 = 8
75 – 46 + 6 = 29 + 6 = 35
59 – 7 – 3 = 52 – 3 = 49
Оформляем задание в тетрадь
20 + 16 – 9 = 36 – 9 = 27
38 – 26 – 4 = 12 – 4 = 8
75 – 46 + 6 = 29 + 6 = 35
59 – 7 – 3 = 52 – 3 = 49
Номер 8.
7 · 3 + 9 9 : 3 + 4 49 – 8 · 5
4 · 7 – 14 14 : 2 · 7 30 – (19 + 7)
21
7 · 3 + 9 = 30;
28
4 · 7 – 14 = 14;
3
9 : 3 + 4 = 7;
7
14 : 2 · 7 = 49;
40
49 – 8 · 5 = 9;
26
30 – (19 + 7) = 4.
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления
7 · 3 + 9 = 21 + 9 = 30
4 · 7 – 14 = 28 – 14 = 14
9 : 3 + 4 = 3 + 4 = 7
14 : 2 · 7 = 7 * 7 = 49
49 – 8 · 5 = 49 – 40 = 9
30 – (19 + 7) = 30 – 26 = 4
Оформляем задание в тетрадь
7 · 3 + 9 = 21 + 9 = 30
4 · 7 – 14 = 28 – 14 = 14
9 : 3 + 4 = 3 + 4 = 7
14 : 2 · 7 = 7 * 7 = 49
49 – 8 · 5 = 49 – 40 = 9
30 – (19 + 7) = 30 – 26 = 4
Задание внизу страницы.
72 : 9 〇 8 8 · 8 〇 60 + 5 81 : 9 〇 10
Ответ:
72 : 9 = 8
8 = 8
8 · 8 < 60 + 5
64 < 65
81 : 9 < 10
9 < 10
Равенство – это когда одно количество равно другому.
Неравенство – это когда одна сторона выражения не равна второй.
Выполняем вычисления
72 : 9 = 8
8 = 8
8 · 8 < 60 + 5
64 < 65
81 : 9 < 10
9 < 10
Оформляем задание в тетрадь
72 : 9 = 8
8 = 8
8 · 8 < 60 + 5
64 < 65
81 : 9 < 10
9 < 10
Задание на полях страницы.
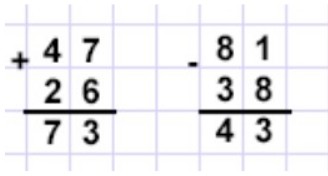
Ребусы:


Повторим алгоритм письменного сложения и вычитания в столбик.
Рассуждаем
1) В разряде единиц: 6 + * > 3, значит, 6 + * = 13, * = 13 - 6 = 7.
В разряде десятков: 4 + * + 1 = 7 , поэтому * = 7 - 4 - 1 = 2.
2) В разряде единиц: * - 8 = 3, поэтому * = 8 + 3 = 11.
В разряде десятков: * = 8 - 3 - 1 = 4.
Выполняем вычисления и оформляем задание в тетрадь
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.