Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – номер 4.141

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Александрова Л.А., Шварцбурд С.И.
- Часть: 1.
- Год: 2020-2024.
- Издательство: Просвещение.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 4.141.
1) С двух станций метро навстречу друг другу движутся два поезда и скорость одного из них на 50 м/мин меньше скорости другого. Сейчас расстояние между ними 6 км 200 м. Найдите скорость каждого поезда, если известно, что они прибудут на одну станцию через 4 мин.
2) Два катера, двигаясь навстречу друг другу, должны встретиться через 6 мин. Сейчас расстояние между ними 4 км 380 м. Найдите скорости этих катеров, если известно, что скорость первого на 70 м/мин меньше скорости второго.
1)

Пусть скорость первого поезда – х м/мин, тогда второго – (х – 50) м/мин.
6 км 200 м = 6200 м.
(х + (х – 50)) · 4 = 6200;
(2х – 50) · 4 = 6200;
2х – 50 = 6200 : 4;
2х – 50 = 1550;
2х = 1550 + 50;
2х = 1600;
х = 1600 : 2;
х = 800.
800 м/мин – скорость первого поезда.
800 – 50 = 750 м/мин – скорость второго поезда.
Ответ: 800м/мин, 750 м/мин.
2)

Пусть скорость первого катера – х м/мин, а второго – (х – 70) м/мин.
4 км 380 м = 4380 м.
((х + (х – 70)) · 6 = 4380;
(2х – 70) · 6 = 4380;
2х – 70 = 4380 : 6;
2х – 70 = 730;
2х = 730 + 70;
2х = 800;
х = 400;
400 м/мин – скорость первого катера.
400 – 70 = 330 м/мин – скорость второго катера.
Ответ: 400 м/мин, 330 м/мин.
Задача а.
Пусть скорость первого поезда – х м/мин, скорость второго поезда на 50 м/мин меньше скорости первого, тогда скорость второго – (х – 50) м/мин.
Поезда движутся навстречу друг другу, значит скорость их сближения можно найти сложением, значит скорость сближения равна (х + х – 50) м/мин.
По условию поезда встретятся через 4 минуты, значит общее расстояние, которое они пройдут будет ((х + х – 50) · 4) м и по условию оно равно 6 км 200 м = 6200 м.
Шаг 1.
Составим краткую запись задачи в виде схематического чертежа:

Составим уравнение и решим его:
(х + х – 50) · 4 = 6200;
Упростим левую часть уравнения, где х + х = 2х.
(2х – 50) · 4 = 6200;
Найдём неизвестный множитель (2х – 50):
2х – 50 = 6200 : 4;
2х – 50 = 1550;
Теперь найдём неизвестное уменьшаемое 2х:
2х = 1550 + 50;
2х = 1600;
Найдём неизвестный множитель х:
х = 1600 : 2;
х = 800.
Значит, 800 м/мин – скорость первого поезда.
Скорость второго поезда на 50 м/мин меньше, значит
800 – 50 = 750 (м/мин) – скорость второго поезда.
Ответ: скорость первого поезда 800 м/мин, скорость второго – 750 м/мин.
Сделаем проверку задачи:
1) 800 + 750 = 1550 (м/мин) – скорость сближения поездов;
2) 6200 : 4 = (4000 + 2000 + 200) : 4 = 1000 + 500 + 50 = 1550 (м/мин) – скорость сближения поездов;
3) 1550 м/мин = 1550 м/мин.
Задача решена верно.
Задача б.
Пусть скорость второго катера – х м/мин, а скорость первого на 70 м/мин меньше скорости второго, значит скорость первого катера (х – 70) м/мин.
Катера движутся навстречу друг другу, значит скорость их сближения можно найти сложением, значит скорость сближения равна (х + х – 70) м/мин.
По условию катера встретятся через 6 минут, значит общее расстояние, которое они пройдут будет ((х + х – 70) · 6) м и по условию оно равно 4 км 380 м = 4380 м.
Шаг 1.
Составим краткую запись задачи в виде схематического чертежа:
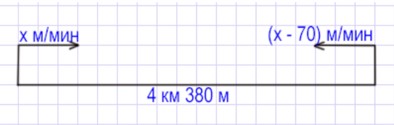
Составим уравнение и решим его:
((х + х – 70) · 6 = 4380;
Упростим левую часть уравнения, где х + х = 2х:
(2х – 70) · 6 = 4380;
Найдём неизвестный множитель (2х – 70):
2х – 70 = 4380 : 6;
2х – 70 = 730;
Теперь найдём неизвестное уменьшаемое 2х:
2х = 730 + 70;
2х = 800;
Найдём неизвестный множитель х:
х = 800 : 2;
х = 400.
Значит, 400 м/мин – скорость второго катера.
Скорость первого катера на 70 м/мин меньше, значит
400 – 70 = 330 (м/мин) – скорость первого катера.
Ответ: скорость первого катера 330 м/мин, скорость второго – 400 м/мин.
Сделаем проверку задачи:
1) 330 + 400 = 730 (м/мин) – скорость сближения катеров;
2) 4380 : 6 = 730(м/мин) – скорость сближения катеров;
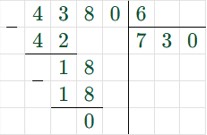
3) 730 м/мин = 730 м/мин.
Задача решена верно.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.