Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 39

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Вариант 2
Номер 1.
Укажи значение выражения а ∙ 500, если а = 60.
Ответ:30000 Значение выражения при а = 60 будет равно 30 000, ведь 60 · 500 = 30 000.
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления.
а ∙ 500 = 60 ∙ 500 = 60 ∙ (5 ∙ 100) = (60 ∙ 5) ∙ 100 = 300 ∙ 100 = 30 000
Выбираем правильный ответ.
Ответ: 30 000.
Номер 2.
Укажи произведение чисел 9000 и 60.
Ответ:540000 Произведение чисел 9000 и 60 равно 540 000, ведь 9000 · 60 = 540 000.
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления.
9 000 ∙ 60 = (9 ∙ 1 000) ∙ 60 = (9 ∙ 60) ∙ 1 000 = 540 ∙ 1 000 = 540 000
Выбираем правильный ответ.
Ответ: 540 000.
Номер 3.
Укажи значение выражения 4 ∙ 8 ∙ 25 ∙ 6
Ответ:4800 Значение выражения 4 · 8 · 25 = 100 · 48 = 4800
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Выполняем вычисления.
4 ∙ 8 ∙ 25 ∙ 6 = (4 ∙ 25) ∙ (8 ∙ 6) = 100 ∙ 48 = 4 800
Выбираем правильный ответ.
Ответ: 4 800.
Номер 4.
Какое число надо умножить на 34, чтобы получить 34000?
Ответ:1000 Чтобы получить 34000, нужно 34 умножить на 1000
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления.
34 000 : 34 = 1 000
Выбираем правильный ответ.
Ответ: 1 000
Номер 5.
Укажи значение выражения а : 30, если а = 2400.
Ответ:80 Значение выражения при а = 2400, равно 80, потому что 2400 : 30 = 80.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления.
2 400 : 30 = 80
Выбираем правильный ответ.
Ответ: 80.
Номер 6.
На какое число разделили 1400, если получили 100?
Ответ:14 число 1400 разделили на 14 и получили 100, ведь 1400 : 14 = 100.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления.
1 400 : 100 = 14
Выбираем правильный ответ.
Ответ: 14.
Номер 7.
Укажи правильно вычисленное произведение чисел 360 и 800.
Ответ:360 ∙ 800 = 288000 Правильно вычислено произведение чисел в первом выражении, потому что второй множитель должен быть записан под десятками первого множителя.
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления.
360 ∙ 800 = 288 000
Выбираем правильный ответ.
Ответ:

Номер 8.
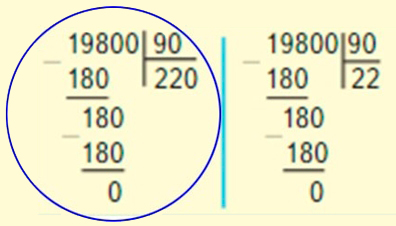
Укажи правильно вычисленное частное чисел 19800 и 90.
Ответ:19800 : 90 = 220 Правильно вычислено частное чисел в первом выражении, потому что ноль делимого необходимо записать в частное.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления.
19 800 : 90 = 220
Выбираем правильный ответ.
Ответ:
Номер 9.
Укажи правильно вычисленное частное и остаток при делении числа 7280 на 600.
Ответ:7280 : 600 = 12 (ост. 80) Правильно вычислен остаток во втором выражении, потому что деление в первом выражении не выполнено до конца.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления.
7 280 : 600 = 12 (ост. 80)
Выбираем правильный ответ.
Ответ:

Номер 10.
Укажи выражение для решения задачи: «Два велосипедиста начали движение одновременно навстречу друг другу по шоссе между двумя городами. Скорость одного велосипедиста 220 м/мин, а другого 250 м/мин. На сколько приблизятся велосипедисты друг к другу через 30 мин?»
Ответ:
(220 + 250) ∙ 30 Для решения задачи подходит третье выражение, потому что сначала необходимо найти скорость сближения, а затем общее расстояние, на которое приблизятся друг к другу велосипедисты. Таким образом, 220 + 250 – скорость сближения; (220 + 250) · 30 – приблизятся друг к другу велосипедисты через 30 минут.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа и выполняем решение.
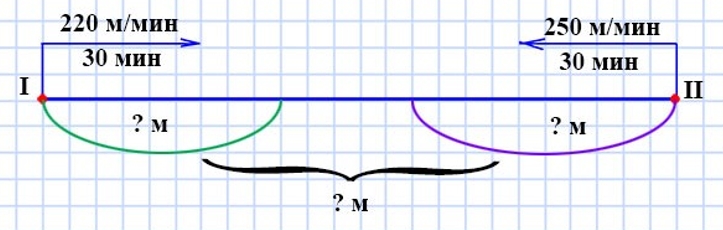
(220 + 250) ∙ 30 = 470 ∙ 30 = 14 100 м = 14 км 100 м – на такое расстояние велосипедисты приблизятся к друг другу.
Выбираем правильный ответ.
Ответ: (220 + 250) ∙ 30
Номер 22.
1) От двух противоположных берегов пруда навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл до встречи со скоростью 8 м/мин, второй – со скоростью 12 м/мин. Найди ширину пруда. 2) Измени задачу, чтобы она решалась так: 200 : 10 – 8 = 12. Ответ: 12 м/мин.
Ответ:
Задача 1:
1) 8 + 12 = 20 (м/мин) – скорость сближения.
2) 20 ∙ 10 = 200 (м) – общая ширина пруда
Выражение:
(12 + 8) ∙ 10 = 200 (м) – общая ширина пруда
Ответ: 200 м ширина пруда.
Задача 2:
От двух берегов пруда, ширина которого 200 м, навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл со скоростью 8 м/мин. Найди скорость второго пловца.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде схематического чертежа.
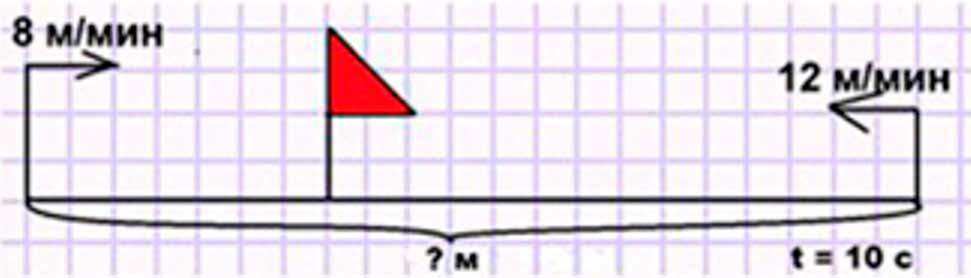
Рассуждаем.
Найдем скорость сближения пловцов. Для этого сложим скорости каждого из них вместе.
8 + 12 = 20 (м/мин) – скорость сближения.
Продолжаем рассуждение.
Чтобы найти ширину пруда, нужно скорость сближения умножить на время в пути.
20 ∙ 10 = 200 (м) – ширина пруда.
Записываем ответ.
Ответ: 200 м ширина пруда.
Шаг 1.
Изменим условие задачи.
От двух берегов пруда, ширина которого 200 м, навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл со скоростью 8 м/мин. Найди скорость второго пловца.
200 : 10 – 8 = 12 (м/мин) – скорость второго пловца.
Ответ: 12 м/мин.
Номер 23.
Составь задачу по чертежу и реши её.

Из двух городов, расстояние между которыми 1200 км, вышли одновременно навстречу друг другу два поезда и встретились через 6 ч. Первый поезд шел со скоростью 98 км/ч. С какой скоростью шел второй поезд?
1-й способ решения:1) 98 ∙ 6 = 588 (км) – проехал первый поезд. 2) 1200 − 588 = 612 (км) – проехал второй поезд. 3) 612 : 6 = 102 (км/ч)
2-й способ решения:1) 1200 : 6 = 200 (км/ч) – скорость сближения. 2) 200 – 98 = 102 (км/ч) – скорость второго поезда
Ответ: 102 км/ч скорость второго поезда.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим схематический чертеж к задаче из учебника.
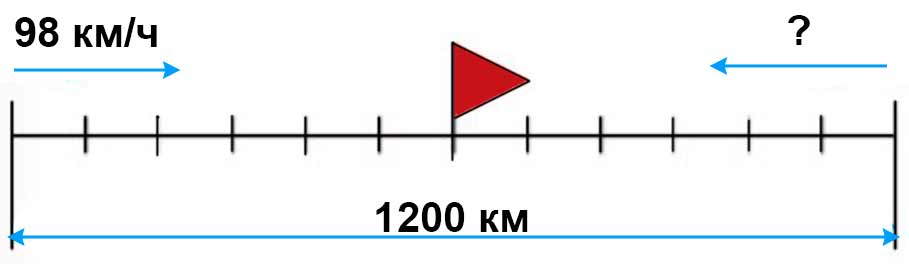
Составляем задачу по чертежу.
Из двух городов, расстояние между которыми 1200 км, вышли одновременно навстречу друг другу два поезда и встретились через 6 ч. Первый поезд шел со скоростью 98 км/ч. С какой скоростью шёл второй поезд?
Рассуждаем.
Найдем скорость сближения поездов, для этого расстояние разделим на время в пути.
1200 : 6 = 200 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать, с какой скоростью шёл второй поезд, нужно из скорости сближения вычесть скорость первого поезда.
200 – 98 = 102 (км/ч) – скорость второго поезда.
Записываем ответ.
Ответ: 102 км/ч скорость второго поезда.
Номер 24.
Грузовая машина прошла 1500 км. Сколько горючего было израсходовано, если на каждые 50 км пути требуется 16 л горючего?
50 км – 16 л
1500 км – ? л
1) 1500 : 50 = 30 (раз) – по 50 км
2) 16 ∙ 30 = 480 (л) горючего было всего
Ответ: 480 л горючего было израсходовано.
Повтори, как делить и умножать числа, оканчивающиеся нулями.
Оформляем условие в виде краткой записи.
50 км – 16 л горючего
1500 км – ? л горючего
Рассуждаем.
Нам известно, какое количество горючего требуется на 50 км пути, а путь грузовой машины – 1500 км. Вычислим, во сколько раз этот путь больше.
1500 : 50 = 30 (раз) – по 50 км.
Продолжаем рассуждение.
На 50 км пути требуется 16 л горючего, а путь, пройденный грузовой машиной, в 30 раз больше. Вычислим, сколько горючего было израсходовано.
16 ∙ 30 = 480 (л) – горючего израсходовано.
Записываем ответ.
Ответ: 480 л горючего было израсходовано.
Номер 25.
Площадь участка прямоугольной формы 3440 м2, его ширина 40 м. Найди длину участка. Составь и реши обратные задачи.
Ответ:S = 3440 м2 a = 40 м b = ? м S = a ∙ b b = S : а

Ответ: 86 м длина участка.
Обратная задача 1:
Площадь участка прямоугольной формы 3440 м2, а его длина 86 м. Найди ширину участка.

Ответ: 40 м ширина участка.
Обратная задача 2:
Длина участка прямоугольной формы 86 м, его ширина 40 м. Найди площадь участка.

Ответ: 3440 м2 площадь участка.
1) Площадь фигуры – часть плоскости, занятая фигурой.
2) Площадь прямоугольника – произведение длин его сторон.
Шаг 1.
Оформляем краткую запись.
Площадь – 3440 м2
Ширина – 40 м
Длина – ? м
Рассуждаем.
Чтобы найти длину участка, нужно площадь разделить на ширину.
3440 : 40 = 86 (м) – длина участка.
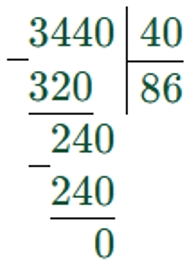
Записываем ответ.
Ответ: 86 м длина участка.
Шаг 1.
Составляем задачу обратную данной.
Площадь участка прямоугольной формы 3440 м2, а его длина 86 м. Найди ширину участка.
Оформляем краткую запись.
Площадь – 3440 м2
Длина – 86 м
Ширина – ? м
Рассуждаем.
Чтобы найти ширину участка, нужно площадь разделить на длину.
3440 : 86 = 40 (м) – ширина участка.
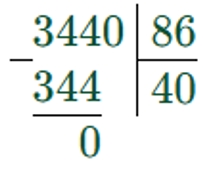
Записываем ответ.
Ответ: 40 м ширина участка.
Шаг 1.
Составляем задачу обратную данной.
Длина участка прямоугольной формы 86 м, его ширина 40 м. Найди площадь участка.
Оформляем краткую запись.
Длина – 86 м
Ширина – 40
Площадь – ? м2
Рассуждаем.
Чтобы найти площадь участка, нужно его длину умножить на ширину.
86 ∙ 40 = 3440 (м2) – площадь участка.
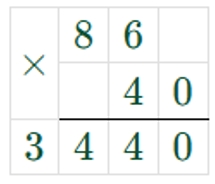
Записываем ответ.
Ответ: 3440 м2 площадь участка.
Номер 26.
В классе 20 парт. Длина крышки парты 110 см, ширина 50 см. Сколько нужно краски, чтобы покрасить крышки парт, если на 1 м² требуется 100 г краски?
Ответ:а = 110 см b = 50 см S = ? м2

1) 110 ∙ 50 = 5500 (см2) – площадь крышки парты.
2) 5500 ∙ 20 = 110000 (см2) – площадь всех крышек.
110000 см2 = 11 м2
3) 100 ∙ 11 = 1100 (г) – краски нужно для покраски парт
1100 г = 1 кг 100 г.
Ответ: 1 кг 100 г краски нужно, чтобы покрасить крышки парт.
1) Повтори, как находить площадь прямоугольника.
2) Повтори, как умножать числа, оканчивающиеся нулями.
Оформляем краткую запись.
Всего – 20 парт
Длина – 110 см
Ширина – 50 см
1 м2 – 100 г краски
Сколько всего нужно краски?
Рассуждаем.
Крышка парты – прямоугольник. Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.
110 ∙ 50 = 5500 (см2) – площадь крышки парты.
Продолжаем рассуждение.
Площадь крышки одной парты – 5500 см2. Вычислим площадь крышек 20 таких парт.
5500 ∙ 20 = 110000 (см2) = 11 (м2) – площадь крышек всех парт.
Продолжаем рассуждение.
Нужно покрыть краской 11 м2. На 1 м2 требуется 100 г краски. Узнаем, сколько граммов краски потребуется.
100 ∙ 11 = 1100 (г) = 1 (кг) 100 (г) – краски потребуется.
Записываем ответ.
Ответ: 1 кг 100 г краски нужно, чтобы покрасить крышки парт.
Номер 27.
В трёх вагонах поезда едут 100 пассажиров. В первом и втором вагонах вместе 66 пассажиров, а во втором и третьем вагонах вместе 69 пассажиров. Сколько пассажиров в каждом вагоне?
Ответ:
1) 100 − 66 = 34 (п.) – в третьем вагоне.
2) 69 − 34 = 35 (п.) – во втором вагоне.
3) 100 − 69 = 31 (п.) – в первом вагоне.
Ответ: 31 пассажир всего в первом вагоне, 35 пассажиров всего во втором вагоне, 34 пассажира всего в третьем вагоне.
Повтори способы оформления краткой записи к задаче.
Оформляем условие в виде краткой записи.
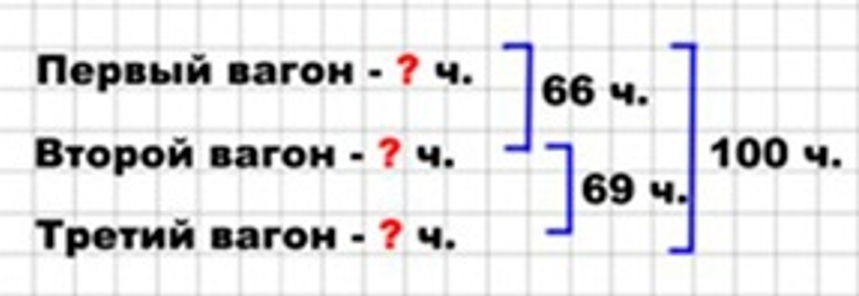
Рассуждаем.
Узнаем, сколько пассажиров едут в третьем вагоне, для этого из всего количества пассажиров вычтем количество, ехавших в первом и втором вагонах.
100 − 66 = 34 (п.) – в третьем вагоне.
Продолжаем рассуждение.
Узнаем, сколько пассажиров едут во втором вагоне, для этого из количества пассажиров, которые едут во втором и третьем вагонах, вычтем количество, ехавших в третьем вагоне.
69 − 34 = 35 (п.) – во втором вагоне.
Продолжаем рассуждение.
Узнаем, сколько пассажиров едут в первом вагоне, для этого из всего количества пассажиров вычтем количество, ехавших во втором и третьем вагонах.
100 − 69 = 31 (п.) – в первом вагоне.
Записываем ответ.
Ответ: 31 пассажир в первом вагоне, 35 пассажиров во втором вагоне, 34 пассажира в третьем вагоне.
Номер 28.
Пройдя 2 м, девочка сделала 6 шагов. Сколько таких же шагов она сделает, пройдя 10 м? 100 м?
Ответ:
1) 6 : 2 = 3 (шага) – делает девочка, пройдя 1 метр.
2) 3 ∙ 10 = 30 (шагов) – сделает девочка, пройдя 10 метров.
3) 3 ∙ 100 = 300 (шагов) – сделает девочка, пройдя 100 метров.
Ответ: 30 шагов всего сделает девочка, пройдя 1- метров и 300 шагов всего сделает девочка, пройдёт 100 метров.
Повтори единицу длины – метр.
Оформляем краткую запись.
2 м – 6 шагов
10 м – ? шагов
100 м – ? шагов
Рассуждаем.
Чтобы узнать, сколько шагов делает девочка, пройдя 1 метр, нужно количество шагов, которые она делает, пройдя 2 метра разделить на 2.
6 : 2 = 3 (шага) – делает девочка, пройдя 1 метр.
Продолжаем рассуждение.
Узнаем, сколько шагов сделает девочка, пройдя 10 метров.
3 ∙ 10 = 30 (шагов) – сделает девочка, пройдя 10 метров.
Продолжаем рассуждение.
Узнаем, сколько шагов сделает девочка, пройдя 100 метров.
3 ∙ 100 = 300 (шагов) – сделает девочка, пройдя 100 метров.
Записываем ответ.
Ответ: 30 шагов сделает девочка, пройдя 10 метров, 300 шагов сделает девочка, пройдя 100 метров.
Номер 29.
От какого предмета, мяча или кубика, может быть такая тень?

Такая тень может быть от кубика.
Повтори материал о шаре и кубе.
Рассуждаем.
Рассмотрим рисунок.

Каждая сторона тени имеет одинаковую длину 4 клетки, то есть форма тени квадратная.
Продолжаем рассуждения.
Мяч имеет форму шара, а его тень имеет форму круга.
У кубика все грани равны, то есть все грани – квадраты.
Таким образом, тень может быть от кубика.
Номер 1.
Объясни на примере, как можно разделить число на произведение.
Ответ:40 : (2 · 4) = 40 : 8 = 5
Чтобы разделить число на произведение, можно вычислить произведение и разделить на него число.
40 : (2 · 4) = (40 : 2) : 4 = 20 : 4 = 5
Чтобы разделить число на произведение, можно разделить это число на первый сомножитель, а полученный результат разделить на второй сомножитель.
40 : (2 · 4) = (40 : 4) : 2 = 10 : 2 = 5
Чтобы разделить число на произведение, можно разделить это число на второй сомножитель, а полученный результат разделить на первый сомножитель.
1) Повтори, как разделить число на произведение.
2) Можно составить любой пример.
Составим пример.
40 : (2 ∙ 4) = 40 : 8 = 5
Чтобы разделить число на произведение, можно вычислить произведение и разделить на него число.
40 : (2 ∙ 4) = (40 : 2) : 4 = 20 : 4 = 5
Чтобы разделить число на произведение, можно разделить это число на первый сомножитель, а полученный результат разделить на второй сомножитель.
40 : (2 ∙ 4) = (40 : 4) : 2 = 10 : 2 = 5
Чтобы разделить число на произведение, можно разделить это число на второй сомножитель, а полученный результат разделить на первый сомножитель.
Оформляем задание в тетрадь.
40 : (2 ∙ 4) = 40 : 8 = 5
40 : (2 ∙ 4) = (40 : 2) : 4 = 20 : 4 = 5
40 : (2 ∙ 4) = (40 : 4) : 2 = 10 : 2 = 5
Номер 2.
Составь пример, в котором нужно разделить на число, оканчивающееся нулём. Реши его с объяснением.
Ответ:8640 : 30 = 288

Первое неполное делимое – 86 сотен. В записи частного будет 3 цифры.
Делим 86 на 30, для этого 8 делим на 3, получаем 2 – столько сотен будет в частном.
30 · 2 = 60 – столько сотен разделили
86 – 60 = 26 – столько сотен осталось разделить
26 < 30
Второе неполное делимое – 264 десятка.
Делим 264 на 30, для этого 26 делим на 3, получаем 8 – столько десятков будет в частном.
30 · 8 = 240 – столько десятков разделили
264 – 240 = 24 – столько десятков осталось разделить
24 < 30
Третье неполное делимое – 240 единиц.
Делим 240 на 30, для этого 24 делим на 3, получаем 8 – столько единиц будет в частном.
30 · 8 = 240 – разделили все единицы.
1) Повтори, как разделить на число, оканчивающееся нулём.
2) Можно составить любой пример.
Составим пример.
8640 : 30 = 288
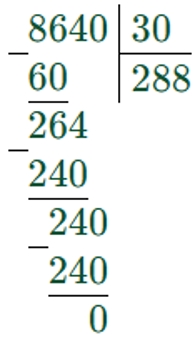
Первое неполное делимое – 86 сотен. В записи частного будет 3 цифры.
Делим 86 на 30, для этого 8 делим на 3, получаем 2 – столько сотен будет в частном.
30 ∙ 2 = 60 – столько сотен разделили
86 – 60 = 26 – столько сотен осталось разделить
26 < 30
Второе неполное делимое – 264 десятка.
Делим 264 на 30, для этого 26 делим на 3, получаем 8 – столько десятков будет в частном.
30 ∙ 8 = 240 – столько десятков разделили
264 – 240 = 24 – столько десятков осталось разделить
24 < 30
Третье неполное делимое – 240 единиц.
Делим 240 на 30, для этого 24 делим на 3, получаем 8 – столько единиц будет в частном.
30 ∙ 8 = 240 – разделили все единицы.
Оформляем задание в тетрадь.
8640 : 30 = 288
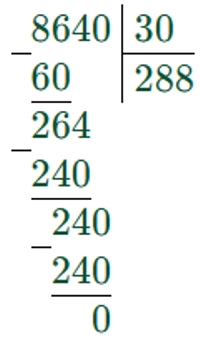
Задание на полях страницы
Магический квадрат


Проверка: 31 + 36 + 29 = 60 + 36 = 96 30 + 32 + 34 = 62 + 34 = 96 35 + 28 + 33 = 35 + 61 = 96 31 + 30 + 35 = 61 + 35 = 96 36 + 32 + 28 = 36 + 60 = 96 29 + 34 + 33 = 29 + 67 = 96 31 + 32 + 33 = 63 + 33 = 96 29 + 34 + 33 = 63 + 33 = 96
Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Рассуждаем.
Чтобы узнать, какая сумма должна быть на каждой линии, сложим имеющиеся числа в третьей строке.
35 + 28 + 33 = 96
Рассмотрим первый столбец.
31 + + 35 = 96
В столбце не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
96 – (31 + 35) = 96 – 66 = 30
30 – недостающее число в первом столбце.
Продолжаем рассуждения.
Рассмотрим первую диагональ.
31 + + 33 = 96
В диагонали не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
96 – (31 + 33) = 96 – 64 = 32
32 – недостающее число в диагонали.
Продолжаем рассуждения.
Рассмотрим вторую строку.
30 + 32 + = 96
В строчке не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
96 – (30 + 32) = 96 – 62 = 34
34 – недостающее число во второй строке.
Продолжаем рассуждения.
Рассмотрим второй столбец.
+ 32 + 28 = 96
В столбце не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
96 – (32 + 28) = 96 – 60 = 36
36 – недостающее число во втором столбце.
Продолжаем рассуждения.
Рассмотрим третий столбец.
+ 34 + 33 = 120
В столбце не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
96 – (34 + 33) = 96 – 67 = 29
29 – недостающее число в первом столбце.
Запишем недостающие числа в квадрат.
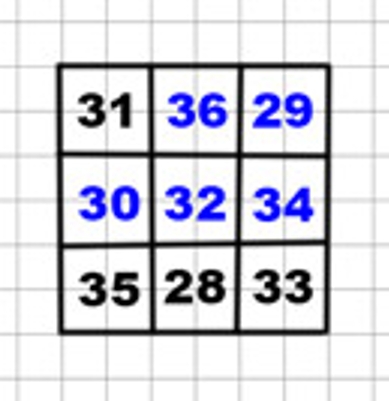
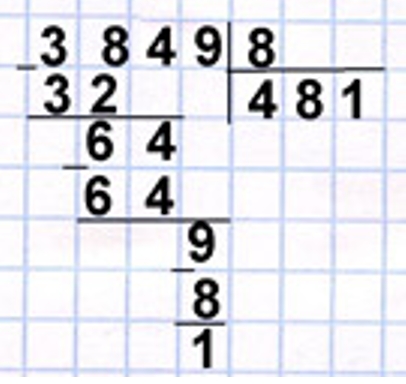
Ребус


Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.
Рассмотрим ребус.
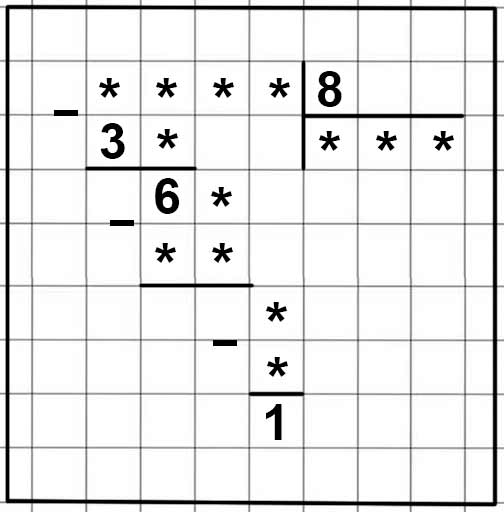
Разделили четырёхзначное число на однозначное, и получили трёхзначное число.
Рассуждаем.
Рассмотрим сотни.
Число 3∗ делится нацело на 8, значит это число – 32.
После деления первого неполного делимого получился остаток 6, значит
32 + 6 = 38 – первое неполное делимое.
В делимом 3 тысячи, 8 сотен.
32 : 8 = 4 – сотни в частном.
Рассмотрим десятки.
Так как после деления второго неполного делимого нет остатока, значит число 6∗ делится нацело на 8, значит это число – 64.
В делимом 4 десятка.
64 : 8 = 8 – десятков в частном.
Рассмотрим единицы.
Однозначное число, которое делится нацело на 8 – это число 8.
Так как третье неполное делимое – однозначное число и после его деления получился остаток 1, значит
8 + 1 = 9 – третье неполное делимое.
В делимом 9 единиц.
8 : 8 = 1 – единица в частном.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.