Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 37

Учебник 2 часть. Математика 4 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 2.
Год: 2020-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличается задание? Переключите год учебника.

2020 2024

Математика 4 класс Моро 2 часть страница 37

Номер 22.

1) От двух противоположных берегов пруда навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл до встречи со скоростью 8 м/мин, второй – со скоростью 12 м/мин. Найди ширину пруда.
2) Измени задачу, чтобы она решалась так: 200 : 10 − 8 = 12. Ответ: 12 м/мин.

Ответ:

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 22

Задача 1: 1) 8 + 12 = 20 (м/мин) – скорость сближения. 2) 20 ∙ 10 = 200 (м)
Выражение: (12 + 8) ∙ 10 = 200 (м) – ширина пруда
Ответ: 200 м ширина пруда.
Задача 2: От двух берегов пруда, ширина которого 200 м, навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл со скоростью 8 м/мин. Найди скорость второго пловца.

Подсказка:

S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.

Шаг 1.
Оформляем условие в виде схематического чертежа.

Шаг 2.
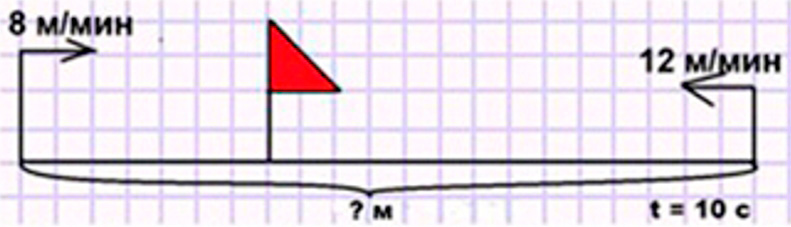
Рассуждаем.

Найдем скорость сближения пловцов. Для этого сложим скорости каждого из них вместе.
1) 8 + 12 = 20 (м/мин) – скорость сближения.

Шаг 3.
Продолжаем рассуждение.

Чтобы найти ширину пруда, нужно скорость сближения умножить на время в пути.
2) 20 ∙ 10 = 200 (м)

Шаг 4.
Записываем ответ.

Ответ: 200 м ширина пруда.
Решение выражением: (12 + 8) ∙ 10 = 200 (м)

Шаг 5.
Изменим условие задачи по заданному выражению.

От двух берегов пруда, ширина которого 200 м, навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл со скоростью 8 м/мин. Найди скорость второго пловца.

Номер 23.

Составь задачу по чертежу и реши её.

Ответ:

Из двух городов, расстояние между которыми 1200 км, вышли одновременно навстречу друг другу два поезда и встретились через 6 ч. Первый поезд шел со скоростью 98 км/ч. С какой скоростью шел второй поезд?

1-й способ решения:

1) 98 ∙ 6 = 588 (км) – проехал первый поезд. 2) 1200 − 588 = 612 (км) – проехал второй поезд. 3) 612 : 6 = 102 (км/ч)

2-й способ решения:

1) 1200 : 6 = 200 (км/ч) – скорость сближения. 2) 200 – 98 = 102 (км/ч) – скорость второго поезда

Ответ: 102 км/ч скорость второго поезда.

Подсказка:

Шаг 1.
Рассмотрим схематический чертеж к задаче из учебника.

Шаг 2.
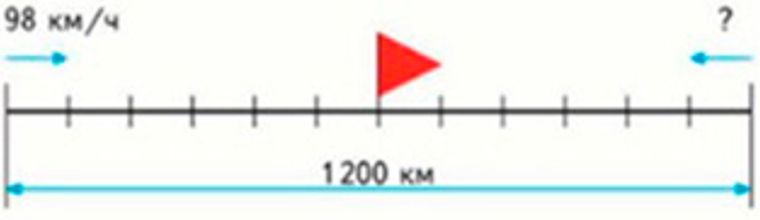
Составляем условие задачи.

Шаг 3.
Рассуждаем.

Найдем скорость сближения поездов, для этого расстояние разделим на время в пути.
1) 1200 : 6 = 200 (км/ч) – скорость сближения.

Шаг 4.
Продолжаем рассуждение.

Чтобы узнать, с какой скорость шел второй поезд, нужно из скорости сближения вычесть скорость первого поезда.
2) 200 – 98 = 102 (км/ч)

Шаг 5.
Записываем ответ.

Ответ: 102 км/ч скорость второго поезда.

Номер 24.

Грузовая машина прошла 1500 км. Сколько горючего было израсходовано, если на каждые 50 км пути требуется 16 л горючего?

Ответ:

50 км – 16 л 1500 км – ? л
1) 1500 : 50 = 30 (раз) – по 50 км 2) 16 ∙ 30 = 480 (л) – горючего израсходовано
Ответ: 480 л горючего было израсходовано.

Подсказка:

Повтори единицу длины – километр и единицу объёма – литр.

Шаг 1.
Оформляем условие в виде краткой записи.

50 км – 16 л
1500 км – ? л

Шаг 2.
Рассуждаем.

Нам известно, какое количество горючего требуется на 50 км пути, а путь грузовой машины – 1500 км. Вычислим, во сколько раз этот путь больше.
1) 1500 : 50 = 30 (раз) – по 50 км

Шаг 3.
Продолжаем рассуждение.

На 50 км пути требуется 16 л горючего, а путь, пройденный грузовой машиной, в 30 раз больше. Вычислим, сколько горючего было израсходовано.
2) 16 ∙ 30 = 480 (л)

Шаг 4.
Записываем ответ.

Ответ: 480 л горючего было израсходовано.

Номер 25.

Площадь участка прямоугольной формы 3440 м², его ширина 40 м. Найди длину участка. Составь и реши обратные задачи.

Ответ:

S = 3440 м² a = 40 м b = ? м S = a ∙ b b = S : а

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 25

Ответ: 86 м длина участка.
Обратная задача 1: Площадь участка прямоугольной формы 3440 м², а его длина 86 м. Найди ширину участка.

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 25-1

Ответ: 40 м ширина участка.
Обратная задача 2: Длина участка прямоугольной формы 86 м, его ширина 40 м. Найди площадь участка.

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 25-2

Ответ: 3440 м² площадь участка.

Подсказка:

Площадь фигуры – часть плоскости, занятая фигурой. Площадь может измеряться в единицах измерения: мм², см², дм², м², км² и др.
Площадь прямоугольника – произведение длин его сторон. Вычисляется по формуле: а ∙ в, где а и в – стороны прямоугольника.

Данная задача.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Чтобы найти длину участка, нужно площадь разделить на ширину.
3 440 : 40 = 86 (м)

Шаг 3.
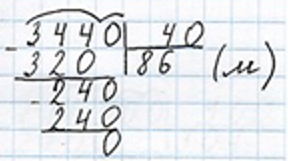
Записываем ответ.

Ответ: 86 метров длина участка.

Обратная задача 1.

Шаг 1.
Составляем первую задачу обратную данной.

Площадь участка прямоугольной формы 3440 м², а его длина 86 м. Найди ширину участка.

Шаг 2.
Оформляем условие в виде таблицы.

Шаг 3.
Рассуждаем.

Чтобы найти ширину участка, нужно площадь разделить на длину.
3 440 : 86 = 40 (м)

Шаг 4.
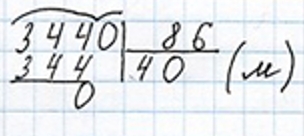
Записываем ответ.

Ответ: 40 метров ширина участка.

Обратная задача 2.

Шаг 1.
Составляем вторую задачу обратную данной.

Длина участка прямоугольной формы 86 м, его ширина 40 м. Найди площадь участка.

Шаг 2.
Оформляем условие в виде таблицы.

Шаг 3.
Рассуждаем.

Чтобы найти площадь участка, нужно его длину умножить на ширину.
86 ∙ 40 = 3 440 (м²)

Шаг 4.
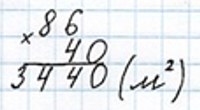
Записываем ответ.

Ответ: 3440 м² площадь участка.

Номер 26.

В классе 20 парт. Длина крышки парты 110 см, ширина 50 см. Сколько нужно краски, чтобы покрасить крышки парт, если на 1 м² требуется 100 г краски?

Ответ:

а = 110 см b = 50 см S = ? м²

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 26

1) 110 ∙ 50 = 5500 (см²) – площадь крышки парты. 2) 5500 ∙ 20 = 110000 (см²) – площадь всех крышек. 110000 см² = 11 м² 3) 100 ∙ 11 = 1100 (г) 1100 г = 1 кг 100 г.
Ответ: 1 кг 100 г краски нужно, чтобы покрасить крышки парт.

Подсказка:

Повтори, как найти площадь прямоугольника, единицы длины – метр и сантиметр, а также единицы массы – грамм и килограмм.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
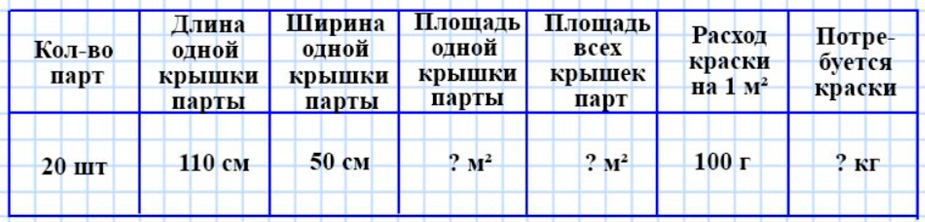
Рассуждаем.

Крышка парты – прямоугольник. Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.
1) 110 ∙ 50 = 5500 (см²) – площадь крышки парты.

Шаг 3.
Продолжаем рассуждение.

Площадь крышки 1 парты – 5500 см². Вычислим площадь 20 таких парт.
2) 5500 ∙ 20 = 110000 (см²) – площадь всех крышек.

Шаг 4.
Продолжаем рассуждение.

Нужно покрыть краской 11 м². На 1 м² требуется 100 г краски. Узнаем, сколько граммов краски потребуется.
110000 см² = 11 м²
3) 100 ∙ 11 = 1100 (г)
1100 г = 1 кг 100 г.

Шаг 5.
Записываем ответ.

Ответ: 1 кг 100 г краски нужно, чтобы покрасить крышки парт.

Номер 27.

В трёх вагонах поезда едут 100 пассажиров. В первом и втором вагонах вместе 66 пассажиров, а во втором и третьем вагонах вместе 69 пассажиров. Сколько пассажиров в каждом вагоне?

Ответ:

математика 4 класс Моро, Бантова - 2 часть страница 37, номер 27

1) 100 − 66 = 34 (п.) – в третьем вагоне. 2) 69 − 34 = 35 (п.) – во втором вагоне. 3) 100 − 69 = 31 (п.) – в первом вагоне.
Проверка: 34 + 35 + 31 = 100 Ответ: 31 пассажир всего в первом вагоне, 35 пассажиров во втором вагоне, 34 пассажира в третьем вагоне.

Подсказка:

Повтори способы оформления краткой записи к задаче.

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
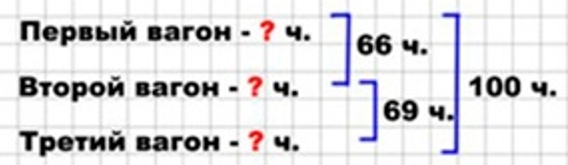
Рассуждаем.

Узнаем, сколько пассажиров едут в третьем вагоне, для этого из всего количества пассажиров вычтем количество, ехавших в первом и втором вагонах.
1) 100 − 66 = 34 (п.) – в третьем вагоне.

Шаг 3.
Продолжаем рассуждение.

Узнаем, сколько пассажиров едут во втором вагоне, для этого из количества пассажиров, которые едут во втором и третьем вагонах, вычтем количество, ехавших в третьем вагоне.
2) 69 − 34 = 35 (п.) – во втором вагоне.

Шаг 4.
Продолжаем рассуждение.

Узнаем, сколько пассажиров едут в первом вагоне, для этого из всего количества пассажиров вычтем количество, ехавших во втором и третьем вагонах.
3) 100 − 69 = 31 (п.) – в первом вагоне.

Шаг 5.
Записываем ответ.

Ответ: 31 пассажир, 35 пассажиров, 34 пассажира.

Номер 28.

Пройдя 2 м, девочка сделала 6 шагов. Сколько таких же шагов она сделает, пройдя 10 м? 100 м?

Ответ:

2 м – 6 шагов 10 м – ? шагов 100 м – ? шагов
1) 6 : 2 = 3 (шага) – делает девочка, пройдя 1 метр. 2) 3 ∙ 10 = 30 (шагов) – сделает девочка, пройдя 10 метров. 3) 3 ∙ 100 = 300 (шагов) – сделает девочка, пройдя 100 метров.
Ответ: 30 шагов сделает девочка, пройдя 10 метров; и 300 шагов сделает девочка, пройдя 100 метров.

Подсказка:

Повтори единицу длины – метр.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Чтобы узнать, сколько шагов делает девочка, пройдя 1 метр, нужно количество шагов, которые она делает, пройдя 2 метра разделить на 2.
1) 6 : 2 = 3 (шага) – делает девочка, пройдя 1 метр.

Шаг 3.
Продолжаем рассуждение.

Узнаем, сколько шагов сделает девочка, пройдя 10 метров.
2) 3 ∙ 10 = 30 (шагов) – сделает девочка, пройдя 10 метров.

Шаг 4.
Продолжаем рассуждение.

Узнаем, сколько шагов сделает девочка, пройдя 100 метров.
3) 3 ∙ 100 = 300 (шагов) – сделает девочка, пройдя 100 метров.

Шаг 5.
Записываем ответ.

Ответ: 30 шагов и 300 шагов.

Номер 1.

Объясни на примере, как можно разделить число на произведение.

Ответ:

40 : (2 ∙ 4) = (40 : 4) : 2 = 10 : 2 = 5 Число на произведение можно разделить так: Раскрыть скобки и теперь каждый из множителей становится делителем. Удобным способом группируем исходное частное и один из делителей. Выполняем деление и делим полученное число на оставшийся из двух множителей новый делитель.

Подсказка:

Повтори, как делить на круглые числа. Ты можешь составить другой пример.

Шаг 1.
Составим пример и решим его с объяснением.

40 : (2 ∙ 4) = (40 : 4) : 2 = 10 : 2 = 5
Число на произведение можно разделить так:
Раскрыть скобки и теперь каждый из множителей становится делителем. Удобным способом группируем исходное частное и один из делителей. Выполняем деление и делим полученное число на оставшийся из двух множителей новый делитель.

Шаг 2.
Оформляем задание в тетрадь.

Номер 2.

Составь пример, в котором нужно разделить на число, оканчивающееся нулём. Реши его с объяснением.

Ответ:

6412 : 10 = 641 (ост. 2) Попробуем по 6. 64 минус 60 равно 4. Сносим 1. 41 разделить на 10, попробуем по 4. 41 минус сорок, будет 1. Сносим 2. Попробуем по 1, тогда 12 минус 10 будет 2 и это остаток. Читаем ответ: 641 - неполное частное, а 2 - остаток.

Подсказка:

Повтори, как делить на круглые числа. Ты можешь составить другой пример.

Шаг 1.
Составим пример и решим его с объяснением.

6412 : 10 = 641 (ост. 2)
1) Попробуем по 6.
2) 64 минус 60 равно 4.
3) Сносим 1.
4) 41 разделить на 10, попробуем по 4.
5) 41 минус сорок, будет 1.
6) Сносим 2.
7) Попробуем по 1, тогда 12 минус 10 будет 2 и это остаток.
8) Читаем ответ: 641 – неполное частное, а 2 – остаток.

Шаг 2.
Оформляем задание в тетрадь.

Задание на полях страницы

Магический квадрат

Ответ:

Проверка: 31 + 36 + 29 = 36 + 60 = 96 30 + 32 + 34 = 30 + 66 = 96 35 + 28 + 33 = 28 + 68 = 96 31 + 30 + 35 = 61 + 35 = 96 36 + 32 + 28 = 36 + 60 = 96 29 + 34 + 33 = 29 + 67 = 96 31 + 32 + 33 = 63 + 33 = 96 35 + 32 + 29 = 35 + 61 = 96

Подсказка:

Магический квадрат – таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.

Шаг 1.
Выполняем вычисления.

35 + 28 + 33 = 96
96 – (31 + 35) = 30
96 – (31 + 33) = 32
96 – (30 + 32) = 34
96 – (28 + 32) = 36
96 – (31 + 36) = 29

Шаг 2.
Заполняем магический квадрат.

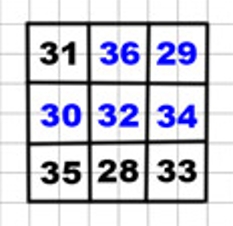
Ребус

Ответ:

Подсказка:

Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.

Шаг 1.
Рассмотрим ребус.

Шаг 2.
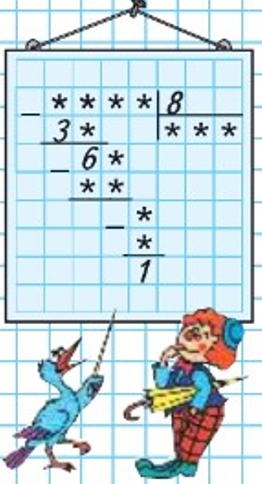
Разгадаем ребус.

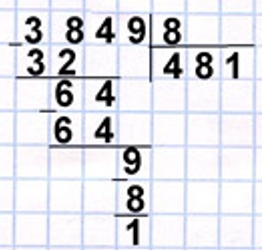
Какое число с 3 десятками делится на 8? Эточисло 32. После деления первого неполного делимого в остатке получилось 6.
32 + 6 = 38.
38 : 8 = 4 (ост. 6)
Какое число с 6 десятками делится на 8 без остатка? Это число 64.
64 : 8 = 8.
Какое однозначное число делится на 8? Это число 8. После деления третьего неполного делимого в остатке получилось 1.
8 + 1 = 9.
9 : 8 = 1 (ост. 1)

Шаг 3.
Оформим задание в тетрадь.

Математика 4 класс Моро 2 часть страница 37. 2024 год

Что узнали. Чему научились

Номер 1.

Ответ:

84 ∙ 10 − 40 = 840 − 40 = 800 78 ∙ 10 − 700 = 780 − 700 = 80
10 ∙ (920 − 20) = 10 ∙ 900 = 9000 8 ∙ (720 − 700) = 8 ∙ 20 = 160
184 ∙ 100 − 300 = 18400 − 300 = 18100 100 ∙ 391 − 3000 = 39100 − 3000 = 36100

Номер 2.

Ответ:

Номер 3.

Ответ:

Номер 4.

Выполни деление с остатком.

Ответ:

Математика 4 класс Моро, Бантова - 2 часть страница 37, номер 4. Год 2024.

Номер 5.

Вычисли удобным способом.

Ответ:

45 ∙ (2 ∙ 7) = (45 ∙ 2) ∙ 7 = 90 ∙ 7 = 630 720 : (9 ∙ 2) = (720 : 9) : 2 = 80 : 2 = 40 67 ∙ (4 ∙ 25) = 67 ∙ 100 = 6700 17 ∙ 2 ∙ 8 ∙ 125 = 34 ∙ 1000 = 34000

Номер 6.

Ответ: