Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 99

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задания повышенного уровня сложности
Номер 1.
Определи, по какому правилу составлена последовательность чисел, и запиши пропущенные в ней числа:
13546, 14547, 15548, ..., ..., ..., 19552.
Ответ:К предыдущему числу прибавляется 1001: 13546, 14547, 15548, 16549, 17550, 18551, 19552.
Для того, чтобы понять, какое число будет следующим, необходимо проанализировать ряд – из каких компонентов он состоит, какие они: двузначные, однозначные, четные или нечетные.
Выполняем вычисления.
13 546 + 1 001 = 14 547
14 547 + 1 001 = 15 548
15 548 + 1 001 = 16 549
16 549 + 1 001 = 17 550
17 550 + 1 001 = 18 551
18 551 + 1 001 = 19 552
Оформляем задание в тетрадь.
К предыдущему числу прибавляется 1001:
13546, 14547, 15548, 16549, 17551, 18551, 19552.
Номер 2.
Какие однозначные числа можно записать в окошко, чтобы при делении суммы 30 + ☐ на 4 получался остаток? Запиши эти числа в порядке их уменьшения.
Ответ:30 + … 9, 8, 7, 5, 4, 3, 1, 0
Помни о названии компонентов действия деления: делимое, делитель, значение частного.
Однозначные числа – числа, в записи которых используется один знак.
Выполняем вычисления.
Чтобы при делении числа на 4 получался остаток, это число не должно быть результатом таблицы умножения 4. Числа четвертого десятка кратные 4 образовывать нельзя.
Это числа: 32, 36, потому что 32 : 4 = 8, 36 : 4 = 9
Значит, все оставшиеся числа четвертого десятка можно образовать:
31; 30 + 1 = 31; 31 : 4 = 7 (ост 3)
33; 30 + 3 = 33; 33 : 4 = 8 (ост 1)
34; 30 + 4 = 34; 34 : 4 = 8 (ост 2)
35; 30 + 5 = 35; 35 : 4 = 8 (ост 3)
37; 30 + 7 = 37; 37 : 4 = 9 (ост 1)
38; 30 + 8 = 38; 38 : 4 = 9 (ост 2)
39; 30 + 9 = 39; 39 : 4 = 9 (ост 3)
Оформляем задание в тетрадь.
30 + …
9, 8, 7, 5, 4, 3, 1, 0
Номер 3.
Запиши данные значения массы в порядке их увеличения: 8 ц, 800 г, 8 т, 80 т, 8 кг.
Ответ:800 г, 8 кг, 8 ц, 8 т, 80 т.
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек
1 час – 60 мин
1 сут – 24 час
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес
1 год – 356 сут.
Рассуждаем и выполняем вычисления.
Для того, чтобы расположить числовые значения времени в порядке их увеличения (т.е. от меньшего к большему) нужно сначала привести их к одним единицам измерения, но первоначально проанализируем все значения: 8 ц, 800 г, 8 т, 80 т, 8 кг
Значит, имеются: центнер, грамм, тонна, килограмм. Расположим их в порядке увеличения:
1 т – 1000 кг
1 ц – 100 кг
1 кг – 1000 г
Получается: грамм – килограмм – центнер – тонна
Значит, располагаю в порядке уменьшения значения: 800 г, 8 кг, 8 ц, 8 т, 80 т.
Оформляем задание в тетрадь.
800 г, 8 кг, 8 ц, 8 т, 80 т.
Номер 4.
Ответ:
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Вычитаю сотни.
7) Вычитание окончено. Читаю ответ.
Рассуждаем.
1 пример
Чтобы в единицах получился 0, нужно к 9 прибавить 1.
9 + 1 = 10 ед.
10 ед. − это 1 дес. 0 ед.
1 дес. запоминаем и прибавим к десяткам.
3 дес. + 9 дес. = 12 дес. и еще 1 дес. получим 13 дес.
13 дес. − 1 сот. и 3 дес.
1 сот. запоминаем и прибавим к сотням.
Чтобы в сотнях получилось 4, нужно к (6 + 1) прибавить 7.
7 + 8, да ещё 1, получится 16. Пишу 6 под единицами тысяч.
2 пример
10 − 5 = 5. Пишу 5 под единицами.
Из 9 брали 1 сот. при вычитании единиц. Из 8 нельзя вычесть однозначное число, чтобы в разности получилось 9. Значит, вычитали из 18 число 9.
Из 10 дес. тыс. брали 1 дес. тыс. при вычитании сотен, осталось 9 дес. тыс. Из 9 нужно вычесть 2, чтобы получилось 7.
Из 9 сот. тыс. брали 1 сот. тыс. при вычитании сотен, осталось 8 сот. тыс.
3 пример
Чтобы в единицах получилось 2, нужно 8 умножить на 4 или 9.
Предположим, что второй множитель − 4.
8 ∙ 4 = 32.
4 ∙ 4 = 16, да ещё 3 дес., которые получились при умножении единиц: 16 + 3 = 19. В десятках должно получиться 9, но там записано число − 3, значит второй множитель − 9.
8 ∙ 9 = 72.
4 ∙ 9 = 36, да ещё 7 дес., которые получились при умножении единиц:
36 + 7 = 43.
2 ∙ 9 = 18, да ещё 4 сот., которые получились при умножении десятков:
18 + 4 = 22.
6 ∙ 9 = 54, да ещё 2 ед. тыс., которые получились при умножении сотен:
54 + 2 = 56.
4 пример
Разделю 36 на 8, получится 4.
Умножу 4 на 8, получится 32.
Вычту: 36 − 32 = 4.
Разделю 41 на 8, получится 5.
Умножу 5 на 8, получится 40.
Вычту: 41 − 40 = 1.
Разделю 13 на 8, получится 1.
Умножу 1 на 8, получится 8.
Вычту: 13 − 8 = 5.
Какое двузначное число с 5 десятками делится на 8 без остатка? Это число 56.
Вставляем пропуски и оформляем задание в тетрадь.
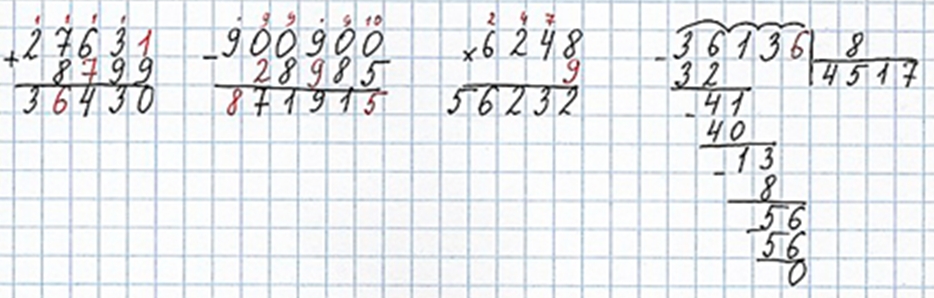
Номер 5.
Поставь скобки так, чтобы равенство стало верным.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисление значений выражения сводится к применению правил:
Правило вычитания числа из суммы: (а + в) – с = (а – с) + в
Выполняем вычисления.
(1 540 – 1 000) : 6 – 30 = 60
1) 1 540 – 1 000 = (1 000 + 540) – 1 000 = (1 000 – 1 000) + 540 = 540, по правилу вычитания числа из суммы
2) 540 : 6 = 54 дес. : 6 = 9 дес. = 90
3) 90 – 30 = 9 дес. – 3 дес. = 6 дес. = 60
Выполняем проверку.
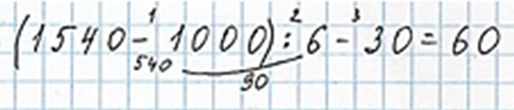
Номер 6.
На нижней полке 18 книг. Это в 3 раза больше, чем на верхней полке. Сколько книг на верхней полке?
Ответ:
18 : 3 = 6 (кн.) – на верхней полке.
Ответ: 6 книг всего стоит на верхней полке.
Условно задача в косвенной форме формулируется так: это на столько-то больше, чем то.
Задача в косвенной форме решается в зависимости от вопроса: «это на х больше», значит, решается вычитанием, а если: «это на х меньше», значит, решается сложением.
«это в 3 раза больше», значит, вычисляется делением, потому что задача в косвенной форме.
Оформляем условие в виде краткой записи.
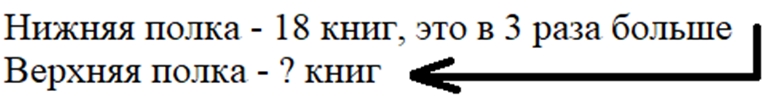
Рассуждаем.
Чтобы узнать, сколько книг на верхней полке, нужно количество книг нижней полки разделить на 3.
18 : 3 = 6 (кн.) – на верхней полке.
Записываем ответ.
Ответ: 6 книг.
Номер 7.
Для ремонта дома купили 900 мелких и 100 крупных гвоздей. Все мелкие гвозди разложили в 3 ящика поровну, а все крупные – в 2 ящика поровну. На сколько больше гвоздей в одном ящике с мелкими гвоздями, чем в одном ящике с крупными гвоздями?
Ответ:
1) 900 : 3 = 300 (шт.) – мелких в одном ящике.
2) 100 : 2 = 50 (шт.) – крупных в одном ящике.
3) 300 − 50 = 250 (шт.) – больше в ящике с мелкими гвоздями
Ответ: на 250 гвоздей больше в ящике с мелкими гвоздями, чем в одном ящике с крупными гвоздями.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения
Значение произведения : 1 множитель = 2 множитель
Значение произведения : 2 множитель = 1 множитель
Данная задача: вида «количество гвоздей в 1 коробке, количество коробок, общее количество гвоздей» характеризуется зависимостями между компонентами:
Кол-во гвоздей 1 коробки ∙ кол-во коробок = общее кол-во гвоздей
Общее кол-во гвоздей : кол-во коробок = кол-во гвоздей 1 коробки
Общее кол-во гвоздей : кол-во гвоздей 1 коробки = кол-во коробок
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько мелких гвоздей в 1 коробке, нужно общее количество гвоздей разделить на количество коробок.
1) 900 : 3 = 300 (шт.) – мелких в одном ящике.
Продолжаем рассуждение.
Чтобы узнать, сколько крупных гвоздей в 1 коробке, нужно общее количество гвоздей разделить на количество коробок.
2) 100 : 2 = 50 (шт.) – крупных в одном ящике.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Значит, из количества мелких гвоздей 1 коробки вычитаем количество крупных гвоздей 1 ящика.
3) 300 − 50 = 250 (шт.)
Записываем ответ.
Ответ: на 250 гвоздей больше в ящике с мелкими гвоздями, чем в одном ящике с крупными гвоздями.
Решение выражением: (900 : 3) – (100 : 2), где 900 : 3 – количество маленьких гвоздей 1 коробки; 100 : 2 – количество крупных гвоздей 1 ящика.
Номер 8.
Длина огорода прямоугольной формы 20 м, а ширина в 2 раза меньше.
1) Сколько метров сетки потребуется, чтобы огородить его со всех сторон?
2) Найди площадь этого огорода.
1) 20 : 2 = 10 (м) – ширина огорода.
2) (20 + 10) ∙ 2 = 60 (м) – сетки надо.
3) 20 ∙ 10 = 200 (м2) – площадь огорода.
Ответ: 60 м сетки нужно для того, чтобы огородить со всех сторон, площадь огорода составляет 200 м2.
«в 2 раза меньше», значит, вычисляется делением
Длина ломаной – сумма длин всех отрезков звеньев. Чтобы вычислить длину ломаной, нужно измерить длины всех звеньев, а полученные значения сложить. Вычисляется сложением. В независимости от того, замкнутая ломаная или нет, ее длина всегда вычисляется одинаково.
Прямоугольник – замкнутая ломаная
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Найдем ширину прямоугольника.
Для этого нужно длину огорода разделить на 2, потому что известно, что ширина в 2 раза меньше.
1) 20 : 2 = 10 (м) – ширина огорода.
Найдем периметр огорода.
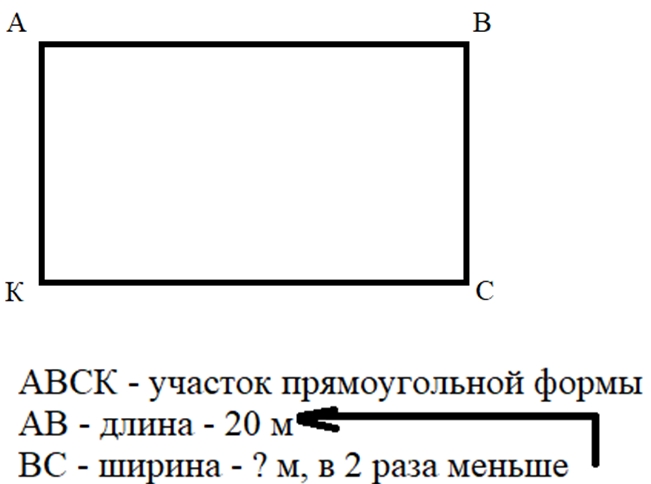
АВ = КС = 20 м
АК = ВС = 10 м
Р = (АВ + ВС) ∙ 2
Р = (20 + 10) ∙ 2 = 30 ∙ 2 = 60 м – периметр прямоугольника и длина сетки, ведь периметр фигуры – длина замкнутой ломаной
Найдем площадь огорода.
АВСК – прямоугольник
АВ = КС = 20 м
АК = ВС = 10 м
S = ? м2
S = АВ ∙ ВС
S = 20 ∙ 10 = 200 м2
Записываем ответ.
Ответ: 60 м, 200 м².
Номер 9.
Из двух квадратов с длиной стороны 2 см сложили прямоугольник. Сделай чертёж. Найди периметр и площадь этого прямоугольника.
Ответ:Периметр: (4 + 2) ∙ 2 = 12 см Площадь: 4 ∙ 2 = 8 см2

Длина ломаной – сумма длин всех отрезков звеньев. Чтобы вычислить длину ломаной, нужно измерить длины всех звеньев, а полученные значения сложить. Вычисляется сложением. В независимости от того, замкнутая ломаная или нет, ее длина всегда вычисляется одинаково.
Квадрат – замкнутая ломаная
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Рассуждаем и выполняем вычисление.

Найдем длину стороны прямоугольника.
Длина стороны квадрата – 2 см, длина стороны прямоугольника складывается из двух сторон квадрата, лежащих на одной прямой. Тогда, чтобы узнать, чему равна сторона прямоугольника, нужно сложить стороны двух квадратов.
Т.е. 2 см + 2 см = 4 см – длина стороны прямоугольника.
Найдем периметр прямоугольника.
Теперь нам известно, что длина прямоугольника – 4 см, а ширина – 2 см. Периметр – сумма длин всех сторон фигуры.
Значит, чтобы узнать, чему равен периметр прямоугольника, можно поступить 3 способами:
1 способ: сложить длины всех сторон, т.е. а + в + а + в
2 способ: сложить удвоенные длины сторон, т.е. а ∙ 2 + в ∙ 2
3 способ: сложить длины отличных друг от друга сторон, а полученную сумму удвоить, т.е. (а + в) ∙ 2
Тогда, периметр прямоугольника равен: (4 + 2) ∙ 2 = 12 см
Найдем площадь прямоугольника.
Площадь – произведение длин сторон прямоугольника. Вычисляется по формуле. Тогда, 4 см ∙ 2 см = 8 см2.
Но вычислить значение площади можно иначе, ведь площадь большой фигуры складывается из суммы площадей фигур, из которых она состоит. Тогда, можно вычислить площадь квадрата, а полученное значение удвоить, ведь квадрата два и они одинаковые.
Тогда, ( 2 ∙ 2) ∙ 2, где 2 ∙ 2 – площадь квадрата, а 2 – количество квадратов.
Запишем ответ.
Ответ: 12 см, 8 см2
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.