Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 73

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 22.
Дополни задачу недостающими данными и реши её. Из неисправного водопроводного крана в секунду капают 2 капли, а за 12 мин наполняется 1 полный стакан. Сколько литров воды может зря вылиться из такого крана в течение часа? в течение суток? (Считать в литре ☐ стаканов.)
Ответ:Считать, что в 1 литре 5 стаканов, потому что в одном стакане 200 мл.
Сколько стаканов воды выльется за 1 час?
60 : 12 = 5 (ст.) – за 1 час и это 1 л.
Значит за 1 час выливается 1 литр воды. За сутки (24 с) выльется 24 литра.
Ответ: 1 л воды можно вылить из крана в течение часа; и 24 л воды выльется из крана в течение суток.
Чтобы дополнить условие задачи, выполним реальные действия, т.е. отмерим стаканами 1 литр, чтобы понять, сколько в литре стаканов. Используем весы или специальную мерную ёмкость.
Дополняем задачу данными.
Считать, что в 1 литре 5 стаканов, потому что в одном стакане 200 мл.
Оформляем условие в виде краткой записи.

Рассуждаем.
1 час – 60 минут, значит, чтобы понять, сколько стаканов наливается за 1 час, необходимо общее количество времени разделить на время, которое тратится на 1 стакан. 60 : 12 = 5 (ст.) – набирается за 1 час.
Продолжаем рассуждение.
За 1 час выливается 5 стаканов, а мы узнали, что 5 стаканов – 1 литр. Значит, чтобы узнать, сколько воды выльется за 1 сутки, нужно кол-во воды выливающейся за 1 час умножить на количество часов.
1 · 24 = 24 (л.) – за сутки.
Записываем ответ.
Ответ: за 1 час выльется 1 литр воды, а за 24 часа – 24 литра.
Номер 23.
Какую площадь занимает картофельное поле, если одна пятая часть этой площади составляет 200 м2?
Ответ:Все поле – ? м2.
1/5 часть – 200 м2.
200 ∙ 5 = 1000 (м2).
Ответ: 1000 м2 занимает картофельное поле.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического чертежа.
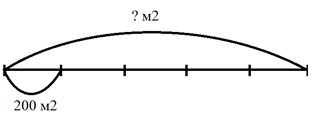
Рассуждаем.
Одна пятая часть поля – это одна часть из пяти. Эта часть равна 200 м2. Значит, чтобы узнать, чему равна общая площадь поля, нужно площадь одной части умножить на количество частей.
200 ∙ 5 = 1000 (м2)
Записываем ответ.
Ответ: 1000 м2 занимает картофельное поле.
Номер 24.
Какие числа пропущены в таблице?
Ответ:1 см2 = 100 мм2 1 м2 = 100 дм2 1 дм2 = 100 см2 1 км2 = 1000000 м2
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Выполняем вычисления.
1 см2; 1 см2 – это 100 мм2, потому что 10 мм · 10 мм = 100 мм2.
1 дм2; 1 дм2 – это 100 см2, потому что 10 см · 10 см = 100 см2.
1 м2; 1 м2 – это 100 дм2, потому что 10 дм · 10 дм = 100 дм2.
1 км2; 1 км2 – это 1 000 000 м2, потому что 1 000 м · 1 0000 м = 1 000 000 м2.
Оформляем задание в тетрадь.
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 100 дм2
1 км2 = 1000000 м2
Номер 25.
Запиши вычисления столбиком.
Ответ:45 км 530 м + 37 км 470 м = 83 км. 45 км 530 м = 45530 м. 37 км 470 м = 37470 м. 83000 м = 83 км.
24 км 040 м – 9 км 008 м = 15 км 032 м. 24 км 040 м = 24040 м. 9 км 008 м = 9008 м. 15032 м = 15 км 032 м.
32 т 820 кг − 8 т 950 кг = 23 т 870 кг. 32 т 820 кг = 32820 кг. 8 т 950 кг = 8950 кг. 23 т 870 кг = 23870 кг.
3 ч 15 мин – 45 мин = 2 ч 30 мин. 3 ч 15 мин = 195 мин. 195 мин – 45 мин = 150 мин. 150 мин = 2 ч 30 мин.

Помни о том, что могут существовать два случая сложения величин:
Простой, когда вычисления можно произвести устно: 1 ч 15 мин + 45 мин = 2 ч.
Сложный, когда необходима запись вычислений с приведением числовых значений к одним единицам измерения.
Помни о том, что числовые значения единиц можно складывать только с соответствующими им единицами, например, минуты с минутами, часы с часами.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек.
1 час – 60 мин.
1 сут – 24 час.
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес.
1 год – 356 сут.
Масса – величина, которая характеризует вес предмета, то, сколько он весит. Масса может измеряться в таких единицах измерения, как грамм, килограмм, центнер, тонна.
Помни о соотношении числовых значений единиц измерения времени:
1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.
Выполняем вычисления.
45 км 530 м + 37 км 470 м = 83 км.
45 км 530 м = 45530 м.
37 км 470 м = 37470 м.
83000 м = 83 км.

24 км 040 м – 9 км 008 м = 15 км 032 м.
24 км 040 м = 24040 м.
9 км 008 м = 9008 м.
15032 м = 15 км 032 м.

32 т 820 кг – 8 т 950 кг = 23 т 870 кг.
32 т 820 кг = 32820 кг.
8 т 950 кг = 8950 кг.
23 т 870 кг = 23870 кг.

3 ч 15 мин – 45 мин = 2 ч 30 мин.
3 ч 15 мин = 195 мин.
195 мин – 45 мин = 150 мин.
150 мин = 2 ч 30 мин.

Оформляем задание в тетрадь.

Номер 26.
Из двух одинаковых квадратов составили прямоугольник со сторонами 3 см и 1 см 5 мм. Сделай к задаче чертёж. Вырази длины сторон прямоугольника в миллиметрах и вычисли периметр этого прямоугольника и каждого квадрата.
Ответ:
3 см = 30 мм.
1 см 5 мм – 15 мм.
Периметр прямоугольника: (30 + 15) ∙ 2 = 90 (мм).
Периметр квадрата: 15 ∙ 4 = 60 (мм).
Ответ: периметр прямоугольника – 9 см, периметр каждого квадрата – 6 см.
Периметр фигуры – сумма длин всех ее сторон. Чтобы вычислить периметр прямоугольника, нужно измерить длины всех сторон, а полученные значения сложить.
Сделать это можно тремя способами, ведь у прямоугольника противоположные стороны равны:
1 способ: а + в + а + в.
2 способ: а · 2 + в · 2.
3 способ: (а + в) · 2.
Делаем чертеж к задаче.

Выражаем длины сторон в миллиметрах.
3 см = 30 мм.
1 см 5 мм = 15 мм.
Вычисляем периметр прямоугольника.
АВСК – прямоугольник.
АВ = КС = 3 см.
АК = ВС = 1 см 5 мм.
Р = (АВ + ВС) · 2.
Р = (30 + 15) ∙ 2 = 90 (мм).
90 мм = 9 см.
Вычисляем периметр каждого квадрата.
Чтобы узнать, чему равен периметр квадрата, нужно длину одной стороны умножить на 4.
Р = 15 ∙ 4 = 60 (мм).
60 мм = 6 см.
Записываем ответ.
Ответ: периметр прямоугольника – 9 см, периметр каждого квадрата – 6 см.
Номер 27.
Начерти такие фигуры в тетради. В фигуре 1 найди одну девятую долю и закрась четыре таких доли, а в фигуре 2 закрась семь шестнадцатых долей. Найди площадь незакрашенной части фигуры 1.
Ответ:
3 ∙ 3 = 9 см2.
9 − 4 = 5 см2.
Ответ: 5 см2 площадь незакрашенной части фигуры 1.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Начертим фигуры в тетрадь и закрасим их, исходя из данных задачи.

Рассуждаем.
Вычисляем площадь квадрата. Он складывается из 9 квадратов по 1 см2 каждый.
1 см2 · 9 = 9 (см2) – площадь всей фигуры.
Продолжаем рассуждение.
Чтобы узнать, чему равна площадь не закрашенной части, нужно из общей площади фигуры вычесть площадь закрашенной части. Вычисляется вычитанием. знак минус.
9 см2 – 4 см2 = 5 (см2).
Записываем ответ.
Ответ: 5 см2 площадь не закрашенной части фигуры 1.
Номер 1.
Как называются числа и соответствующие выражения при сложении? вычитании?
Ответ:При сложении: первое слагаемое, второе слагаемое, сумма. При вычитании: уменьшаемое, вычитаемое, разность.
Вспомни названия компонентов действия сложения и вычитания, а также зависимость между компонентами и результатом действия сложения, вычитания.
Арифметическое действие сложение.
Сложение – т.е. объединение частей в целое, значит, слагаемые – это части, которые складывают. Поэтому названия первого и второго слагаемых происходят от слова слагать, т.е. складывать, объединять.
Результат сложения – сумма. Это слово намного древнее, ведь в старые времена, суммой называли кошель с деньгами, т.е. целое, куда все части складывали.
Так и повелось, что компоненты сложения до сих пор называются: слагаемые и сумма.
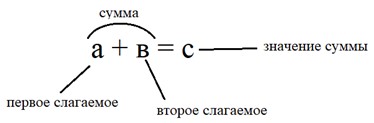
Арифметическое действие вычитание.
Само слово вычитать, значит, уменьшать, убирать, сокращать. Поэтому первый компонент действия – уменьшаемое, значит, что это число, которое уменьшают.
Если число уменьшают, то из него что-то вычитают, т.е. вычитаемое – число, которое вычитают; часть, на которую вычитаемое становится меньше.
И наконец, разность – очень похоже на слово разница. От него название компонента и произошло, ведь если от целого отнять часть, то и получится эта часть, что и представляет собой разницу межу большим числом, которое уменьшают и числом, которое вычитают.
Таким образом, названия компонентов: уменьшаемое, вычитаемое и разность.
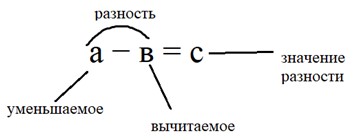
Номер 2.
Какие свойства сложения ты знаешь?
Ответ:• Переместительное свойство сложения – от перестановки мест слагаемых значение суммы не меняется a + b = b + a
• Сочетательное свойство сложения – можно складывать слагаемые в любом порядке. Значение суммы от этого не поменяется (Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.) (a + b) + c = a + (b + c)
• Свойство нуля при сложении – если к числу прибавить 0, получится тоже самое число. a + 0 = 0 + a = a
Разные арифметические действия основывают на разных арифметических действиях, но есть и общие, характерные для всех арифметических действий.
Например, переместительное свойство, сочетательное свойство – они характерны для разных арифметических действий.
А такие свойства, как:
Правило прибавления числа к нулю, 0 + а.
Правило прибавления нуля к числу, а + 0.
Правило умножения числа на 1, а · 1.
Правило умножения числа на 0, а · 0.
Правило деления числа на 1, а : 1.
Правило деления 0 на число, 0 : а.
Переместительное свойство.
Переместительное свойство сложения – от перестановки мест слагаемых значение суммы не меняется.
a + b = b + a.
Сочетательное свойство.
Сочетательное свойство сложения – можно складывать слагаемые в любом порядке. Значение суммы от этого не поменяется (Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.)
(a + b) + c = a + (b + c).
Свойство нуля при сложении.
Свойство нуля при сложении – если к числу прибавить 0, получится тоже самое число.
a + 0 = 0 + a = a.
Номер 3.
Чему равна сумма двух слагаемых, если одно из них равно нулю? разность, если вычитаемое равно нулю?
Ответ:Сумма равна слагаемому неравному нулю. Разность равна уменьшаемому.
Помни о названии компонентов действия сложения и вычитания:
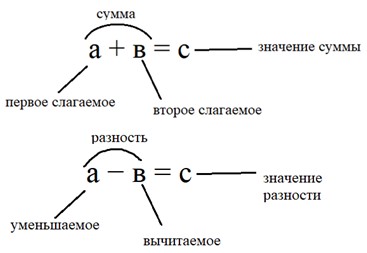
А также – зависимости между компонентами и результатом действий сложения и вычитания.
1 слагаемое + 2 слагаемое = значение суммы.
Значение суммы – 1 слагаемое = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Сумма двух слагаемых, одно из которых равно нулю.
а + 0 = а, значит, сумма двух слагаемых, одно из которых равно нулю, равна другому слагаемому.
Разность, если вычитаемое равно нулю.
а – 0 = а, значит, разность, если вычитаемое равно нулю, равно уменьшаемому.
Номер 4.
Что получится, если из суммы двух слагаемых вычесть одно слагаемое? если к вычитаемому прибавить разность? если из уменьшаемого вычесть разность?
Ответ:Получится число, равное другому слагаемому. Получится уменьшаемое. Получится вычитаемое.
Помни о названии компонентов действия сложения и вычитания:

А также – зависимости между компонентами и результатом действий сложения и вычитания.
1 слагаемое + 2 слагаемое = значение суммы.
Значение суммы – 1 слагаемое = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Если из суммы двух слагаемых вычесть одно слагаемое.
(а + в) – а = в + (а – а) = в – получится второе слагаемое.
Если к вычитаемому прибавить разность.
а – в = с, где а – уменьшаемое, в – вычитаемое, а с – разность, значит, с + в = а – получится уменьшаемое.
Если из уменьшаемого вычесть разность.
а – в = с, где а – уменьшаемое, в – вычитаемое, а с – разность, значит, а – с = в – получится вычитаемое.
Номер 5.
Как можно проверить сложение? вычитание?
Ответ:Из суммы вычесть одно из слагаемых. К разности прибавить вычитаемое или из уменьшаемого отнять разность.
Помни о названии компонентов действия сложения и вычитания:

А также – зависимости между компонентами и результатом действий сложения и вычитания.
Проверка сложения.
1 слагаемое + 2 слагаемое = значение суммы.
Проверка:
Значение суммы – 1 слагаемое = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Проверка вычитания.
Уменьшаемое – вычитаемое = значение разности.
Проверка:
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Номер 6.
Какие ты знаешь правила о порядке выполнения действий в выражениях без скобок? в выражениях со скобками?
Ответ:Сначала выполняются умножение и деление, а затем сложение и вычитание. Сначала выполняются действия в скобках.
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выражения в скобках и без скобок.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Оформляем задание в тетрадь.
Номер 22.
Дополни задачу недостающими данными и реши её. Из неисправного водопроводного крана в секунду капают 2 капли, а за 12 мин наполняется 1 полный стакан. Сколько литров воды может зря вылиться из такого крана в течение часа? в течение суток? (Считать в литре ☐ стаканов.)
Ответ:Считать, что в 1 литре 5 стаканов, потому что в одном стакане 200 мл.
Сколько стаканов воды выльется за 1 час?
60 : 12 = 5 (ст.) – за 1 час и это 1 л.
Значит за 1 час выливается 1 литр воды. За сутки (24 с) выльется 24 литра.
Ответ: 1 л воды выльется из крана за 1 час и 24 л воды выльется из крана за 1 сутки.
Номер 23.
Какую площадь занимает картофельное поле, если одна пятая часть этой площади составляет 200 м2?
Ответ:Все поле – ? м2.
1/5 часть – 200 м2.
200 ∙ 5 = 1000 (м2).
Ответ: 1000 м2 занимает картофельное поле.
Номер 24.
Какие числа пропущены в таблице?
Ответ:1 см2 = 100 мм2 1 м2 = 100 дм2 1 дм2 = 100 см2 1 км2 = 1000000 м2
Номер 25.
Запиши вычисления столбиком.
Ответ:45 км 530 м + 37 км 470 м = 83 км. 45 км 530 м = 45530 м. 37 км 470 м = 37470 м. 83000 м = 83 км.
24 км 040 м – 9 км 008 м = 15 км 032 м. 24 км 040 м = 24040 м. 9 км 008 м = 9008 м. 15032 м = 15 км 032 м.
32 т 820 кг – 8 т 950 кг = 23 т 870 кг. 32 т 820 кг = 32820 кг. 8 т 950 кг = 8950 кг. 23 т 870 кг = 23870 кг.
3 ч 15 мин – 45 мин = 2 ч 30 мин. 3 ч 15 мин = 195 мин. 195 мин − 45 мин = 150 мин. 150 мин = 2 ч 30 мин.

Номер 26.
Из двух одинаковых квадратов составили прямоугольник со сторонами 3 см и 1 см 5 мм. Сделай к задаче чертёж. Вырази длины сторон прямоугольника в миллиметрах и вычисли периметр этого прямоугольника и каждого квадрата.
Ответ:
3 см = 30 мм.
1 см 5 мм – 15 мм.
Периметр прямоугольника: (30 + 15) ∙ 2 = 90 (мм).
Периметр квадрата: 15 ∙ 4 = 60 (мм).
Ответ: периметр прямоугольника – 9 см, периметр каждого квадрата – 6 см.
Номер 27.
Начерти такие фигуры в тетради. В фигуре 1 найди одну девятую долю и закрась четыре таких доли, а в фигуре 2 закрась семь шестнадцатых долей. Найди площадь незакрашенной части фигуры 1.
Ответ:
3 ∙ 3 = 9 см2.
9 – 4 = 5 см2.
Ответ: 5 см2 площадь незакрашенной части фигуры 1.
Номер 1.
Как называются числа и соответствующие выражения при сложении? вычитании?
Ответ:При сложении: первое слагаемое, второе слагаемое, сумма. При вычитании: уменьшаемое, вычитаемое, разность.
Номер 2.
Какие свойства сложения ты знаешь?
Ответ:• Переместительное свойство сложения — от перестановки мест слагаемых значение суммы не меняется a + b = b + a.
• Сочетательное свойство сложения — можно складывать слагаемые в любом порядке. Значение суммы от этого не поменяется (Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.) (a + b) + c = a + (b + c).
• Свойство нуля при сложении — если к числу прибавить 0, получится тоже самое число. a + 0 = 0 + a = a.
Номер 3.
Что получится, если из суммы двух слагаемых вычесть одно слагаемое? если к вычитаемому прибавить разность? если из уменьшаемого вычесть разность?
Ответ:Если из суммы двух слагаемых вычесть одно слагаемое, то получится другое слагаемое. Если к вычитаемому прибавить разность, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое.
Номер 4.
Какие ты знаешь правила о порядке выполнения действий в выражениях без скобок? в выражениях со скобками?
Ответ:Сначала выполняются умножение и деление, а затем сложение и вычитание слева направо. Сначала находят значения выражений в скобках, а затем выполняют действия, как без скобок.
Номер 5.
Как можно проверить сложение? вычитание?
Ответ:Из суммы вычесть одно из слагаемых. К разности прибавить вычитаемое или из уменьшаемого отнять разность.
Номер 6.
Чему равна сумма двух слагаемых, если одно из них равно нулю? разность, если вычитаемое равно нулю?
Ответ:Сумма равна слагаемому неравному нулю. Разность равна уменьшаемому.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.