Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 30

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 143.
Прочитай числа, записанные в таблице.

Один миллион девятьсот девяносто девять тысяч четыреста девяносто. Сорок шесть миллионов. Девятьсот девяносто девять миллионов пятьсот тысяч. Четыреста миллиардов.
Помним о том, как читать числа:
1) Разбей число на классы, отсчитывая справа по 3 цифры.
2) Читай, сколько в числе единиц каждого класса, начиная с высшего, не произнося название класса единиц.
Анализируем числа в таблице.
1 999 499 – 1 единица класса миллионов, 999 единиц класса тысяч и 490 единиц класса единиц – один миллион девятьсот девяносто девять четыреста девяносто.
46 000 000 – 46 единиц класса миллионов, 0 единиц класса тысяч и 0 единиц класса единиц: сорок шесть миллионов.
999 500 000 – 999 единиц класса миллионов, 500 единиц класса тысяч и 0 единиц класса единиц – девятьсот девяносто девять тысяч пятьсот.
400 000 000 000 – 400 единиц класса миллиардов, 0 единиц класса миллионов, 0 единиц класса тысяч и 0 единиц класса единиц.
Читаем числа по плану.
1 999 499 – Один миллион девятьсот девяносто девять тысяч четыреста девяносто.
46 000 000 – Сорок шесть миллионов.
999 500 000 – Девятьсот девяносто девять миллионов пятьсот тысяч.
400 000 000 000 – Четыреста миллиардов.
Номер 144.
Объясни вычисления.

288:5
Делю сотни: сотен 2, но 2 сотни нельзя разделить на 5 так, чтобы в частном получились сотни.
Делю десятки: 2 сотни и 8 десятков — это 28 десятка.
Разделю 28 на 5. В частном будет 5 дес.
Умножаю 5 ∙ 5 = 25 дес.
Вычитаю 28 − 25 = 3. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 5; можно продолжать деление.
Делю единицы: 3 дес. и 8 ед. — это 38 единиц.
Делю 38 на 5. В частном будет 7 единиц.
Умножаю 7 ∙ 5 = 35.
Вычитаю 38 − 35 = 3. Сравниваю остаток с делителем: число оставшихся единиц меньше, чем 5. Деление закончено.
Ответ: 57 остаток 3.
(МОЖНО ПРОЩЕ: Попробуем по 5. Пять умножить на 5 = 25. 28 − 25 равно 3. Сносим 8. 38 нацело на 5 не делится. Попробуем взять число меньше. Это число 35, а 35 = 5 ∙ 7, значит попробуем по 7. 38 − 35 = 3. Следовательно, ответ: 57 и остаток 3.)
Проверять нужно так по правилам:
1 правило: при делении остаток всегда должен быть меньше делителя.
2 правило: чтобы найти делимое, зная делитель, остаток и неполное частное, нужно делитель умножить на неполное частное и прибавить остаток.
183 : 9
Делю сотни: сотен 1, но 1 сотню нельзя разделить на 9 так, чтобы в частном получились сотни.
Делю десятки: 1 сотня и 8 десятков — это 18 десятков.
Разделю 18 на 9. В частном будет 2 дес.
Умножаю 2 ∙ 9 = 18 дес.
Вычитаю 18 − 18 = 0.
Делю единицы:
Делю 3 на 9. В частном будет 0 единиц.
Умножаю 0 ∙ 9 = 0.
Вычитаю 3 − 0 = 3. Сравниваю остаток с делителем: число оставшихся единиц меньше, чем 9. Деление закончено.
Ответ: 20 остаток 3.
(МОЖНО ПРОЩЕ: Попробуем по 2. Два умножить на 9 будет 18. 18 − 18 ноль. Сносим 3. Три нацело на 9 не делится, значит, количество единиц в неполном частном — 0. Получили ответ 20 (остаток 3).)
Проверим по правилам:
1 правило: при делении остаток всегда должен быть меньше делителя.
2 правило: чтобы найти делимое, зная делитель, остаток и неполное частное, нужно делитель умножить на неполное частное и прибавить остаток.
Помним о том, что существует алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Проверяем по правилам:
1) При делении остаток всегда должен быть меньше делителя.
2) Чтобы найти делимое, зная делитель, остаток и неполное частное, нужно делитель умножить на неполное частное и прибавить остаток.
Выполняем письменное деление.
Выполним деление для того чтобы объяснить деление.
288 : 5
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 28 дес., потому что 2 сотни на 5 не делится. Высший разряд десятки, значит, в частном 2 знака.
2) Нахожу, количество десятков в частном: 28 дес. : 5 = 5 дес.
3) Нахожу, сколько десятков разделили: 5 дес. · 5 = 25 дес.
4) Нахожу, сколько десятков осталось разделить: 28 дес. – 25 дес. = 3 дес., 3 дес. < 5, значит, в частном 5 десятков.
5) Образую второе неполное делимое: 3 дес. – это 30 единиц да еще 8 единиц – 38 ед.
6) Нахожу количество единиц в частном: 38 ед. : 5 = 7 ед.
7) Нахожу, сколько единиц разделили: 7 ед. · 5 = 35 ед.
8) Нахожу, сколько единиц осталось разделить: 38 ед. – 35 ед. = 3 ед., 3 ед. < 5, значит, в частном – 7 единиц.
9) Деление окончено. Читаю ответ. Значение частного от деления 288 на 5 равно 57, остаток – 3.
183 : 9
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 18 дес., потому что 1 сотня на 9 не делится. Высший разряд десятки, значит, в частном 2 знака.
2) Нахожу, количество десятков в частном: 18 дес. : 9 = 2 дес.
3) Нахожу, сколько десятков разделили: 2 дес. · 9 = 18 дес.
4) Нахожу, сколько десятков осталось разделить: 18 дес. – 18 дес. = 0 дес., 0 дес. < 9, значит, в частном 2 десятка.
5) Образую второе неполное делимое: 0 дес. – это 0 единиц да еще 3 единицы – 3 ед.
6) Нахожу количество единиц в частном: 3 ед. : 9 = 0 ед.
7) Нахожу, сколько единиц разделили: 0 ед. · 9 = 0 ед.
8) Нахожу, сколько единиц осталось разделить: 3 ед. – 0 ед. = 3 ед., 3 ед. < 9, значит, в частном – 0 единиц.
9) Деление окончено. Читаю ответ. Значение частного от деления 183 на 9 равно 20, остаток 3.
Запишем числа в таблицу.

Номер 145.
Выполни деление с остатком и сделай проверку:
Ответ:
Помним о том, что существует алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Вспомни зависимость между компонентами и результатом действия умножения, деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного · делитель = делимое.
Вспомним.
Самопроверкой в ходе и результате вычислений является то, что:
1) Мы постоянно сравниваем остаток с делителем. Он всегда должен быть меньше делителя. В противном случае деление выполнении неверно или не завершено;
2) Мы проверяем, правильно ли подобрана цифра того или иного разряда через умножение на делитель. Цифра единиц разряда подобрана верно тогда, когда число от умножения меньше чем неполное делимое.
3) Мы получаем искомое число, выполняя умножения результата деления на делитель и прибавления остатка. Если число и делимое совпали, то деление выполнено верно. В противном случае, была допущена ошибка.
Выполняем деление и проверку.
Пишу: 611 : 7.
Делю сотни: 6 сотен нельзя разделить на 7 так, чтобы в частном получились сотни.
Делю десятки: 6 сот. и 1 дес. – это 61 дес.
Разделю 61 на 7. В частном будет 8 дес.
Умножу: 8 · 7 = 56. Разделили 56 дес.
Вычту: 61 - 56 = 5. Осталось разделить 5 дес.
Сравню остаток с делителем: число оставшихся десятков меньше, чем 7; можно продолжать деление.
Делю единицы: 5 дес. и 1 ед. – это 51 ед.
Разделю 51 на 7. В частном будет 7 ед.
Умножу: 7 · 7 = 49. Разделили 49 ед.
Вычту: 51 – 49 = 2. Остаток 2 ед.
Читаю ответ: 87 (ост. 2).
Пишу: 792 : 6.
Делю сотни: сотен 7.
Разделю 7 на 6. В частном будет 1 сот.
Умножу: 1 · 6 = 6. Разделили 6 сот.
Вычту: 7 – 6 = 1. Осталось разделить 1 сот.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 6; можно продолжать деление.
Делю десятки: 1 сот. и 9 дес. – это 19 дес.
Разделю 19 на 6. В частном будет 3 дес.
Умножу: 3 · 6 = 18. Разделили 18 дес.
Вычту: 19 – 18 = 1. Осталось разделить 1 дес.
Сравню остаток с делителем: число оставшихся десятков меньше, чем 6; можно продолжать деление.
Делю единицы: 1 дес. и 2 ед. – это 12 ед.
Разделю 12 на 6. В частном будет 2 ед.
Умножу: 2 · 6 = 12. Разделили 12 ед.
Вычту: 12 – 12 = 0. Единицы разделили все.
Читаю ответ: 132.
Пишу: 847 : 3.
Делю сотни: сотен 8.
Разделю 8 на 3. В частном будет 2 сот.
Умножу: 2 · 3 = 6. Разделили 6 сот.
Вычту: 8 – 6 = 2. Осталось разделить 2 сот.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 3; можно продолжать деление.
Делю десятки: 2 сот. и 4 дес. – это 24 дес.
Разделю 24 на 3. В частном будет 8 дес.
Умножу: 8 · 3 = 24. Разделили 24 дес.
Вычту: 24 – 24 = 0. Десятки разделили все.
Делю единицы: единиц 7.
Разделю 7 на 3. В частном будет 2 ед.
Умножу: 2 · 3 = 6. Разделили 6 ед.
Вычту: 7 – 6 = 1. Остаток 1 ед.
Читаю ответ: 282 (ост. 1).
Пишу: 968 : 9.
Делю сотни: сотен 9.
Разделю 9 на 9. В частном будет 1 сот.
Умножу: 1 · 9 = 9. Разделили 9 сот.
Вычту: 9 – 9 = 0. Сотни разделили все.
Делю десятки: 6 дес. нельзя разделить на 9 так, чтобы в частном получились десятки. Пишу в частном 0.
Умножу: 0 · 9 = 0. Разделили 0 дес.
Вычту: 6 – 0 = 6. Осталось разделить 6 дес.
Делю единицы: 6 дес. и 8 ед. – это 68 ед.
Разделю 68 на 9. В частном будет 7 ед.
Умножу: 7 · 9 = 63. Разделили 63 ед.
Вычту: 68 – 63 = 5. Осталось разделить 5 ед.
Читаю ответ: 107 (ост. 5).
Оформляем задание в тетрадь.

Номер 146.
Приготовленный из ягод сок разлили в банки. Получилось 15 банок, по 3 л в каждой, и еще осталось 2 л сока. Сколько литров сока приготовили?
Ответ:Разлили – 15 б. по 3 л
Осталось – 2 л
Всего – ? л
1) 3 ∙ 15 = 45 (л) – сока всего в банках.
2) 45 + 2 = 47 (л) – сока всего.
Ответ: 47 литров сока всего приготовили.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Объем 1 банки · количество банок = общее количество сока.
Общее количество сока : объем 1 банки = количество банок.
Общее количество сока : количество банок = объем 1 банки.
Оформляем условие в виде краткой записи или таблицы.
Разлили – 15 б. по 3 л.
Осталось – 2 л.
Всего – ? л.

Рассуждаем.
Общее количество сока складывается из количества сока в каждой банке, при этом объем 1 банки одинаковый. Значит, чтобы узнать, сколько всего сока разлили, нужно объем 1 банки умножаю на их количество.
1) 15 ∙ 3 = 45 (л) – сока всего в банках.
Продолжаем рассуждение.
Мы узнали, что было разлито 45 литров сока. При этом общее количество приготовленного сока складывается из количества разлитого сока и оставшегося. Значит, чтобы узнать, сколько сока приготовили, нужно сложить количество разлитого и оставшегося сока.
2) 45 + 2 = 47 (л) – сока всего.
Записываем ответ.
Ответ: 47 литров сока. Решение выражением: 3 · 15 + 2 = 47 (л).
Номер 147.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
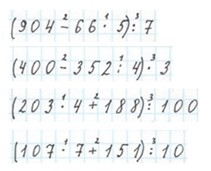
Выполняем вычисления.

Задание на полях страницы.
Магический квадрат.


Проверка: 12 + 19 + 14 = 19 + 26 = 45 17 + 15 + 13 = 30 + 15 = 45 16 + 11 + 18 = 16 + 29 = 45 12 + 17 + 16 = 29 + 16 = 45 19 + 15 + 11 = 30 + 15 = 45 14 + 13 + 18 = 27 + 18 = 45 12 + 15 + 18 = 30 + 15 = 45 16 + 15 + 14 = 15 + 30 = 45
Магический квадрат – квадрат, в котором числа по горизонтали, вертикали и диагонали в сумме дают одно и то же число.
Вычисление значений выражения сводится к применению правила:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Выполняем вычисления.
12 + 19 + 14 = 26 + 19 = 26 + (15 + 4) = (26 + 4) + 15 = 30 + 15 = 45
17 + 15 + 13 = 30 + 15 = 30 + (10 + 5) = (30 + 10) + 5 = 40 + 5 = 45
16 + 11 + 18 = 27 + 18 = 27 + (13 + 5) = (27 + 13) + 5 = 40 + 5 = 45
12 + 17 + 16 = 29 + 16 = 29 + (11 + 5) = (29 + 11) + 5 = 40 + 5 = 45
19 + 15 + 11 = 30 + 15 = 30 + (10 + 5) = (30 + 10) + 5 = 40 + 5 = 45
14 + 13 + 18 = 27 + 18 = 27 + (13 + 5) = (27 + 13) + 5 = 40 + 5 = 45
12 + 15 + 18 = 30 + 15 = 30 + (10 + 5) = (30 + 10) + 5 = 40 + 5 = 45
16 + 15 + 14 = 30 + 15 = 30 + (10 + 5) = (30 + 10) + 5 = 40 + 5 = 45
Оформляем задание в тетрадь.

Задание внизу страницы
Номер 147.
Прочитай числа, записанные в таблице.

Один миллион девятьсот девяносто девять тысяч четыреста девяносто. Сорок шесть миллионов. Девятьсот девяносто девять миллионов пятьсот тысяч. Четыреста миллиардов.
Номер 148.
Объясни вычисления.

288:5
Делю сотни: сотен 2, но 2 сотни нельзя разделить на 5 так, чтобы в частном получились сотни.
Делю десятки: 2 сотни и 8 десятков — это 28 десятка.
Разделю 28 на 5. В частном будет 5 дес.
Умножаю 5 ∙ 5 = 25 дес.
Вычитаю 28 − 25 = 3. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 5; можно продолжать деление.
Делю единицы: 3 дес. и 8 ед. — это 38 единиц.
Делю 38 на 5. В частном будет 7 единиц.
Умножаю 7 ∙ 5 = 35.
Вычитаю 38 − 35 = 3. Сравниваю остаток с делителем: число оставшихся единиц меньше, чем 5. Деление закончено.
Ответ: 57 остаток 3.
(МОЖНО ПРОЩЕ: Попробуем по 5. Пять умножить на 5 = 25. 28 − 25 равно 3. Сносим 8. 38 нацело на 5 не делится. Попробуем взять число меньше. Это число 35, а 35 = 5 ∙ 7, значит попробуем по 7. 38 − 35 = 3. Следовательно, ответ: 57 и остаток 3.)
Проверять нужно так по правилам:
1 правило: при делении остаток всегда должен быть меньше делителя.
2 правило: чтобы найти делимое, зная делитель, остаток и неполное частное, нужно делитель умножить на неполное частное и прибавить остаток.
183 : 9
Делю сотни: сотен 1, но 1 сотню нельзя разделить на 9 так, чтобы в частном получились сотни.
Делю десятки: 1 сотня и 8 десятков — это 18 десятков.
Разделю 18 на 9. В частном будет 2 дес.
Умножаю 2 ∙ 9 = 18 дес.
Вычитаю 18 − 18 = 0.
Делю единицы:
Делю 3 на 9. В частном будет 0 единиц.
Умножаю 0 ∙ 9 = 0.
Вычитаю 3 − 0 = 3. Сравниваю остаток с делителем: число оставшихся единиц меньше, чем 9. Деление закончено.
Ответ: 20 остаток 3.
(МОЖНО ПРОЩЕ: Попробуем по 2. Два умножить на 9 будет 18. 18 − 18 ноль. Сносим 3. Три нацело на 9 не делится, значит, количество единиц в неполном частном — 0. Получили ответ 20 (остаток 3).)
Проверим по правилам:
1 правило: при делении остаток всегда должен быть меньше делителя.
2 правило: чтобы найти делимое, зная делитель, остаток и неполное частное, нужно делитель умножить на неполное частное и прибавить остаток.
Номер 149.
Выполни деление с остатком и сделай проверку:
Ответ:
Номер 150.
Приготовленный из ягод сок разлили в банки. Получилось 15 банок, по 3 л в каждой, и еще осталось 2 л сока. Сколько литров сока приготовили?
Ответ:Разлили – 15 б. по 3 л
Осталось – 2 л
Всего – ? л
1) 15 ∙ 3 = 45 (л) – сока всего в банках.
2) 45 + 2 = 47 (л) – сока всего.
Ответ: 47 литров сока всего приготовили.
Номер 151.
Ответ:
Задание на полях страницы
Магический квадрат.


Проверка: 12 + 19 + 14 = 26 + 19 = 45 17 + 15 + 13 = 30 + 15 = 45 16 + 11 + 18 = 27 + 18 = 45 12 + 17 + 16 = 29 + 16 = 45 19 + 15 + 11 = 30 + 15 = 45 14 + 13 + 18 = 27 + 18 = 45 12 + 15 + 18 = 30 + 15 = 45 16 + 15 + 14 = 15 + 30 = 45
Задание внизу страницы
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.