Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 20

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Странички дя любознательных
Верно? Неверно?
Номер 1.
В числе 608 содержится 6 сотен и 8 десятков.
Ответ:Неверно 608 – 6 сотен и 8 единиц.
Помни о том, что каждая цифра в записи числа обозначает количество единиц определенного разряда.
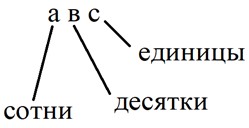
10 единиц низшего разряда образует 1 единицу высшего, т.е:
10 ед. = 1 дес.
10 дес. = 1 сот.
Проверим утверждение.
Запишем число 608 в таблицу

Получается, что в числе 608 не 6 сотен и 8 десятков, а 6 сотен и 8 единиц.
Делаем вывод.
Утверждение неверно.
Номер 2.
В одной тысяче содержится 10 сотен.
Ответ:Верно. 1тыс. = 1000 = 10 сот.
Помни о том, что 10 единиц низшего разряда образуют 1 единицу высшего.
Проверим утверждение.
Разряды следуют друг за другом в следующей последовательности:
Единицы – десятки – сотни – тысячи.
Значит, 10 ед. = 1 дес.
10 дес. = 1 сот.
10 сот. = 1 тыс.
Делаем вывод.
Утверждение верно.
Номер 3.
98 : 4 = 23 (ост. 6).
Ответ:Неверно. 98 : 4 = 24 (ост. 2).
Для того, чтобы доказать или опровергнуть данное равенство выполни действие или обратное ему.
Проверим утверждение.
Выполним действия:
98 : 4
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 9 дес. высший разряд – десятки, значит, в частном 2 знака.
2) Нахожу, количество десятков в частном: 9 дес. : 4 = 2 дес.
3) Нахожу, сколько десятков разделили: 2 дес. · 4 = 8 дес.
4) Нахожу, сколько десятков осталось разделить:
9 дес. – 8 дес. = 1 дес., 1 дес < 4, значит, в частном 2 десятка.
5) Образую второе неполное делимое: 1 дес. – это 10 ед. да еще 8 ед. – 18 ед.
6) Нахожу количество единиц в частном: 18 ед. : 4 = 4 ед.
7) Нахожу, сколько единиц разделили: 4 ед. · 4 = 16 ед.
8) Нахожу, сколько единиц осталось разделить:
18 ед. – 16 ед. = 2 ед., 2 ед. < 4, значит, в частном 4 единицы.
9) Читаю ответ. Значение частного от деления 98 на 4 равно 4. Остаток 2.
Делаем вывод.
Утверждение неверно.
Номер 4.
В частном чисел 864 и 9 будет две цифры.
Ответ:Верно. В частном будет 2 цифры, потому что будет 2 неполных делимых
Помним о том, что существует алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Проверим утверждение.
Следуя алгоритму, первым шагом мы выделяем первое неполное делимое. В данном делителе первое неполное делимое – 86 дес., потому что 8 сот. на 9 не поделишь.
Высший разряд – десятки, значит, в частном будет 2 знака, потому что десяток – двузначное число.
Делаем вывод.
Утверждение верно.
Номер 5.
36 ∙ 0 + 638 : 1 = 638.
Ответ:Верно. 36 · 0 + 638 : 1 = 0 + 638 = 638
Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо. Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Проверим утверждение.
36 ∙ 0 + 638 : 1 = 638
В данном равенстве отсутствуют скобки, поэтому действия выполняются умножение и деление, как они записаны слева направо, а затем – действие сложение.
1) 36 · 0 = 0, если любое число умножить на 0, то получится 0.
2) 638 : 1 = 638, если любое число разделить на 1, то получится это же число.
3) 0 + 638 = 638, если к 0 прибавить любое число, то получится тоже число.
Делаем вывод.
Утверждение верно.
Номер 6.
Высказывание «Сумму чисел 45 и 5 увеличить в 3 раза» можно записать так: 45 + 5 ∙ 3.
Ответ:Неверно. «Сумму чисел 45 и 5 увеличить в 3 раза» : (45 + 5) · 3
Сложение – слагаемое – сумма – знак плюс.
Умножение – умножить – значение произведения.
Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Проверим утверждение.
Высказывание.
Сумму чисел 45 и 5 увеличить в 3 раза» можно записать так: 45 + 5 ∙ 3.
Составим равенство по указанию.
(45 + 5) – 1 действие.
· 3 – 2 действие.
Получаем:
(45 + 5) ∙ 3
Делаем вывод.
Утверждение неверно.
Номер 7.
Егор сказал: «За 7 тетрадей я заплатил 28 р., а за 3 ластика – 18р. Значит, тетрадь дороже ластика».
Ответ:Неверно. 28 : 7 = 4 (р.) – стоит тетрадь; 18 : 3 = 6 (р.) – стоит ластик. Значит, тетрадь дешевле ластика.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Проверим утверждение.
Решим задачу.
Оформляем условие в виде таблицы.

Найдём стоимость 1 тетради и 1 ластика.
1) 28 : 7 = 4 (р.) – стоит тетрадь.
2) 18 : 3 = 6 (р.) – стоит ластик.
Сравним цены
4 < 6, т.е. тетрадь дешевле ластика.
Делаем вывод.
Утверждение верно.
Номер 8.
В выражении 70 − 27 : 9 + 9 ∙ 6 порядок действий указан правильно.
Ответ:Верно. Порядок указан верно: деление, умножение, вычитание, сложение
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Проверим утверждение.

В данном выражении отсутствуют скобки, но есть знаки арифметических действий разного уровня.
Поэтому сначала выполняются действия более высокого уровня: деление и умножения слева направо, как записаны. А потом действия более низкого уровня: вычитание и сложение слева направо, как записаны.
Делаем вывод.
Утверждение верно.
Номер 9.
Задача «Первая серия фильма продолжалась 40 мин, а последняя в 2 раза меньше. Сколько минут продолжалась последняя серия фильма?» решается сложением.
Ответ:Неверно 40 : 2 = 20 минут – длительность последней серии. Вывод: решается делением
«в 2 раза меньше», значит, вычисляется делением.
Проверим утверждение.
Решим задачу:

Первая серия фильма длится 40 минут, а последняя – в 2 раза меньше. Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, сколько длилась последняя серия, нужно длительность первой серии разделить на 2.
Вычисляется делением.
40 : 2 = 20 (мин.) – длилась вторая серия.
Делаем вывод.
Утверждение неверно.
Номер 10.
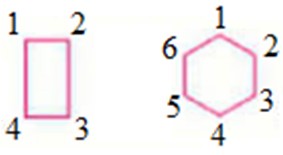
Фигуры отличаются друг от друга числом углов.

Верно в первой фигуре 4 угла, а во второй 6.
Помни, что фигуры называют по количество углов. 3 угла – треугольник, 4 угла – четырехугольник и т.д..
Проверим утверждение.
У первой фигуры 4 угла – четырёхугольник.
У ворой фигуры 6 углов – шестиугольник.
Делаем вывод.
Утверждение верно.
Номер 11.
Если периметр прямоугольника равен 24 см, то длина одной из его сторон может быть равна 14 см.
Ответ:Неверно (9 + 3) ∙ 2 = 24 см или (8 + 4) ∙ 2 = 24 см или (7 + 5) ∙ 2 = 24 см.
Периметр прямоугольника – сумма длин всех сторон. Чтобы вычислить периметр прямоугольника, нужно сложить длины всех сторон фигуры.
Проверим утверждение.
Используем метод перебора.
(9 + 3) ∙ 2 = 24 см.
(8 + 4) ∙ 2 = 24 см.
(7 + 5) ∙ 2 = 24 см.
Ни в одном из случаев нет стороны равной 14 см.
Предположим, что есть, тогда (14 + 1) · 2 = 30 см > 24 см.
Делаем вывод.
Утверждение неверно.
Номер 12.
Площадь прямоугольника со сторонами 18 см и 5 см можно вычислить так: 18 ∙ 5.
Ответ:Верно. Площадь прямоугольника вычисляется так: S = a · b, значит, 18 · 5
Площадь фигуры – часть плоскости, занятая фигурой. Чтобы вычислить площадь прямоугольника, нужно длину стороны умножить на ширину. Вычисляется умножением.
Проверим утверждение.
Для того чтобы проверить утверждение достаточно вспомнить , как находится площадь прямоугольника. Площадь прямоугольника находим умножением длины на ширину.
Длина – 18 см.
Ширина – 5 см.
S = 18 ∙ 5.
Делаем вывод.
Утверждение верно.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.