Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 78

Учебник 2 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 2.
Год: 2021-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Математика 2 часть. 3 класс - Учебник. Моро. Страница 78. Год 2024

Номер 10.

К весеннему севу надо отремонтировать 80 тракторов и 50 автомашин. В январе прошли ремонт 36 тракторов и 28 автомашин, в феврале – 40 тракторов и 21 автомашина. Объясни, что означают выражения.

Ответ:

36 + 40 = 76 (т.) – отремонтировали за 2 месяца. 28 + 21 = 49 (ав.) – отремонтировали за 2 месяца. 80 – 36 = 44 (т.) – осталось отремонтировать после января. 50 – 28 = 22 (ав.) – отремонтировать осталось после января. 80 – 36 – 40 = 4 (т.) – осталось отремонтировать. (36 + 28) − (40 + 21) = 3 (р.) – на столько отремонтировали тракторов больше, чем автомашин.

Подсказка:

1) Помни, что равенство – числовое выражение, составленное из чисел, знаков арифметических действий, скобок и знака равно.

2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Если к количеству тракторов, отремонтированных в январе, прибавить количество тракторов, отремонтированных в феврале, то узнаем сколько всего тракторов отремонтировали за 2 месяца.

36 + 40 = 76 (тракт.) – отремонтировали за 2 месяца.

Шаг 3.
Продолжаем рассуждение.

Если к количеству автомашин, отремонтированных в январе, прибавить количество автомашин, отремонтированных в феврале, то узнаем сколько всего автомашин отремонтировали за 2 месяца.

28 + 21 = 49 (автомаш.) – отремонтировали за 2 месяца.

Шаг 4.
Продолжаем рассуждение.

Если из общего количества отремонтированных тракторов вычесть количество тракторов, отремонтированных в январе, то узнаем сколько осталось отремонтировать тракторов после января.

80 − 36 = 44 (тракт.) – осталось отремонтировать после января.

Шаг 5.
Продолжаем рассуждение.

Если из общего количества отремонтированных автомашин вычесть количество автомашин, отремонтированных в январе, то узнаем сколько осталось отремонтировать автомашин после января.

50 − 28 = 22 (автомаш.) – осталось отремонтировать после января.

Шаг 6.
Продолжаем рассуждение.

Если общего количества тракторов вычесть поочередно количество тракторов, отремонтированных за январь и февраль, то узнаем сколько осталось отремонтировать тракторов.

80 − 36 − 40 = 44 − 4 = 4 (тракт.) – осталось отремонтировать.

Шаг 7.
Продолжаем рассуждение.

Если из общего количества отремонтированной техники в январе вычесть общее количество отремонтированной техники в феврале, то узнаем на сколько больше отремонтировали техники в январе, чем в феврале.

(36 + 28) − (40 + 21) = 3 (техники) – на столько больше отремонтировали в январе, чем в феврале.

1) 36 + 28 = 64
2) 40 + 21 = 61
3) 64 − 61 = 3

Шаг 8.
Оформляем задание в тетрадь.

36 + 40 = 76 (тракт.) – отремонтировали за 2 месяца.

28 + 21 = 49 (автомаш.) – отремонтировали за 2 месяца.

80 − 36 = 44 (тракт.) – осталось отремонтировать после января.

50 − 28 = 22 (автомаш.) – осталось отремонтировать после января.

80 − 36 − 40 = 4 (тракт.) – осталось отремонтировать.

(36 + 28) − (40 + 21) = 3 (техники) – на столько больше отремонтировали в январе, чем в феврале.

Номер 11.

В авторемонтной мастерской 90 рабочих: 72 слесаря, механиков в 6 раз меньше, чем слесарей, остальные электрики. Сколько ...?

Ответ:

Математика 2 часть. 3 класс - Учебник. Моро. Страница 78. Номер 11. Год 2024

1-й способ решения: 1) 72 : 6 = 12 (чел.) – механиков работало в автомастерской. 2) 72 + 12 = 84 (чел.) – слесаря и механика работало в автомастерской. 3) 90 – 84 = 6 (чел.) – электриков работало в автомастерской.
Ответ: 6 человек электриков работало в авторемонтной мастерской.
2-й способ решения: 1) 72 : 6 = (60 + 12 ) : 6 = 10 + 2 = 12 (чел.) – механики 2) 90 – 72 = 18 (чел.) – механики и электрики вместе 3) 18 – 12 = 6 (чел.) – электрики
Ответ: 6 электриков
3-й способ решения: 1) 72 : 6 = (60 + 12 ) : 6 = 10 + 2 = 12 (чел.) – механики 2) 90 – 12 = 78 (чел.) – слесари и электрики вместе 3) 78 – 72 = 6 (чел.) – электрики
Ответ: 6 электриков

Подсказка:

1) «В 6 раза меньше», значит, разделить на 6, т.е. вычисляется делением.

2) Вопрос к задаче: «Сколько в автомастерской работает электриков?»

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
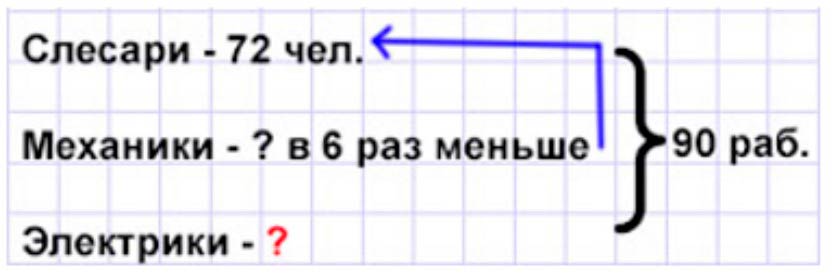
Рассуждаем.

По условию задачи механиков в 6 раз меньше, чем слесарей, значит количество слесарей разделили поровну на 6 частей и взяли одну такую часть. Соответственно, нужно 72 разделить на 6.

72 : 6 = (60 + 12 ) : 6 = 10 + 2 = 12 (чел.) – механики.

Шаг 3.
Продолжаем рассуждение.

Узнаем общее количество слесарей и механиков. Для этого сложим их значения.

72 + 12 = 84 (чел.) – слесари и механики вместе.

Шаг 4.
Продолжаем рассуждение.

Чтобы узнать сколько электриков в автомастерской нужно из общего количества ремонтников вычесть общее количество слесарей и механиков.

90 – 84 = 6 (чел.) – электрики.

Шаг 5.
Записываем ответ.

Ответ: 6 электриков.

Решение выражением:
90 – (72 + 72 : 6) = 90 – (72 + 12) = 90 – 84 = 6 (чел.) – электриков, где
72 : 6 – количество механиков;
72 + 72 : 6 – общее количество слесарей и механиков.

Номер 12.

Запиши выражения и вычисли их значения:

1) Сумму чисел 63 и 12 уменьшить в 3 раза. 2) Разность чисел 39 и 18 умножить на 4. 3) Из числа 750 вычесть частное чисел 12 и 3. 4) К числу 420 прибавить произведение чисел 9 и 6.

Ответ:

1) (63 + 12) : 3 = 25 2) (39 − 18) ∙ 4 = 84 3) 750 − (12 : 3) = 746 4) 420 + 9 ∙ 6 = 474

Подсказка:

1) сумма – это результат сложения;
2) разность – это результат вычитания;
3) частное – это результат деления;
4) произведение – это результат умножения.

Шаг 1.
Составим выражения.

Выражение 1.

1)
Сумма – это значит сложение, знак плюс.
63 + 12 – сумма чисел 63 и 12.

2)
Уменьшить в 3 раза – это значит разделить на 3, знак деления.
(63 + 12) : 3 – сумму чисел 63 и 12 уменьшить в 3 раза.

Выражение 2.

1)
Разность чисел – это вычитание, знак минус.
39 – 18 – разность чисел 39 и 18.

2)
Увеличить в 4 раза – это значит умножить на 4, знак умножить.
(39 − 18) ∙ 4 – разность чисел 39 и 18 умножить на 4.

Выражение 3.

1)
Частное – это значит деление.
12 : 3 – частное чисел 12 и 3.

2)
Из числа вычесть выражение – это значит вычитание, знак минус.
750 − 12 : 3 – из числа 750 вычесть частное чисел 12 и 3.

Выражение 4.

1)
Произведение – это значит умножение, знак умножить.
9 ∙ 6 – произведение чисел 9 и 6.

2)
К числу прибавить – это значит сложение, знак плюс.
420 + 9 ∙ 6 – к числу 420 прибавить произведение чисел 9 и 6.

Шаг 2.
Выполним вычисления по действиям.

1) (63 + 12) : 3 = 25
1) 63 + 12 = (60 + 10) + (3 + 2) = 70 + 5 = 75
2) 75 : 3 = (60 + 15) : 3 = 20 + 5 = 25

2) (39 − 18) ∙ 4 = 84
1) 39 – 18 = (30 – 10) + (9 – 8) = 20 + 1 = 21
2) 21 ∙ 4 = (20 + 1) ∙ 4 = 80 + 4 = 84

3) 750 − 12 : 3 = 746
1) 12 : 3 = 4
2) 750 – 4 = (740 + 10) – 4 = 740 + (10 – 4) = 740 + 6 = 746

4) 420 + 9 ∙ 6 = 474
1) 9 ∙ 6 = 54
2) 420 + 54 = 400 + (20 + 54) = 400 + 74 = 474

Шаг 3.
Оформим задание в тетрадь.

1)
Сумму чисел 63 и 12 уменьшить в 3 раза:
(63 + 12) : 3 = 75 : 3 = 25

2)
Разность чисел 39 и 18 умножить на 4:
(39 − 18) ∙ 4 = 21 ∙ 4 = 84

3)
Из числа 750 вычесть частное чисел 12 и 3:
750 − 12 : 3 = 750 – 4 = 746

4)
К числу 420 прибавить произведение чисел 9 и 6:
420 + 9 ∙ 6 = 420 + 54 = 474

Номер 13.

Выполни вычисления.

Ответ:

математика 3 класс учебник 2 часть Моро страница 78. Номер 13

17 ∙ 4 : 2 = 34 42 : 14 ∙ 26 = 78 28 ∙ 3 : 4 = 21 60 : 12 ∙ 14 = 70 18 ∙ 5 : 3 = 30 90 : 15 ∙ 13 = 78

Подсказка:

1) В 3 и 4 столбцах в выражения присутствуют только действия умножение и деление – они равноправны. Значит, выполняем действия по порядку слева направо.

2) Вспомни как складывает и вычитать по разрядам.

3) Помни, что разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.

Шаг 1.
Рассуждаем и выполняем вычисления.

Выполним вычисления в столбик.

Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 7 + 5 = 12
12 ед. – это 1 дес. и 2 ед.; 2 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 8 + 7 + 1 = 16
16 дес. – это 1 сот. 6 дес.; 6 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 1 + 1 = 2
Пишу под сотнями 2.
Ответ: 262.

Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы:
Из 3 ед. нельзя вычесть 6 ед. Беру 1 дес. из 5 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 5.)
1 дес. 0 ед. – это 10 ед.
10 − 6 = 4
Пишу под единицами 4.
Вычитаю десятки: Было 5 дес., но 1дес. взяли при вычитании единиц, поэтому осталось 4 дес.
Из 4 дес. нельзя вычесть 8 дес. Беру 1 сот. из 8 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 8.)
1 сот. 4 дес. – это 14 дес.
14 − 8 = 6
Пишу под десятками 6.
Вычитаю сотни: Было 8 сот., но 1 сот. взяли при вычитании десятков, поэтому осталось 7 сот.
Пишу под сотнями 7.
Читаю ответ: 764.

Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 8 + 3 = 11
11 ед. – это 1 дес. и 1 ед.; 1 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 3 + 9 + 1 = 13
13 дес.— это 1 сот. 3 дес.; 3 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 2 + 1 = 3
Пишу под сотнями 3.
Ответ: 331.

Вычислим по разрядам.

540 + 30 = 500 + (40 + 30) = 500 + 70 = 570

540 + 300 = (500 + 300) + 40 = 800 + 40 = 840

540 + 330 = (500 + 300) + (40 + 30) = 800 + 70 = 870

Выполним вычисления по действиям.

17 ∙ 4 : 2 = 34
1) 17 ∙ 4 = (10 + 7) ∙ 4 = 40 + 28 = 68
2) 68 : 2 = (60 + 8) : 2 = 30 + 4 = 34

28 ∙ 3 : 4 = 21
1) 28 ∙ 3 = (20 + 8) ∙ 3 = 60 + 24 = 84
2) 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21

18 ∙ 5 : 3 = 30
1) 18 ∙ 5 = (10 + 8) ∙ 5 = 50 + 40 = 90
2) 90 : 3 = 9 дес. : 3 = 3 дес. = 30

42 : 14 ∙ 26 = 78
1) 42 : 14 = 3
2) 3 ∙ 26 = 3 ∙ (20 + 6) = 60 + 18 = 78

60 : 12 ∙ 14 = 70
1) 60 : 12 = 5
2) 5 ∙ 14 = 5 ∙ (10 + 4) = 50 + 20 = 70

90 : 15 ∙ 13 = 78
1) 90 : 15 = 6
2) 6 ∙ 13 = 6 ∙ (10 + 3)= 60 + 18 = 78

Шаг 2.
Оформляем задание в тетрадь.

540 + 30 = 570
540 + 300 = 840
540 + 330 = 870

17 ∙ 4 : 2 = 68 : 2 = 34
28 ∙ 3 : 4 = 84 : 4 = 21
18 ∙ 5 : 3 = 90 : 3 = 30
42 : 14 ∙ 26 = 3 ∙ 26 = 78
60 : 12 ∙ 14 = 5 ∙ 14 = 70
90 : 15 ∙ 13 = 6 ∙ 13 = 78

Номер 14.

Отличается задание? Переключите год учебника.

2021 2024

Квадратный лист бумаги со стороной 2 дм разрезали на 5 равных частей прямоугольной формы. Найди площадь одной части. Реши задачу двумя способами.

Ответ:

1-й способ решения: 1) 20 : 5 = 4 (см) – ширина прямоугольника. 2) 4 ∙ 20 = 80 (см²) – площадь одной части.
Ответ: площадь одной части составляет 80 см².

2-й способ решения: 1) 20 ∙ 20 = 400 (см²) – площадь квадрата. 2) 400 : 5 = 80 (см²) – площадь одной части.
Ответ: площадь одной части составляет 80 см².

Подсказка:

1) Помни, что у квадрата все стороны равны.
2) Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
3) Доля – одна часть из тех, на которые разделили целое.
4) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
5) Вспомни, что 2 дм = 20 см.

Способ решения 1.

Шаг 1.
Оформляем условие в виде рисунка.

Квадрат можно нарисовать схематически, то есть с приблизительными значениями.

Шаг 2.
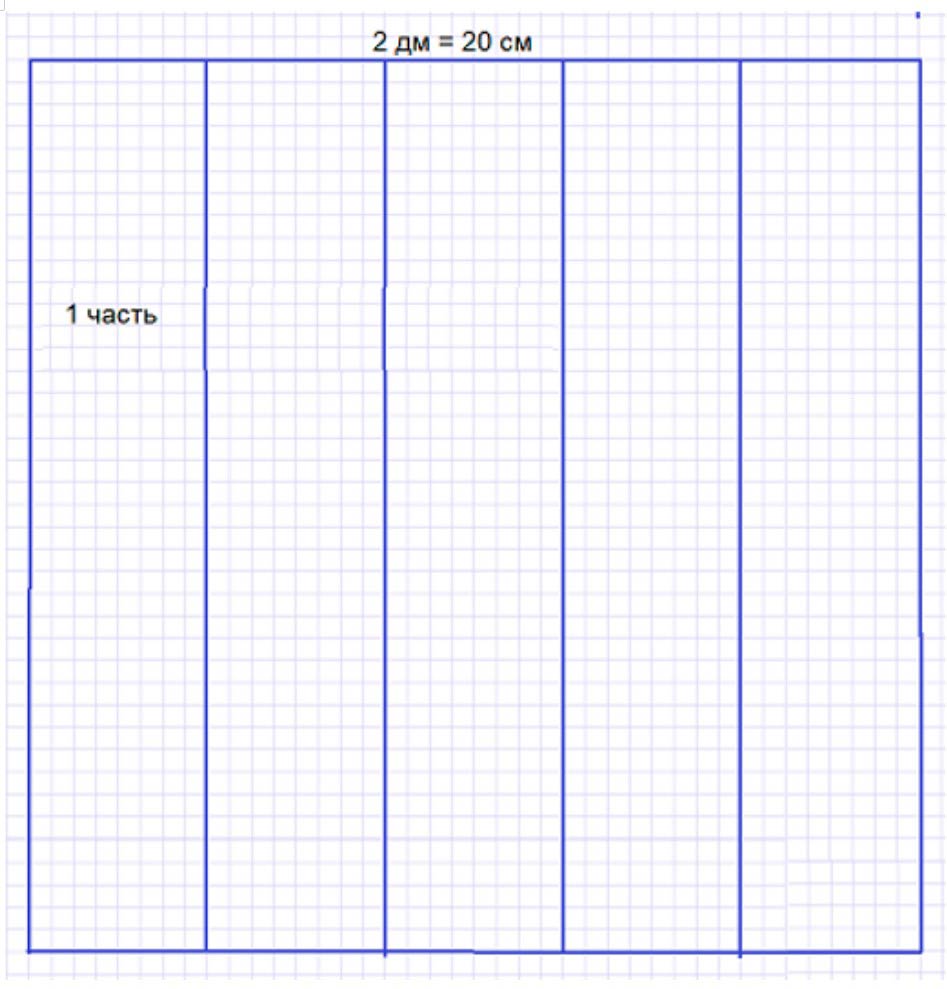
Рассуждаем.

Длина квадрата равна 2 дм = 20 см. Эту сторону разделим на 5 равных частей.
Значит, чтобы узнать длину пятой части квадрата, нужно строну квадрата разделить на 5.

20 : 5 = 4 (см) – одна пятая ширины квадрата.

Шаг 3.
Продолжаем рассуждение.

Длина одной пятой фигуры равна 4 см, а ширина совпадает с шириной квадрата, то есть ширина равна 20 см.
Чтобы найти площадь прямоугольника нужно длину умножить на ширину.

4 ∙ 20 = 80 (см²) – площадь одной части.

Шаг 4.
Записываем ответ.

Ответ: 80 см².

Решение выражением:
20 : 5 ∙ 20 = 80 (см²) – площадь одной пятой квадрата,
где 20 : 5 – одна пятая часть ширины квадрата.

Способ решения 2.

Шаг 1.
Рассуждаем.

Найдём площадь квадрата. Для этого умножим длину на ширину, но у квадрата длина равна ширине.

20 ∙ 20 = 400 (см²) – площадь квадрата.

Шаг 2.
Продолжаем рассуждение.

Квадрат разделили на 5 равных частей и нам нужно взять только одну такую часть. Значит, чтобы найти площадь одной пятой площади квадрата нужно площадь квадрата разделить на 5.

400 : 5 = 40 дес. : 5 = 8 дес. = 80 (см²) – площадь одной части.

Шаг 3.
Записываем ответ.

Ответ: 80 см².

Решение выражением:
20 ∙ 20 : 5 = 80 (см²) – площадь одной пятой части,
где 20 ∙ 20 – площадь квадрата.

Квадратный лист бумаги со стороной 2 дм разрезали на пять равных частей прямоугольной формы. Найди площадь одной части. Сколькими способами можно решить эту задачу? Какой способ выбираешь ты?

Ответ:

Подсказка:

Задачу можно решить двумя способами.

Способ решения 1.

Шаг 1.
Рассуждаем.

Длина квадрата равна 2 дм = 20 см. Квадрат разделили на 5 равных частей прямоугольной формы. Значит, чтобы узнать ширину прямоугольника, нужно строну квадрата разделить на 5.

20 : 5 = 4 (см) – ширина прямоугольника.

Шаг 2.
Продолжаем рассуждение.

Длина прямоугольника совпадает с длиной квадрата, то есть равна 20 см.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.

4 ∙ 20 = 80 (см²) – площадь одной части.

Шаг 3.
Записываем ответ.

Ответ: 80 см².

Способ решения 2.

Шаг 1.
Рассуждаем.

Шаг 2.
Продолжаем рассуждение.

Квадрат разделили на 5 равных частей, и нам нужно взять только одну такую часть. Значит, чтобы найти площадь одной пятой площади квадрата нужно площадь квадрата разделить на 5.

400 : 5 = 40 дес. : 5 = 8 дес. = 80 (см²) – площадь одной части.

Шаг 3.
Записываем ответ.

Ответ: 80 см².

Задание на полях страницы

Ответ:

Подсказка:

1) Вспомни как складывает и вычитать по разрядам.
2) Помни, что разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.

Рассмотрим первый ребус.

Шаг 1.
Рассуждаем.

Рассмотрим разряд единиц.
Количество единиц первого слагаемого неизвестно, но известно количество единиц второго слагаемого и количество единиц суммы.
Чтобы найти единицы первого слагаемого нужно из количества единиц суммы вычесть количество единиц второго слагаемого.
Вспомним, при сложении с каким числом число 6 образует 2 единицы. Это число 6, так как 6 + 6 = 12 – это 1 дес. и 2 ед.
6 единиц – во первом слагаемом.

Шаг 2.
Продолжаем рассуждение.

Рассмотрим разряд десятков.
Количество десятков второго слагаемого неизвестно, но известно количество десятков первого слагаемого и количество десятков суммы.
Чтоб найти десятки второго слагаемого нужно из количества единиц суммы вычесть количество единиц первого слагаемого.
Вспомни, что 1 ед. десятков ушла в десятки при сложении единиц, поэтому:
8 дес. + 1 дес. = 9 дес.
Вспомним, при сложении с каким числом число 9 образует 0 десятков. Это число 1, так как 9 + 1 = 10 – это 1 дес. и 0 ед.
1 десяток – во втором слагаемом.

Шаг 3.
Продолжаем рассуждение.

Рассмотрим разряд сотен.
Количество сотен суммы неизвестно, но известно количество сотен первого и второго слагаемого.
Чтобы найти сотни суммы, нужно количество сотен первого и второго слагаемых сложить.
Но помним, что 1 ед. сотен ушла в сотни при сложении десятков, поэтому:
2 + 3 + 1 = 6
6 сотен – в сумме.

Шаг 4.
Делаем проверку.

Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 6 + 6 = 12
12 ед. – это 1 дес. и 2 ед.; 2 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 8 + 1 + 1 = 10
10 дес.— это 1 сот. 0 дес.; 0 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 2 + 3 + 1 = 6
Пишу под сотнями 6.
Ответ: 602.

Шаг 5.
Оформляем задание в тетрадь.

Получаем равенство: 286 + 316 = 602

Рассмотрим второй ребус.

Шаг 1.
Рассуждаем.

Количество единиц уменьшаемого не известно, но известно количество единиц вычитаемого и единицы разности.
Чтобы найти единицы уменьшаемого, нужно сложить количество единиц вычитаемого и единицы разности.
7 ед. + 5 ед. = 12 ед.= 1 дес. 2 ед. – в уменьшаемом 2 единицы, а 1 дес. заняли у десяток.

2 единицы – в уменьшаемом.

Шаг 2.
Продолжаем рассуждение.

Количество десятков вычитаемого не известно, но известно количество десятков уменьшаемого и количество десятков разности.
Чтобы найти количество десятков вычитаемого, нужно из количества десятков уменьшаемого вычесть количество десятков разности.

2 дес. – 1 дес. = 2 дес. и ещё 1 дес. занимали для вычисления единиц, поэтому:
1 дес. – 1 дес. = 0 дес.

0 десяток – в вычитаемом.

Шаг 2.
Продолжаем рассуждение.

Количество сотен уменьшаемого не известно, но известно количество сотен вычитаемого и сотен разности.
Чтобы найти сотни уменьшаемого, нужно сложить количество сотен вычитаемого и разности.
8 сот. + 1 сот. = 9 сот.

9 сотен в уменьшаемом.

Шаг 3.
Делаем проверку.

Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы:
Из 2 ед. нельзя вычесть 7 ед. Беру 1 дес. из 2 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 2.)
1 дес. 2 ед. – это 12 ед.
12 – 7 = 5
Пишу под единицами 5.
Вычитаю десятки: Было 2 дес., но 1 дес. взяли при вычитании единиц, поэтому осталось 1 дес.
1 – 1 = 0
Пишу под десятками 0.
Вычитаю сотни: 9 – 1 = 8
Пишу под сотнями 8.
Читаю ответ: 805.

Шаг 4.
Оформляем задание в тетрадь.

Получаем равенство: 922 – 117 = 805