Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 52

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Номер 1.
Посмотри, как на циферблате числа записаны римскими цифрами: I (1), V (5), X (10). Запомни эти цифры. Обрати внимание, как с их помощью записаны числа: II (2) и III (3), IV (4) и VI (6), IX (9) и XI (11).

1 - I - один
2 - II - два
3 - III - три
4 - IV - четыре
5 - V - пять
6 - VI - шесть
7 - VII - семь
8 - VIII - восемь
9 - IX - девять
10 - X - десять
11 - XI - одиннадцать
12 - XII - двенадцать
Для выполнения задания нужно внимательно рассмотреть часы.
Рассуждаем.
Внимательно рассмотри часы и сопоставь римские цифры и арабские.
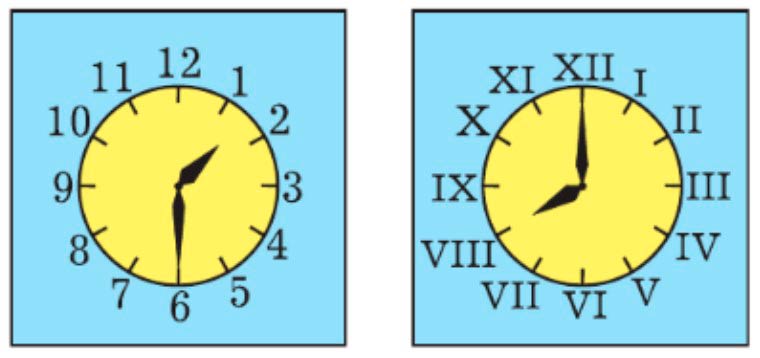
Для правильной записи римские цифры записывают так: если меньшая цифра стоит после большей цифры, то они складываются, если же меньшая цифра стоит перед большей, то из большей вычитаем меньшую цифру.
Важно запомнить главные числа: I = 1, V = 5, X = 10.
I = 1
II = 1 + 1 = 2
III = 1 + 1 + 1 = 3
IV = 5 – 1 = 4, так как 1 стоит перед 5
V = 5
VI = 5 + 1 = 6, так как 1 стоит перед 5
VII = 5 + 2 = 7, так как 5 стоит перед 2
VIII = 5 + 3 = 8, так как 5 стоит перед 3
IX = 10 – 1 = 9, так как 1 стоит перед 10
X = 10
XI = 10 + 1 = 11, так как 10 стоит перед 1
XII = 10 + 2 = 12, так как 10 стоит перед 2
Оформляем задание в тетрадь.
Выучи обозначение римских чисел:
I = 1
II = 2
III = 3
IV = 4
V = 5
VI = 6
VII = 7
VIII = 8
IX = 9
X = 10
XI = 11
XII = 12
Номер 2.
Ответ:III < V IX > VIII XII > VII VI > IV XI > IX IV < IX
Вспомни обозначение римских чисел.
Рассуждаем.
III < V , так как 3 < 5
VI > IV, так как 6 > 4
IX > VIII, так как 9 > 8
XI > IX, так как 11 > 9
XII > VII, так как 12 > 8
IV < IX, так как 4 < 9
Оформляем задание в тетрадь.
III < V
VI > IV
IX > VIII
XI > IX
XII > VII
IV < IX
Номер 3.
Заполни окошки.
Ответ:III + I = IV IV – II = II XII – III = IX IX + II = XI IV + III = VII III + III = VI
1) Вспомни обозначение римских чисел.
2) Помни, что I = 1, V = 5, X = 10.
Рассуждаем.
III + I = IV, так как 3 + 1 = 4
IX + II = XI, так как 9 + 2 = 11
IV − II = II, так как 4 − 2 = 2
IV + III = VII, так как 4 + 3 = 7
XII − III = IX, так как 12 − 3 = 9
III + III = VI, так как 3 + 3 = 6
Оформляем задание в тетрадь.
III + I = IV
IX + II = XI
IV − II = II
IV + III = VII
XII − III = IX
III + III = VI
Номер 4.
В выложенных из палочек равенствах с римскими цифрами допущены ошибки. Как надо переложить по одной палочке в каждом равенстве, чтобы исправить ошибку? Запиши верные равенства.

V + I = VI X + II = XII X - I = IX
1) Вспомни обозначение римских чисел.
2) Внимательно рассмотри выражения и составь верные равенства (примеры).
3) Помни, что I = 1, V = 5, X = 10.
Рассуждаем.
Рассмотрим первое выражения.
Если палочку у первого числа переставим к последнему числу, то получится верное равенство.
.jpg)
Продолжаем рассуждение.
Рассмотрим второе выражение.
Если палочку у второго числа переставим к последнему числу, то получим верное равенство.
.jpg)
Продолжаем рассуждение.
Рассмотрим третье выражение.
Если палочку у первого числа переместить вперед, так чтобы из IX получилось XI, то получится верное равенство.
.jpg)
Оформляем задание в тетрадь.
V + I = VI, так как 5 + 1 = 6
X + II = XII, так как 10 + 2 = 12
XI — I = X, так как 11 – 1 = 10
Номер 5.
Запиши с помощью римских цифр: сколько тебе лет; сколько тебе будет лет через 2 года; сколько тебе было лет 2 года тому назад.
Ответ:X лет; XII лет; VIII лет.
1) Вспомни обозначение римских чисел.
2) Помни, что I = 1, V = 5, X = 10.
Рассуждаем.
Выполни задание используя план:
1) Запиши свой возраст с помощью римских цифр;
2) К своему возрасту прибавь 2 года и переведи число с помощью римских цифр;
3) От своего возраста отними 2 года и переведи число с помощью римских цифр.
Продолжаем рассуждение.
Выбери вариант ответа, учитывая свой возраст:
1)
Если тебе 9 лет:
Возраст: IX – 9 лет
Возраст через 2 года: IX + II = XI, 9 + 2 = 11
Возраст 2 года назад: IX – II = VII, 9 – 2 = 7
2)
Если тебе 10 лет:
Возраст: X – 10 лет
Возраст через 2 года: X + II = XII, 10 + 2 = 12
Возраст 2 года назад: X – II = VIII, 10 – 2 = 8
3)
Если тебе 11 лет:
Возраст: XI – 11 лет
Возраст через 2 года: XI + II = XIII, 11 + 2 = 13
Возраст 2 года назад: XI – II = IX, 11 – 2 = 9
Оформляем задание в тетрадь.
Выбери вариант ответа, учитывая свой возраст:
1)
Если тебе 9 лет:
Возраст сейчас: IX
Возраст через 2 года: XI
Возраст 2 года назад: VII
2)
Если тебе 10 лет:
Возраст сейчас: X
Возраст через 2 года: XII
Возраст 2 года назад:VIII
3)
Если тебе 11 лет:
Возраст сейчас: 11 лет
Возраст через 2 года: XIII
Возраст 2 года назад: IX
Единицы массы. Грамм
Номер 1.
Какие гири надо взять, чтобы получить 7 г? 80 г? 300 г? 600 г? 745 г? 900 г?
Ответ:7 г = 2 г + 5 г 80 г = 50 г + 20 г + 10 г 300 г = 100 г + 200 г 600 г = 500 г + 100 г 745 г = 500 г + 200 г + 20 г + 20 г + 5 г 900 г = 500 г + 200 г + 200 г
Вспомни какие бывают гири:
1 кг 2 кг 5 кг
100 г 200 г 500 г
10 г 20 г 50 г
1 г 2 г 5 г
Рассуждаем.
С помощью гирь получим:
7 г можно получить двумя гирями – 5 г и 2 г.
7 г = 5 г + 2 г
80 г можно получить тремя гирями – 50 г, 20 г и 10 г.
80 г = 50 г + 20 г + 10 г
300 г можно получить двумя гирями – 200 г и 100 г.
300 г = 200 г + 100 г
600 г можно получить двумя гирями – 500 г и 100 г.
600 г = 500 г + 100 г
745 г можно получить 5 гирями – 500 г, 200 г, 20 г, 20 г и 5 г.
745 г = 500 г + 200 г + 20 г + 20 г + 5 г
900 г можно получить тремя гирями – 500 г, 200 г и 200 г.
900 г = 500 г + 200 г + 200 г
Оформляем задание в тетрадь.
7 г = 5 г + 2 г
80 г = 50 г + 20 г + 10 г
300 г = 200 г + 100 г
600 г = 500 г + 100 г
745 г = 500 г + 200 г + 20 г + 20 г + 5 г
900 г = 500 г + 200 г + 200 г
Номер 2.
Девочка купила 2 пачки печенья, по 200 г каждая, и 2 пачки чая, по 50 г каждая. Задай вопрос и реши задачу. Сколько вопросов можно задать к этому условию задачи?
Ответ:Вопрос: Какая масса всей покупки?

1) 200 ∙ 2 = 400 (г) – масса печенья
2) 50 ∙ 2 = 100 (г) – масса чая
3) 400 + 100 = 500 (г) – масса всей покупки.
Ответ: масса всей покупки составляет 500 г.
Другие вопросы:
1) Какова масса всего печенья?
Ответ: масса всего печенья составляет 400 г.
2) Какова масса всего чая?
Ответ: масса всего чая составляет 100 г.
3) На сколько масса всего печенья больше, чем масса всего чая?
Ответ: масса всего печенья на 300 г больше массы всего чая.
Данная задача: вида «Масса 1 предмета, количество предметов, общая масса» характеризуется зависимостями между элементами:
Масса 1 предмета · количество предметов = общая масса.
Общая масса : масса 1 предмета = количество предметов.
Общая масса : количество предметов = масса 1 предмета.
Оформляем условие в виде таблицы.
Вопрос задачи: Какова общая масса всей покупки?
.jpg)
Рассуждаем.
Масса пачки печенья – 200 г. Чтобы узнать, какова масса всех пачек печенья, нужно массу 1 пачки умножить на количество пачек.
200 ∙ 2 = 2 сот. ∙ 2 = 4 сот. = 400 (г) – масса 2 пачек печенья.
Продолжаем рассуждение.
Масса пачки чая – 50 г. Чтобы узнать, какова масса всех пачек чая, нужно массу 1 пачки умножить на количество пачек.
50 ∙ 2 = 5 дес. ∙ 2 = 10 дес. = 100 (г) – масса 2 пачек чая.
Продолжаем рассуждение.
Общая масса покупки складывается из общей массы печенья и чая. Значит, сложим эти массы.
400 + 100 = 500 (г) – масса всей покупки.
Записываем ответ.
Ответ: 500 грамм.
Продолжаем рассуждение.
Другие вопросы:
1) Какова масса всего печенья?
200 ∙ 2 = 400 (г) – масса всего печенья.
Ответ: масса всего печенья составляет 400 грамм.
2) Какова масса всего чая?
50 ∙ 2 = 100 (г) – масса всего чая.
Ответ: масса всего чая составляет 100 грамм.
3) На сколько масса всего печенья больше, чем масса всего чая?
400 – 100 = 300 (г) – на столько масса всего печенья больше массы всего чая.
Ответ: масса всего печенья на 300 грамм больше массы всего чая.
Номер 3.
Реши уравнения.
Ответ:100 + х = 200 х = 200 − 100 х = 100 Проверка: 100 + 100 = 200 200 = 200 Ответ: х = 100
х ∙ 140 = 140 х = 140 : 140 х = 1 Проверка: 1 * 140 = 140 140 = 140 Ответ: х = 1
390 – х = 90 х = 390 - 90 х = 300 Проверка: 390 - 300 = 90 90 = 90 Ответ: х = 300
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Решаем уравнения.
100 + х = 200
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
х = 200 – 100
х = 100
х ∙ 140 = 140
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведения разделить на известный множитель.
х = 140 : 140
Если число разделить само на себя, то получим 1.
х = 1
390 – х = 90
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 390 – 90
х = 300
Сделаем проверку.
100 + х = 200
Вместо неизвестного подставим число 100.
100 + 100 = 1 сот. + 1 сот. = 2 сот. = 200
200 = 200
х ∙ 140 = 140
Вместо неизвестного подставим число 1.
1 ∙ 140 = 140
Если любое число умножить на 1, то получим само число.
140 = 140
390 – х = 90
Вместо неизвестного подставим число 300.
390 – 300 = 300 + 90 – 300 = 90
90 = 90
Оформляем задание в тетрадь.
100 + х = 200
х = 200 – 100
х = 100
Проверка:
100 + 100 = 200
200 = 200
х ∙ 140 = 140
х = 140 : 140
х = 1
Проверка:
1 ∙ 140 = 140
140 = 140
390 – х = 90
х = 390 – 90
х = 300
Проверка:
390 – 300 = 90
90 = 90
Номер 4.
Ответ:328 – 20 = 308
406 – 6 = 400
320 : 10 – 170 : 10 = 15
(750 − 50) : 100 ∙ 1 = 7
1000 − (200 + 300) = 500
1000 − (480 − 80) = 600
1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Помни, что при умножении любого числа на 1 получается то число, которое умножили.
5) Чтобы разделить число на 100, нужно убрать у него справа два нуля.
Расставляем порядок действий и выполняем вычисления.
328 – 20 = 300 + 20 + 8 – 20 = 308
406 – 6 = 400 + 6 – 6 = 400
320 : 10 – 170 : 10 = 15
1) 320 : 10 = 32
2) 170 : 10 = 17
3) 32 – 17 = 15
(750 – 50) : 100 ∙ 1 = 7
1) 750 – 50 = 700 + 50 – 50 = 700
2) 700 : 100 = 7
3) 7 ∙ 1 = 7
1000 – (200 + 300) = 500
1) 200 + 300 = 2 сот. + 3 сот. = 5 сот. = 500
2) 1000 – 500 = 10 сот. – 5 сот. = 5 сот. = 500
1000 – (480 – 80) = 600
1) 480 – 80 = 400 + 80 – 80 = 400
2) 1000 – 400 = 10 сот. – 4 сот. = 6 сот. = 600
Оформляем задание в тетрадь.
328 – 20 = 308
406 – 6 = 400
320 : 10 – 170 : 10 = 32 – 17 = 15
(750 – 50) : 100 ∙ 1 = 700 : 100 ∙ 1 = 7
1000 – (200 + 300) = 1000 – 500 = 500
1000 – (480 – 80) = 1000 – 400 = 600
Номер 5.
Начерти в тетради любую фигуру, кроме прямоугольника, так, чтобы ее площадь была равна 12 см2.
Ответ:Чертим прямоугольник площадью в 24 см2, а затем проводим прямую, соединяющую две противоположные вершины. Половина прямоугольника-искомая фигура с площадью 12 см2.

1) 6 ∙ 4 = 24 (см2) 2) 24 : 2 = 12 (см2)
1) Чтобы найти площадь прямоугольника, нужно его длину умножит на ширину.
2) Диагональ прямоугольника делит фигуру на два равных треугольника.
Рассуждаем.
Чтобы начертить треугольник площадью 12 см2, нужно вначале начертить прямоугольник площадью в 2 раза больше данной, а потом разделить его пополам.
12 ∙ 2 = 24 (см2) – площадь прямоугольника, который нужно начертить.
Продолжаем рассуждение.
Число 24 можно представить в виде произведения чисел 6 и 4.
24 = 6 ∙ 4
Значит, стороны прямоугольника равны 6 см и 4 см.
Выполняем задание.
Начертим прямоугольник и разделим его пополам.
Половина прямоугольника площадью 24 см2 и есть фигура с площадью 12 см2.
.jpg)
Задание вверху страницы

Расмотри рисунок и скажи: масса кочана капусты больше или меньше чем 1 кг? Чем 2 кг?
Чтобы узнать точнее массу предметов, используют не только килограмм, но и более мелкую единтцу массы – грамм. В одном килограмме 1000 граммов.
Ответ:Масса кочана больше 1 кг, так как чаша весов где висит гиря ниже, чем гиря в 1 кг. Масса кочана меньше 2 кг, так как чаша весов где висит гиря выше, чем 2 гири по 1 кг. Значит, кочан капусты больше 1 кг, но меньше 2 кг.
Внимательно рассмотри рисунок и ответь на вопросы.
Рассуждаем.
Рассмотрим первые весы.
-(2024).jpg)
Чаша весов, где лежит кочан капусты, ниже чаши весов, на которой стоит гиря 1 кг. Значит, масса кочана капусты тяжелее 1 кг.
Продолжаем рассуждение.
Рассмотрим вторые весы.
-(2024).jpg)
Чаша весов, где лежит кочан капусты, выше чаши весов, на которой стоят 2 гири по 1 кг. Значит, масса кочана капусты легче, чем 2 кг.
Делаем вывод.
Масса кочана больше 1 кг, так как чаша весов где висит гиря ниже, чем гиря в 1 кг.
Масса кочана меньше 2 кг, так как чаша весов где висит гиря выше, чем 2 гири по 1 кг.
Значит, кочан капусты больше 1 кг, но меньше 2 кг.
Задание внизу страницы
Купили 3 пачки вафель, по 100 г каждая. Найди массу этой покупки.
Ответ:100 ∙ 3 = 300 (г) Ответ: 300 г масса покупки.
Чтобы умножить число на 100, нужно дописать у него справа два нуля.
Оформляем краткую запись.
Вафли – 3 пачки.
1 пачка – 100 гр
Вся покупка – ? гр
Рассуждаем.
Чтобы узнать, какова масса всех пачек вафель, нужно массу 1 пачки умножить на количество пачек.
100 ∙ 3 = 1 сот. ∙ 3 = 3 сот. = 300 (г) – общая масса вафель.
Записываем ответ.
Ответ: 300 грамм масса покупки.
Задание на полях страницы
Начерти. Проведи 2 оси симметрии. Раскрась.


Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
Начертим фигуру.
Начертим друг под другом 3 квадрата со стороной 3 клетки и расстоянием между ними 3 клетки.
Начиная с центра первого квадрата начерти друг под другом 5 квадратов со стороной 1 клетка и расстоянием 3 клетки.
Соедини отрезками углы больших квадратов и углы маленьких квадратов, которые лежат между больших квадратов.
-(2024).jpg)
Раскрасим фигуру.
Ось симметрии – это прямая линия, которая делит фигуру на две зеркально одинаковых фигуры. При сложении по данной линии фигуры совпадут.
В данной фигуре две оси симметрии – горизонтальная и вертикальная.
-(2024).jpg)
Красными линиями показаны оси симметрии.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.